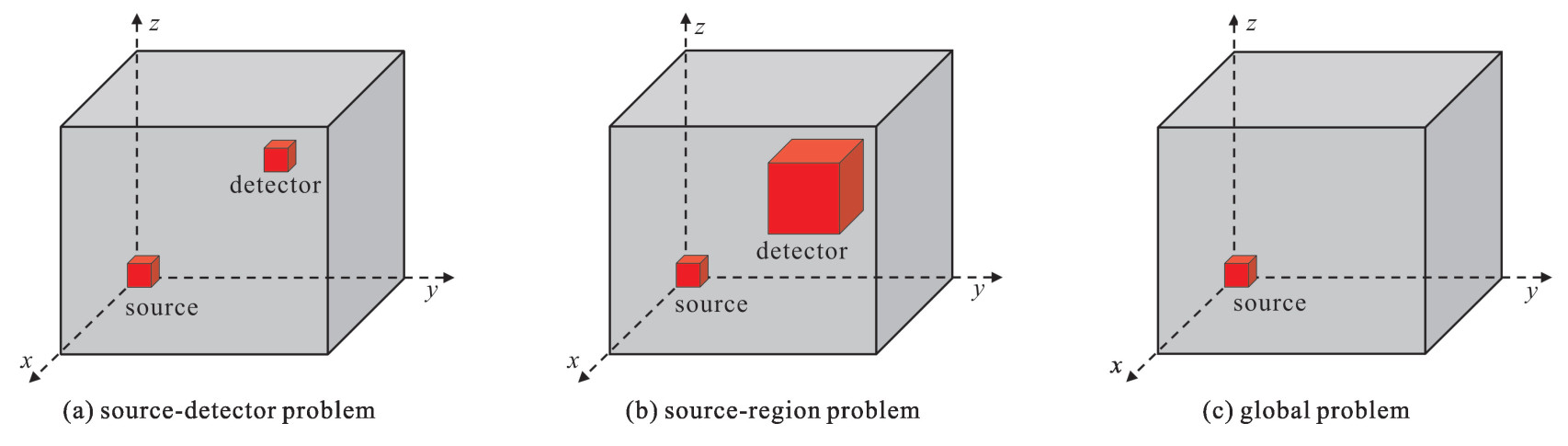
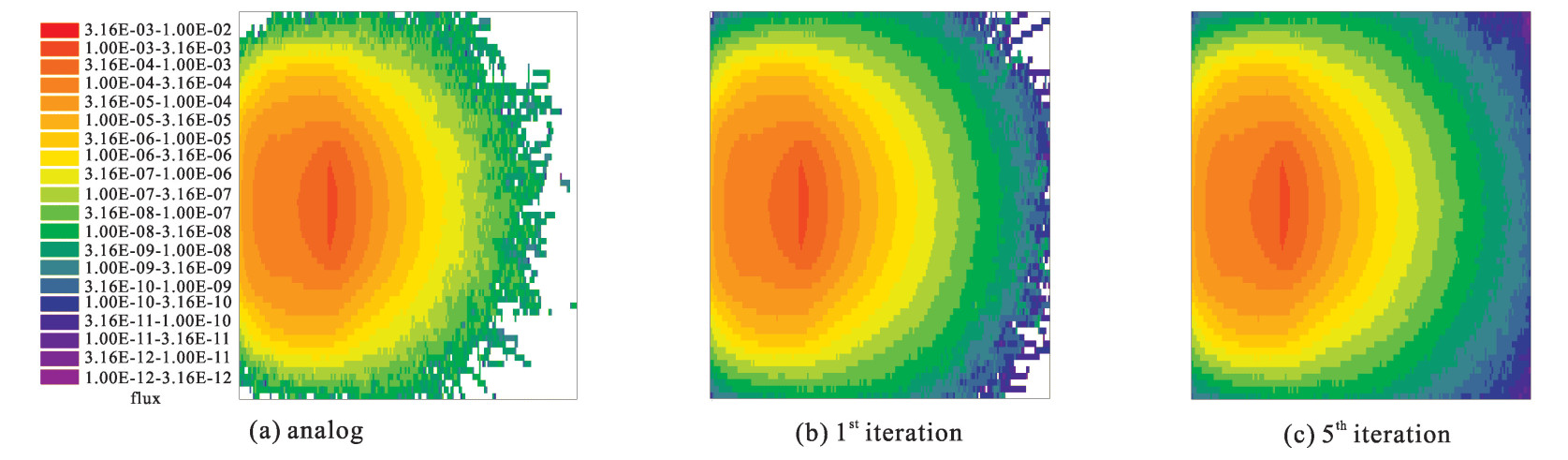
Global variance reduction based on forward Monte Carlo calculation
-
摘要: 蒙特卡罗方法是当前形势下辐射屏蔽计算的首选分析工具。小概率深穿透问题则是屏蔽计算的关键与亟待解决的核心问题，需要使用有效的减方差技巧。针对全局问题，利用蒙特卡罗正算输运得到的粒子通量或探测响应来构建权重窗参数，将现有的粒子位置偏移拓展到位置和能量偏倚。利用国际屏蔽基准题进行测试验证，通过使用该方法，粒子被引导到模型的所有位置。平均相对误差降低到10%以下，几乎所有网格区域都有粒子统计。结果表明，基于蒙特卡罗正算输运的输运偏倚参数构建方法能够实现全局减方差。Abstract: Monte Carlo method is extensively employed in radiation shielding calculation with the advantages of high fidelity geometry modeling, complex radiation source description and continuous-energy cross sections. However, the simulation is impractical for Monte Carlo particles that have little chance of being transported to the far-source area and the statistical error may be unacceptable. Accordingly, effective global variance reduction method (GVR) is significant for Monte Carlo deep-penetration radiation shielding calculation. This work constructs weight window parameters based on forward Monte Carlo calculation to bias the particles position and energy during transport. According to the validation of shielding benchmark, particles have been guided to far-source area by using the weight window. The relative error has been decreased to less than 10%, and almost all the mesh cells have been tallied. The results show that the transport parameters obtained from forward Monte Carlo calculation could realize global variance reduction.
-
Key words:
- Monte Carlo /
- forward transport /
- shielding calculation /
- global variance reduction
-
图 5 不同计算方案的相对误差分布
Figure 5. Relative error distribution of different calculation schemes
表 1 不同方案的计算结果
Table 1. Results of different calculation schemes
case time/min average relative error/% FOM empty mesh ratio/% sample rate/min-1 analog 30 57.76 0.066 32.96 1.521×105 1st iteration 30 32.34 0.145 9.906 0.827×105 2nd iteration 30 15.34 0.271 1.099 0.832×105 3rd iteration 30 10.37 0.527 0.055 0.845×105 4th iteration 30 9.100 0.540 0.001 25 0.836×105 5th iteration 30 8.130 0.545 0.000 42 0.848×105 
下载: 导出CSV
-
[1] Cooper M A, Larsen E W. Automated weight windows for global Monte Carlo particle transport calculations[J]. Nuclear Science and Engineering, 2001, 137: 1-13. doi: 10.13182/NSE00-34 [2] Becker T L, Larsen E W. The application of weight windows to global Monte Carlo problems[C]//Proc of International Conference on Mathematics, Computational Methods & Reactor Physics. 2009. [3] Becker T L. Hybrid Monte Carlo/deterministic methods for deep-penetration problems[D]. Michigan: University of Michigan, 2009. [4] Peplow D E, Blakeman E D, Wagner J C. Advanced variance reduction strategies for optimizing mesh tallies in MAVRIC[J]. Transactions of the ANS, 2007, 97: 595-597. [5] Wagner J C, Peplow D E, Mosher S W. FW-CADIS method for global and semi-global variance reduction of Monte Carlo radiation transport calculations[J]. Nuclear Science and Engineering, 2014, 177: 37-57. [6] Wijk Van A J, den Eynde Van G, Hoogenboom J E. An easy to implement global variance reduction procedure for MCNP[J]. Annals of Nuclear Energy, 2011, 38: 2496-2503. doi: 10.1016/j.anucene.2011.07.037 [7] Fan X, Zhang G, Wang K. Development of new variance reduction methods based on weight window technique in RMC code[J]. Progress in Nuclear Energy, 2016, 90: 197-203. doi: 10.1016/j.pnucene.2016.03.023 [8] 邱有恒, 邓力, 李百文, 等. 基于MESH技术的伴随权重窗自动生成方法及其应用[J]. 原子能科学技术, 2014, 48(11): 2148-2152. https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201411039.htmQiu Youheng, Deng Li, Li Baiwen, et al. Automatic generation method mesh-based adjoint weight window and its application. Atomic Energy Science and Technology, 2014, 48(11): 2148-2152 https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201411039.htm [9] 郑征, 吴宏春, 曹良志, 等. 蒙特卡罗与离散纵标耦合方法在压水堆堆腔漏束计算中的应用[J]. 强激光与粒子束, 2013, 24(12): 2946-2950. doi: 10.3788/HPLPB20122412.2946Zheng Zheng, Wu Hongchun, Cao Liangzhi, et al. Application of Monte Carlo and discrete ordinate coupling method to pressurized water reactor cavity radiation streaming calculation. High Power Laser and Particle Beams, 2013, 24(12): 2946-2950 doi: 10.3788/HPLPB20122412.2946 [10] 韩静茹, 陈义学, 袁龙军, 等. 基于蒙特卡罗-离散纵标双向耦合方法的堆坑粒子注量率计算[J]. 原子能科学技术, 2014, 48(9): 1621-1626. https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201409016.htmHan Jingru, Chen Yixue, Yuan Longjun, et al. Particle fluence rate calculation of reactor pit based on MC-SN bidirectional coupled method. Atomic Energy Science and Technology, 2014, 48(9): 1621-1626 https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201409016.htm [11] 肖锋, 应栋川, 章春伟, 等. 离散纵标与蒙特卡罗耦合方法在反应堆屏蔽计算中的应用[J]. 核动力工程, 2014, 35(5): 9-12. https://www.cnki.com.cn/Article/CJFDTOTAL-HDLG201405003.htmXiao Feng, Ying Dongchuan, Zhang Chunwei, et al. Application of discrete ordinate and Monte-Carlo coupling method for reactor shielding calculation. Nuclear Power Engineering, 2014, 35(5): 9-12 https://www.cnki.com.cn/Article/CJFDTOTAL-HDLG201405003.htm [12] X-5 Monte Carlo Team. MCNP—a general Monte Carlo N-particle transport code, version 5[R]. LA-UR-03-1987. [13] 邱有恒, 邓力, 上官丹骅, 等. JMCT软件的自动源偏倚抽样功能及其应用[J]. 计算物理, 2016, 33(5): 593-598. https://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201605012.htmQiu Youheng, Deng Li, Shangguan Danhua, et al. Auto source particle biasing sampling function of JMCT and its application. Chinese Jounal of Computational Physis, 2016, 33(5): 593-598 https://www.cnki.com.cn/Article/CJFDTOTAL-JSWL201605012.htm [14] Peplow D E. Comparison of hybrid methods for global variance reduction in shielding calculations[J]. Transactions of the American Nuclear Society, 2012, 107: 512-515. [15] OECD-NEA. Ispra iron benchmark experiment (EURACOS)[EB/OL]. https://www.oecdnea.org/science/wprs/shielding/sinbad/eurac_fe/eufe-abs.htm. -
点击查看大图
图(5) / 表(1)
计量
- 文章访问数: 1331
- HTML全文浏览量: 281
- PDF下载量: 211
- 被引次数: 0
