两种电磁场谱间断元方法的比较

章阳; 王向晖; 张杰; 王建国; 齐红新

doi:10.11884/HPLPB201830.170169

两种电磁场谱间断元方法的比较

doi: 10.11884/HPLPB201830.170169

章阳^1,,
王向晖¹,
张杰¹,
王建国²,
齐红新^1, ,

1.
华东师范大学物理系生物物理研究所, 上海 200241
2.
西北核技术研究所, 西安 710024

基金项目:

国家自然科学基金项目 31600675

国家自然科学基金项目 61231003

详细信息

作者简介:
章阳(1993—), 男，硕士研究生，主要从事生物电磁学研究; 2452025149@qq.com

通讯作者:
齐红新(1974—)，男，博士，主要从事计算电磁学研究; flyerqhx@126.com

中图分类号: O441.4
计量
- 文章访问数: 1021
- HTML全文浏览量: 224
- PDF下载量: 165
- 被引次数: 0
出版历程
- 收稿日期: 2017-09-26
- 修回日期: 2017-10-11
- 刊出日期: 2018-02-15

Comparison of two discontinuous spectral element methods

1.
Institute of Biophysics, Department of Physics, East China Normal University, Shanghai 200241, China
2.
Northwest Institute of Nuclear Technology, P. O. Box 69-1, Xi'an 710024, China

摘要

摘要: 时域间断元方法是近年来电磁场计算领域的重要进展之一。将基函数的插值点和数值积分点重合的质量集中技术是降低该间断元方法质量矩阵存储开销和提高计算效率的重要手段。通过谐振腔、带通滤波器以及光子晶体内的电磁场等数值算例，在四边形网格上比较了传统的质量集中算法和近来提出的Weight-Adjust算法之间的差异。计算结果表明，尽管两种方法的存储量一样，但Weight-Adjust算法具有更高的精度。
- 间断伽辽金算法 /
- Maxwell方程 /
- 质量集中 /
- 谱方法
Abstract: This paper is concerned with the comparison of two spectral Discontinuous Galerkin Time-Domain (DGTD) methods for the solution of Maxwell's equations in two-dimensional space. The first scheme is based on the conventional mass-lumping technique, where the same set of points are chosen for both the interpolation base functions and the numerical integration of coefficients. The second scheme is a newly proposed approach, called the Weight-Adjusted discontinuous Galerkin (WADG) method. Several numerical examples are presented to evaluate the performance of the two methods. It is shown that although the two methods need the same storage capacity, the WADG method has higher accuracy.
- discontinuous Galerkin method /
- Maxwell equations /
- mass-lumping /
- spectral method

HTML全文

图 1 测量点处得到的模拟结果与参考值的误差比较

Figure 1. Comparison of simulation results with reference values at measuring point

下载: 全尺寸图片幻灯片

图 2 带通滤波器截面的几何模型

Figure 2. Geometrical model of bandpass filter's cross-section

下载: 全尺寸图片幻灯片

图 3 带通滤波器的散射系数

Figure 3. Scattering parameters of bandpass filter

下载: 全尺寸图片幻灯片

图 4 光子晶体的截面网格

Figure 4. Meshes of photonic crystal's cross-section

下载: 全尺寸图片幻灯片

图 5 光子晶体功率分配器的截面模型以及电磁场分布

Figure 5. Cross-section geometry and electromagnetic field distribution of photonic crystol power divider

下载: 全尺寸图片幻灯片

图 6 通道内某测量点处两组数据的绝对误差

Figure 6. Absolute error of two sets of data at measuring point

下载: 全尺寸图片幻灯片

参考文献(12)

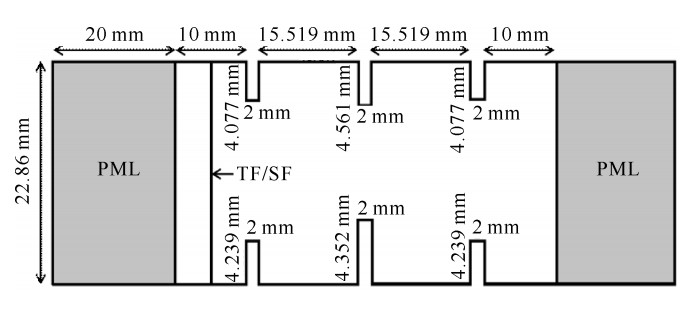
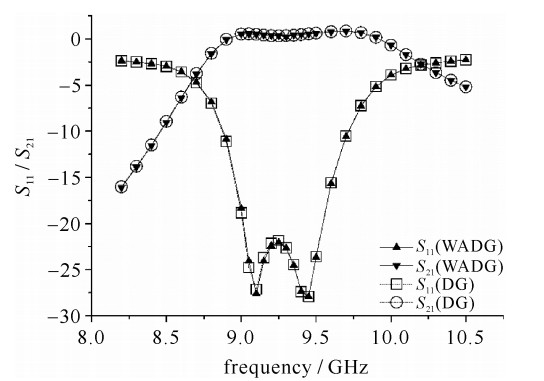
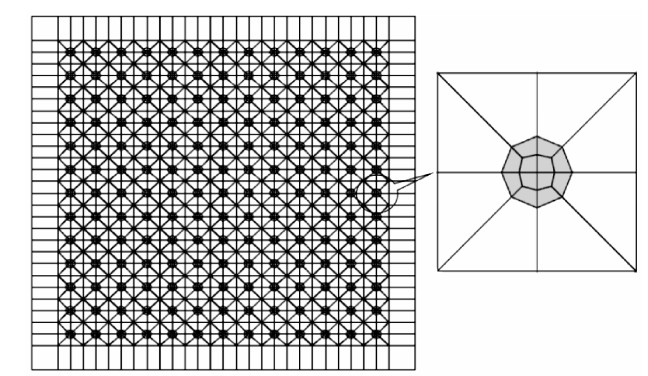
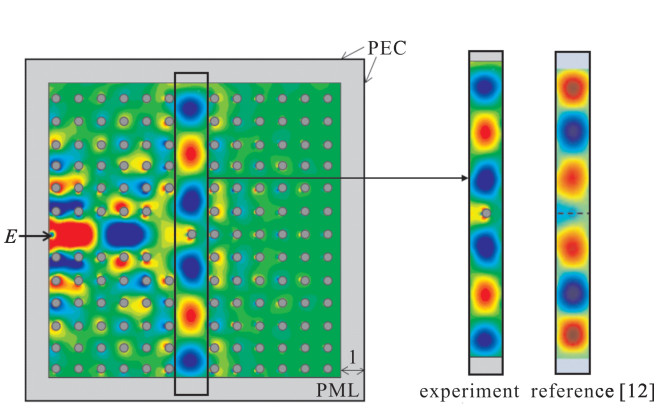
[1]	Stephane D, Clement D, Stephane L, et al. Recent advances on a DGTD method for time-domain electromagnetics[J]. Photonics and Nanostructures Fundamentals and Applications, 2013, 11(4): 291-302. doi: 10.1016/j.photonics.2013.06.005
[2]	Stephane D, Stephane L, Ludovic M. Temporal convergence analysis of a locally implicit discontinuous Galerkin time domain method for electromagnetic wave propagation in dispersive media[J]. Journal of Computational and Applied Mathematics, 2017, 316(15): 122-132.
[3]	Xiong Meng, Jennifer K R. Discontinuous Galerkin methods for nonlinear scalar hyperbolic conservation laws: divided difference estimates and accuracy enhancement[J]. Numerische Mathematik, 2017, 136(1): 27-73.
[4]	Zhu Jun, Zhong Xinghui, Shu Chiwang, et al. Runge-Kutta discontinuous Galerkin method with a simple and compact hermite WENO limiter on unstructured meshes[J]. Communications in Computational Physics, 2017, 21(3): 623-649.
[5]	Demirel A, Niegemann J, Busch K, et al. Efficient multiple time-stepping algorithms of higher order[J]. Journal of Computational Physics, 2015, 285(15): 133-148.
[6]	夏轶栋, 伍贻兆, 吕宏强. 高阶间断有限元法的并行计算研究[J]. 空气动力学报, 2011, 29(5): 537-541. https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201105000.htm Xia Yidong, Wu Yizhao, Lü Hongqiang. Parallel computation of a high-order discontinuous Galerkin method on unstructured grids. Acta Aerodynamica Sinica, 2011, 29(5): 537-541 https://www.cnki.com.cn/Article/CJFDTOTAL-KQDX201105000.htm
[7]	Liu Xiang, Kameni A, Serhir M, et al. 3D modeling with discontinuous Galerkin time domain method for ground penetration radar application[C]//GDR Ondes, Assemblee Generale Interferences d'Ondes, 2015.
[8]	Su Yan, Andrew D G, Jin Jianming. Modeling of plasma formation during high-power microwave breakdown in air using the discontinuous Galerkin time-domain method[J]. IEEE Journal on Multiscale and Multiphysics Computational Techniques, 2016, 27(1): 2-13.
[9]	Nikolai S, Claire S, Stephane L, et al. A DGTD method for the numerical modeling of the interaction of light with nanometer scale metallic structures taking into account non-local dispersion effects[J]. Journal of Computational Physics, 2016, 316(7): 396-415.
[10]	Chan J, Hewett R J, Warburton T. Weight-adjusted discontinuous Galerkin methods: wave propagation in heterogeneous media[OL]. arXiv, 2016.
[11]	Anderson W K, Wang Li, Kapadia S, et al. Petrov-Galerkin and discontinuous Galerkin methods for time-domain and frequency-domain electromagnetic simulations[J]. Journal of Computational Physics, 2011, 230(23): 8360-8385.
[12]	Liu Meilin, Sirenko K, Bagci H. An efficient discontinuous Galerkin finite element method for highly accurate solution of Maxwell equations[J]. IEEE Trans Antennas and Propagation, 2012, 60(8): 3992-3998.