Three-dimensional Monte Carlo transport code JMCT in shielding engineering application
-
摘要: 核设施辐射屏蔽计算，由于其大规模计算及深穿透等特性，一直是蒙特卡罗方法工程应用的难点之一。采用我国自主研发的三维中子-光子蒙特卡罗粒子输运模拟软件JMCT，结合可视化建模工具JLAMT，对OECD国际基准例题Winfrith Iron/Water Benchmark Experiment(ASPIS)两例实验装置进行建模与计算分析, 并将计算结果与实验值及MCNP计算值进行对比。结果表明，JMCT计算值与MCNP计算值符合较好，其中Winfrith Iron Benchmark Experiment(ASPIS)最大偏差不超过7%，平均偏差1.3%；Winfrith Water Benchmark Experiment(ASPIS)最大偏差小于20%，平均偏差小于10%，证明了JMCT在屏蔽计算以及深穿透问题的可靠性与工程应用性。Abstract: Radiation shielding calculation of nuclear facilities has always been one of the difficulties in engineering application of Monte Carlo method for its large scale calculation and deep penetration characteristics. Two international benchmarks, published by OECD, Winfrith Iron/Water Benchmark Experiment(ASPIS), were simulated based on the three-dimensional Monte Carlo transport code JMCT, accompanied by a visual modeling tool JLAMT. The simulation includes detailed modeling and shielding calculation. Calculated results were compared with experimental data, also with almost same results achieved by MCNP. The comparisons show that the calculated results agree well with the experimental data. The maximum deviation of JMCT and MCNP is below 20% and the average deviation is less than 10%. It is proved that JMCT code suits well for shielding simulation and deep penetration problems.
-
Key words:
- Monte Carlo /
- deep penetration /
- JMCT /
- JLAMT /
- shielding transportation
-
在反应堆领域，屏蔽问题无论是对于反应堆设计、安全分析还是辐射防护都至关重要，因此在核电站设计中，对核设施进行屏蔽计算分析是一项非常重要的工作。由于受物理条件的限制，为了得到所需的结果，必须借助理论计算[1]。通常，在反应堆数值模拟中，经常使用的求解中子-光子输运问题的求解方法包括确定论方法和蒙特卡罗方法[2-3]。相比于确定论方法，蒙特卡罗方法具有几何描述精确、物理过程描述保真等优点。但是另一方面，作为一种概率统计方法，蒙特卡罗方法对于求解具有较大计算规模和深穿透特性的屏蔽问题，要获得值得信任的计算结果往往需要极大的计算成本，因此，以往受限于计算机软硬件条件，蒙特卡罗方法一直没有得到广泛的工程应用。进入21世纪以来，随着计算机技术的飞速发展以及反应堆物理分析的不断深入，对数值模拟的计算精度要求越来越高，蒙特卡罗方法因其突出的优点而在反应堆设计、安全分析等领域受到了越来越多的关注。
自20世纪以来，国内外多家研究机构都相继开展了以蒙特卡罗方法为理论基础的蒙卡软件的研发工作。国际上有美国Los Alamos国家实验室研发的MCNP[4]程序，美国Oak Ridge国家实验室开发的MORSE和KENO[5]程序，美国麻省理工学院开发的OpenMC[5]程序，日本BNFL同AEA Technology合作开发的MCBEND[6]程序等。国内主要有由中国科学院核能安全技术研究所FDS团队开发的SuperMC[7]，由清华大学工程物理系核能科学与工程管理研究所反应堆工程计算研究所(REAL团队)开发的RMC[8]，由国家核电技术有限公司北京软件技术中心与清华REAL团队联合开发的CosRMC[9]，以及由北京应用物理与计算数学研究所开发的JMCT[10]。
本文选取两例OECD国际基准例题Winfrith Iron/Water Benchmark Experiment(ASPIS)，使用JMCT与其配套前处理可视化建模工具JLAMT进行精细建模计算，将计算结果与MCNP计算结果及实验测量值进行对比分析，以验证JMCT对于深穿透屏蔽工程问题的计算能力。
1. JMCT软件介绍
JMCT是中物院高性能数值模拟软件中心——粒子输运团队自主研发的蒙特卡罗粒子输运模拟软件。该软件目前可模拟中子、光子输运及其耦合输运模式，适用于对固定源、系统临界本征值以及输运-燃耗耦合计算问题的模拟。与MCNP等蒙特卡罗粒子输运程序类似，JMCT软件具有物理计算精细、几何描述精确等优点。JMCT计算模型的建立依赖于其配备的前处理可视化建模软件JLAMT。JLAMT采用引导式可视化CAD建模方式，避免了像MCNP程序中复杂的面方程定义，便于掌握，建模出错率低，且建模完成后可将CAD建模过程中的实体与操作转化为GDML语言，极大地方便了用户的使用，具有很强的通用型与可扩展性。
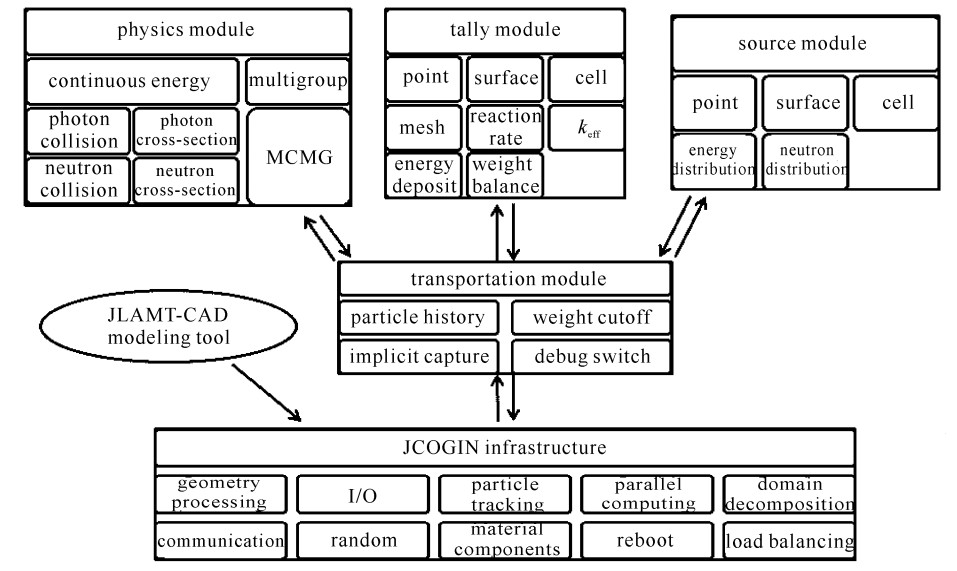
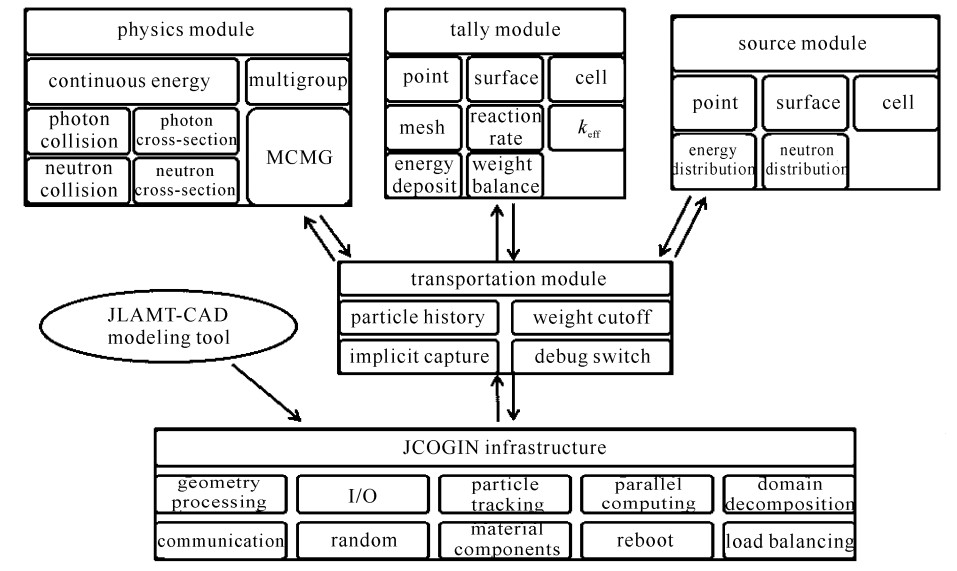
JMCT采用框架开发模式[11]，如图 1所示，支持多平台的进程与线程两级并行运行机制，结合逻辑上的粒子并行与区域分解两种并行方式，能够有效解决大量运算对于计算速度与内存量的需求。此外，JMCT的输入文件以“字段=值”的书写方式为用户提供多种使用功能选项，如模拟问题类别、输运能量模式、源与记数设置等，便于书写与阅读，且程序内部自带很多初始默认设置，简化了用户的输入。
JMCT软件整合了先进算法、大规模并行、可视化精细建模等实用技术，可以实现对各种复杂粒子输运系统的快速精确模拟，这对于解决蒙特卡罗方法工程应用中的难点问题——屏蔽计算问题显示出很大的优势。这类问题普遍具有大规模计算及深穿透的特性，模拟计算过程的理想状态是在实现高置信度模拟的同时有尽可能快的计算速度，JMCT在屏蔽分析计算中可以使用一定的降低方差的技巧或者采用高效的并行处理器。
2. 基准题模型与JMCT建模
为了验证JMCT在屏蔽工程问题中的应用性与可靠性，本文选取Winfrith Iron Benchmark(ASPIS) [12]与Winfrith Water Benchmark Experiment (ASPIS)[13]两例屏蔽实验装置进行建模计算，上述模型均为典型深穿透问题，粒子从源位置穿透至探测器位置需要经历数十个自由程，中子通量密度梯度非常大，探测器计数十分困难，对蒙卡程序计算非常具有挑战性。
2.1 Winfrith Iron Benchmark(ASPIS)
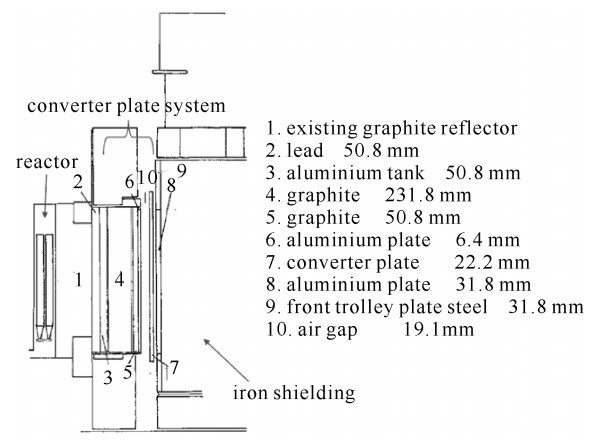
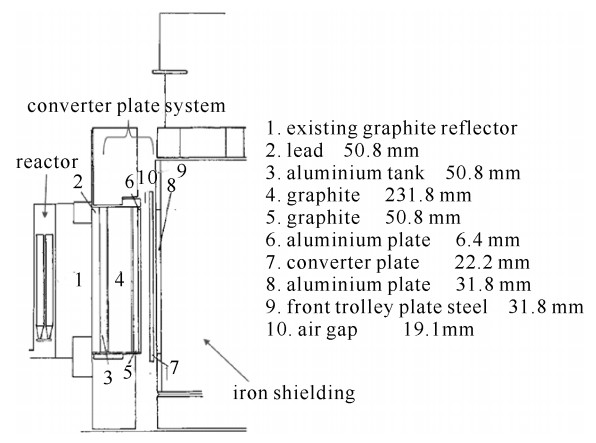
该基准实验在Winfrith英国原子能研究机构的ASPIS通用屏蔽装置上进行。实验需要测量1 m厚大块铁屏蔽体不同深度情况下的中子能谱和反应率。实验装置安装在一个反应堆功率为30 kW的轻水冷却、石墨和轻水慢化的NESTOR反应堆上，实验装置的整体布局如图 2所示，图中所标注尺寸均以mm为单位。通过NESTOR中子源驱动天然铀转换靶提供一个截面近似圆盘的裂变中子源，转换靶靠近堆芯一侧裂变率的空间分布由经过校准的0.05 mm厚的天然铀箔测量，测量结果沿着方位角环向进行平均。该实验需要测量1 m厚大块铁屏蔽体不同深度情况下的中子能谱和反应率，由于在该基准题模型中屏蔽层非常厚，粒子的穿透距离比较长，因而，随着穿透距离的增加计数粒子与通量密度数呈指数衰减。关于实验装置的详细几何及材料参数见参考文献[12]。
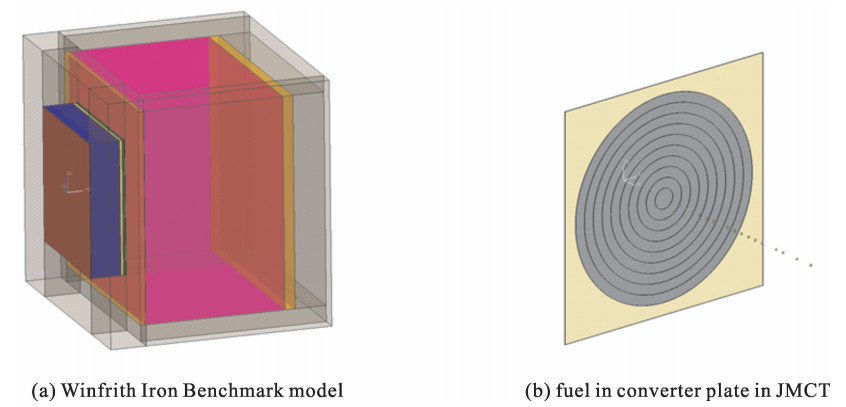
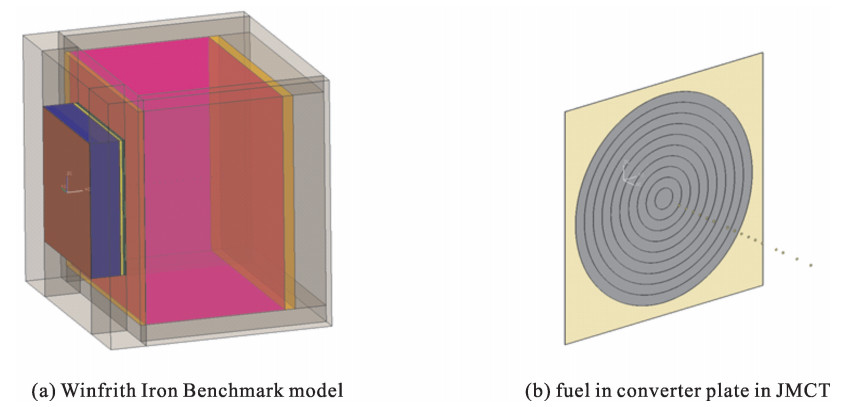
图 2 Winfrith Iron Benchmark(ASPIS)实验装置整体布置Figure 2. Layout of Winfrith Iron Benchmark(ASPIS)在使用JMCT建模的过程中，按照基准报告建议，包括裂变板在内的实验装置为了更适用于计算都做了一定程度的近似，再辅以一些修正因子加以修正。整体模型如图 3(a)所示。
图 3 Winfrith Iron Benchmark模型JMCT建模图Figure 3. Sectional view of Winfrith Iron Benchmark model转换靶源项为截面近似圆盘的圆柱源，功率在轴向和周向上为均匀分布，径向近似为一个宽度为142.9 cm的余弦分布，如公式(1)所示，f(r)即为表示径向功率分布的余弦函数，能量分布采用Watt谱近似
$$ f(r)=A \nu_{235} \cos \frac{\pi r}{142.9} $$ (1) 式中：r代表圆盘半径，0 < r < 59.3 cm；ν235=2.437，为235U裂变中子份额；A=3346 s-1·cm-2·W-1。
由于JMCT暂不支持余弦分布描述，因此，我们采用概率分布的方式来近似描述这种余弦分布，将圆柱源沿径向按等距离间隔分为10层圆环，如图 3(b)所示，每层圆环对应的概率
$$ p_n=\int_{R_1}^{R_n} A \nu_{235} \cos \left(\frac{\pi r}{142.9}\right) r \mathrm{~d} r=\left.A \nu_{235}\left[\frac{142.9^2}{\pi^2} \cos \left(\frac{\pi r}{142.9}\right)+\frac{142.9 r}{\pi} \sin \left(\frac{\pi r}{142.9}\right)\right]\right|_{R_{n-1}} ^{R_n} $$ (2) 式中：R1为第一个圆环的半径; Rn为第n个圆环的半径; pn为对应于第n个圆环的抽样概率。
转换靶内总的源强
$$ P_{\mathrm{tot}}=\int_0^R 2 \pi r f(r) \mathrm{d} r=5.527 \times 10^7\left(\mathrm{n} \cdot \mathrm{s}^{-1}\right) $$ (3) 式中：R为圆环半径。
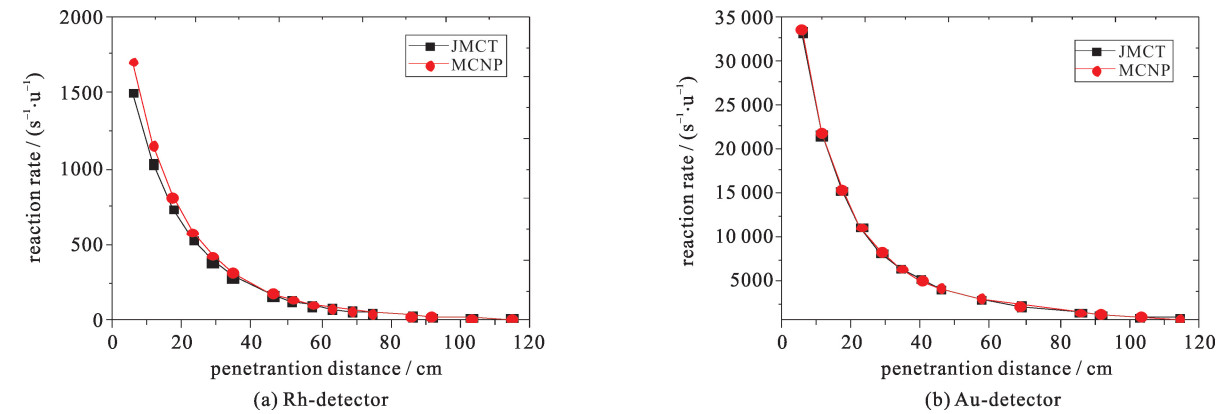
实验测量了103Rh(n, n′)，197Au(n, γ)两种探测器的反应率，采用NE213闪烁体探测器测量能谱。由于粒子穿透距离过长，抽样粒子模拟效率低，为了克服深穿透效应，减少计算时间来使计算结果收敛到可接受的范围，采用了设置柵元重要性的降方差方法和并行计算的方式来提升计算效率，增大统计量，减小统计误差。总模拟粒子数规模为1×108。
2.2 Winfrith Water Benchmark(ASPIS)
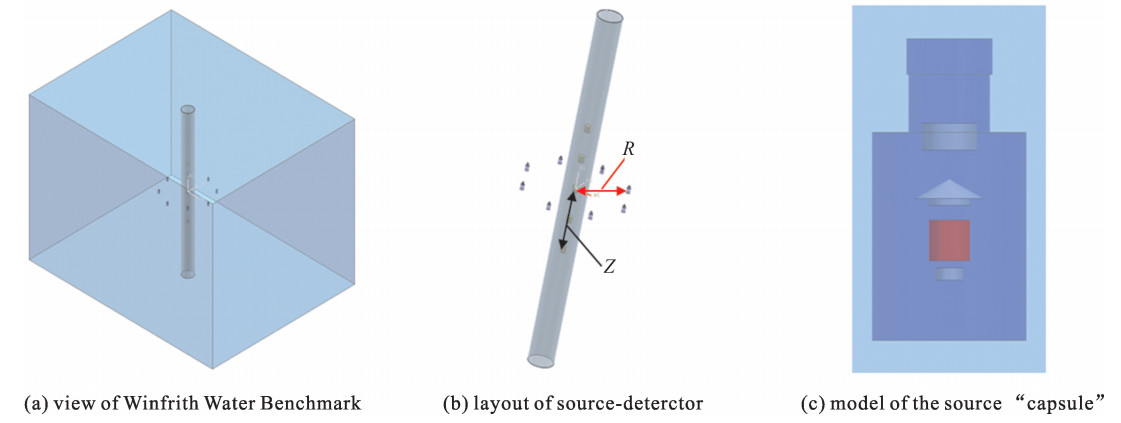
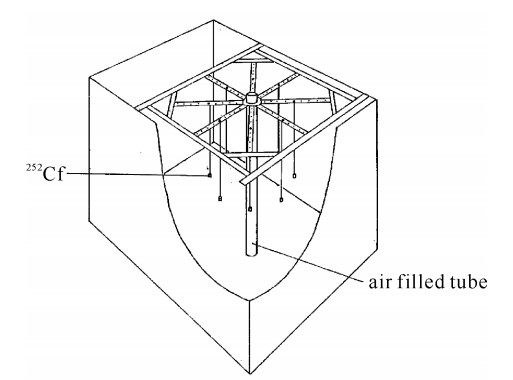
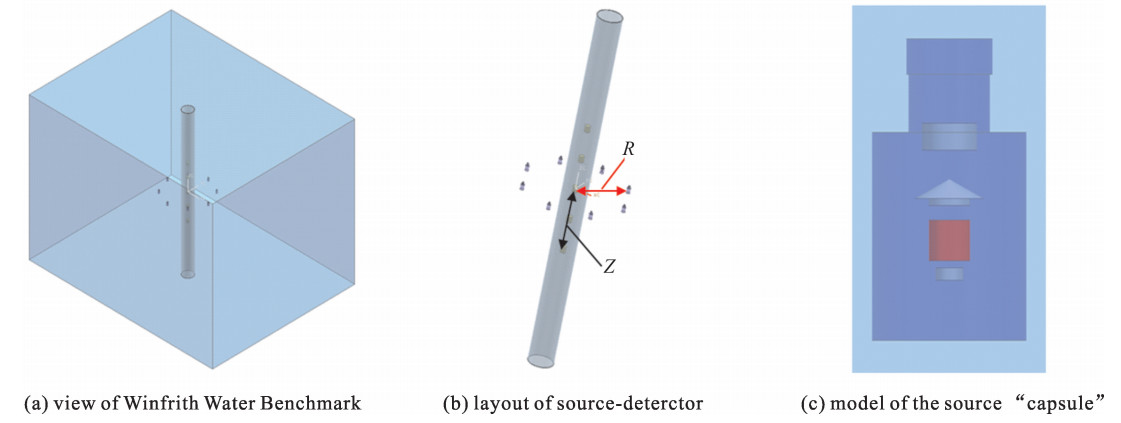
该基准实验的实验中子源由252Cf瞬发裂变源提供，实验需要测量1 MeV以上的快中子能谱和穿透50 cm厚度水的反应率，完整的实验布置包括一个大的水箱以及一个放置在水箱中央的由空气填充的测量铝管，铝管内安置着进行测量的探测器，8个独立的、已被标定的252Cf中子源均匀对称的分布在测量铝管的周围，如图 4所示。实验过程中8个中子源可以以50.8 mm的步长在径向平面内移动来改变源-探测器所在测量管之间的距离(即源与测量管轴心的距离，图 5中用R表示出)，从而达到不同的源项配置的实验方案，如表 1所示，表格中还包含了源强(即每秒产生的粒子数)信息以及模拟计算中的粒子数规模。中子源与水箱外壁的最近距离约为38 cm，约为5 MeV中子在水中的迁徙长度的4倍，所以源-探测器布置可视作浸入无限大水中。实验装置详细的几何及材料参数见参考文献[13]。
图 4 Winfrith Water Benchmark(ASPIS)实验装置整体布置Figure 4. Layout of Winfrith Water Benchmark(ASPIS)
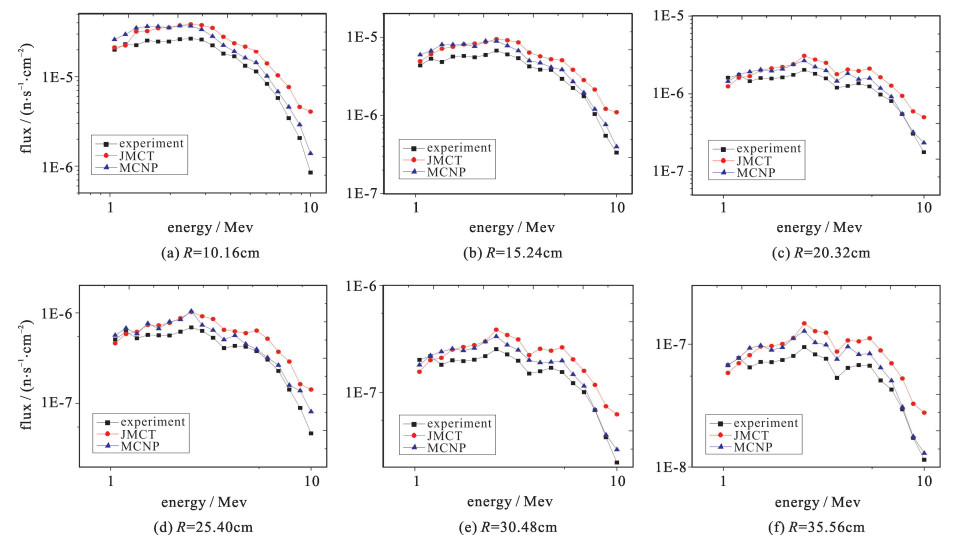
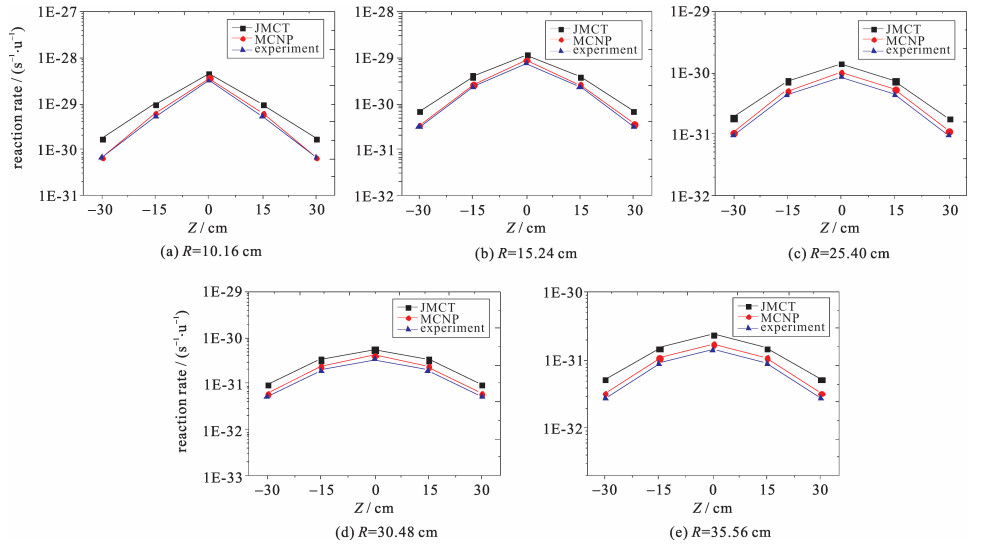
图 5 Winfrith Water Benchmark模型JMCT建模图Figure 5. Sectional view of Winfrith Water Benchmark model表 1 Winfrith Water Benchmark实验不同源项配置方案及相应模拟粒子数规模Table 1. Experimental source arrangements and scale of simulated particles in different cases for Winfrith Water Benchmarkcase source-detector spacing/cm number of sources total source strength/(n·s-1) particles 1 10.16 1 1.256 0×107 4×107 2 15.24 2 2.540 0×107 2×108 3 20.32 4 5.260 0×107 2×108 4 25.40 8 1.048 0×108 2×108 5 30.48 8 1.046 0×108 1×109 6 35.56 8 1.048 0×107 1×109 7 50.80 8 1.044 5×108 1×109 本基准实验测量了S32(n, p)P32探测器的反应率，探测器在测量管内沿轴向布置，与源所在水平面距离(即探测器位置，图 5中用Z表示)分别为0，±15，±30 cm，对应于源-探测器距离分别为10.16，15.24，25.40，30.48，35.56 cm时进行测量。使用NE213液体闪烁体探测器测量能量大于1 MeV的中子能谱，仅在水平0 cm处进行测量。JMCT模型如图 5所示，为了不同源项配置方案下的计算结果都达到收敛，模拟粒子数的规模视不同的源项配置方案而定，如表 1所示。
3. 计算结果与分析
3.1 Winfrith Iron Benchmark结果分析
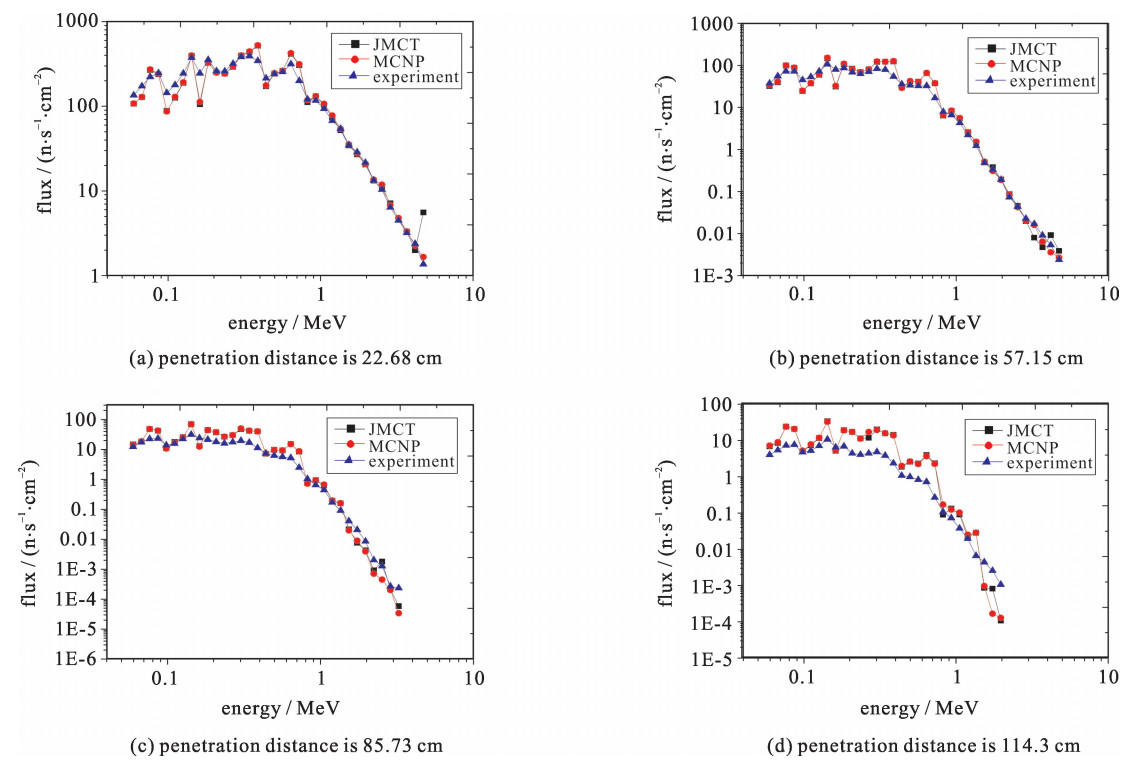
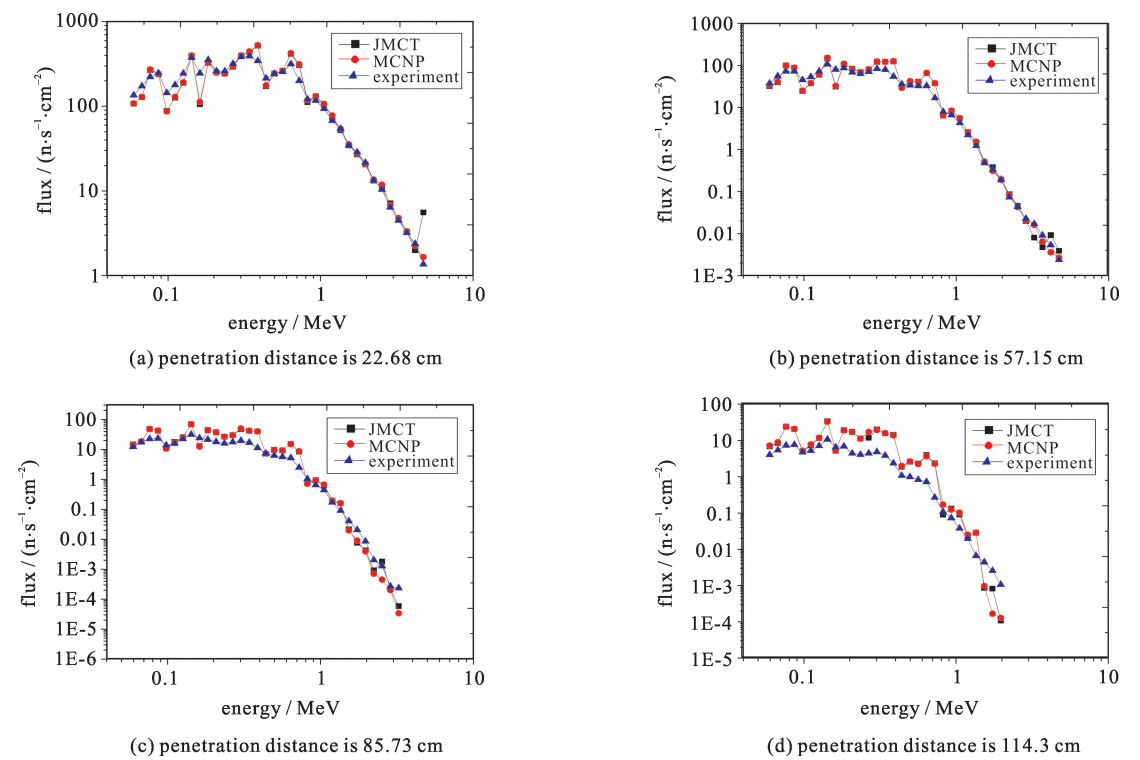
本文根据文献[12]中给出的探测器测量点的位置，在相应位置上进行通量计数，并采用文献[12]中的能群结构进行能谱计数。中子能谱的测量位置分别在铁屏蔽体中的穿透距离为22.68，57.15，85.73，114.3 cm处。为了克服深穿透效应，获得更好的计算结果，采用F5点探测器计数进行中子能谱测量。结果表明，不论是中子能谱还是反应率，JMCT的计算结果与实验测量值基本符合良好，将其计算结果与相同模型和设置下的MCNP计算结果进行比较，JMCT和MCNP中子通量计数最大偏差为18%。
图 6为不同穿透距离时, JMCT，MCNP计算值及基准报告中实验值的对比，可以看出：穿透距离为22.68，57.15，85.73 cm时JMCT计算结果与实验测量值及MCNP计算值均吻合良好，但当穿透距离增加到114.3 cm时，JMCT计算结果与实验测量值相比偏高，但与MCNP计算值吻合良好，考虑因为粒子穿透距离太长，实际测量中受各种环境条件因素的影响更难统计到粒子数，因此JMCT与MCNP的计算值均比实验值偏高。
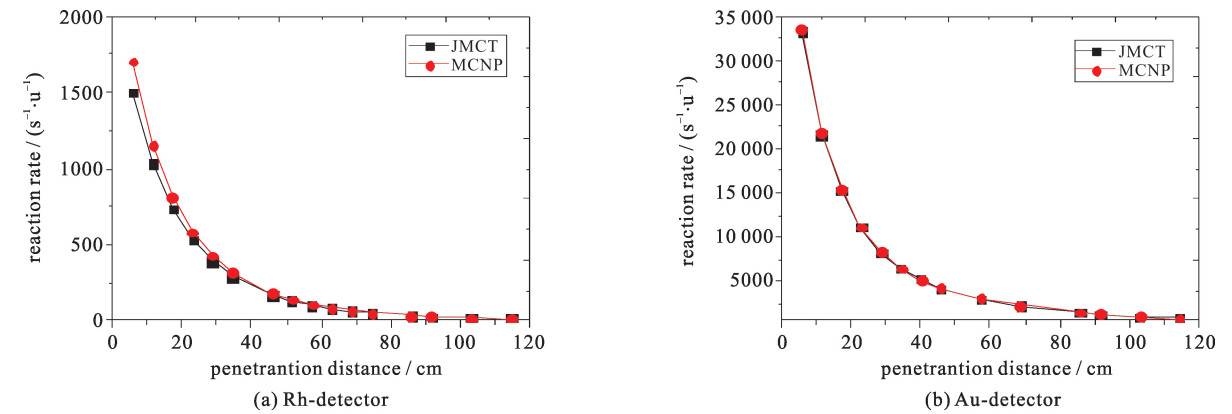
图 6 Winfrith Iron Benchmark不同穿透距离下的中子通量能谱Figure 6. Neutron flux energy spectra for Winfrith Iron Benchmark图 7为JMCT计算的Rh探测器和Au探测器的反应率与MCNP计算结果的比较，其中反应率的单位为每个原子每秒的衰变次数, 可以看出，屏蔽体内不同深度下JMCT计算结果与MCNP结果符合较好，Rh探测器最大偏差不超过3%，平均偏差0.5%，Au探测器最大偏差不超过7%，平均偏差1.3%。偏差存在的原因可能是由于JMCT计算所采用的核数据库是ENDF/B-VII.0，而MCNP采用的是ENDF/B-VI库所致。
图 7 JMCT和MCNP计算的Rh和Au探测器在屏蔽体内不同深度下的反应率Figure 7. Reaction rate of Rh and Au detector in different depth calculated by JMCT and MCNP3.2 Winfrith Water Benchmark结果分析
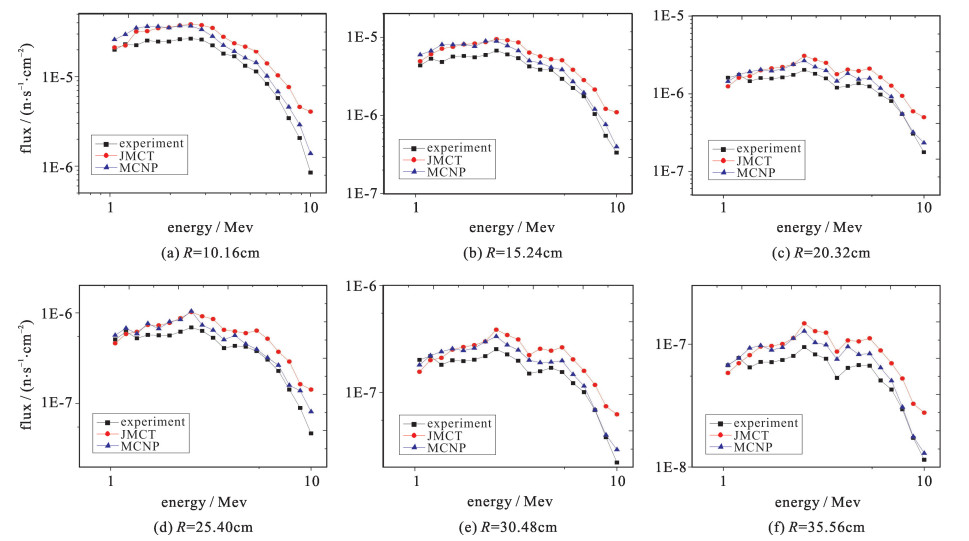
根据文献[13]中所给出的不同的源项配置方案，在其给出的相应探测器测量点位置进行通量计数，并采用其中的能群结构进行能谱计数, 计算结果如图 8所示。可以看出，JMCT计算结果与实验测量值相比整体趋势一致，基本吻合。但在高能区相对误差偏大，部分能量点出现突跳现象。将其与MCNP计算结果进行对比，平均偏差10%, 最大偏差接近20%，可以看出，JMCT计算结果与MCNP在低能区吻合良好，高能区偏高。
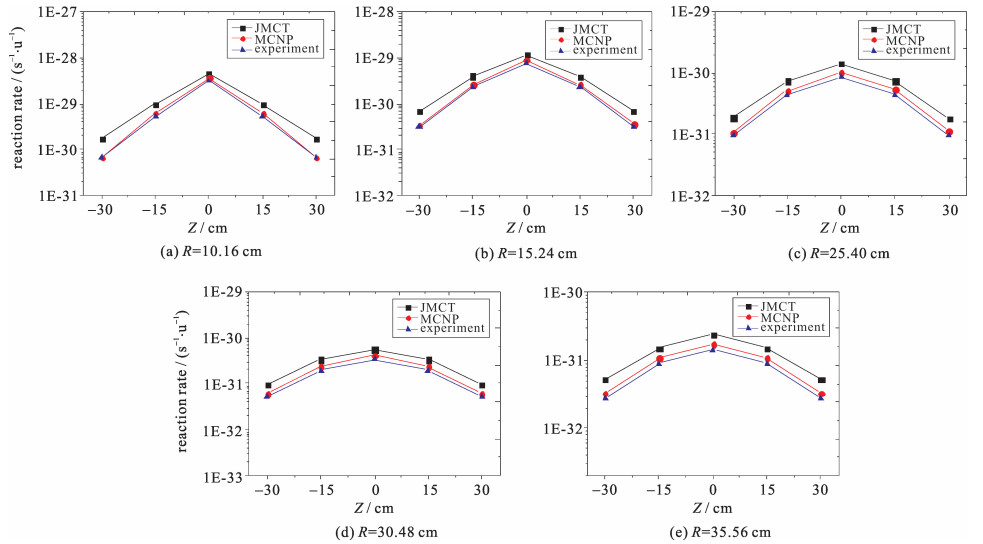
图 8 Winfrith Water Benchmark不同源项配置方案下的中子通量能谱Figure 8. Neutron flux energy spectra of different source-detector spacing for Winfrith Water Benchmark图 9是不同源项配置方案下S探测器的反应率测量结果，横坐标为中央测量管内探测器与源所在水平面的距离。JMCT计算结果与实验测量值比MCNP计算值略高，这种现象对于距离源所在水平面较远的探测器表现更为明显，尤其在只有一个源的实验方案时，当源数目增加后，偏差呈现明显减小的趋势。
图 9 Winfrith Water Benchmark不同源项配置方案下S探测器的反应率Figure 9. S detectors' reaction rate of different source-detector spacing R for Winfrith Water Benchmark4. 结论
本文使用JMCT程序对Winfrith Iron/Water Benchmark Experiment(ASPIS)两例基准题的精细建模，并计算相应位置的中子能谱以及指定探测器的反应率，计算结果与实验测量值比较符合良好。对于偏差较大的计算结果，进一步采用与相同模型和设置下的MCNP计算结果进行比对，结果最大偏差小于20%，平均偏差小于10%，表明了JMCT程序物理模型正确，计算结果与精度可靠。此外，使用JMCT计算过程中使用的降方差技巧以及并行计算的方式，对于提高计算效率、增大统计量、减少统计误差效果显著。综上所述，JMCT在解决屏蔽计算以及深穿透问题的能力与MCNP相当，显示了它在核设施屏蔽计算类问题中的可靠性与工程应用性。
致谢: 感谢北京应用物理与计算数学研究所、中物院高性能数值模拟软件中心提供JMCT软件并给予指导帮助。 -
图 2 Winfrith Iron Benchmark(ASPIS)实验装置整体布置
Figure 2. Layout of Winfrith Iron Benchmark(ASPIS)
图 3 Winfrith Iron Benchmark模型JMCT建模图
Figure 3. Sectional view of Winfrith Iron Benchmark model
图 4 Winfrith Water Benchmark(ASPIS)实验装置整体布置
Figure 4. Layout of Winfrith Water Benchmark(ASPIS)
图 5 Winfrith Water Benchmark模型JMCT建模图
Figure 5. Sectional view of Winfrith Water Benchmark model
图 6 Winfrith Iron Benchmark不同穿透距离下的中子通量能谱
Figure 6. Neutron flux energy spectra for Winfrith Iron Benchmark
图 7 JMCT和MCNP计算的Rh和Au探测器在屏蔽体内不同深度下的反应率
Figure 7. Reaction rate of Rh and Au detector in different depth calculated by JMCT and MCNP
图 8 Winfrith Water Benchmark不同源项配置方案下的中子通量能谱
Figure 8. Neutron flux energy spectra of different source-detector spacing for Winfrith Water Benchmark
图 9 Winfrith Water Benchmark不同源项配置方案下S探测器的反应率
Figure 9. S detectors' reaction rate of different source-detector spacing R for Winfrith Water Benchmark
表 1 Winfrith Water Benchmark实验不同源项配置方案及相应模拟粒子数规模
Table 1. Experimental source arrangements and scale of simulated particles in different cases for Winfrith Water Benchmark
case source-detector spacing/cm number of sources total source strength/(n·s-1) particles 1 10.16 1 1.256 0×107 4×107 2 15.24 2 2.540 0×107 2×108 3 20.32 4 5.260 0×107 2×108 4 25.40 8 1.048 0×108 2×108 5 30.48 8 1.046 0×108 1×109 6 35.56 8 1.048 0×107 1×109 7 50.80 8 1.044 5×108 1×109 
下载: 导出CSV
-
[1] 许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京: 原子能出版社, 2006.Xu Shuyan. Application of Monte Carlo method in experimental nuclear physics. Beijing: Atomic Energy Press, 1980 [2] 谢仲生, 张育曼, 张建民, 等. 核反应堆物理数值计算[M]. 北京: 原子能出版社, 1997.Xie Zhongsheng, Zhang Yuman, Zhang Jianmin, et al. Nuclear reactor physics numerical calculation. Beijing: Atomic Energy Press, 1997 [3] 裴鹿成, 张孝泽. 蒙特卡罗方法及其在粒子输运问题中的应用[M]. 北京: 科学出版社, 1980.Pei Lucheng, Zhang Xiaoze. Monte Carlo method and its application in particle transport problem. Beijing: Science Press, 1980 [4] X-5 Monte Carlo Team. MCNP: A general Monte Carlo N-particle transport code[R]. LA-CP-03-0248, 2003. [5] Emmett M B, Hollenbach D F. Current status of the Oak ridge Monte Carlo Codes: MORSE/SAS4 and KENO[R]. Computational Physics and Engineering Division, 2000. [6] Cowan P, Dobson G, Wright G A, et al. Recent developments to the Monte Carlo code MCBEND[J]. Nuclear Technology, 2009, 168(3): 780-784. doi: 10.13182/NT09-A9306 [7] 吴宜灿, 宋婧, 胡丽琴, 等. 超级蒙特卡罗核计算仿真软件系统SuperMC[J]. 核科学与工程, 2016, 36(1): 62-71. https://www.cnki.com.cn/Article/CJFDTOTAL-HKXY201601009.htmWu Yican, Song Jing, Hu Liqin, et al. Super Monte Carlo calculation program SuperMC. Chinese Journal of Nuclear Science and Engineering, 2016, 36(1): 62-71 https://www.cnki.com.cn/Article/CJFDTOTAL-HKXY201601009.htm [8] 佘顶, 梁金刚, 李泽光, 等. 堆用蒙卡程序RMC-Beta2.0用户使用手册[M]. 北京: 清华大学, 2013.She Ding, Liang Jingang, Li Zeguang, et al. Users' manual for Reactor Monte Carlo code RMC-Beta2.0. Bejing: Peking University, 2013 [9] 佘顶, 丘意书, 王侃. 反应堆蒙特卡罗分析软件CosRMC内部测试版用户手册[M]. 北京: 清华大学, 2015.She Ding, Qiu Yishu, Wang Kan. Users' manual for Reactor Monte Carlo code CosRMC internal testing. Bejing: Peking University, 2015 [10] 邓力, 李刚, 李瑞, 等. 三维蒙特卡罗粒子输运软件JMCT用户使用手册(V2.0版)[M]. 北京: 北京应用物理与计算数学研究所, 2015.Deng Li, Li Gang, Li Rui, et al. Users' manual for three dimensional Monte Carlo particle transport code JMCT version2.0. Beijing: Insitute of Applied Physics and Computational Mathematics, 2015 [11] 张宝印, 李刚, 邓力. 组合几何蒙特卡罗粒子输运支撑软件框架JCOGIN介绍[J]. 强激光与粒子束, 2013, 25(1): 173-176. doi: 10.3788/HPLPB20132501.0173Zhang Baoyin, Li Gang, Deng Li. JCOGIN: a combinatorial geometry Monte Carlo particle transport infrastructure. High Power Laser and Particle Beams, 2013, 25(1): 173-176 doi: 10.3788/HPLPB20132501.0173 [12] Butler J, Carter M D, McCracken A K, et al. Packwood: Results and calculational model of the Winfrith Iron Benchmark Experiment[R]. NEACRP-A-629, 1984. [13] Carter M D, Packwood A. The Winfrith Water Benchmark Experiment[R]. NEACRP-A-628, 1984. 期刊类型引用(6)
1. 车锐，刘仕倡，田卓，陈义学. 基于SINBAD聚变基准题的cosRMC程序屏蔽计算研究. 核技术. 2024(05): 75-85 . 
百度学术2. 张芳，董志伟，柴辰睿，周海京，安建祝，赵强，薛碧曦. 基本舰船结构的辐射屏蔽因子研究. 强激光与粒子束. 2024(12): 125-132 . 本站查看3. 刘鹏，史敦福，李瑞，付元光，邓力. 基于蒙特卡罗程序JMCT模拟计算堆芯物理基准题VERA. 原子能科学技术. 2023(06): 1131-1139 . 百度学术4. 刘利，左应红，牛胜利，朱金辉，李夏至. 中子在大气中产生氮俘获γ的蒙特卡罗模拟研究. 强激光与粒子束. 2022(08): 162-168 . 本站查看5. 黎辉，王梦琪，郑征. CAP1400核电厂堆腔辐射漏束屏蔽设计研究. 核科学与工程. 2021(02): 230-235 . 百度学术6. 李锐，张显，刘仕倡，全国萍，秦瑶，严伊蔓，陈义学. 蒙特卡罗粒子输运程序cosRMC的深穿透屏蔽计算研究. 原子能科学技术. 2021(S1): 82-87 . 百度学术其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 1545
- HTML全文浏览量: 286
- PDF下载量: 382
- 被引次数: 7
