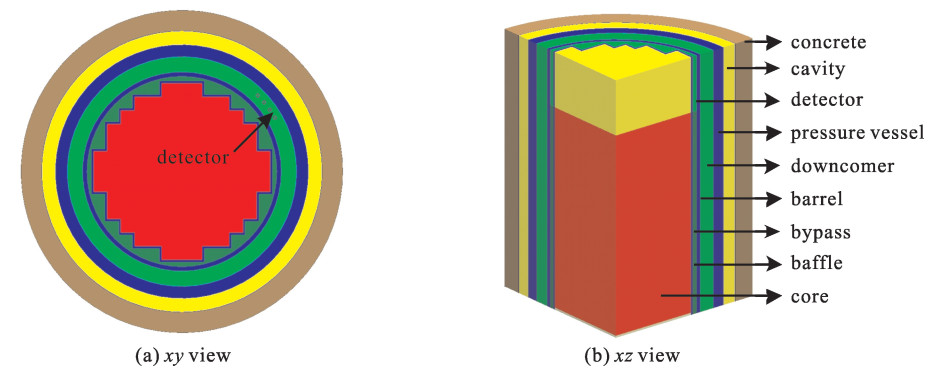
Variance reduction method based on adjoint discrete ordinate
-
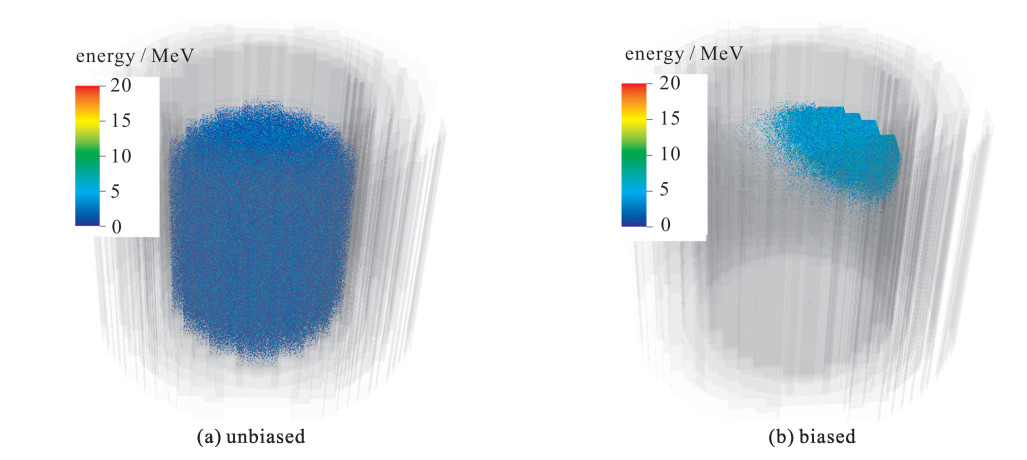
摘要: 对于深穿透类型的屏蔽计算，为了得到较为可信的统计结果，蒙特卡罗方法(MC方法)需要模拟大量的粒子，巨大的计算时间是其存在的主要问题。源偏倚和权窗技巧能够有效降低深穿透问题的计数误差。开展了基于共轭离散纵标(SN)的MC减方差方法研究，根据SN方法的共轭注量率计算并生成了源偏倚和权窗参数，编写了JMCT程序的源抽样子程序，并且在秦山一期测量值基础上进行了验证，成功应用到CAP1400压力容器快中子注量率和堆腔中子和光子剂量率计算中。数值结果表明，对于深穿透屏蔽计算问题，和无偏的MC方法相比，基于共轭SN的MC减方差方法能够在保证结果精度的前提下，提高计算效率1~2个量级。Abstract: For deep-penetration shielding calculation, Monte Carlo method (MC method) requires modeling a great number of particles to obtain reliable results, thus huge computation time is the main problem of the MC method. Source biasing and weight window technique effectively decrease the tally error of deep penetration problem. This paper studies the variance reduction (VR) method based on adjoint Discrete Ordinate (SN), generates source biasing factors and weight window parameters for the MC method by using the adjoint fluence rates of the SN method, and develops source sampling subroutine for JMCT. The VR method was verified at phaseⅠ of Qinshan Nuclear Power Plant measurements. It was applied to CAP1400 pressure vessel fast neutron fluence rate and cavity neutron and photon dose rate calculations. Numerical results show that the VR method based on SN increases calculation efficiency by 1~2 orders for deep-penetration shielding calculation with high precision compared with unbiased MC method.
-
Key words:
- deep-penetration /
- discrete ordinate method /
- Monte Carlo method /
- source biasing /
- weight window
-
剥离注入是强流质子同步加速器中最常用的注入方法，剥离膜系统是其关键设备。中国散裂中子源的剥离膜系统主要包括RCS注入区的主剥离膜和次剥离膜。在散裂中子源工作过程中，注入区剥离膜的作用是极其关键的，是实现负氢离子转换为质子注入加速的关键设备。散裂中子源主剥离膜采用面密度100 μg/cm2、厚度为500 nm的类金刚石膜片。碳膜具有比热容高、导热性好、密度小、热膨胀系数低及高熔点等优点，其熔点高达3800 K，但是类金刚石剥离膜同时又具有超薄、易碎等物理特性，500 nm薄膜的安装及固定难度高，同时在真空获得过程中，过大的压差导致空气扰动极有可能造成膜片的损坏。本文主要研究剥离膜辅助安装装置，实现剥离膜样品批量安装，通过对剥离膜的空气动力学进行分析，研究剥离膜片在真空获得过程中可能出现的膜片破坏情况，制定可行的真空获得方案以减小膜片被破坏的几率。
1. 剥离膜固定方式研究现状
国外散裂中子源对于剥离膜的快速安装方法进行了相关研究，除了美国散裂中子源(SNS)膜片采用单边无布丝悬挂固定方式外，大部分剥离膜固定方式均与图 1所示类似，即在膜架上布丝，以交叉的形式固定剥离膜，这种固定方式主要应用在J-PARC及LANL装置上。密集布丝能有效防止剥离膜边角因高温产生的起皱、弯曲等热应力释放现象，但是，这也是造成束流损失的一大原因。
由于散裂中子源环内循环质子束重复穿越，会在膜片上沉积大量的能量，产生很高的温度，同时在满足剥离效率要求下，一般选择熔点高、尽量薄的剥离膜片。所有类型剥离膜的共同特点是：(1)薄、易碎；(2)制备或安装困难；(3)耐高温。尽管选择的膜片材料都是高熔点的材料，但是交变的热载仍会使剥离膜褶皱、撕裂。另外，经测试，在室温环境下碳剥离膜在其变形量为12 mm时便破碎，如图 2所示。
2. 散裂中子源剥离膜批量安装试验
综合考虑束流包络、束流路径等因素，剥离膜采用双边固定形式[1-3]。由于膜片在重复注入次数为4次时温度将从300 K上升到1600 K，如图 3所示，膜片将承受热应力。碳膜采用双边固定及碳纤维辅助支撑方式，如图 4所示，能有效缓解剥离膜热变形[1-3]。
超薄剥离膜安装装置(如图 5所示)由底架、微距手动升降台、定位台面、碳纤维固定滚筒及标准定位块组成。装配过程首先将基底膜架安装在定位台面上，然后依次装配碳纤维和膜片，通过微距手动升降台抬高定位台面使碳纤维张紧，再装配支撑碳纤维，使用标准定位块对膜片进行高精度定位，最后安装夹紧膜架。整个过程需要在没有空气扰动、没有震动的环境下完成，严禁肢体接触膜片[4-6]。
图 5 碳膜辅助安装装置及批量安装样品Figure 5. Stripper foil installation set and the installation samples3. 剥离膜空气动力学分析
剥离膜系统需要在1×10-6 Pa的超高真空环境下工作，在真空获得阶段，气体流动将造成剥离膜震动或摆动，震动或摆动可能造成剥离膜片破坏，严重影响其寿命[5-6]。本文通过分析得出真空获得阶段真空抽速对膜片震动或摆动的影响，保证膜片使用寿命。剥离膜空气动力学分析采用Ansys的Workbench Fluent和Static Structural两模块进行。本文采用压差设定反推的方法获得膜片在不同进出口压力差的真空获得过程中的应力应变，对比膜片的允许应力应变获得进出口压差的限值。图 6为根据不同压差得出膜片的最大应力应变曲线图，膜片最大应力应变与压差成线性比例关系。从图 6中可见，进出口压差300 Pa以内，膜片形变在可承受范围内。
图 6 不同压差膜片最大应力应变分布图Figure 6. Maximum stress and strain distribution under different pressure difference图 7为300 Pa进出口压差计算残差值，进出口不平衡误差为0.006 5%，计算收敛。由于气体流动造成的膜片表面压力分布如图 8所示，膜片上所受压差为7 Pa左右。图 9为剥离膜系统空气流动分布图，在膜片周围，气体流动速度几乎为0。图 10为剥离膜周围空气扰动分布截面图，在膜片附近存在较小扰动，扰动压差大约为7 Pa。图 11为出口气流速度分布图，最高速度为23 m/s。图 12为膜片应力应变分布图，最大应变为0.012 m，最大应力为40 MPa。根据图 2实验，当膜片的摆动量超过12 mm时将造成破坏，因此可知，在压差低于300 Pa时，膜片的最大应力为4.02×107 Pa，膜片最大应变为12.2 mm，膜片可能受到破坏，因此真空获得时压差不得高于300 Pa。
4. 剥离膜系统真空获得测试
经Workbench fluent模拟分析计算，300 Pa压差时，出口端的速度为4.609 m/s，出口半径为0.03 m，则允许最大流速为13 L/s，由于前级泵抽速为8 L/s，低于理论计算的流速，因此在剥离膜系统真空获得的粗抽阶段，无需进行抽速限制。图 13为实际真空获得过程中，膜片的真实情况，据观察, 膜片未发生震动或摇摆。
剥离膜系统真空获得主要使用抽速为300 L/s的分子泵机组一套，前级泵粗抽抽速为8 L/s，采用MKS937B CCG真空计监测系统真空度。使用氦质谱检漏仪监测，系统漏率优于3.2×10-11 mbar·L/s，经调试，剥离膜系统最终真空度优于1.3×10-7 Pa，如图 14所示。
5. 结论
散裂中子源剥离膜超薄易碎的特点导致膜片安装及真空获得困难，本文通过研究设计了剥离膜片辅助安装装置，实现样品的批量安装；采用压差设定反推的分析方法，通过Fluent仿真获得膜片真空获得过程中的压力分布、膜片周围空气扰动、系统气体流动及膜片的应力应变分布情况，制定在不破坏剥离膜的前提下真空获得方案，通过实际测试，膜片完好并获得系统超高真空。
-
图 1 基于共轭SN的MC减方差方法流程图
Figure 1. Flowchart of MC variance reduction method based on adjoint SN
图 3 秦山一期堆芯中平面JSNT网格划分示意图
Figure 3. JSNT mesh for core mid-plane of phase Ⅰ of Qianshan Nuclear Power Plant
图 4 秦山一期前100万无偏和偏倚源粒子分布示意图
Figure 4. First million unbiased and biased source particles for phase Ⅰ of Qianshan Nuclear Power Plant
图 5 CAP1400压力容器内表面快中子注量率JMCT和JSNT计算模型示意图
Figure 5. JMCT and JSNT models for CAP1400 RPV calculation
图 6 CAP1400压力容器内表面JSNT共轭源和JMCT前100万源粒子示意图
Figure 6. Adjoint source of JSNT and first million biased source particles of JMCT
图 7 CAP1400压力容器内表面快中子注量率(E≥1.0 MeV)分布
Figure 7. FNFR distribution (E≥1.0 MeV) on inner RPV of CAP1400
图 8 CAP1400堆腔剂量率JMCT和JSNT计算模型示意图
Figure 8. JMCT and JSNT models for CAP1400 cavity dose rate calculation
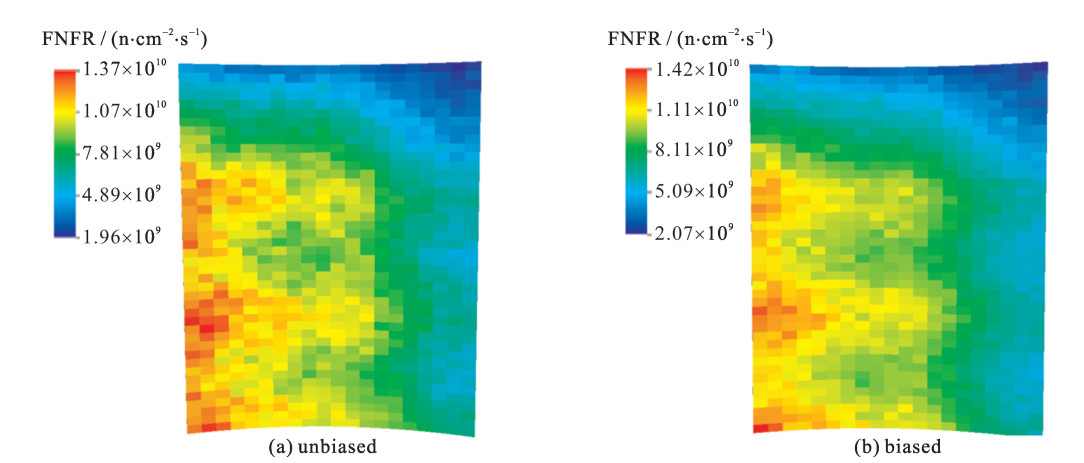
表 1 秦山一期快中子注量率(E≥1.0 MeV)计数误差小于0.05时计算总时间和加速比
Table 1. Calculation time and speedup for different cases with fast neutron fluence rate (FNFR) tally error less than 0.05
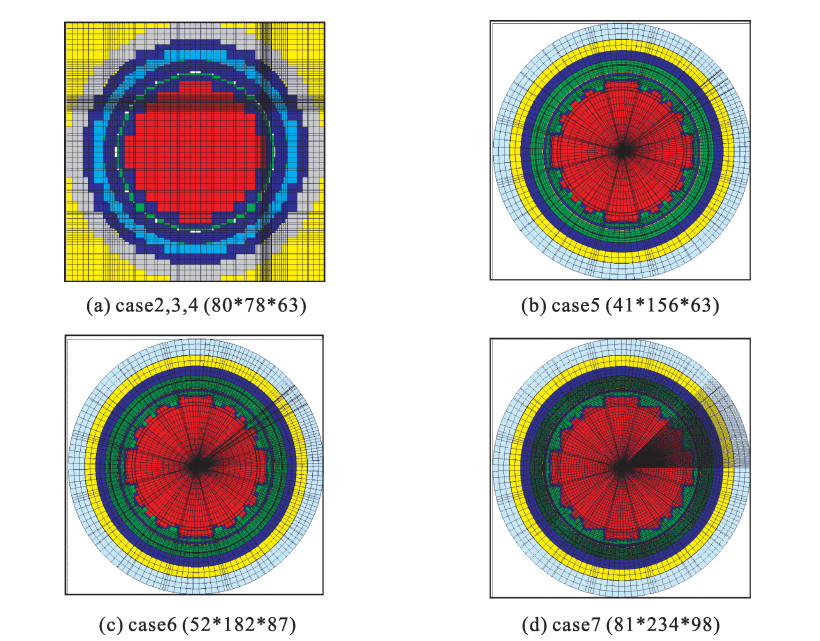
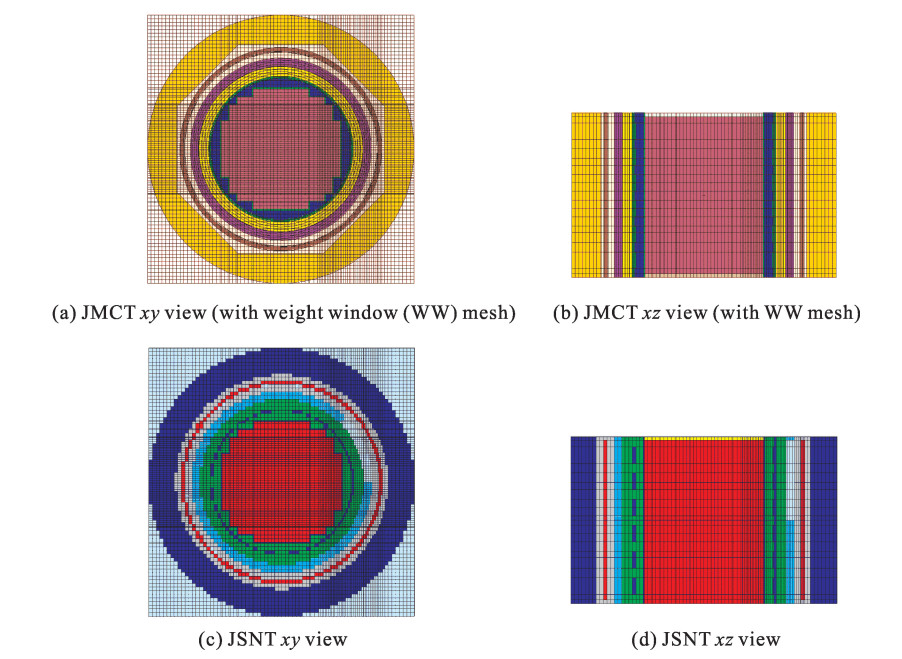
case geometry type number of mesh fast neutron fluence rate/(109 n·cm-2·s-1) JSNT time/min JMCT time/min total time T/min speedup (T_bias/ T_unbias) measure - - 7.41 - - - - 1(unbiased) - - 6.08 - 19 814.12 19 814.12 1 2 xyz 393 120 6.48 19.66 3 575.56 3 595.22 6 3 xyz 393 120 6.35 19.66 197.92 217.58 91 4 xyz 393 120 6.41 19.66 30.00 49.66 399 5 rtz 402 948 5.92 80.83 100.78 181.61 109 6 rtz 823 368 6.44 161.66 429.62 591.28 34 7 rtz 1 857 492 6.53 397.59 185.07 582.66 34 
下载: 导出CSV
表 2 CAP1400压力容器内表面快中子注量率各个计数误差区间内的网格数目
Table 2. Number of mesh in each tally error bin on inner RPV of CAP1400
tally error number of mesh upper lower unbiased biased 0.00 0.01 0 0 0.01 0.02 0 1 0.02 0.03 0 311 0.03 0.04 0 350 0.04 0.05 343 119 0.05 0.06 322 48 0.06 0.07 114 16 0.07 0.08 50 8 0.08 0.09 21 1 0.09 0.10 7 1 0.10 1.00 3 5
下载: 导出CSV
表 3 CAP1400堆腔剂量率中子和光子剂量率及加速比
Table 3. Neutron dose rate, photon dose rate and speedup for CAP1400 cavity dose rate calculation
dose rate/(mSv·h-1) tally error/10-2 sum of time/min M/10-2 JMCT speedup(M_biased/M_ref) case1: particle type neutron 2.82×106 7.14 10 612.57 1.85 1 biased source (reference) photon 6.82×104 5.35 10 612.57 3.29 1 case2: neutron and photon neutron 2.80×106 1.30 10 384.53 57 31 fluence rate response function photon 6.50×104 3.15 10 384.53 9.70 3 case3: neutron and photon neutron 2.82×106 1.15 10 064.27 75.1 41 dose rate response function photon 6.27×104 1.74 10 064.27 32.8 10
下载: 导出CSV
-
[1] Wagner J C. Acceleration of Monte Carlo shielding calculations with an automated variance reduction technique and parallel processing[R]. University Park, 1997. [2] Wagner J C, Haghighat A. Automated variance reduction of Monte Carlo shielding calculations using the discrete ordinates adjoint function[J]. Nuclear Science and Engineering, 1998, 128: 186-208. doi: 10.13182/NSE98-2 [3] Haghighat A, Wagner J C. Monte Carlo variance reduction with deterministic importance functions[J]. Progress in Nuclear Energy, 2003, 42(1): 25-53. doi: 10.1016/S0149-1970(02)00002-1 [4] Blakeman E D, Peplow D E, Wagner J C, et al. PWR facility dose modeling using MCNP5 and the CADIS/ADVANTG variance-reduction methodology[R]. ORNL/TM-2007/133, 2007. [5] Peplow D E, Evans T M, Wagner J C. Simultaneous optimization of tallies in difficult shielding problems[J]. Nuclear Technology, 2008, 168: 785-792. [6] Wagner J C, Peplow P E, Evans T M. Automated variance reduction applied to nuclear well-logging problems[J]. Nuclear Technology, 2009, 168: 799-809. doi: 10.13182/NT09-A9309 [7] Vasiliev A, Ferroukhi H, Zimmermann M A, et al. Development of a CASMO-4/SIMULATE-3/MCNPX calculation scheme for PWR fast neutron fluence analysis and validation against RPV scraping test data[J]. Annals of Nuclear Energy, 2007, 34: 615-627. doi: 10.1016/j.anucene.2007.02.020 [8] Fero A H. SORCERY user manual[R]. LTR- R EA-06-74, 2006. [9] X-5 Monte Carlo Team, MCNP - Ageneral Monte Carlo N-Particle transport code[R]. LA-UR-03-1987, 2003. 期刊类型引用(1)
1. 刘欢, 唐曌堃. 基于计算机视觉的易碎产品包装检测系统设计. 自动化与仪器仪表. 2019(12): 30-33 . 
百度学术其他类型引用(0)
-
下载:
点击查看大图
计量
- 文章访问数: 939
- HTML全文浏览量: 206
- PDF下载量: 91
- 被引次数: 1
