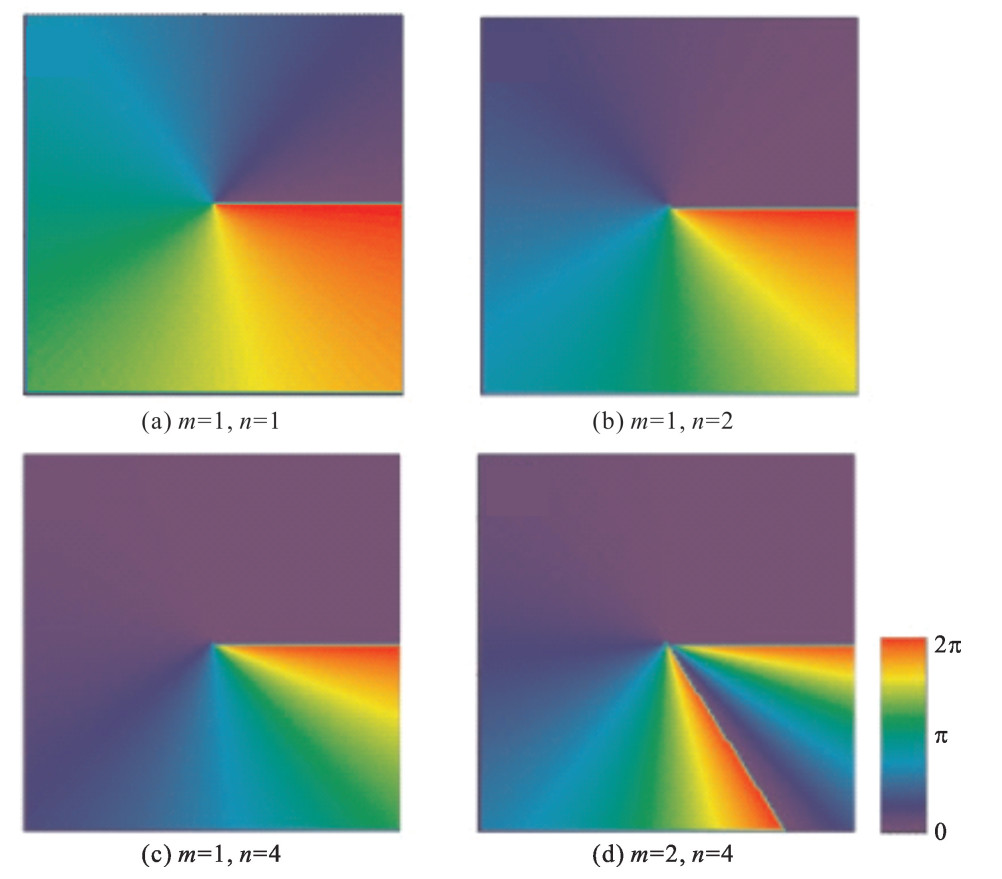
Focusing properties of power-exponent-phase vortex beam focused by high numerical-aperture objective
-
摘要: 为了获得多种类型的波长量级聚焦光斑，研究了一种新型涡旋光束，高次方涡旋光束经过大数值孔径透镜的聚焦。基于矢量德拜积分公式，理论上研究了线偏振的高次方涡旋光束经过大数值孔径透镜的聚焦特性。研究了涡旋光束的拓扑荷数和幂次方数对聚焦平面光强和电场x分量的相位分布的影响。研究结果表明，通过控制涡旋光束的拓扑荷数和幂次方数可以产生不同类型的聚焦光强分布，例如尺寸约为2个波长大小的实心和空心型聚焦光斑。此外，与普通的涡旋光束聚焦不同，高次方涡旋光束聚焦后的奇点并不在焦点处。这些特殊的聚焦光斑有望在微粒的操控等领域中得到应用。Abstract: Based on vectorial Debye theory, the focusing properties of linearly polarized power-exponent-phase vortex beam focused by a high numerical aperture objective is studied. The influence of the topological charge and power index on the focal intensity and the phase of x-component is investigated in detail. The result shows that different types of focal intensity distribution, such as dark-core shape focal beam with beam size of 2 wavelength, can be generated by controlling the topological charge and power index. In particular, it is found that the phase singularity of power-exponent phase vortex beam has a deviation from the geometrical focus. The potential applications of this study may include particle manipulation.
-
Key words:
- vortex beam /
- high numerical aperture /
- tight focusing /
- phase singularity
-
图 1 大数值孔径聚焦示意图
Figure 1. Schematic diagram of focusing of beams by high numerical-aperture objective
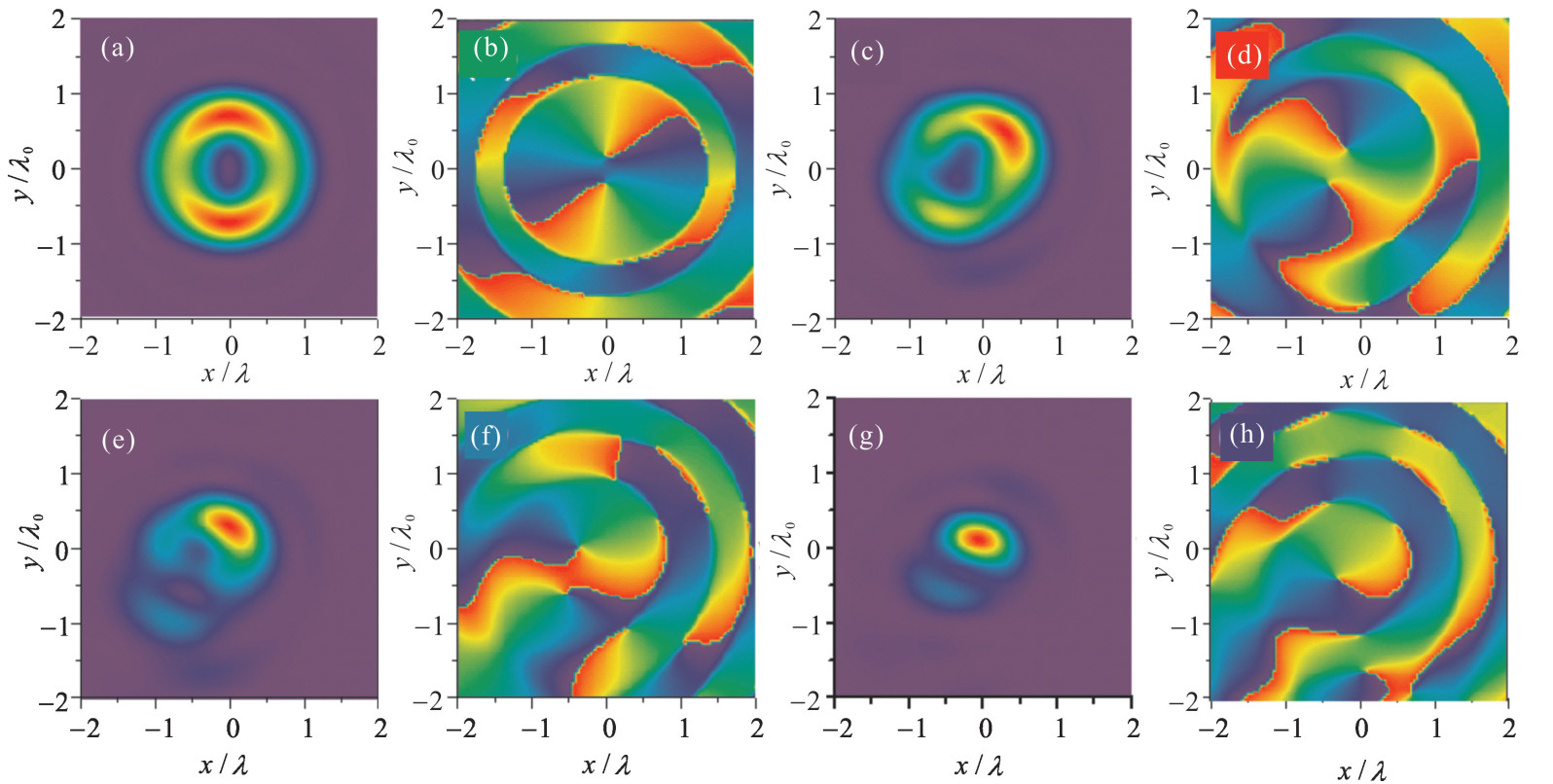
图 3 拓扑荷数为1的涡旋光束经过大数值孔径透镜聚焦的总光强(a, c, e, g)及x分量的相位(b, d, f, h)。光束的幂次方分别为(a, b): n=1; (c, d): n=2; (e, f): n＝4; (g, h): n=10
Figure 3. Total intensity (a, c, e, g) and phase of x-component (b, d, f, h) of vortex beams with m=1 focused by a high numerical aperture objective. (a, b): n=1; (c, d): n=2; (e, f): n＝4; (g, h): n=10
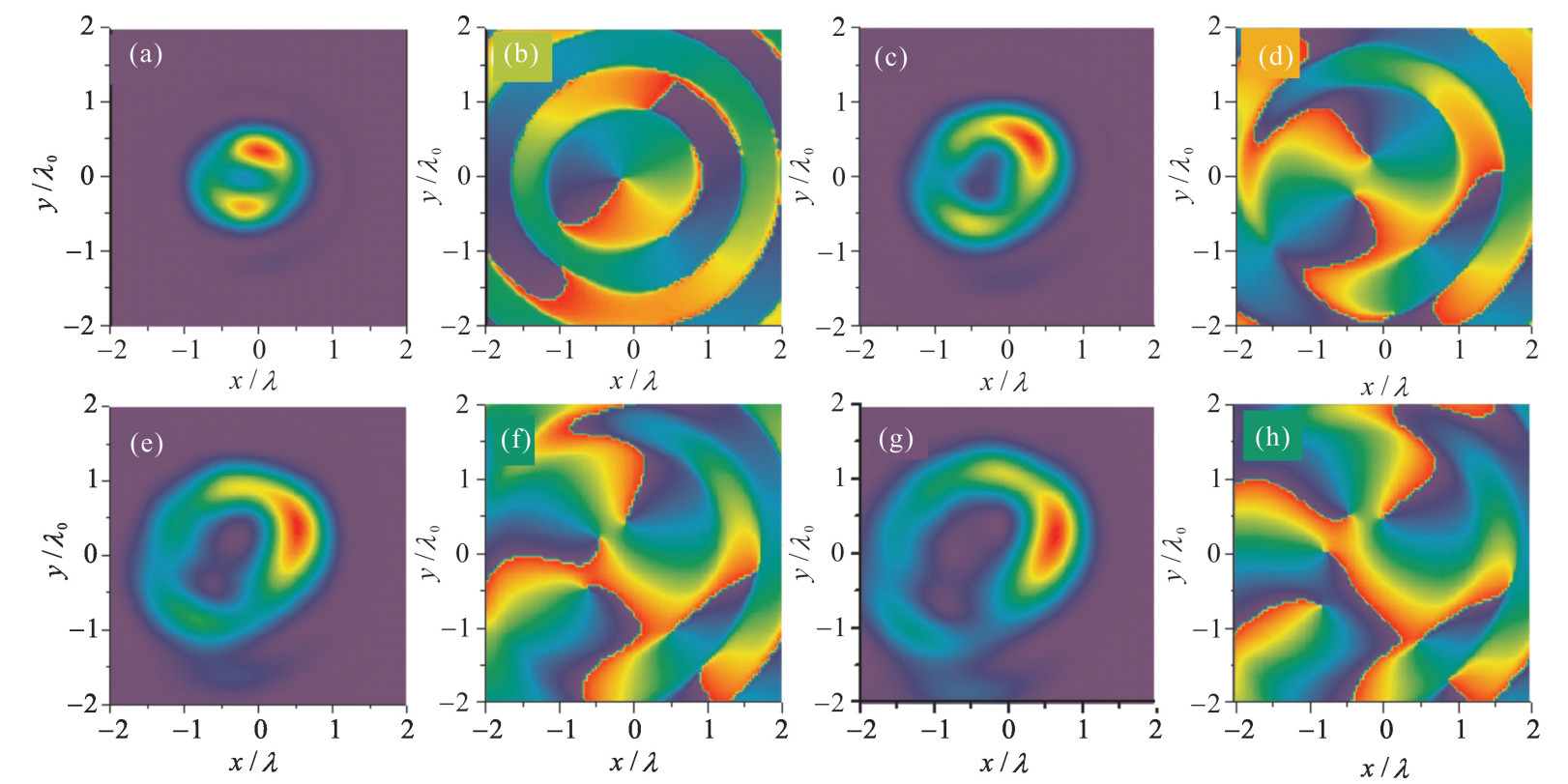
图 4 拓扑荷数为2的涡旋光束经过大数值孔径透镜聚焦的总光强(a, c, e, g)及x分量的相位(b, d, f, h)。光束的幂次方分别为(a, b): n=1; (c, d): n=2; (e, f): n＝4；(g，h): n=10
Figure 4. Total intensity (a, c, e, g) and phase of x-component (b, d, f, h) of vortex beams with m=2 focused by a high numerical aperture objective. (a, b): n=1; (c, d): n=2; (e, f): n＝4; (g, h): n=10
图 5 二次方涡旋光束经过大数值孔径透镜聚焦的总光强(a, c, e, g)及x分量的相位(b, d, f, h)。光束的拓扑荷数分别为(a, b): m=1; (c, d): m=2; (e, f): m＝3; (g, h): m=4
Figure 5. Total intensity (a, c, e, g) and phase of x-component (b, d, f, h) of vortex beams with n=2 focused by a high numerical aperture objective. (a, b): m=1; (c, d): m=2; (e, f): m＝3; (g, h): m=4
-
[1] Gu M. Advanced optical imaging theory[M]. Berlin: Springer Heidelberg, 1999. [2] Wang H, Shi L, Lukyanchuk B, et al. Creation of a needle of longitudinally polarized light in vacuum using binary optics[J]. Nature Photonics, 2008, 2(8): 501-505. doi: 10.1038/nphoton.2008.127 [3] Yan S, Yao B, Rupp R, et al. Shifting the spherical focus of a 4Pi focusing system[J]. Optics Express, 2011, 19(2): 673-678. doi: 10.1364/OE.19.000673 [4] 罗亚梅, 高曾辉, 唐碧华, 等. 聚焦高斯涡旋光束焦区电场和磁场的偏振奇点[J]. 物理学报, 2014, 63: 154201. doi: 10.7498/aps.63.154201Luo Yamei, Gao Zenghui, Tang Bihua, et al. Electric and magnetic polarization singularities of focused Gaussian vortex beams in the focal region. Acta Physica Sinica, 2014, 63: 154201 doi: 10.7498/aps.63.154201 [5] Liu Z, Jones P H. Optical manipulation using highly focused alternate radially and azimuthally polarized beams modulated by a devil's lens[J]. J Opt Soc Am A, 2016, 33(12): 2501-2508. doi: 10.1364/JOSAA.33.002501 [6] Neugebauer M, Aiello A, Banzer P, et al. Linear and angular momenta in tightly focused vortex segmented beams of light[J]. Chin Opt Lett, 2017, 15: 030003. doi: 10.3788/COL201715.030003 [7] Liu Z, Zhao D. Radiation forces acting on a Rayleigh dielectric sphere produced by highly focused elegant Hermite-cosine-Gaussian beams[J]. Optics Express, 2012, 20(3): 2895-2904. doi: 10.1364/OE.20.002895 [8] Allen L, Beijersbergen M W, Spreeuw R J, et al. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes[J]. Phys Rev A, 1992, 45(11): 8185-8189. doi: 10.1103/PhysRevA.45.8185 [9] Zhang Jianbin, Pang Zihao, Feng Liyan, et al. Propagation properties of the chirped Airy vortex beams through left-handed and right-handed material slabs[J]. Chin Opt Lett, 2017, 15: 060501. doi: 10.3788/COL201715.060501 [10] Fu Shiyao, Wang Tonglu, Gao Yan, et al. Diagnostics of the topological charge of optical vortex by a phase-diffractive element[J]. Chin Opt Lett, 2016, 14: 080501. doi: 10.3788/COL201614.080501 [11] Janet C A P, Rajesh K B, Udhayakumar M, et al. Tight focusing properties of radially polarized Gaussian beams with pair of vortices[J]. Chin Opt Lett, 2016, 33: 124206. [12] Lao G, Zhang Z, Zhao D, et al. Propagation of the power-exponent-phase vortex beam in paraxial ABCD system[J]. Opt Exp, 2016, 24(16): 18082-18094. doi: 10.1364/OE.24.018082 [13] Richards B, Wolf E. Electromagnetic diffraction in optical systemsⅡ. Structure of the image field in an aplanatic system[J]. Proc R Soc A, 1959, 253: 358-379. -
下载:
点击查看大图
计量
- 文章访问数: 1987
- HTML全文浏览量: 550
- PDF下载量: 467
- 被引次数: 0
