电磁发射装置轨道热管理冷却管道的力学设计

林灵淑; 袁伟群; 赵莹; 王志增; 严萍

doi:10.11884/HPLPB201830.170322

电磁发射装置轨道热管理冷却管道的力学设计

doi: 10.11884/HPLPB201830.170322

林灵淑^{1, 2,},
袁伟群²,
赵莹²,
王志增²,
严萍^{2, 3, ,}

1.
中国科学院大学, 北京 100190
2.
中国科学院电工研究所, 北京 100190
3.
中国科学院电力电子与电力驱动重点实验室, 北京 100190

基金项目:

国家自然科学基金项目 51237007

国家自然科学基金项目 51207178

详细信息

作者简介:
林灵淑(1991—)，女，博士研究生，主要从事脉冲功率技术的研究；linlingshu13@mail.iee.ac.cn

通讯作者:
严萍(1966—)，女，博士，研究员，主要从事高电压绝缘技术和脉冲大电流放电技术的研究；pingyan@mail.iee.ac.cn

中图分类号: TM89
计量
- 文章访问数: 1165
- HTML全文浏览量: 329
- PDF下载量: 175
- 被引次数: 0
出版历程
- 收稿日期: 2017-08-25
- 修回日期: 2017-10-23
- 刊出日期: 2018-02-15

Mechanical design of rail cooling pipe for electromagnetic launcher

Lin Lingshu^{1, 2
,},
Yuan Weiqun²,
Zhao Ying²,
Wang Zhizeng²,
Yan Ping^{2, 3
, ,}

1.
University of Chinese Academy of Sciences, Beijing 100190, China
2.
Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China
3.
Key Laboratory of Power Electronics and Electric Drive, Chinese Academy of Sciences, Beijing 100190, China

摘要

摘要: 为了解决电磁轨道发射器在实际应用中遇到的高热量积累问题，需要对轨道进行冷却。基于多物理场耦合仿真平台Comsol Multiphysics，从轨道结构特性和电气特性两个方面进行分析，提出了在轨道内部设置冷却管道的基本规律。建立发射器的电磁场和结构场耦合模型，利用有限元法对预紧力和电动力作用下的轨道响应进行数值计算。仿真结果表明，设置冷却管道会对轨道造成材料损失，进而影响轨道性能，冷却管道应当尽可能远离肩部与枢-轨接触面连接处，并提出了冷却管道位于轨道不同位置时，轨道的形变规律和电感梯度变化规律，为轨道热管理冷却管道的设置方案提供了理论依据。
- 电磁发射 /
- 热管理 /
- 轨道冷却 /
- 电感梯度 /
- 形变
Abstract: In order to solve the high quantity of heat accumulation problems of the electromagnetic rail launcher, the rail cooling is necessary. This paper presents the basic principles for setting cooling pipes inside the rail from two aspects of mechanical performance and electrical performance analysis.An electromagnetic field and structure field model is established, the finite element method is used for numerical calculation of rail's response to the pre-tightening force and the eletromagnetic force. Simulation results show that, the cooling pipe will cause material damage, which has negative influence on rail performance; the cooling pipe should be set as far as possible away from the shoulder and armature-rail interface connection. This paper also puts forward the laws of rail deformation and inductance gradient with cooling pipe in different locations.
- electromagnetic launcher /
- thermal management /
- rail cooling /
- inductance gradient /
- deformation

HTML全文

惯性约束聚变(ICF)^[1-4]的目标是约束氘氚聚变燃料并点火，实现可控核聚变反应并产生可观的能量。激光间接驱动^[5-6]是目前最流行的方式之一。将激光注入装有氘氚燃料靶丸的金或铀黑腔中转换为X射线辐射，辐射均匀地辐照到靶丸上，烧蚀驱动靶丸内爆实现氘氚燃料的高密度压缩，并在靶丸芯部产生高温热斑，达到热核点火条件，并且在燃料飞散前充分燃烧、产生足够的聚变能量。2018年美国劳伦斯利弗莫尔国家实验室(LLNL)在国家点火装置(NIF)^[7]上实现了聚变能输出大于内爆动能的实验^[8]。我国2016年实现了间接驱动内爆集成实验^[9]，2018年在黑腔中进行了内爆实验^[10]。激光聚变间接驱动目前的研究难点是控制黑腔内的激光等离子体不稳定性(LPI)、控制内爆中的流体力学不稳定性以及解决内爆混合^[11-14]的问题。黑腔中靶丸加持膜^[15]和充气管引起的不稳定性^[16]也限制了内爆压缩达到高增益点火条件。

直接数值模拟是点火靶物理研究与设计的重要手段，为此美国发展了LASNEX^[5], HYDRA^[17]等辐射流体力学模拟程序，我国也发展了系列辐射流体力学程序^[18]。这些程序物理建模复杂、代码量庞大、网络分辨率高，具有较高的模拟置信度。然而，对数值模拟的过多依赖导致ICF内爆过程中的基本物理机制无法简明扼要地获得，不利于系统地分析内爆过程中影响靶丸能量增益的基本物理机制和规律。

本文的工作是用定标方法建立简单、易懂的内爆动力学模型，分析影响内爆和能量增益的基本物理机制，在物理规律上研究设计参数对靶丸性能的影响。内爆加速阶段使用火箭模型^{[1, 2, 19]}描述，减速阶段依靠劳森判据和定标律^[20]描述，热斑形成与点火采用一维流体力学开源程序MULTI-IFE^[21]辅助定标。由此获得靶丸设计所需的参数空间，研究参数空间在不同初始条件下的变化规律。在一定的靶丸性能要求下，给出了靶丸基本的设计参数范围。当改变靶丸的驱动辐射温度、飞行熵增因子、整形速度和烧蚀体材料的条件下，靶丸的装量、半径以及壳层厚度应当作相应地调整。

1. 理论模型

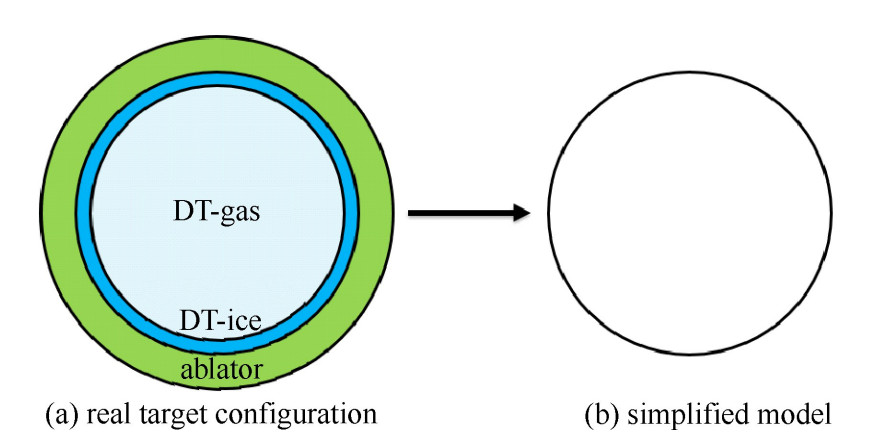
如图 1(a)所示，实际的间接驱动点火靶丸由同心的球型壳层组成。壳层分为外层烧蚀体和内层主燃料两部分。外层烧蚀体由聚苯乙烯塑料(CH)或金属铍(Be)等低原子序数物质制成，为了防止预热、控制流体力学不稳定性等，烧蚀体一般由不同的掺杂层构成，掺杂的元素有硅、锗、钨等。内层主燃料为冷冻氘氚(DT-ice)固体。壳层内部的空腔中充满稀薄的氘氚蒸汽(DT-gas)。壳层厚度比靶丸半径小很多，经过整形驱动压缩后，壳层变得更薄，因此靶丸壳层可以假设成一个具有初始装量M₀且位置在R₀处的薄壳，如图 1(b)所示。在薄壳假设的基础上，1.1至1.3部分分阶段对靶丸内爆过程进行物理建模。

图 1 实际靶丸构型与简化模型

Figure 1. The real target configuration and the simplified model

下载: 全尺寸图片幻灯片

1.1 加速阶段

当靶丸受到辐射烧蚀时，壳层的一部分烧蚀体向外喷射，反作用力推动壳层聚心内爆。辐射对靶丸壳层产生的质量烧蚀速率和烧蚀压为 $\dot m$ =aT_r³，p_a=bT_r^3.5，其中 $\dot m$ 的单位是g·cm^-2·μs，p_a的单位是Mbar，辐射温度T_r的单位是heV。烧蚀定标律系数a, b由烧蚀体的材料决定：(1)文献[5]式(6-2)(6-3)给出了CH的烧蚀定标律系数；(2)文献[22]给出了Ge-doped CH、HDC和Cu-doped Be的质量烧蚀速率与辐射温度之间的实验数据图并拟合其数据给出这三种材料的系数a；文献[22]也给出了HDC和Cu-doped Be的烧蚀压与辐射温度之间的数据图，拟合可得b_HDC=5;b_Be=6.31，但是未给出Ge-doped CH烧蚀压数据。为了方便计算和讨论，我们假设有b/a=10。由此获得表 1中的数据。

表 1 不同材料的烧蚀定标律系数

Table 1. The parameters for different ablator materials

materials	a/(g·cm^-2·μs·heV^-3)	b/(Mbar·heV^-3.5)
CH	0.30	3.0
Ge-doped CH	0.35	3.5
HDC	0.50	5.0
Cu-doped Be	0.75	7.5

下载: 导出CSV

| 显示表格

驱动壳层内爆的辐射由整形脉冲和主脉冲两部分构成。本文从主脉冲驱动的加速阶段开始研究，假设整形脉冲结束后，壳层获得初始内爆速度为v₀。壳层的初始半径位置设为R₀，壳层的初始装量(包括烧蚀层和DT主燃料)设为M₀。随后，辐射主脉冲烧蚀靶丸壳层并驱动其加速内爆，根据质量守恒、牛顿第二定律可得^[19]

$\left\{\begin{array}{l} \frac{\mathrm{d} M(t)}{\mathrm{d} t}=-4 {\rm{ \mathsf{ π} }} R^2(t) \dot{m} \\ M(t) \frac{\mathrm{d} v(t)}{\mathrm{d} t}=4 {\rm{ \mathsf{ π} }} R^2(t) p_{\mathrm{a}} \\ \frac{\mathrm{d} R(t)}{\mathrm{d} t}=-v(t) \end{array}\right.$

(1)

由式(1)有dv(t)=-(p_a/ $\dot m$ )(dM(t)/M(t))，对其积分可得加速到t时刻的内爆速度v=v₀+(p_a/ $\dot m$ )ln(1/δ_t)。物理上，随着壳层向内聚心，靶丸体积逐渐变小，内部气体压力逐步上升，当内部气体压力等于靶丸驱动压力时，靶丸壳层获得最大内爆速度，之后壳层开始减速。最大内爆速度时刻，记壳层剩余质量份额为δ=m_s/M₀，其中m_s为剩余壳层质量，则最大的内爆速度为v_imp=v₀+(p_a/ $\dot m$ )ln(1/δ)。

仍由式(1)得

$C_0(1-\delta)+\delta \ln \delta=\frac{\dot{m}^2}{p_{\mathrm{a}} M_0} \frac{4 {\rm{ \mathsf{ π} }}}{3} R_0^3=D_0 ; \quad C_0=v_0 \frac{\dot{m}}{p_{\mathrm{a}}}+1$

(2)

用初始参量表达最大内爆速度有v_imp=v₀-10lnδT_r^0.5=v₀δ^-1+[10T_r^0.5(δ^-1-1)-( $\dot m$ /M₀)(4π/3)R₀³δ^-1]。进一步简化计算，将此加速过程近似为均加速的，使用v≈(v₀+v_imp)/2可得壳层的加速时间τ=R₀/v=R₀/(v₀-5lnδT_r^0.5)和平均加速度g=2(R₀-v₀τ)/τ²=10(5lnδT_r^0.5-v₀)lnδT_r^0.5/R₀。

假设加速过程中密度为常数，壳层压力等于烧蚀压，加速过程飞行熵增因子为α_if，可得壳层密度为ρ=[p_a/(α_ifA_deg)]^3/5=A_deg^-0.6b^0.6α_if^-0.6T_r^2.1，其中A_deg=2.17×10¹² (erg/cm³)/(g/cm³)^5/3是氘氚固体的特征常数^[2]。壳层的初始厚度为ΔR₀=M₀/(ρ4πR₀²)=(4π)^-1A_deg^0.6b^-0.6α_if^0.6T_r^-2.1M₀R₀^-2，靶丸的初始形状因子为A_r0=R₀/ΔR₀=(4π)¹A_deg^-0.6b^0.6α_if^-0.6T_r^2.1M₀^-1R₀³。

在靶丸加速过程中，烧蚀面上压力梯度和密度梯度反向，引发烧蚀瑞利—泰勒不稳定性^[23](A-RTI)增长，此时界面附近的物理量可表示为 $f(x, y ; t)=f_0(x)+\sum\limits_k f_k(x) \mathrm{e}^{\mathrm{i} k y} \mathrm{e}^{\gamma_t t}$ ，其中

$\gamma_1=0.9 \sqrt{\frac{k_1 g}{1+k_1 L}}-1.4 k_1 v_{\mathrm{a}}$

(3)

是A-RTI线性增长率^[24-25]。不稳定性增长率由RT增长项 $0.9 \sqrt{k_1 g /\left(1+k_1 L\right)}$ 和烧蚀致稳项-1.4k_lv_a组成，其中波数为k_l=2π/λ=l/R=2lR₀^-1; R=R₀/2。式(3)中L表示密度梯度标长^[24]，本文用辐射自由程^[2]来近似，即L=ρ/(dρ/dr)=1/(κ_pρ)，其中κ_p=0.43(Z³/A²)ρT_r^-7/2=0.43Z³A^-2A_deg^-0.6b^0.6α_if^-0.6T_r^-1.4表示辐射的平均光厚^[2]。烧蚀致稳项中的烧蚀速度可定义为

$v_{\mathrm{a}}=\frac{M_0(1-\delta)}{4 {\rm{ \mathsf{ π} }} \rho\left(\frac{3}{4} R_0\right)^2 \tau}=\frac{4}{9 {\rm{ \mathsf{ π} }}} A_{\mathrm{deg}}^{0.6}\left(v_0-5 \ln \delta T_{\mathrm{r}}^{0.5}\right)(1-\delta) b^{-0.6} \alpha_{\mathrm{if}}^{0.6} T_{\mathrm{r}}^{-2.1} M_0 R_0^{-4}$

(4)

这里近似加速阶段壳层的表面积从4πR₀²收缩到0，故v_a中有R=3R₀/4。A-RTI发展的时间就是壳层加速内爆的时间τ。则A-RTI线性增长的指数因子为

$\begin{array}{r} \gamma_l \tau=0.9 \sqrt{\frac{4 l}{1+4.65 l Z^{-3} A^2 A_{\mathrm{deg}}^{1.2} b^{-1.2} \alpha_{\mathrm{if}}^{1.2} T_{\mathrm{r}}^{-0.7} R_0^{-1}} \frac{5 \ln \delta T_{\mathrm{r}}^{0.5}}{\left(5 \ln \delta T_{\mathrm{r}}^{0.5}-v_0\right)}}- \\ 0.396 l A_{\mathrm{deg}}^{0.6}(1-\delta) b^{-0.6} \alpha_{\mathrm{if}}^{0.6} T_{\mathrm{r}}^{-2.1} M_0 R_0^{-4} \end{array}$

(5)

l模扰动线性增长的放大倍数为G_{f_l}=e^γ_lτ，记G_f为l=1~100阶模放大倍数的最大值。设计上要求A-RTI的幅值不超过壳层厚度，则所容忍的最大初始扰动幅值可以近似为η=ΔR₀/G_f。

1.2 减速阶段

减速过程^{[19, 26]}中，壳层对气体做功，内部气体的压力和能量升高，壳层的动能减小。当壳层动能消耗殆尽时，达到阻滞时刻，之后靶丸开始向外飞散。阻滞时刻，壳层的熵增因子记为α_s(称为阻滞熵增因子)，其与飞行熵增因子的关系为 $\alpha_{\mathrm{s}}=\alpha_{\mathrm{if}} \sqrt{M}=\alpha_{\mathrm{if}}^{0.85} v_{\mathrm{imp}}^{0.5} p_{\mathrm{a}}^{-0.1} \gamma^{-0.25} A_{\mathrm{deg}}^{-0.15}$ ，其中 $M=v_{\mathrm{imp}} / c_{\mathrm{if}}=v_{\mathrm{imp}} / \sqrt{\gamma p_{\mathrm{a}} / \rho}$ 是最大内爆速度时刻的马赫数^{[26, 27]}，c_if是最大内爆速度时刻壳层的声速。又记阻滞时刻靶丸的半径为r_s、壳层的密度和压力分别为ρ_s和p。并且我们假设阻滞时刻：(1)壳层和热斑等压，热斑的质量可忽略；(2)壳层压力可用阻滞熵增因子与壳层密度表达；(3)用理想气体的内能描述壳层的内能。我们还假设最大内爆速度时刻壳层的动能可以全部转化为阻滞时刻壳层的内能。由这些假设可得

$\left\{\begin{array}{l} m_{\mathrm{s}}=\frac{4 {\rm{ \mathsf{ π} }}}{3} r_{\mathrm{s}}^3 \rho_{\mathrm{s}} \\ p=\alpha_{\mathrm{s}} A_{\mathrm{deg}} \rho_{\mathrm{s}}^{5 / 3} \\ \frac{4 {\rm{ \mathsf{ π} }}}{3} r_{\mathrm{s}}^3 \frac{p}{\gamma-1}=\frac{1}{2} m_{\mathrm{s}} v_{\mathrm{imp}}^2 \end{array}\right.$

(6)

化简后有

$\left\{\begin{array}{l} p=\left(\frac{\gamma-1}{2}\right)^{5 / 2} v_{\mathrm{imp}}^5 \alpha_{\mathrm{s}}^{-3 / 2} A_{\mathrm{deg}}^{-3 / 2} \\ \rho_{\mathrm{s}}=\left(\frac{\gamma-1}{2}\right)^{3 / 2} v_{\mathrm{imp}}^3 \alpha_{\mathrm{s}}^{-3 / 2} A_{\mathrm{deg}}^{-3 / 2} \\ r_{\mathrm{s}}=\left(\frac{4 {\rm{ \mathsf{ π} }}}{3}\right)^{-1 / 3}\left(\frac{\gamma-1}{2}\right)^{-1 / 2} m_{\mathrm{s}}^{1 / 3} v_{\mathrm{imp}}^{-1} \alpha_{\mathrm{s}}^{1 / 2} A_{\mathrm{deg}}^{1 / 2} \end{array}\right.$

(7)

再将阻滞熵增α_s换为飞行熵增α_if，可得

$\left\{\begin{array}{l} p=\left(\frac{\gamma-1}{2}\right)^{2.5} \gamma^{0.375} A_{\mathrm{deg}}^{-1.275} v_{\mathrm{imp}}^{4.25} \alpha_{\mathrm{if}}^{-1.275} p_{\mathrm{a}}^{0.15} \\ \rho_{\mathrm{s}}=\left(\frac{\gamma-1}{2}\right)^{1.5} \gamma^{0.375} A_{\mathrm{deg}}^{-1.275} v_{\mathrm{imp}}^{2.25} \alpha_{\mathrm{if}}^{-1.275} p_{\mathrm{a}}^{0.15} \\ r_{\mathrm{s}}=\left(\frac{4 {\rm{ \mathsf{ π} }}}{3}\right)^{-1 / 3}\left(\frac{\gamma-1}{2}\right)^{-0.5} \gamma^{-0.125} A_{\mathrm{deg}}^{0.425} m_{\mathrm{s}}^{1 / 3} v_{\mathrm{imp}}^{-0.75} \alpha_{\mathrm{if}}^{0.425} p_{\mathrm{a}}^{-0.05} \end{array}\right.$

(8)

所以，我们获得了壳层内爆到阻滞时刻的物理量p, ρ_s, r_s, α_s对于最大内爆速度时刻的物理量m_s, v_imp, α_if, p_a和常数A_deg, γ的定标律。

1.3 聚变点火与燃烧

在理想情况下，阻滞或阻滞时刻之前，壳层内部(即靶丸中心)已形成点火热斑，引发聚变点火与燃烧。这样的燃烧从中心热斑开始，逐渐向外传播并引燃DT燃料壳层，进而引发所有的燃料燃烧。对于燃烧中的DT燃料等离子体，热斑和壳层等压且有均匀的压强p，此时约束热斑和壳层等离子体的是物质惯性。随后，这团等离子体将以稀疏波的形式向外膨胀，膨胀速度为阻滞时刻的声速c_s，则惯性约束时间^[4]可表示为

$\tau_{\mathrm{c}}=\frac{r_{\mathrm{s}}}{c_{\mathrm{s}}}=\frac{r_{\mathrm{s}}}{\sqrt{\gamma p / \rho_{\mathrm{s}}}}$

(9)

用最大内爆速度时刻的物理量表示它，得到

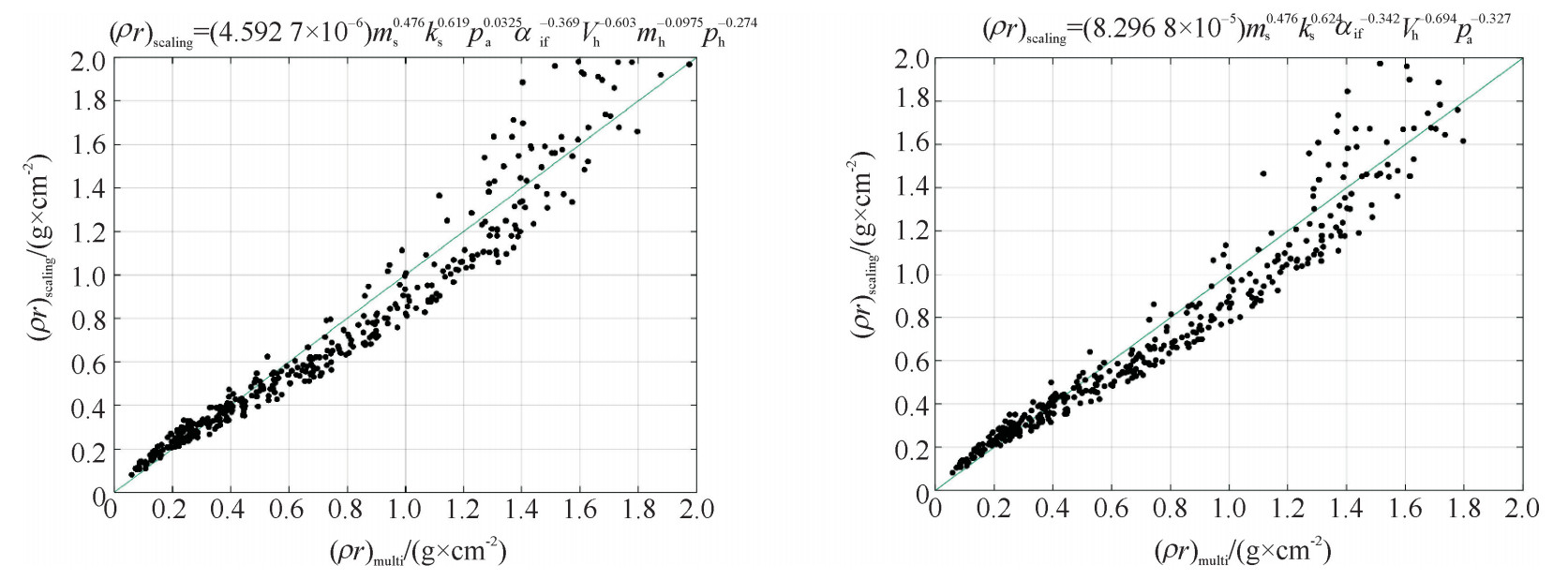
$\tau_{\mathrm{c}}=\left(\frac{4 {\rm{ \mathsf{ π} }}}{3}\right)^{-1 / 3}\left(\frac{\gamma-1}{2}\right)^{-1} \gamma^{-0.625} A_{\mathrm{deg}}^{0.425} m_{\mathrm{s}}^{1 / 3} v_{\mathrm{imp}}^{-1.75} \alpha_{\mathrm{if}}^{0.425} p_{\mathrm{a}}^{-0.05}$

(10)

我们需要进一步描述靶丸燃烧后的聚变反应产能和能量增益，这需要知道中心热斑和燃料壳层的总面密度。对于一个聚变点火并燃烧的靶丸，要求中心点火热斑的面密度(ρr)_h＞0.3 g/cm²、离子温度T_h＞4 keV且燃料壳层的面密度(ρr)_s＞1 g/cm²^[28]。为了得到总面密度(包括热斑面密度和壳层面密度)的定标律^[3]，我们用MULTI-IFE程序模拟了从最大内爆速度时刻开始到靶丸最后飞散的过程中，热斑和壳层各个物理量的演化。我们在如下范围内，随机生成500组初始参数：壳层的初始质量m_s=200~400 μg、密度ρ_s=10~30 g/cm³、温度T_s=1~31 eV、速度v_imp=200~400 km/s，热斑的半径r_h=50~300 μm、密度ρ_h=0.01~0.26 g/cm³、温度T_h=0.1~1.6 keV。统计MULTI-IFE的输出结果后，得到了中间变量和总面密度ρr之间的数据，中间变量有壳层的质量m_s，动能k_s=m_sv_imp²/2，烧蚀压p_a，飞行熵增因子α_if，热斑的体积V_h=4πr_h³/3，质量m_h=ρ_hV_h，压力p_h=Γ_Bρ_hT_h，其中Γ_B=7.66×10¹⁴ erg/(g·keV)是氘氚气体常数。拟合数据得到

$\rho r=\left(4.5927 \times 10^{-6}\right) m_{\mathrm{s}}^{0.476} k_{\mathrm{s}}^{0.619} p_{\mathrm{a}}^{0.0325} \alpha_{\mathrm{if}}^{-0.369} V_{\mathrm{h}}^{-0.603} m_{\mathrm{h}}^{-0.0975} p_{\mathrm{h}}^{-0.274}$

(11)

如图 2所示是拟合结果的准确性效果，横坐标是MULTI-IFE计算得到的总面密度，纵坐标是用拟合后的定标律给出的数值，可见点火面密度的定标律式(11)拟合的很好。再忽略式(11)中次方小的项，可以得到ρr=(8.2968×10^-5)m_s^0.476k_s^0.624α_if^-0.342V_h^-0.694p_a^-0.327，由于加速阶段的火箭模型无法确定最大内爆速度时刻热斑的参数，所以取V_h为500组随机V_h的平均值，最后得总面密度的定标律为

$\rho r=(0.087325) m_{\mathrm{s}}^{0.476} k_{\mathrm{s}}^{0.624} \alpha_{\mathrm{if}}^{-0.342} p_{\mathrm{a}}^{-0.327}=(0.056663)\left(M_0 \delta\right)^{1.100} v_{\mathrm{imp}}^{1.248} \alpha_{\mathrm{if}}^{-0.342} p_{\mathrm{a}}^{-0.327}$

(12)

图 2 500组随机初始参数拟合的定标面密度效果

Figure 2. The scaling MULTI-IFE data vs of areal density

下载: 全尺寸图片幻灯片

文献[3]从广义劳森判据推得了总面密度定标律，文献[25]从流体动力学相似律等价理论出发推导得到了壳层面密度和热斑面密度的定标律。

由总面密度，我们可知氘氚燃料被点燃的比例即燃烧损耗^{[2, 25]}

${\mathit{\Phi}}=\frac{\rho r}{\rho r+H_{\mathrm{B}}}$

(13)

其中H_B=6 g/cm²是燃烧参数，氘氚燃料反应后的能量产额

$Q=Q_{\mathrm{DT}} \frac{m_{\mathrm{s}}}{5 m_{\mathrm{p}}} {\mathit{\Phi}}=\left(3.37184 \times 10^{18} \mathrm{erg} / \mathrm{g}\right) m_{\mathrm{s}} {\mathit{\Phi}}$

(14)

其中Q_DT=17.6 MeV是一对氘氚原子发生核反应放出的能量，m_p是单位原子质量。最后，靶丸内爆的能量增益为

$G=\frac{Q}{2.746 F}$

(14)

其中，已将通过靶丸初始表面的辐射能F=4σT_r⁴πR₀²τ=4πσT_r⁴R₀³/(v₀-5lnδT_r^0.5)耦合为间接驱动给与的激光能量E_laser=2.746F，即激光转换效率是36.42%，这个效率参考了文献[5, 30]的理论与数据。

1.4 点火裕量判据

我们还需要判断靶丸内爆点火的裕量，即是否能顺利点火。由劳森判据^[2-4]，阻滞时刻壳层的压强p和约束时间τ_c乘积必须满足

$p \tau_{\mathrm{c}}=\left(\frac{4 {\rm{ \mathsf{ π} }}}{3}\right)^{-1 / 3}\left(\frac{\gamma-1}{2}\right)^{1.5} \gamma^{-0.25} A_{\mathrm{deg}}^{-0.85} m_{\mathrm{s}}^{1 / 3} v_{\mathrm{imp}}^{2.5} \alpha_{\mathrm{if}}^{-0.85} p_{\mathrm{a}}^{0.1}>C$

(16)

所以对于能顺利点火的靶丸，其壳层加速完成时的质量

$m_{\mathrm{s}}>m_{\mathrm{min}}=C^3\left(\frac{4 {\rm{ \mathsf{ π} }}}{3}\right)\left[\left(\frac{\gamma-1}{2}\right)^{-4.5} \gamma^{0.75} A_{\mathrm{deg}}^{2.55}\right] v_{\mathrm{imp}}^{-7.5} \alpha_{\mathrm{if}}^{2.55} p_{\mathrm{a}}^{-0.3}$

(17)

故最小点火能量

$E_{\mathrm{igt}}=\frac{C^3}{2}\left(\frac{4 {\rm{ \mathsf{ π} }}}{3}\right)\left[\left(\frac{\gamma-1}{2}\right)^{-4.5} \gamma^{0.75} A_{\mathrm{deg}}^{2.55}\right] v_{\mathrm{imp}}^{-5.5} \alpha_{\mathrm{if}}^{2.55} p_{\mathrm{a}}^{-0.3}$

(18)

定义出一维点火阈值因子

$I T F_{1 \mathrm{D}}=\frac{\frac{1}{2} m_{\mathrm{s}} v_{\mathrm{imp}}^2}{E_{\mathrm{igt}}}=\left[C^{-3}\left(\frac{4 {\rm{ \mathsf{ π} }}}{3}\right)^{-1}\left(\frac{\gamma-1}{2}\right)^{4.5} \gamma^{-0.75} A_{\mathrm{deg}}^{-2.55}\right] m_{\mathrm{s}} \alpha_{\mathrm{if}}^{-2.55} v_{\mathrm{imp}}^{7.5} p_{\mathrm{a}}^{0.3}$

(19)

ITF_1D＞1的靶丸是可以点火的靶丸。再使用m_s=M₀δ，并且在一个典型的点火点(m_s=0.3 mg; v_imp=360 km/s; α_if=1.4; p_a=131.6 Mbar; ITF_1D=3.0)上确定常系数后有

$I T F_{1 \mathrm{D}}=\left(2.9145 \times 10^{-57}\right) M_0 \delta v_{\mathrm{imp}}^{7.5} \alpha_{\mathrm{if}}^{-2.55} p_{\mathrm{a}}^{0.3}$

(20)

ITF_1D描述了靶丸能否顺利点火。文献[3]从广义劳森判据推得了点火阈值因子，文献[29]讨论了考虑热斑扰动和热斑纯度后的点火阈值因子。

2. 模型结果及设计规律

通过上述内爆动力学模型，我们获得了靶丸设计参量与性能参量之间的定标关系。关键的靶丸设计参量有：靶丸烧蚀体的材料系数a, b，靶丸的装量M₀与初始半径R₀及其关联的剩余质量份额δ与形状因子A_r0，靶丸所处环境参量即黑腔的辐射温度T_r，靶丸的内爆过程参量飞行熵增因子α_if与初始内爆速度v₀。关键的靶丸性能参量有：点火阈值因子ITF_1D，核反应能量增益G，通过靶丸初始表面的辐射能F，靶丸的不稳定性增长因子G_f和允许的最大初始扰动η。通过分析这些设计参量与性能参量之间的变化关系，我们研究了靶丸设计参数空间的变化规律。

2.1 靶丸的点火岛区域

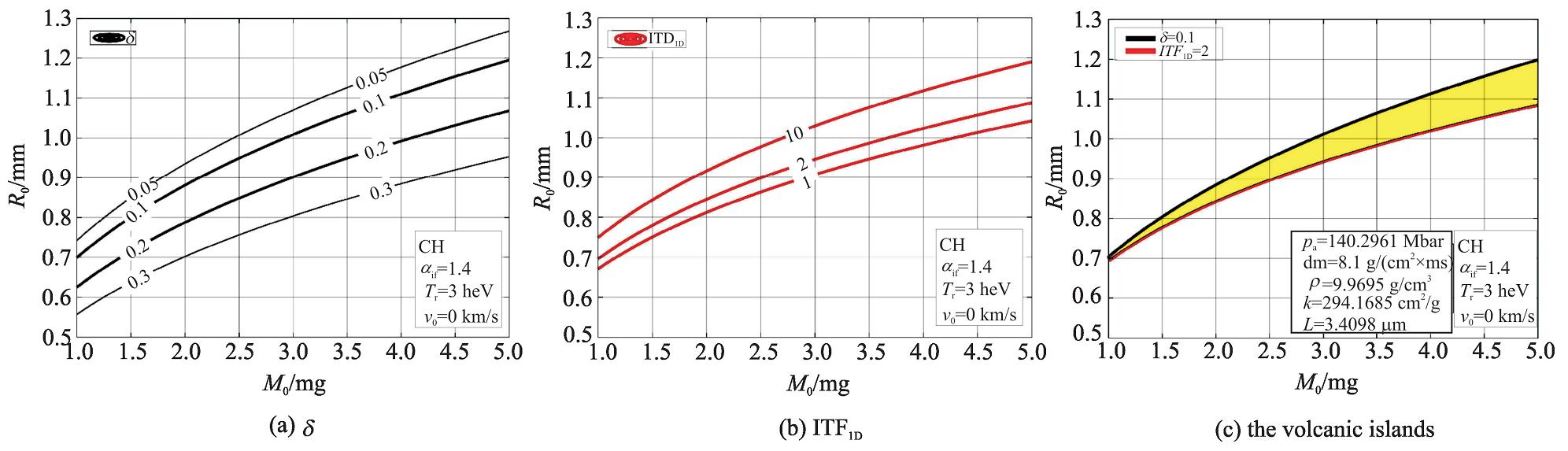
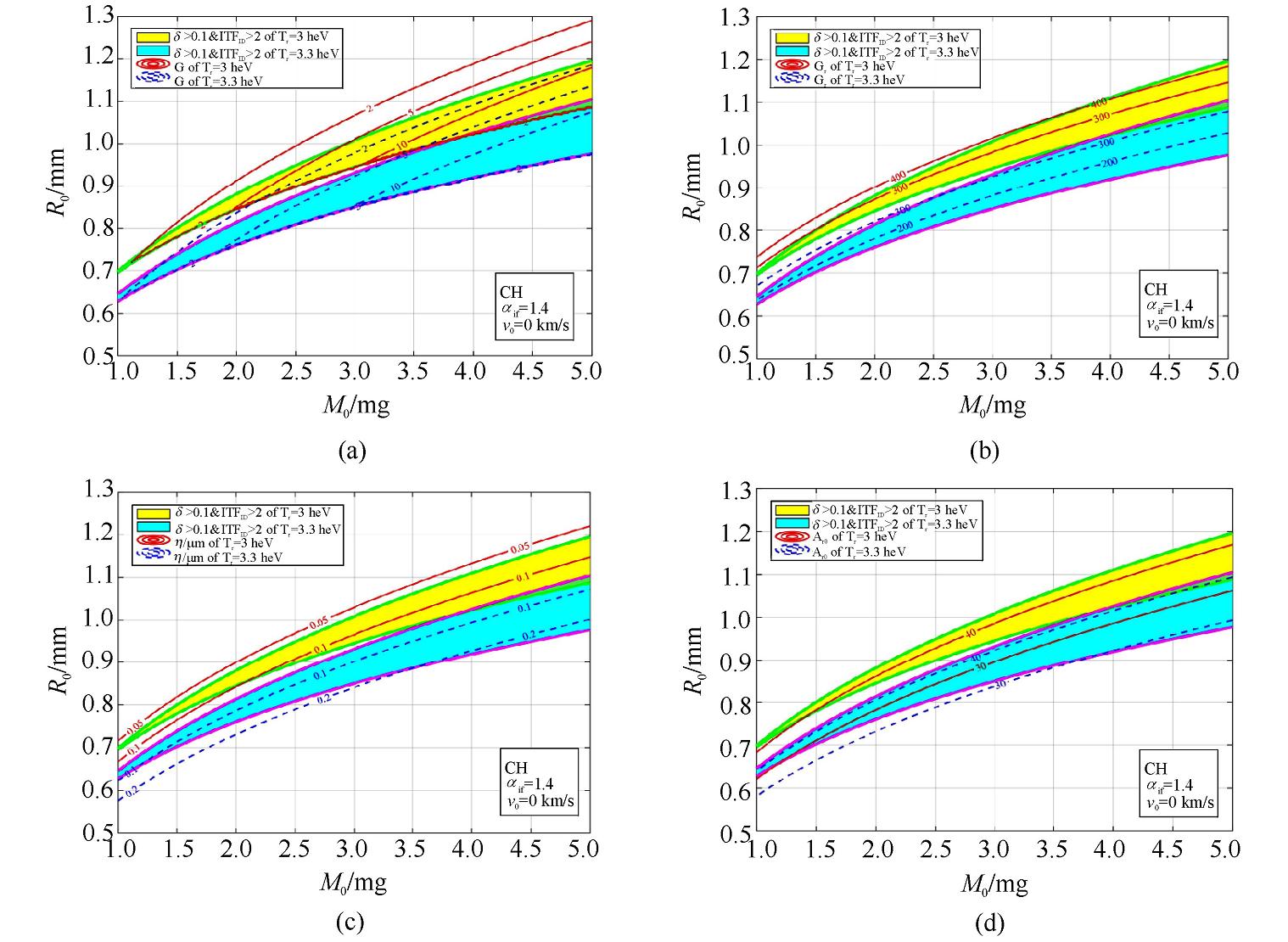
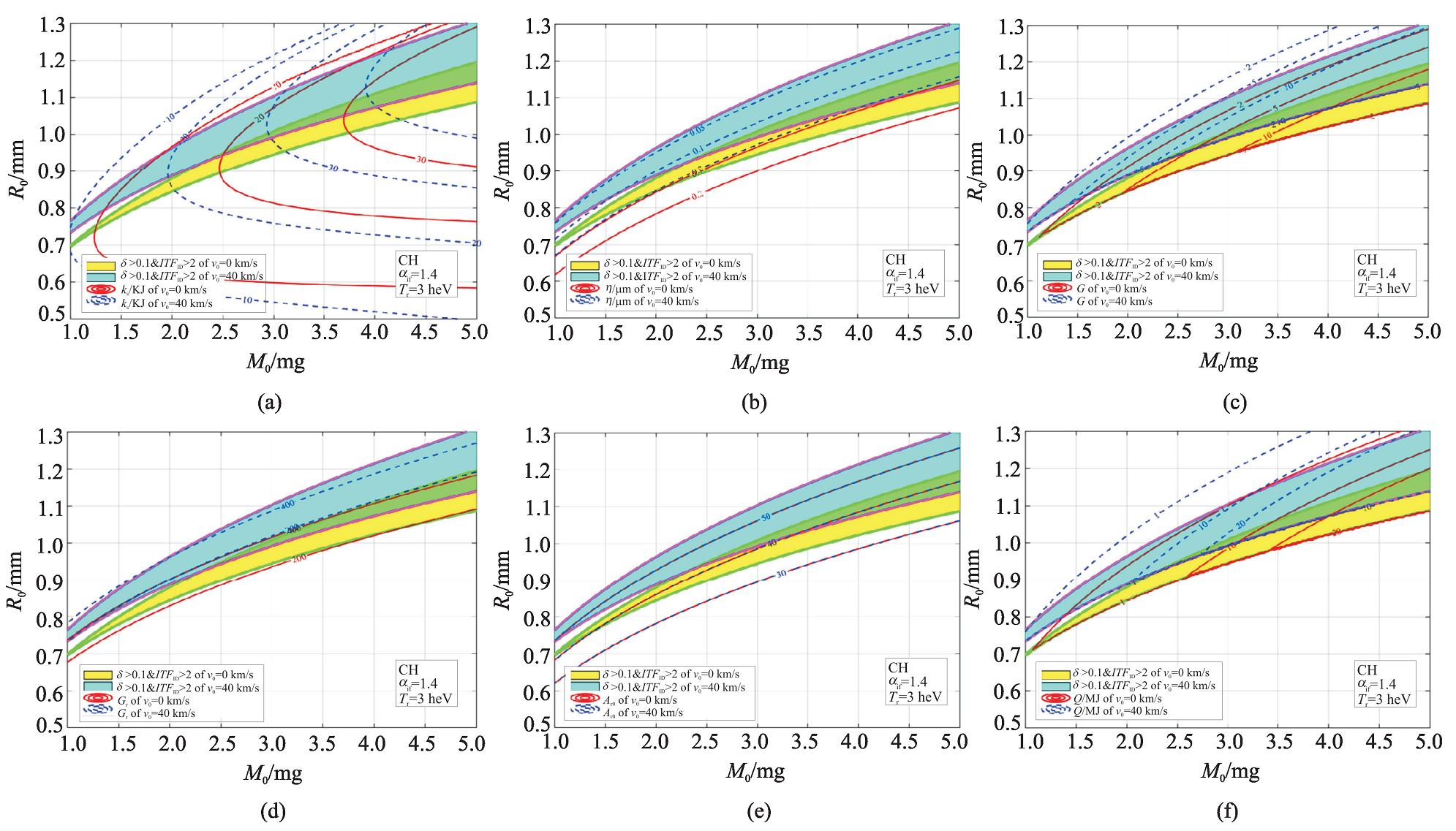
靶丸的性能参量随靶丸装量——半径的变化规律是基本的关注点。在确定的靶丸烧蚀材料CH，飞行熵增因子α_if=1.4，辐射温度T_r=3 heV和初始内爆速度v₀=0 km/s的条件下，我们获得图 3。由图 3(a)，对于确定的靶丸装量，靶丸的初始半径越大，被烧蚀的外表面越大，壳层加速完成时剩余质量份额越小。为了保留足够的燃料质量，需要δ＞0.1。由图 3(b)，点火阈值因子ITF_1D＞1才能顺利点火，考虑一定裕量，取ITF_1D＞2。δ＞0.1且ITF_1D＞2的区域即为靶丸点火所考虑的范围，如图 3(c)以黄色所示，即点火岛区域。

图 3 剩余质量比δ和点火阈值因子ITF_1D在靶丸装量——半径参数空间中的变化及点火岛区域

Figure 3. The contour of residual mass fraction δ and ignition threshold factor ITF_1D in the capsule mass-radius parameter space and the volcanic islands

下载: 全尺寸图片幻灯片

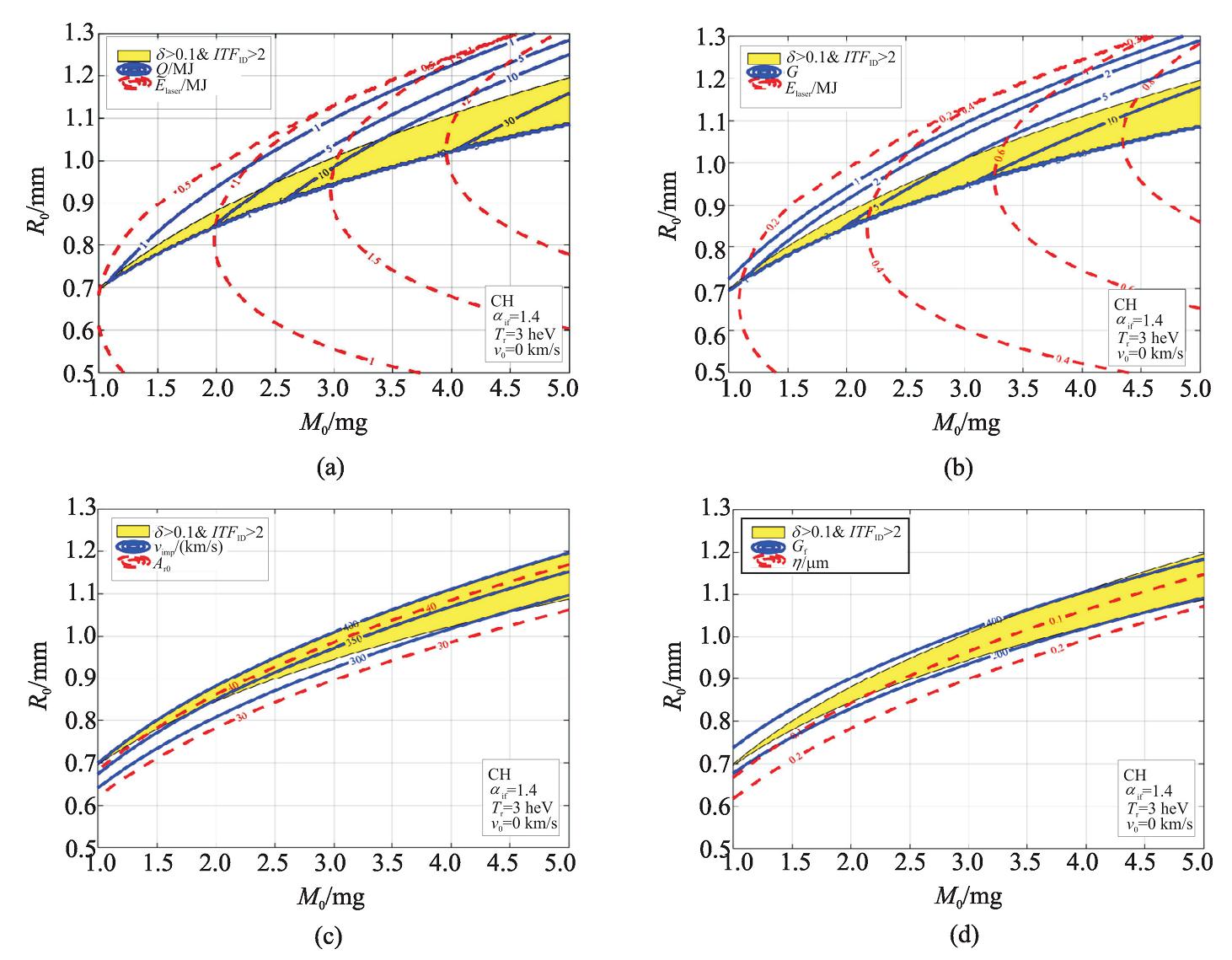
考虑点火岛中的性能参量。如图 4所示，初始装量为3 mg，初始半径为1 mm是主要参考点。该点靶丸需要消耗1.49 MJ激光能量转换为0.542 MJ通过靶丸初始表面的X射线能量，预计会产生8.46 MJ的聚变能得到5.69倍的能量增益。并且该靶丸在获得386.5 km/s的最大内爆速度时，壳层剩余质量份额为10.7%。靶丸的点火阈值因子ITF_1D=5.59，形状因子是41.76。加速阶段产生的烧蚀瑞利—泰勒不稳定性增长因子为346.3，故最大初始扰动不能超过0.07 μm。

图 4 点火岛中的参量

Figure 4. The parameters in the volcanic islands

下载: 全尺寸图片幻灯片

2.2 辐射温度对点火区域的影响

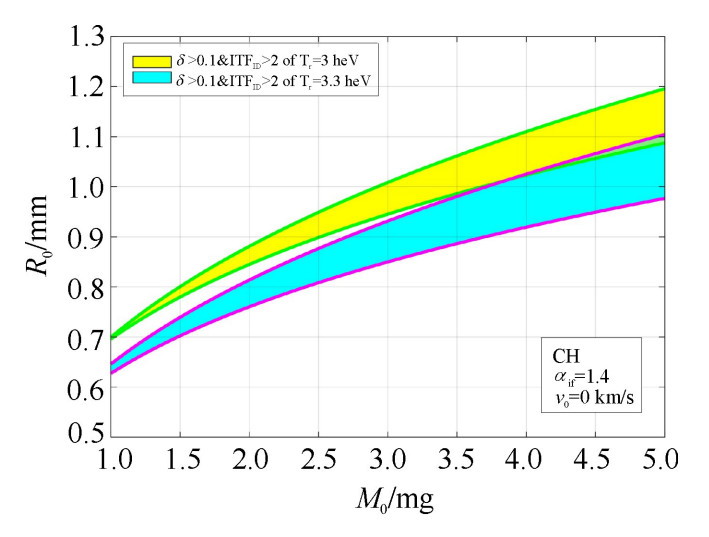
辐射温度T_r由3 heV增大到3.3 heV，质量烧蚀速率和烧蚀压增大，对装量相同的靶丸，为了保证烧蚀效果不变，必须减小靶丸受到烧蚀的面积，使得壳层所有的质量不被辐射烧蚀掉。如图 5所示，点火岛位置将向靶丸初始半径减小的方向移动，点火岛区域大小变化不显著。

图 5 辐射温度对点火岛的影响

Figure 5. The effect of radiation temperature on the volcanic islands

下载: 全尺寸图片幻灯片

如图 6所示，增大辐射温度后，虽然质量烧蚀速率和烧蚀压增大，但是在相同剩余质量份额的条件下，加速时间减小，使得通过靶丸初始表面的辐射能基本不变，需要的激光能量不变。靶丸产生的聚变能量与辐射温度无关，致使提高辐射温度后能量增益不变。增大辐射温度后，不稳定性的烧蚀致稳作用增强，不稳定性增长率和发展时间都变小，靶丸的稳定性变好，可以容忍更大的初始扰动。设计上，在靶丸装量不变的条件下，需要减小靶丸的半径，同时保证形状因子不变，所以靶丸的厚度也相应需要减小。

图 6 不同辐射温度下性能参量的比较

Figure 6. The comparisons of parameters in different radiation temperatures

下载: 全尺寸图片幻灯片

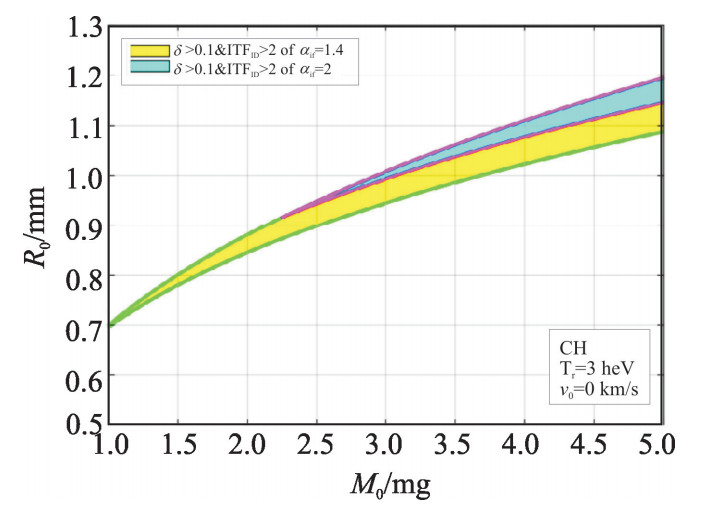
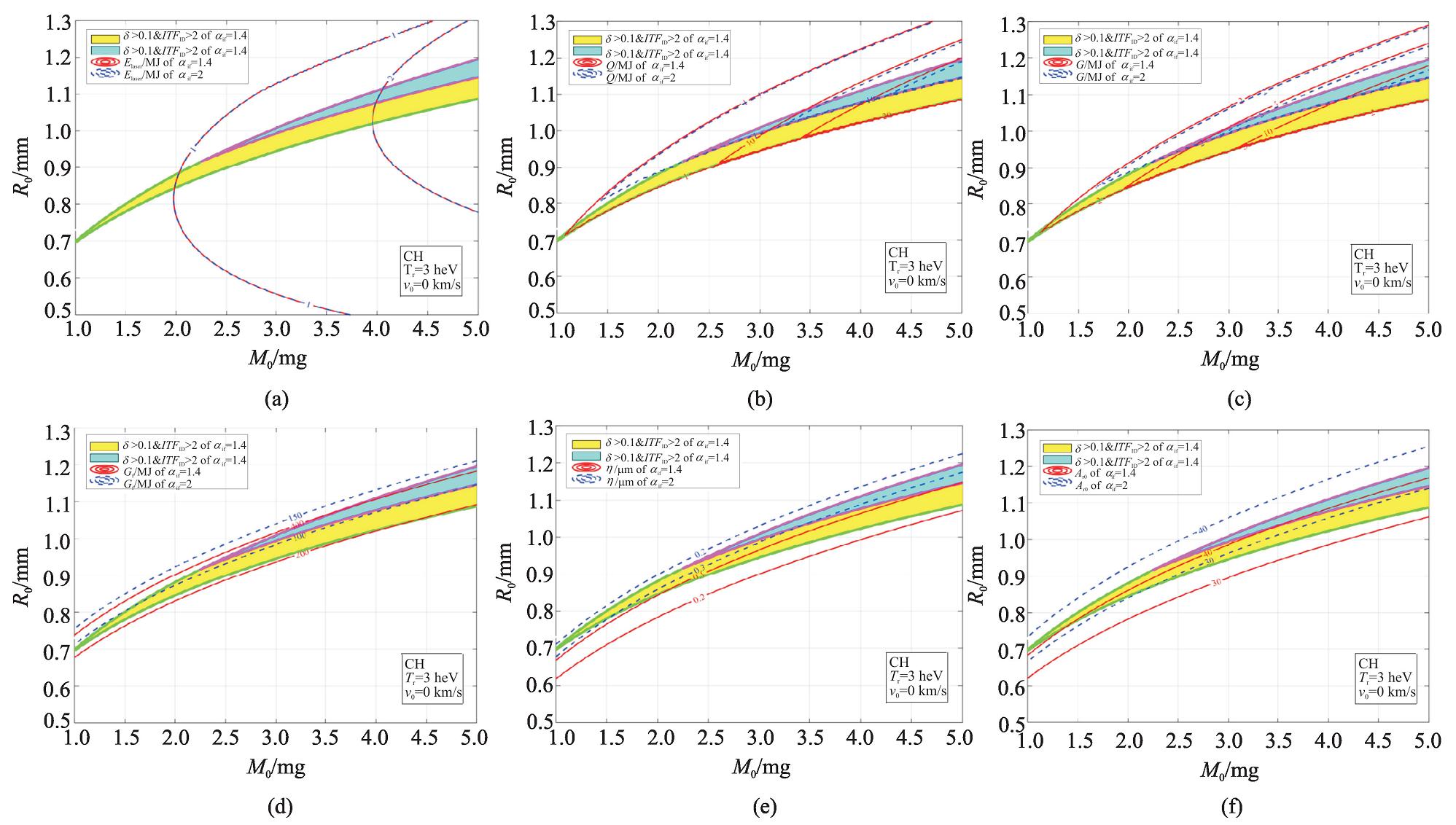
2.3 飞行熵增因子对点火区域的影响

飞行熵增因子α_if由1.4增大到2.0，虽然不影响壳层的最大内爆动能，但是阻滞时刻可以获得的压力变小密度变小，最小点火能量的增大使得点火阈值因子变小，最终导致点火岛变窄。如图 7所示，点火岛的位置不变，但是范围变小。

图 7 飞行熵增对点火区域的影响

Figure 7. The effect of in-flight adiabat on the volcanic islands

下载: 全尺寸图片幻灯片

如图 8所示，增大飞行熵增因子后，虽然通过靶丸初始表面的辐射能不变，需要的激光能量不变，但是点火面密度略微减小，产能因此减小，所以能量增益略微减小。增大飞行熵增因子后，加速阶段烧蚀体被压缩的密度减小，其平均光厚减小，密度梯度标长增大，烧蚀速度增加，故此烧蚀致稳作用增强。不稳定性增长因子变小，允许的最大初始扰动变大，内爆稳定性变好。另外，由于减小了壳层的压缩密度，设计上需要增加靶丸的初始厚度，形状因子因此变小。

图 8 不同飞行熵增下性能参量的比较

Figure 8. The comparisons of parameters in different in-flight adiabat

下载: 全尺寸图片幻灯片

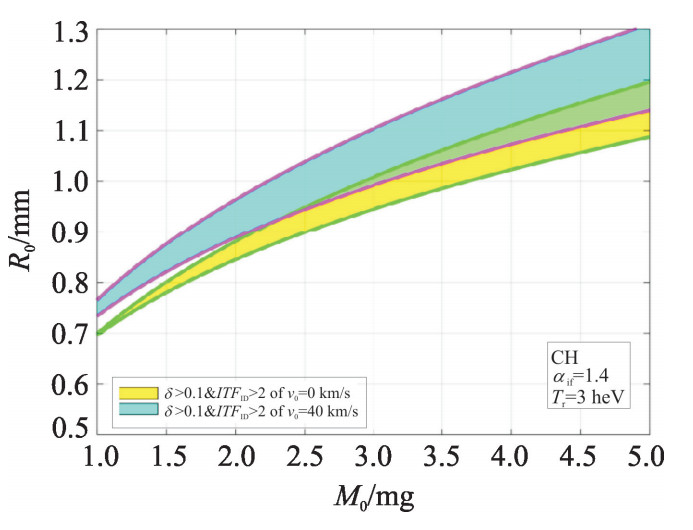
2.4 整形速度对点火区域的影响

整形速度v₀由0 km/s增大到40 km/s，根据式(2)在靶丸装量不变的条件下，相同剩余质量份额对应的靶丸初始半径增大，又由于整形速度对最大内爆速度的贡献，点火阈值因子提高。如图 9所示，点火岛的位置向靶丸初始半径增大的方向移动，点火岛的区域范围变大。

图 9 整形速度对点火区域的影响

Figure 9. The effect of shaping velocity on the volcanic islands

下载: 全尺寸图片幻灯片

如所示，增大初始整形速度后，虽然最大内爆速度增大，导致最大内爆动能增大。但是装量相同的靶丸初始半径增大，导致通过靶丸初始表面的辐射能增大，需要的激光能量增大。虽然内爆速度的增大对点火面密度有贡献，致使产能提高，但是权衡也增大的激光能量后，能量增益基本不变。增大初始整形速度后，内爆不稳定性增长因子的增加不超过 $\sqrt{v_{{\rm{i m p}}} /\left(v_{{\rm{i m p}}}-v_0\right)}$ 倍，对v_imp=300~400 km/s, v₀=40 km/s，不稳定性增长因子增加不会超过5.4%~7.4%，即内爆稳定性变化不显著。另外，由于相同装量下靶丸初始半径增大，设计上壳层初始厚度变小、形状因子变大。壳层厚度的变小使得允许的最大初始扰动变小。

图 10 不同整形速度下性能参量的比较

Figure 10. The comparisons of parameters in different shaping velocity

下载: 全尺寸图片幻灯片

2.5 靶丸烧蚀材料对点火区域的影响

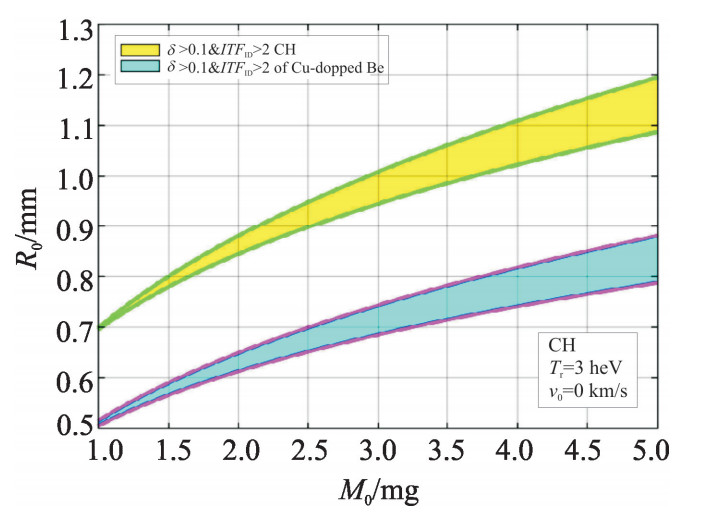
当改变靶丸的烧蚀材料，提高质量烧蚀速率与烧蚀压时，根据式(2)对于相同的δ参数D₀是不变的，质量烧蚀速率 $\dot m$ 的提高使得R₀减小，有R₀~a^-1/3或b~R₀^-3。点火阈值因子不受影响，只是跟着δ移动位置。如图 11所示，点火岛向靶丸初始半径减小的方向移动，点火岛的区域范围大小不变。

图 11 靶丸烧蚀材料对点火区域的影响

Figure 11. The effect of ablator material on the volcanic islands

下载: 全尺寸图片幻灯片

如图 12所示，当改变靶丸的烧蚀材料，提高质量烧蚀速率与烧蚀压时，由于初始半径R₀明显减小, 通过靶丸初始表面的辐射能明显减小，需要的激光能量明显减小。点火面密度不受影响产能不变，由于节约了驱动能量，所以能量增益变大。另外，虽然烧蚀材料烧蚀性能的改变，增大了烧蚀体的密度ρ~b^0.6，使得烧蚀体的平均光厚增大κ_p~b^0.6，密度梯度标长减小L~b^-1.2，但是初始半径减小的效应更强。最终效果是增大了烧蚀速度v_a~b^-0.6R₀^-4~b^0.73，增加了烧蚀致稳~b^1.06的效果，不稳定性增长因子明显减小，可以容忍的初始扰动增大，稳定性明显变好。设计上，对于装量相同的靶丸由于初始半径的减小，初始厚度需要增加，靶丸形状因子减小。

图 12 不同靶丸烧蚀材料下性能参量的比较

Figure 12. The comparisons of parameters in different ablator material

下载: 全尺寸图片幻灯片

3. 结论

本文通过理论方法和一维流体力学模拟，给出了激光间接驱动点火靶丸内爆过程的定标律公式。通过这些定标律公式获得了在给定黑腔辐射温度、飞行熵增因子、整形速度和烧蚀材料的条件下，靶丸装量——半径参数空间的点火岛区域。研究了靶丸性能参数随辐射温度、飞行熵增因子等的变化规律：(1)当靶丸所处黑腔辐射温度升高时，内爆的稳定性将变好；设计上在靶丸装量不变的条件下，靶丸半径需要减小。(2)当靶丸的飞行熵增因子增大时，内爆增益略微减小，内爆稳定性变好；但是点火阈值因子减小导致点火岛的区域变窄。(3)当靶丸的整形速度增大时，点火岛的区域略微变大，内爆稳定性变化不显著；设计上在靶丸装量不变的条件下，需要增大靶丸半径，这会导致靶丸壳层形状因子变大。(4)当改变靶丸烧蚀材料，提高质量烧蚀速率与烧蚀压时，能量增益变大且稳定性增强；设计上在靶丸装量不变的条件下，需要减小靶丸半径。

通过这些分析，我们获得了改进靶丸性能的几种方案：增大辐射温度、增大飞行熵增因子可增强A-RT不稳定性的烧蚀致稳作用，减弱内爆不稳定性；增大整形速度，可提高产能，但是并不能有效提高增益；改变靶丸的烧蚀材料提高质量烧蚀速率与烧蚀压，可以节约激光能量提高能量增益并控制不稳定性。在后续工作中，我们将进一步精细化分析影响靶丸增益和内爆不稳定性的物理机制，寻找更佳的优化设计方案。

图 1 发射器及冷却管道基本结构

Figure 1. Basic structure of EML launcher and cooling pipes

下载: 全尺寸图片幻灯片

图 2 预紧状态下的轨道应力分布

Figure 2. Preload von Mises stress in rail

下载: 全尺寸图片幻灯片

图 3 轨道横截面2D电磁场计算

Figure 3. Electromagnetic field calculation

下载: 全尺寸图片幻灯片

图 4 轨道横截面电磁力分布

Figure 4. Electromagnetic force distribution in rails cross section

下载: 全尺寸图片幻灯片

图 5 预紧力和电磁力共同作用下的轨道横截面应力分布

Figure 5. Von Mises stress in the rail under preload and electromagnetic force

下载: 全尺寸图片幻灯片

图 6 管道位于不同位置时的轨道形变

Figure 6. Displacement of rail with pipe

下载: 全尺寸图片幻灯片

图 7 轨道横截面电流密度

Figure 7. Rail current density

下载: 全尺寸图片幻灯片

图 8 管道位于不同位置时的轨道电感梯度

Figure 8. Inductance gradient of rail with pipe

下载: 全尺寸图片幻灯片

表 1 各材料力学性能参数

Table 1. Mechanical properties parameters of materials

	ρ/(kg·m^-3)	Young’s modulus/Pa	Poisson’s ratio
rail	8890	1.10×10¹¹	0.35
bolt	7850	2.06×10¹¹	0.30
insulation	1420	1.40×10¹⁰	0.33
steel bar	8000	1.93×10¹¹	0.29

下载: 导出CSV

表 2 仿真模型中轨道材料属性

Table 2. Rail material properties of simulation model

material	μ_r	σ/(S·m^-1)	ρ/(kg·m^-3)
C18200	1	4.63×10⁷	8890

下载: 导出CSV

参考文献(18)

[1]	Marshall R A, Ying W. Railguns: Their science and technology[M]. Beijing: China Machine Press, 2004: 32-35.
[2]	Fair H D. The past, present, and future of electromagnetic launch technology and IEEE International EML Symposium[J]. IEEE Trans Magnetics, 2013, 41(1): 1024-1027.
[3]	李军, 严萍, 袁伟群. 电磁轨道炮发射技术的发展与现状[J]. 高电压技术, 2014, 40(4): 1052-1064. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201404015.htm Li Jun, Yan Ping, Yuan Weiqun. Electromagnetic gun technology and its development. High Voltage Engineering, 2014, 40(4): 1052-1064 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201404015.htm
[4]	Motes D, Keena J, Womack K, et al. Thermal analysis of high-energy railgun tests[J]. IEEE Trans Plasma Science, 2012, 40(1): 124-30.
[5]	Myers S H, Smith A N. Demonstration of combined spray and evaporative cooling of an electromagnetic railgun[J]. IEEE Trans Magnetics, 2009, 45(1): 396-401.
[6]	Jamison K A, Petresky H L, Beavers F L, et al. Thermal loading and heat removal from a sequentially fired railgun[J]. IEEE Trans Magnetics, 1995, 31(1): 314-319. doi: 10.1109/20.364669
[7]	Fish S, Phipps C, Tang V. Rail heating analysis for multishot EM gun operation[J]. IEEE Trans Magnetics, 1999, 35(1): 398-402. doi: 10.1109/20.738439
[8]	Kealey E R. Investigation of elliptical cooling channels for a naval electromagnetic railgun[C]//ASME 2005 International Mechanical Engineering Congress and Exposition. 2005: 89-97.
[9]	Lin L, Yuan W, Zhao Y, et al. Thermal analysis on electromagnetic launcher under transient conditions[J]. IEEE Trans Plasma Science, 2017, 45(7): 1476-1481. doi: 10.1109/TPS.2017.2705725
[10]	Zhao H, Souza J A, Ordonez J C. Thermal model for electromagnetic launchers[J]. Therm Eng, 2008, 7(2): 59-64.
[11]	Zhao H, Souza J A, Ordonez J C. Three-dimensional launch simulation and active cooling analysis of a single-shot electromagnetic railgun[J]. Simulation: Transactions of the Society for Modeling and Simulation International, 2014, 90(12): 1312-1327. doi: 10.1177/0037549714553812
[12]	许镇宇, 朱景梓, 郑林庆, 等. 机械零件[M]. 北京: 人民教育出版社, 1960. Xu Zhenyu, Zhu Jingzi, Zheng Linqing, et al. Mechanical parts. Beijing: People's Education Press, 1960
[13]	王朋, 陈安生, 张会武, 等. 螺栓扭矩系数影响因素的试验研究[J]. 实验力学, 2013, 28(3): 307-313. https://www.cnki.com.cn/Article/CJFDTOTAL-SYLX201303006.htm Wang Peng, Chen Ansheng, Zhang Huiwu, et al. Experimental study of the factors effecting on bolt torque coefficient. Journal of Experimental Machanics, 2013, 28(3): 307-313 https://www.cnki.com.cn/Article/CJFDTOTAL-SYLX201303006.htm
[14]	赵莹, 徐蓉, 袁伟群, 等. 脉冲大电流电磁轨道发射装置特性[J]. 强激光与粒子束, 2014, 26: 095004. doi: 10.11884/HPLPB201426.095004 Zhao Ying, Xu Rong, Yuan Weiqun, et al. Charateristics of high pulsed current electromagnetic rail launcher. High Power Laser and Particle Beams, 2014, 26: 095004 doi: 10.11884/HPLPB201426.095004
[15]	林灵淑, 赵莹, 袁伟群, 等. 电磁轨道发射的瞬态温度效应[J]. 高电压技术, 2016, 42(9): 2864-2869. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201609023.htm Lin Lingshu, Zhao Ying, Yuan Weiqun, et al. Thermal analysis of railgun tests under transient conditions. High Voltage Engineering, 2016, 42(9): 2864-2869 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201609023.htm
[16]	杨玉东, 王建新, 薛文. 轨道炮速度趋肤效应的分析与仿真[J]. 强激光与粒子束, 2011, 23(7): 1965-1968. http://www.hplpb.com.cn/article/id/5320 Yang Yudong, Wang Jianxin, Xue Wen. Simulation and analysis of velocity skin effect of railgun. High Power Laser and Particle Beams, 2011, 23(7): 1965-1968 http://www.hplpb.com.cn/article/id/5320
[17]	Marshall R A, 王莹. 电磁轨道炮的科学与技术[M]. 北京: 兵器工业出版社, 2006.
[24]	Marshall R A, Wang Ying. Railguns: their science and technology. Beijing: The Publishing House of Ordnance Industry, 2006

施引文献

资源附件(0)

访问统计

点击查看大图

图(8) / 表(2)

计量

文章访问数: 1165
HTML全文浏览量: 329
PDF下载量: 175
被引次数: 0

1. 理论模型
1.1 加速阶段
1.2 减速阶段
1.3 聚变点火与燃烧
1.4 点火裕量判据
2. 模型结果及设计规律
2.1 靶丸的点火岛区域
2.2 辐射温度对点火区域的影响
2.3 飞行熵增因子对点火区域的影响
2.4 整形速度对点火区域的影响
2.5 靶丸烧蚀材料对点火区域的影响
3. 结论

1. 理论模型
1.1 加速阶段
1.2 减速阶段
1.3 聚变点火与燃烧
1.4 点火裕量判据
2. 模型结果及设计规律
2.1 靶丸的点火岛区域
2.2 辐射温度对点火区域的影响
2.3 飞行熵增因子对点火区域的影响
2.4 整形速度对点火区域的影响
2.5 靶丸烧蚀材料对点火区域的影响
3. 结论

参考文献(18)

施引文献

资源附件(0)

访问统计

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

电磁发射装置轨道热管理冷却管道的力学设计

doi: 10.11884/HPLPB201830.170322

作者简介:
林灵淑(1991—)，女，博士研究生，主要从事脉冲功率技术的研究；linlingshu13@mail.iee.ac.cn

通讯作者:
严萍(1966—)，女，博士，研究员，主要从事高电压绝缘技术和脉冲大电流放电技术的研究；pingyan@mail.iee.ac.cn

计量

Mechanical design of rail cooling pipe for electromagnetic launcher

1. 理论模型

1.1 加速阶段

1.2 减速阶段

1.3 聚变点火与燃烧

1.4 点火裕量判据

2. 模型结果及设计规律

2.1 靶丸的点火岛区域

2.2 辐射温度对点火区域的影响

2.3 飞行熵增因子对点火区域的影响

2.4 整形速度对点火区域的影响

2.5 靶丸烧蚀材料对点火区域的影响

3. 结论

计量

目录

1. 理论模型

1.1 加速阶段

1.2 减速阶段

1.3 聚变点火与燃烧

1.4 点火裕量判据

2. 模型结果及设计规律

2.1 靶丸的点火岛区域

2.2 辐射温度对点火区域的影响

2.3 飞行熵增因子对点火区域的影响

2.4 整形速度对点火区域的影响

2.5 靶丸烧蚀材料对点火区域的影响

3. 结论

留言板

电磁发射装置轨道热管理冷却管道的力学设计

doi: 10.11884/HPLPB201830.170322

作者简介: 林灵淑(1991—)，女，博士研究生，主要从事脉冲功率技术的研究；linlingshu13@mail.iee.ac.cn

通讯作者: 严萍(1966—)，女，博士，研究员，主要从事高电压绝缘技术和脉冲大电流放电技术的研究；pingyan@mail.iee.ac.cn

计量

出版历程

Mechanical design of rail cooling pipe for electromagnetic launcher

1. 理论模型

1.1 加速阶段

1.2 减速阶段

1.3 聚变点火与燃烧

1.4 点火裕量判据

2. 模型结果及设计规律

2.1 靶丸的点火岛区域

2.2 辐射温度对点火区域的影响

2.3 飞行熵增因子对点火区域的影响

2.4 整形速度对点火区域的影响

2.5 靶丸烧蚀材料对点火区域的影响

3. 结论

计量

出版历程

目录

1. 理论模型

1.1 加速阶段

1.2 减速阶段

1.3 聚变点火与燃烧

1.4 点火裕量判据

2. 模型结果及设计规律

2.1 靶丸的点火岛区域

2.2 辐射温度对点火区域的影响

2.3 飞行熵增因子对点火区域的影响

2.4 整形速度对点火区域的影响

2.5 靶丸烧蚀材料对点火区域的影响

3. 结论

作者简介:
林灵淑(1991—)，女，博士研究生，主要从事脉冲功率技术的研究；linlingshu13@mail.iee.ac.cn

通讯作者:
严萍(1966—)，女，博士，研究员，主要从事高电压绝缘技术和脉冲大电流放电技术的研究；pingyan@mail.iee.ac.cn