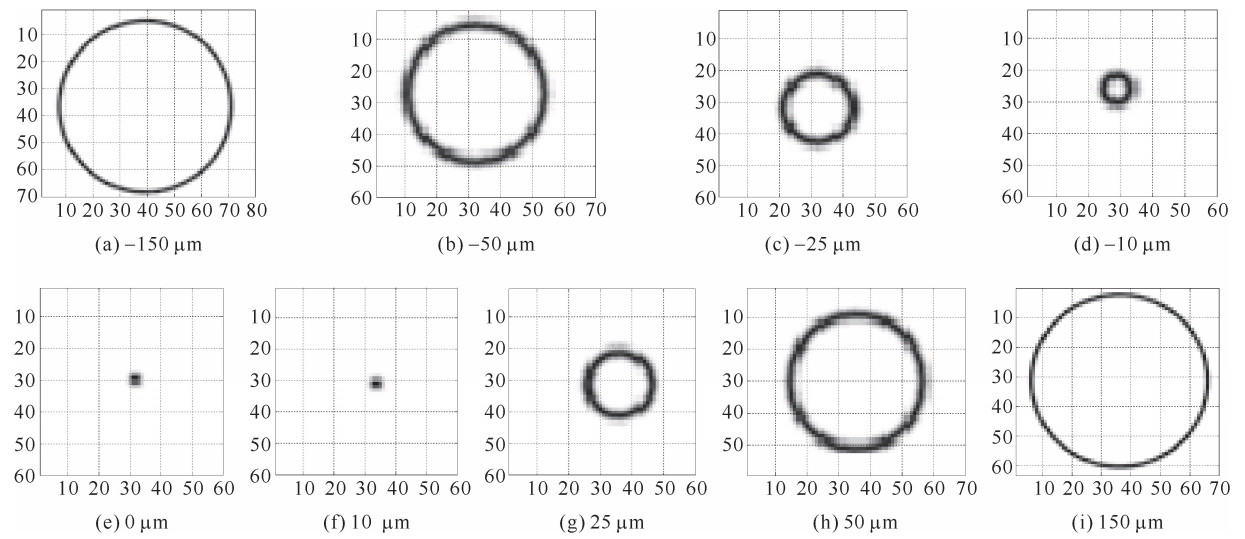
Simulation of Wolter microscope imaging system by ray-tracing
-
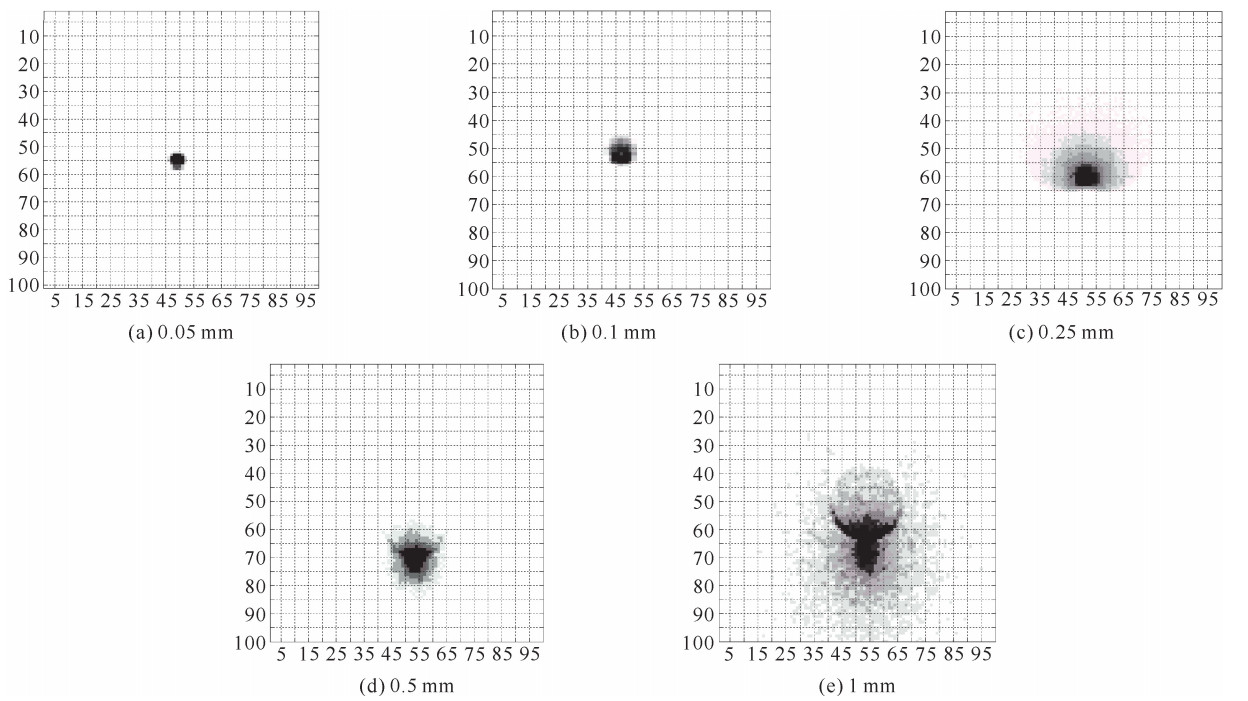
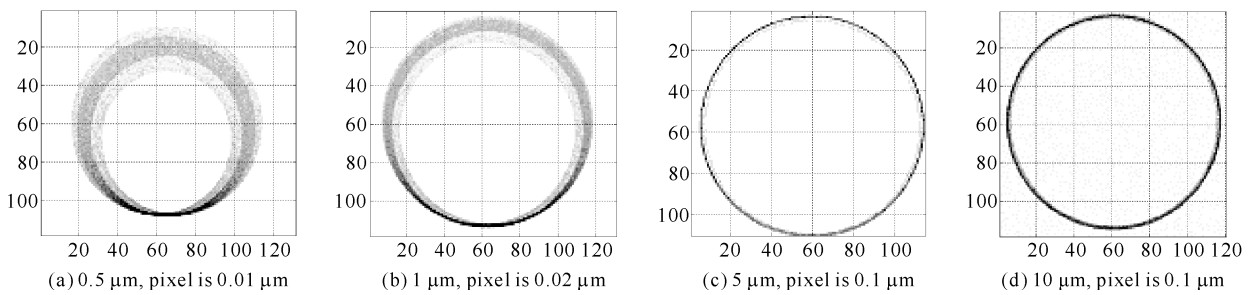
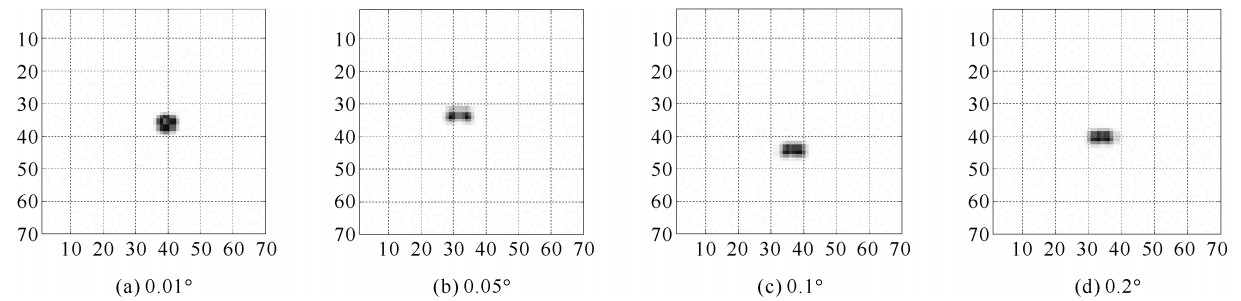
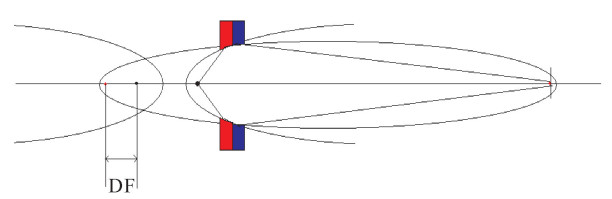
摘要: 利用光学设计软件ZEMAX模拟Wolter显微镜对点光源成像。在只考虑几何光学成像的条件下，分三种情况讨论：两曲面同轴共焦点，两曲面不同轴，两曲面同轴不共焦点，对点源通过Wolter系统成像分别进行了光线追踪模拟。通过模拟，定量给出了Wolter显微镜的焦深和景深，分析了处于不同视场点源所成的像，以及两个曲面不同轴时和不共焦点的情况下点源所成的像, 得知Wolter显微镜对物像距的要求很严格，两曲面的不同轴度和两曲面的不共焦点对成像影响非常大，这些模拟结果为Wolter显微镜的成像分析提供了依据。Abstract: The optical design software ZEMAX is used to simulate the imaging of a point source for Wolter microscope. Considering the imaging of geometrical optics only, three instances are considered, including the two surfaces coaxial and cofocal, non-coaxial, and coaxial but not confocal. The imaging of a point source is discussed respectively. The depth of focus and the depth of field are given. The imaging of a point source in different fields is also analyzed. It is concluded that Wolter microscope is very strict with the object distance and image distance. The influence of the two surfaces' non-coaxiality and non-confocality is much great on imaging. These results provides basis for imaging analysis of Wolter microscope.
-
Key words:
- Wolter microscope /
- ZEMAX simulation /
- ray-tracing /
- field
-
图 2 像面偏离像点后点光源所成的像(像素为1 μm)
Figure 2. Images of a point source on the imaging plane at a distance from the image point
图 3 点光源偏离物点后所成的像(像素为1 μm)
Figure 3. Images of a point source at a distance from the object point
图 5 Wolter显微镜的两曲面不同轴的两种情况
Figure 5. Instances of two non-coaxial surfaces of Wolter microscope
图 6 两曲面不同轴(两个轴平行) 时点光源所成的像
Figure 6. Images of a point source while the Wolter mirror has two parallel but non-coaxial surfaces with different vertical shift of one surface from the other
图 7 两曲面不同轴(两个轴不平行) 时点光源所成的像(像素为0.2 μm)
Figure 7. Images of a point source while the axes of the two surfaces are at different angles
图 8 Wolter显微镜的两曲面不共焦点示意图
Figure 8. Schematic of the two coaxial but nonfocal surfaces, DF represents the distance between the left focus of the hyperboloid and that of the euipsoid
-
[1] Wolter H. Generalized Schwarzs Childsche systems as reflection optics[J]. Ann Phys, 1952, 10: 94. [2] Price R H. X ray microscopy using grazing incidence reflection optics[J]. AIP Conf Proc, 1981, 75: 189. doi: 10.1063/1.33166 [3] Lindl J. Development of the indirect-drive approach to inertial confinement fusion and the target physics for ignition and gain[J]. Phys Plasmas, 1995, 2(11) : 3933-4024. doi: 10.1063/1.871025 [4] 胡家升. 光学工程导论[M]. 大连: 大连理工大学出版社, 2002: 800-816.Hu Jiasheng. Introduction to optical engineering. Dalian: Dalian University of Technology Press, 2002: 800-816 [5] 缪文勇. R-T流体力学不稳定性与混合诊断技术[M]//中国工程物理研究院年报. 1998.Miao Wenyong. The hybrid diagnosis technology of the R-T hydrodynamics instability//Annual Report of China Academy of Engineering Physics. 1998 [6] Janes E H, Andrey K, Patrick L. Grazing-incidence hyperboloid-hyperboloid designs for wide-field X-ray imaging applications[J]. Appl Opt, 2001, 40(1) : 136. doi: 10.1364/AO.40.000136 期刊类型引用(1)
1. 黄智峰，徐波. 聚氨酯合成革材料的制备及其在运动鞋中的应用. 中国皮革. 2022(11): 108-112 . 
百度学术其他类型引用(0)
-
下载:
点击查看大图
计量
- 文章访问数: 1200
- HTML全文浏览量: 385
- PDF下载量: 134
- 被引次数: 1
