A time-domain method for the electromagnetic transient response of multiconductor transmission lines excited by the electromagnetic pulse
-
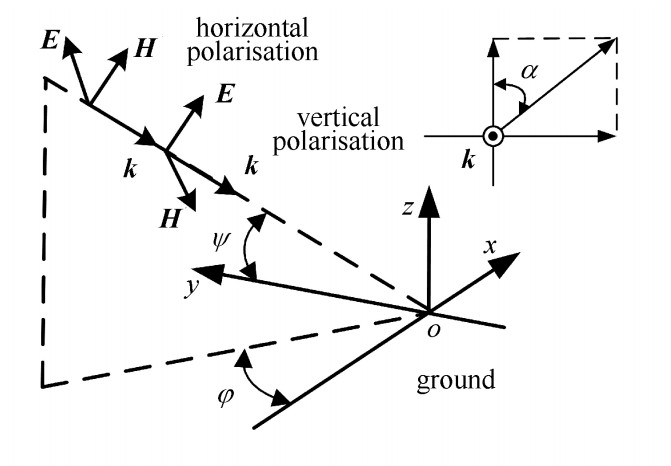
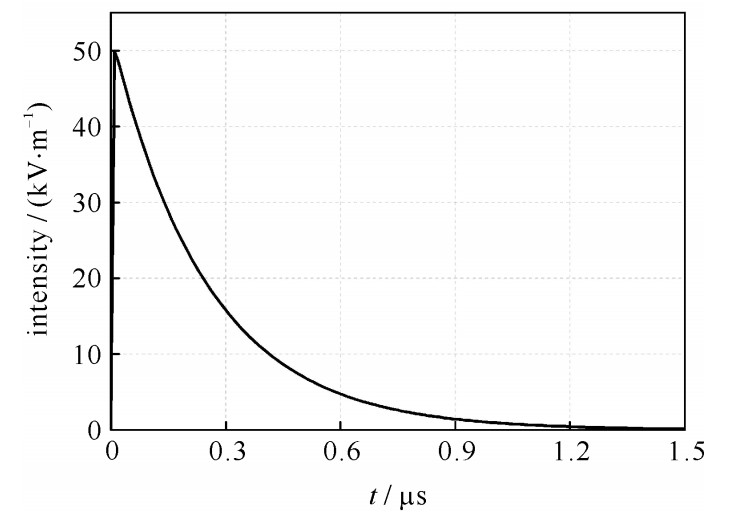
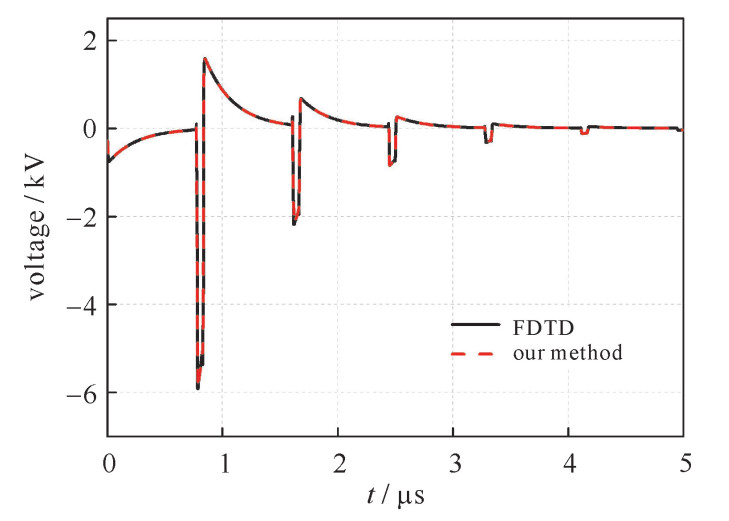
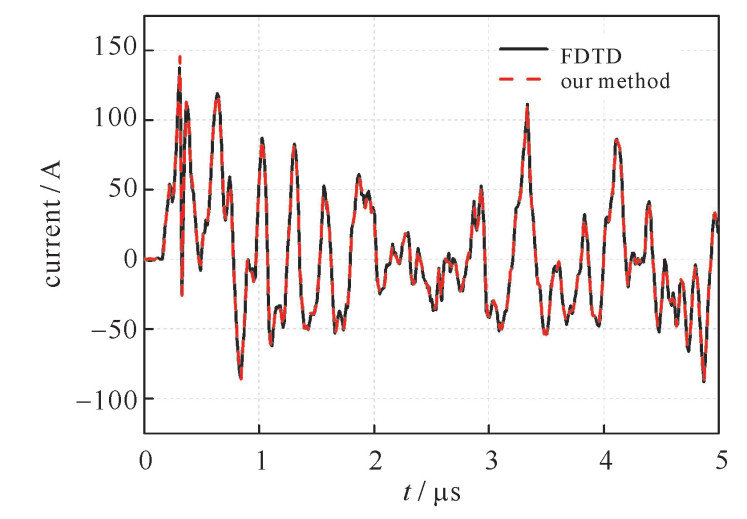
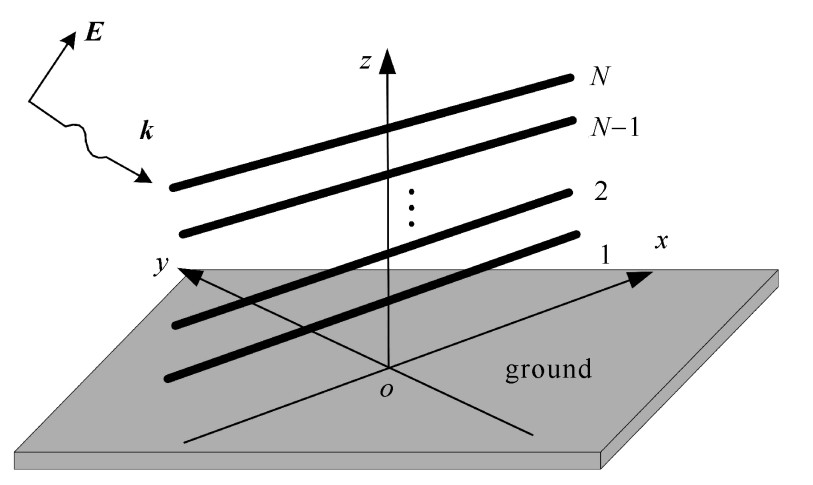
摘要: 基于波形松弛技术, 提出一种计算外界电磁脉冲激励下理想大地上无损多导体传输线瞬态响应的时域迭代方法。首先利用波形松弛技术对复频域内多导体传输线的电报方程进行解耦, 其中相邻导线的耦合作用等效为线上的分布源, 从而使电报方程转换为一系列关于独立导线的解耦方程组; 然后将复频域内传输线的解耦方程转换到时域, 根据时域方程建立相应的等效电路; 最后利用电路仿真软件PSCAD计算电磁脉冲激励下多导体传输线的瞬态响应。本文时域方法的计算结果与时域有限差分(FDTD) 法计算的结果进行对比, 证实了该时域方法的有效性和准确性, 这为工程和科研人员快速评估、分析电磁脉冲激励下多导体传输线的瞬态响应问题提供了一种可靠方法。Abstract: An efficient field-to-line coupling method in the time-domain is developed based on the waveform relaxation (WR) techniques for evaluating the electromagnetic (EM) transient response of multiconductor transmission lines (MTLs) excited by an electromagnetic pulse (EMP).Firstly, the incident EMP electric fields on the lines are calculated as equivalent distributed sources introduced into the MTLs equations.Then, the telegraph's equations of lossless transmission lines are decoupled by applying the WR techniques and different types of equivalent current sources at the terminal of MTLs are calculated using the iterative convolution and analytical method separately.Finally, the equivalent circuit is established and the transient currents/voltages induced on the lines are obtained by using the circuit simulation software PSCAD.The proposed time-domain method has the advantages of accuracy and high efficiency compared with the method based on finite-difference time-domain (FDTD) via two numerical examples.
-
图 1 外界电磁脉冲激励下的多导体传输线示意图
Figure 1. Geometry of the MTLs over the ground excited by the EMP
图 5 传输线1始端负载处感应电压计算结果对比图
Figure 5. Comparison of transient voltage induced at beginning of transmission line 1 obtained by FDTD and our method
图 6 传输线1终端负载处感应电压计算结果对比图
Figure 6. Comparison of transient voltage induced at the terminal of transmission line 1 obtained by FDTD and our method
图 7 传输线1终端负载处感应电压计算结果对比图
Figure 7. Comparison of transient voltage induced at the terminal of transmission line 1 obtained by FDTD and our method
图 8 传输线2终端负载处感应电流计算结果对比图
Figure 8. Comparison of transient current induced at the terminal of transmission line 2 obtained by FDTD and our method
表 1 传输线终端连接的集总参数网络类型
Table 1. The types of lumped networks at terminal of transmission lines
transmission line terminal load type value line1 RL1 parallel C1 50 Ω, 5 nF line2 RL2 series L2 50 Ω, 10 μH line3 RL3 series L3, C3 100 Ω, 0.2 μH, 10 nF 
下载: 导出CSV
-
[1] Savage E, Gilbert J, Radasky W. The early-time (E1) high-altitude electromagnetic pulse (HEMP) and its impact on the U. S. power grid[R]. Meta-R-320, 2010 [2] Sabath F, Potthast S. Tolerance values and the confidence level for high-altitude electromagnetic pulse (HEMP) field tests[J]. IEEE Trans Electromagnetic Compatibility, 2013, 55(3): 1529-1538. [3] Wraight A, Prather W D, Sabath F. Development in early-time (E1) high-altitude electromagnetic pulse (HEMP) test methods[J]. IEEE Trans Electromagnetic Compatibility, 2013, 55(3): 492-499. doi: 10.1109/TEMC.2013.2241442 [4] 谢彦召, 王赞基, 王群书. 地面附近架高线缆HEMP响应计算的Agrawal和Taylor模型比较[J]. 强激光与粒子束, 2005, 17(4): 575-580. (Xie Yanzhao, Wang Zanji, Wang Qunshu. Comparison of Agrawal and Taylor models for response calculation of above ground cable excited by HEMP. High Power Laser and Particle Beams, 2005, 17(4): 575-580) http://www.hplpb.com.cn/article/id/94 [5] 毛从光, 孙东阳, 孙蓓云. 架空线缆电磁脉冲响应的统计特性[J]. 强激光与粒子束, 2015, 27: 073203. (Mao Congguang, Sun Dongyang, Sun Beiyun. Statistical study on response of overhead line to electromagnetic pulse. High Power Laser and Particle Beams, 2015, 27: 073203) doi: 10.11884/HPLPB201527.073203 [6] Xie H Y, Du T J, Zhang M Y, et al. Theoretical and experimental study of effective coupling length for transmission lines illuminated by HEMP[J]. IEEE Trans Electromagnetic Compatibility, 2015, 57(6): 1529-1538. doi: 10.1109/TEMC.2015.2463814 [7] Nakhla N M, Ruehli A E, Nakhla M S, et al. Simulation of coupled interconnects using waveform relaxation and transverse partitioning[J]. IEEE Trans Components, Packaging and Manufacturing Technology, 2006, 29(1): 78-87. [8] Nakhla N M, Ruehli A E, Nakhla M S, et al. Waveform relaxation techniques for simulation of coupled interconnects with frequency-dependent parameters[J]. IEEE Trans Adv Packag, 2007, 30(2): 257-269. doi: 10.1109/TADVP.2007.896010 [9] Xie Y Z, Guo J, Canavero F G. Analytical iterative solution of electromagnetic pulse coupling to multiconductor transmission lines[J]. IEEE Trans Electromagnetic Compatibility, 2013, 55(3): 451-466. doi: 10.1109/TEMC.2013.2242472 [10] Guo J, Xie Y Z, Canavero F G. Gauss-Seidel iterative solution of electromagnetic pulse coupling to three-conductor transmission lines[J]. IEEE Trans Electromagnetic Compatibility, 2015, 57(2): 292-298. doi: 10.1109/TEMC.2014.2374173 [11] Zhang P F, Du, X L, Zou J, et al. Iterative solution of MTL based on the spatial decomposition and the second-order FDTD[J]. IEEE Trans Magnetics, 2018, 54(3): 1-4. doi: 10.1109/TMAG.2018.2800462 [12] Tesche F M, Ianoz M V, Karlsson T. EMC analysis methods and computational models[M]. New York: John Wiley & Sons, 1997. [13] Agrawal A K. Transient response of multi conductor transmission lines excited by a nonuniform electromagnetic field[J]. IEEE Trans Electromagnetic Compatibility, 1980, 22(2): 119-129. [14] Paul C R. Analysis of multiconductor transmission lines[M]. New York: John Wiley & Sons, 2007. -
点击查看大图
计量
- 文章访问数: 1229
- HTML全文浏览量: 350
- PDF下载量: 84
- 被引次数: 0
