Cavity beam position monitor in laser-driven proton accelerator
-
摘要: 根据激光驱动质子束流低发射度、短脉冲、单束团低电量的性质,研究腔式束流位置探测器(BPM)测量激光加速器产生的质子束团横向位置的可行性问题。针对质子束团的大横向分布和发散角问题,推导了其通过腔式BPM的输出信号,结果表明该信号与集中从束团对称中心、倾斜一定角度通过的束流产生的输出信号相同。依据上述原理,使用CST软件进行了腔式BPM的设计和仿真,确定了矩形谐振腔波导耦合的方案。讨论了该方案的腔式BPM对于激光加速束流的适用性和不同激光驱动质子束流参数的分辨率,并针对PW级激光加速系统进行了分辨率估算。Abstract: According to low-emittance, short-pulse and low-charge-in-single-bunch properties of laser-driven proton beam, we study the feasibility of cavity beam position monitor (BPM) to measure the transverse position of proton beam generated by laser accelerator. In view of the large transverse distribution and divergence angle of proton beam, we derive the output signal when it goes through the cavity BPM, and the result shows that the output signal is identical to that generated by the beam passing through the symmetry center of the transverse distribution and at a certain angle of inclination. Based on the above principle, we use CST software to design and simulate cavity BPM, and determine the scheme of rectangular cavity with coupling waveguide. We discuss the applicability of this scheme for laser-accelerated beam and the resolution of different laser-driven proton beam parameters, and estimate the resolution of PW laser acceleration system.
-
Key words:
- cavity BPM /
- laser-driven proton /
- large transverse distribution /
- divergence angle
-
激光等离子体加速器可以达到TV/m的加速梯度,在极短的距离便可将离子加速到较高能量[1-2],在医用等方向具有重大应用潜力[3],相关应用要求我们必须精准测量束流横向位置。激光驱动质子束流具有短脉冲、低电量等性质,常见于质子装置的BPM,如斜切型BPM[4],shoebox BPM[5]难以满足要求,而电子装置中的腔式BPM[6]具有精确测量低电量束流位置的能力,因此我们探索在激光驱动质子装置中使用腔式BPM的可行性,以期望其实现束流位置的精确测量并伴随激光等离子加速器广泛应用到医疗等领域。本文根据激光驱动质子束流的特点,推导了其通过腔式BPM的输出信号,基于该原理进行了腔式BPM的设计和优化,并讨论了该BPM对于不同激光驱动质子束流的适用性。
1. 腔式BPM对激光驱动质子束流的响应
1.1 腔式BPM的原理
腔式BPM是利用束流经过谐振腔后激励起的偶极模来监测束流的横向位置偏移。以矩形腔的偶极模之一TM210模为例,其电场形式为[7]
{Ex=Ey=0Ez=E0sin(2πax)sin(πby)eiωt (1) 式中: E0为常数,a、b分别为矩形腔的长、短边。考虑一束特征脉宽长度为σt的高斯分布的粒子束,从横向位置(x, y)入射谐振腔,应用近轴条件x=a/2+x′(x′≈0)、y=b/2,有
{RQ0=|V|2ωU≈8LT2ωε0ab(2πa)2x′2∝x′2Vout 0=√ZP=ωq2√ZQext RQ0exp(−ω2σ2t2)∝q|x′| (2) 式中: RQ0为归一化分路阻抗,L为腔体纵向长度,T=sin(ωL/2c)ωL/2c为渡越时间因子,Z为负载特征阻抗,P为输出到负载的功率,q为束团电荷量,Qext为外部品质因数。由此可见在近轴条件下,腔式BPM输出信号幅度Vout0与偏移轴线距离x′成正比,偏移方向则由参考腔提供相位信息进行判断。考虑衰减时间常数τ=QL/ω,则信号形式为
Vout =Vout 0exp(−t2τ)sin(ωt+φ) (3) 式中: QL为有载品质因数,φ为初始相位。
1.2 激光驱动质子束流产生的输出信号
1.2.1 激光驱动质子束流位置偏移的信号
激光加速产生的质子束团具有短脉冲、宽能谱和大散角的特点。因为初始激光打靶的靶点只有μm量级,通常其会具有比较小的发射度,例如内华达大学Cowan等人测量得到的发射度εn, rms~0.004 mm·mrad[8]。在经过束流收集系统收集后, 大散角束流变为小散角束流。因为质子束团有较大的横向面积,所以输出信号必须要考虑束团横向分布的影响。为了得到在较大束斑情况下的信号,我们利用激光驱动质子束团层流的性质[8],将其分割为许多微束(小到可以不计横向分布),叠加所有微束的信号即可得到整体束团的位置信号。此时每个微束由于位置偏移产生的输出信号可以表达为
Vp-bunch =Aqbunch |x|sin(ωt+φ) (4) 式中:A=ω2√ZQext8LT2ωε0ab(2πa)2exp(−ω2σ2t2)exp(−t2τ),qbunch为该微束的电荷量,x为该微束的偏移轴线位置。对所有微束的信号在横向分布条件下加权叠加,即可以得到实际质子束团的输出信号。由于此时所有微束是同时入射进腔式BPM,故在同一侧的束团输出信号同向(φ相等),而在相反两侧的束团输出信号反相(φ相差π),则可以借用偏移位置x的符号来表征相位关系。因此我们考虑相位关系后统一对
Vp-bunch =A1qbun ch x (5) 进行叠加,就可以得到大束斑束团的输出信号, 其中A1=Asin(ωt),并不失一般性取正向入射时φ=0。
为了对微束信号进行加权叠加,我们要得到整个束斑的横向分布。基于北京大学激光等离子体实验室(有目前世界首条且唯一在运行的激光驱动质子束线)的束流实验结果,如图 1所示,发射度约为εn~0.4 mm·mrad,我们做出质子束团的横向分布假设:总电量为Q的束团的横向分布f(x, y)是以位置(x0, y0)为对称中心的中心对称分布,对称中心(x0, y0)定义为大束斑束流的横向偏移位置。此时,叠加所有微束的信号有
Vp-total =∬ (6)  图 1 (a) RCF测得约25%能散束流横向分布,(b)闪烁体测得约4%能散束流横向分布,(c)MCP测得约1%能散束流横向分布Figure 1. Experimental results: (a) beams' transverse distribution with about 25% energy dispersion on RCF, (b) beams' transverse distribution with about 4% energy dispersion on scintillator, and (c) beams' transverse distribution with about 1% energy dispersion on MCP
图 1 (a) RCF测得约25%能散束流横向分布,(b)闪烁体测得约4%能散束流横向分布,(c)MCP测得约1%能散束流横向分布Figure 1. Experimental results: (a) beams' transverse distribution with about 25% energy dispersion on RCF, (b) beams' transverse distribution with about 4% energy dispersion on scintillator, and (c) beams' transverse distribution with about 1% energy dispersion on MCP做变换x=x0+x′,y=y0+y′,则有
\begin{gathered} V_{\mathrm{p} \text {-total }}=\iint_{D^{\prime}} A_1 Q f\left(x_0+x^{\prime}, y_0+y^{\prime}\right)\left(x_0+x^{\prime}\right) \mathrm{d} s^{\prime}=A_1 Q x_0 \iint_{D^{\prime}} f\left(x_0+x^{\prime}, y_0+y^{\prime}\right) \mathrm{d} s^{\prime}+ \\ A_1 Q \iint_{D^{\prime}} f\left(x_0+x^{\prime}, y_0+y^{\prime}\right) x^{\prime} \mathrm{d} s^{\prime}=A_1 Q x_0 \quad\left(x^{\prime}, y^{\prime}\right) \in D^{\prime} \end{gathered} (7) 其中 \iint_{D^{\prime}} f\left(x_0+x^{\prime}, y_0+y^{\prime}\right) \mathrm{d} s^{\prime}为分布函数平移后的积分,值仍为1, \iint_{D^{\prime}}\left(f\left(x_0+x^{\prime}, y_0+y^{\prime}\right) x^{\prime} \mathrm{d} s^{\prime}\right.为二元偶函数与奇函数的乘积在对称定义域上的积分,值为0。因此可以得出,虽然束斑横向面积较大,如果其横向分布满足关于某点(x0, y0)中心对称时,其入射进腔式BPM产生的输出信号等价于相同电量的微束从点(x0, y0)入射进腔式BPM产生的输出信号。
1.2.2 激光驱动质子束流发散角的信号
为了得到质子束团发散角的输出信号,我们仍将其分割为许多微束(小到可以不计横向分布),则叠加所有微束倾斜入射产生的信号即为发散角的信号。激光驱动质子束团在经过收集系统后,散角变小,所有微束均满足较小的倾斜角条件(tanθ≈θ),则微束倾斜θ入射产生的信号可以表示为[7]
V_{\text {a-bunch }}=A_2 q_{\text {bunch }} \theta (8) 式中: A_2=\frac{\omega}{2} \sqrt{\frac{Z}{Q_{\mathrm{ext}}} \frac{8 T^2}{\omega \varepsilon_0 a b}\left(\frac{2 {\rm{ \mathsf{ π} }}}{a}\right)^2} \frac{L}{2} \sqrt{\frac{L}{2}} \sin \left(\frac{\omega L}{4 c}\right) \exp \left(-\frac{\omega^2 \sigma_t{ }^2}{2}\right) \exp \left(-\frac{t}{2 \tau}\right) \cos (\omega t),其中已由θ的符号表征不同倾斜角入射后的信号之间相位关系(同相或反相),并且比较A1和A2的振荡项可知位置信号与倾斜信号相位正交(π/2相差)。
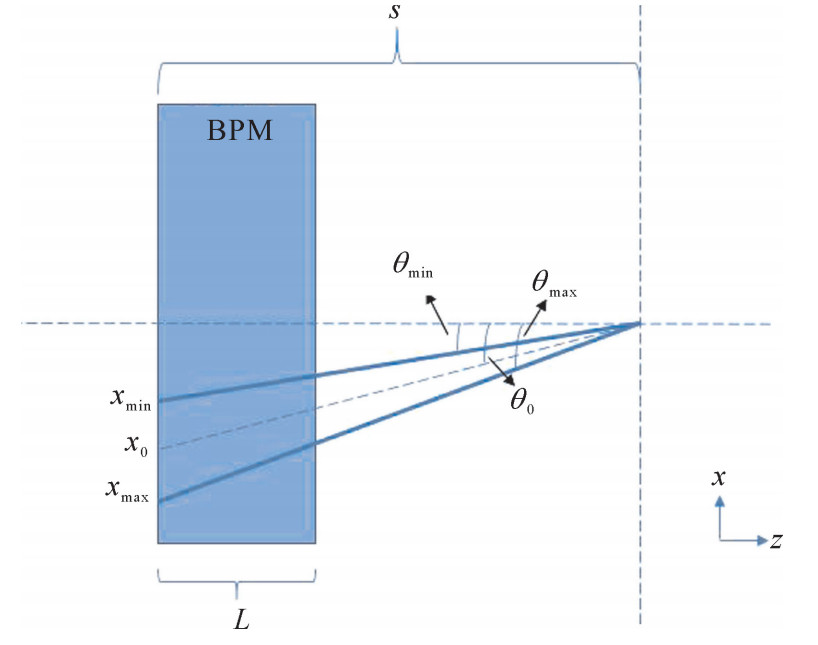
为了对各倾斜微束信号进行加权叠加,我们要得到整个束斑的倾斜角分布。束团倾斜入射进腔式BPM的轨迹在x-z平面的投影如图 2,其中s为聚焦时的某个固定距离。根据上小节中束团横向分布关于点(x0, y0)中心对称的假设有
f\left(x_0-x\right)=f\left(x_0+x\right) (9) 再依据激光驱动质子束团小倾斜角条件(tanθ≈θ)有
f\left(s \theta_0-s \theta\right)=f\left(s \theta_0+s \theta\right) (10) 即束团的倾斜角分布g(θ)=f(sθ) 为关于角θ0的对称分布。此时,叠加所有微束的倾斜信号有
V_{\text {a-total }}=\int_{\theta_{\min }}^{\theta_{\max }} A_2 Q g(\theta) \theta \mathrm{d} \theta (11) 做类似上小节的变换,最终可以得到Va-total=A2Qθ0。因此可以得出,得益于激光驱动质子束团较小的发射度,在束团横向分布中心对称假设下,其入射进腔式BPM后由于发散角产生的输出信号等价于相同电量的微束倾斜θ0入射时产生的输出信号。
综合位置信号和发散角信号,合输出信号为
V_{\text {total }}=V_{\mathrm{p} \text {-total }}+\mathrm{j} V_{\mathrm{a} \text {-total }} (12) 两信号之间正交(存在π/2相差),故通过相位探测可以分别获得对应信号。通过上述推导,我们证明了在腔式BPM中中心对称束流以小发散角入射与微束倾斜入射的等价性,继而实现了可以利用微束来模拟设计应用于激光驱动质子束流的腔式BPM。
2. 腔式BPM设计
2.1 腔式BPM的参数设计及仿真
为了防止信号串扰[9],我们采用矩形谐振腔方案[10]。考虑到质子束流横向尺寸大,需要在大谐振腔上开足够大的管道直径,我们将工作频率选定为f210=1.32 GHz和f120=1.42 GHz。根据理想矩形谐振腔本征模频率公式
f_{\text {m n } \mathrm{p}}=\frac{c}{2} \sqrt{\left(\frac{m}{a}\right)^2+\left(\frac{n}{b}\right)^2+\left(\frac{p}{l}\right)^2}, \quad m n \neq 0 (13) 得到腔体长边a=260.84 mm,短边b=230.86 mm。使用CST微波模块进行本征模仿真得到矩形腔两个偶极模的磁场如图 3。
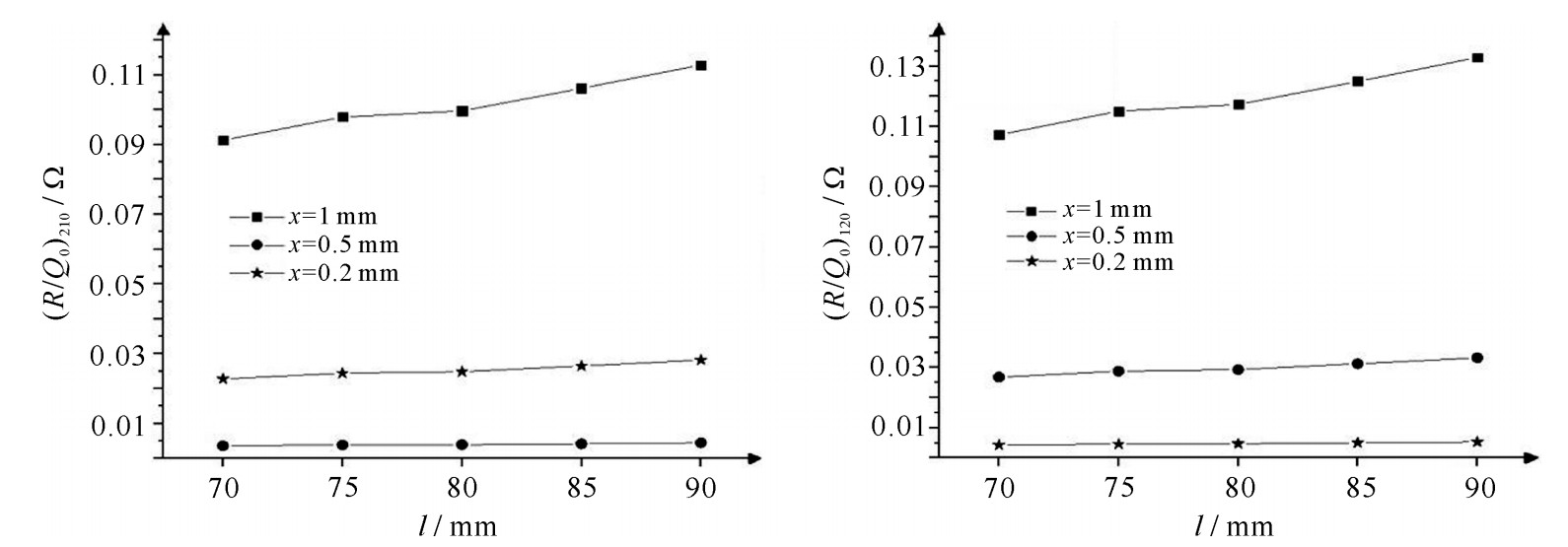
接下来,我们不断调整腔体的长度L和管道直径D,来仿真式(2)中的归一化分路阻抗 \frac{R}{Q_0}。当D=80 mm时,改变L分别得到的两个偶极模在不同位置处的 \frac{R}{Q_0},如图 4。同时不断调整波导和同轴耦合件参数,来仿真优化式(2)中的外部品质因数Qext,使两个模式的Qext均为2000左右。
由于对谐振腔的开孔等因素,本征模频率会出现漂移。我们通过微调腔体及波导位置等将频率修正回设计值,最终腔式BPM优化尺寸如表 1所示,其中波导采用标准波导BJ-18型,其位置指波导边缘距离谐振腔中轴线距离。腔式BPM的理论参数如表 2所示,其中 \frac{R}{Q_0}为1 mm处归一化分路阻抗。
表 1 腔式BPM优化尺寸Table 1. Optimum geometry of cavity BPMa /mm b/mm L/mm D/mm waveguide length X/mm waveguide position X/mm waveguide length Y/mm waveguide position Y/mm 241.6 210 75 80 250 90.5 280 76 表 2 腔式BPM理论参数Table 2. Theoretical parameters of cavity BPMf110/GHz (R/Q0)110/Ω f210/GHz (Qext)210 (R/Q0)210/Ω f120/GHz (Qext)120 (R/Q0)120/Ω 0.9167 224.5 1.320 1955 0.1088 1.420 2103 0.1328 2.2 适用范围讨论及分辨率估计
激光驱动质子束流初始能谱宽,经过束线选能后不同能量的束团电量可达到几十pC到nC不等[11-12],其脉宽σt主要由中心能量E、能散Δ及传输距离s决定,可以估算为
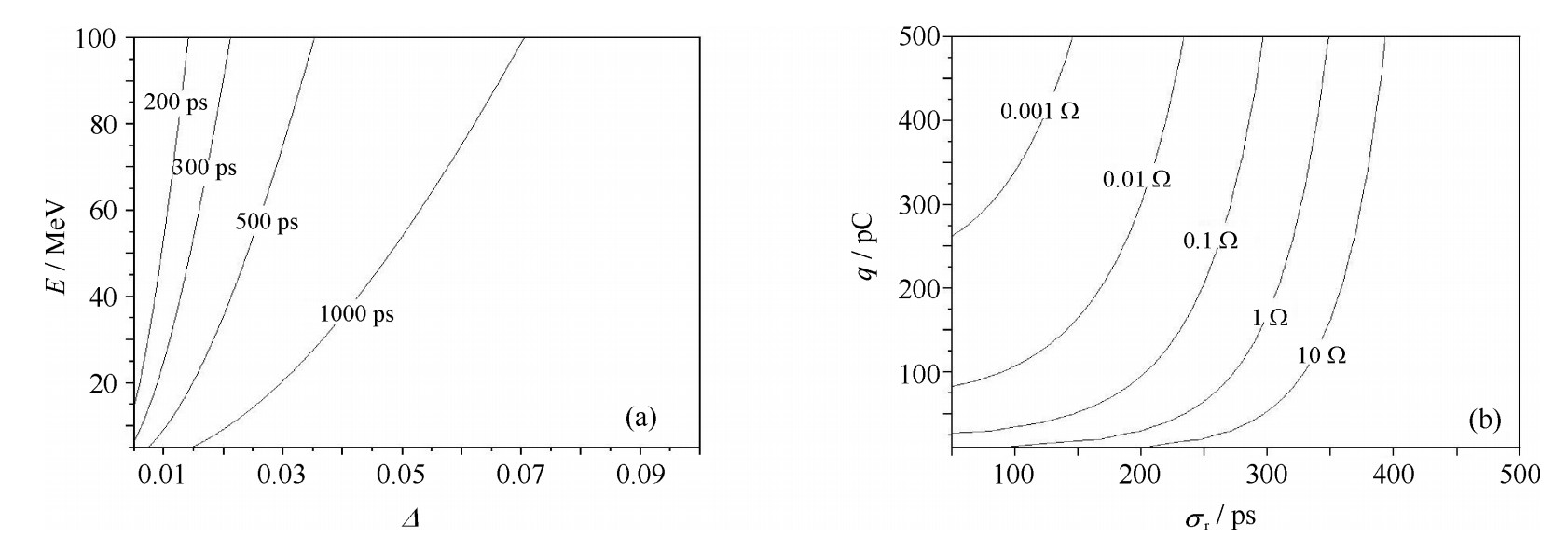
\begin{aligned} &\sigma_t \approx \frac{1}{2.3556} \frac{s}{v_2-v_1} \approx \\ &\frac{1}{2.3556} \frac{s}{c}\left(1 / \sqrt{1-\left(\frac{\varepsilon_0}{\varepsilon_0+E(1-{\mathit{\Delta}} / 2)}\right)^2}-1 / \sqrt{1-\left(\frac{\varepsilon_0}{\varepsilon_0+E(1+{\mathit{\Delta}} / 2)}\right)^2}\right) \end{aligned} (14) 式中: 2.355 6为高斯分布半高宽与特征脉宽σt的比例常数,v2, v1为正负最大能散处速度,ε0为质子静止能量,取s=10 m处,代入激光驱动质子束流的能量及能散信息可获得脉宽分布如图 5(a)。进一步,将式(2)变化得到极限分辨率处归一化分路阻抗表达式
\frac{R}{Q_0}=\left(\frac{2 V_{\text{out} 0}}{\omega q \exp \left(-\frac{\omega^2 \sigma_{\mathrm{t}}^2}{2}\right)}\right)^2 \frac{Q_{\text {ext }}}{Z} (15) 由于存在暗电流等干扰,参考文献[10]中的测量值,在分辨率极限处至少应有Vout0=5 mV,同时取Z=50 Ω,代入激光驱动质子束流的电量和脉宽信息可得 \frac{R}{{{Q_0}}}的分布如图 5(b),与图 3中各位置处 \frac{R}{{{Q_0}}}值比较可以得到不同激光驱动质子束团条件下能达到的位置分辨率。
以目前PW级激光加速系统的典型质子加速结果[11]为例进行分辨率预估,得到表 3, 其中σt为束团按1%能散传输10 m时的脉宽,结果表明对于不同能量束团可实现好于1 mm的位置分辨率。
表 3 分辨率估计Table 3. Resolution estimationE/MeV σt/ps q/pC (R/Q0)210/Ω resolution/mm 30 273 500 0.039 2 0.6 50 208 150 0.050 7 0.8 100 142 50 0.093 2 1 3. 结论
本文推导了应用于激光驱动质子束流的腔式BPM的输出信号,证明了当束流横向分布满足关于点(x0, y0) 中心对称分布、束团发散角较小时,其产生的输出信号等价于同电量微束从点(x0, y0) 倾斜θ0入射进腔式BPM时产生的输出信号。基于这个原理,我们使用CST软件进行了应用在激光驱动质子装置上的腔式BPM的设计仿真,采用了矩形腔波导耦合的方案,且选择的工作频率较低、间隔较大,最大限度防止信号串扰。对本腔式BPM在不同激光驱动质子束团参数条件下可获得的分辨率进行了讨论,结果表明其应用在PW激光加速系统中可以实现较好的位置分辨率。
-
图 1 (a) RCF测得约25%能散束流横向分布,(b)闪烁体测得约4%能散束流横向分布,(c)MCP测得约1%能散束流横向分布
Figure 1. Experimental results: (a) beams' transverse distribution with about 25% energy dispersion on RCF, (b) beams' transverse distribution with about 4% energy dispersion on scintillator, and (c) beams' transverse distribution with about 1% energy dispersion on MCP
表 1 腔式BPM优化尺寸
Table 1. Optimum geometry of cavity BPM
a /mm b/mm L/mm D/mm waveguide length X/mm waveguide position X/mm waveguide length Y/mm waveguide position Y/mm 241.6 210 75 80 250 90.5 280 76 表 2 腔式BPM理论参数
Table 2. Theoretical parameters of cavity BPM
f110/GHz (R/Q0)110/Ω f210/GHz (Qext)210 (R/Q0)210/Ω f120/GHz (Qext)120 (R/Q0)120/Ω 0.9167 224.5 1.320 1955 0.1088 1.420 2103 0.1328 表 3 分辨率估计
Table 3. Resolution estimation
E/MeV σt/ps q/pC (R/Q0)210/Ω resolution/mm 30 273 500 0.039 2 0.6 50 208 150 0.050 7 0.8 100 142 50 0.093 2 1 -
[1] Schwoerer H, Pfotenhauer S, Jäckel O, et al. Laser-plasma acceleration of quasi-monoenergetic protons from microstructured targets[J]. Nature, 2006, 439(7075): 445-448. doi: 10.1038/nature04492 [2] Snavely R A, Key M H, Hatchett S P, et al. Intense high-energy proton beams from petawatt-laser irradiation of solids[J]. Physical Review Letters, 2000, 85(14): 2945-2948. doi: 10.1103/PhysRevLett.85.2945 [3] Tajima T, Habs D, Yan X Q. Laser acceleration of ions for radiation therapy[J]. Reviews of Accelerator Science and Technology, 2009, 2(01): 201-228. doi: 10.1142/S1793626809000296 [4] 毕宏宇, 徐韬光, 傅世年. 中国散裂中子源快循环同步加速器环斜切型束流位置探测器设计[J]. 原子能科学技术, 2011, 45(5): 600-605. https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201105018.htmBi Hongyu, Xu Taoguang, Fu Shinian. Design of linear-cut beam position monitor in rapid cycling synchrotron of China spallation neutron source. Atomic Energy Science and Technology, 2011, 45(5): 600-605 https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201105018.htm [5] Wang M W, Zhen S X, Zhang H Y, et al. Development of Shoebox BPM for Xi'an Proton Application Facility[C]//Proceedings of IPAC2016. 2016: 175-177. [6] Walston, S, Boogert, S, Chung, C, et al. Performance of a high resolution cavity beam position monitor system[J]. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 2007, 578(1): 1-22. [7] Tomoya Nakamura. Development of beam-position monitors with high position resolution[D]. Tokyo: The University of Tokyo, 2008. [8] Cowan, T E, Fuchs J, Ruhl H, et al. Ultralow emittance, multi-MeV proton beams from a laser virtual-cathode plasma accelerator[J]. Physical Review Letters, 2004, 92: 204801. doi: 10.1103/PhysRevLett.92.204801 [9] Sargsyan V. Cross-talk problem in pill-box cavity[R]. TESLA Report 2003-01, 2003. [10] 李享. 腔式束流位置检测器的设计与实验[D]. 北京: 清华大学, 2009.Li Xiang. Design and experiments for cavity beam position monitor. Beijing: Tsinghua University, 2009 [11] Kim I J, Pae K H, Choi I W, et al. Radiation pressure acceleration of protons to 93 MeV with circularly polarized petawatt laser pulses[J]. Physics of Plasmas, 2016, 23: 070701. doi: 10.1063/1.4958654 [12] Liao Q, Wu M J, Gong Z, et al. Enhanced laser proton acceleration by target ablation on a femtosecond laser system[J]. Physics of Plasmas, 2018, 25: 063109. doi: 10.1063/1.5025239 -





 下载:
下载:





 下载:
下载: