基于模态匹配法的接触刚度

王梓豪; 李春华; 王之琢; 王海静; 屈化民

doi:10.11884/HPLPB201931.190033

基于模态匹配法的接触刚度

doi: 10.11884/HPLPB201931.190033

王梓豪^{1, 2,},
李春华¹,
王之琢^{1, 2},
王海静¹,
屈化民¹

1.
中国科学院高能物理研究所, 北京 100049
2.
中国科学院大学, 北京 100049

基金项目:

国家重大科学基础设施项目发改高技[2018]1928号

详细信息

作者简介:
王梓豪(1989-), 男, 博士, 从事加速器机械结构设计及振动方面研究, wangzihao@ihep.ac.cn

中图分类号: TL503
计量
- 文章访问数: 1349
- HTML全文浏览量: 360
- PDF下载量: 63
- 被引次数: 0
出版历程
- 收稿日期: 2019-01-24
- 修回日期: 2019-04-09
- 刊出日期: 2019-08-15

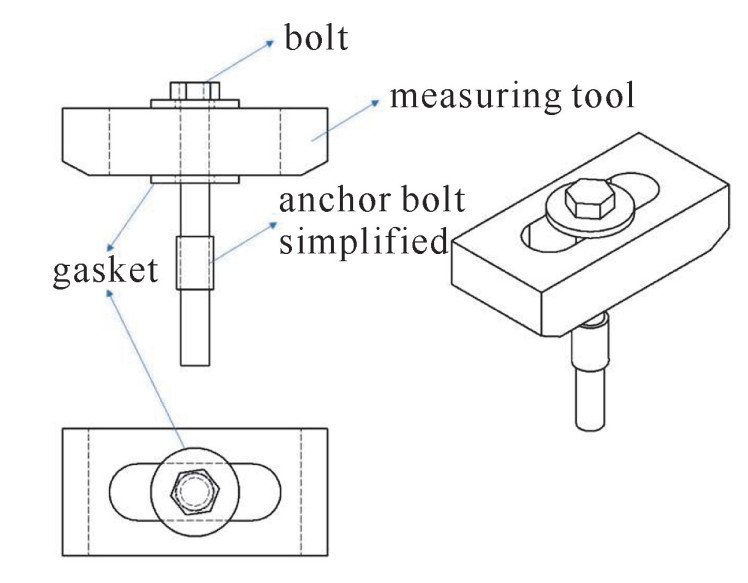
Contact stiffness measurement based on modal matching method

1.
Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China

摘要

摘要: 提出一种间接测量平面接触刚度的方法，准确量化粗糙表面的接触刚度，使得整个支架系统的固有频率模拟与测试结果得到良好的匹配。基于接触刚度模型、ANSYS有限元模拟方法以及模态测试方法，以地脚螺栓固定方式的测试件为例，验证了间接测量方法的准确性，使接触刚度得到准确量化。该方法可以为提高加速器磁铁支架系统的整体刚度提供依据。
- 磁铁支架 /
- 接触刚度 /
- 模态测试 /
- ANSYS有限元分析 /
- 模态匹配
Abstract: In the simulation of the accelerator magnet support system, the parts connected to the ground by the magnet bracket are usually treated as “fixed”, but in some cases, this treatment will cause a large error between the simulation results and the measurement results. This paper proposes an indirect method to measure the contact stiffness of rough surface, accurately quantify the contact stiffness of rough surface, and make the simulation of the whole system well match with the test results. Based on the contact stiffness model, ANSYS finite element simulation method and modal test method, the accuracy of indirect measurement method was verified by taking the test piece of anchor bolt fixation method as an example, so that the contact stiffness was accurately quantified. This method can also provide a basis for improving the overall stiffness of the accelerator magnet support system.
- magnet support /
- contact stiffness /
- modal testing /
- ANSYS finite element analysis /
- modal matching method

HTML全文

图 1 测试件结构示意图

Figure 1. Schematic diagram of test-piece structure

下载: 全尺寸图片幻灯片

图 2 试验地面

Figure 2. Test site

下载: 全尺寸图片幻灯片

图 3 测量工具示意图

Figure 3. Schematic diagram of measurement tool

下载: 全尺寸图片幻灯片

图 4 测量工具模态测试结果振型图

Figure 4. Vibration mode of measurement tool

下载: 全尺寸图片幻灯片

图 5 测量工具模态测试结果频响函数曲线

Figure 5. Frequency response function curves of modal test results

下载: 全尺寸图片幻灯片

图 6 测量工具模型俯视图

Figure 6. Top view of measurement tool model

下载: 全尺寸图片幻灯片

图 7 P1第一阶模态结果修正过程曲线

Figure 7. Correction process curve of the first mode results of P1

下载: 全尺寸图片幻灯片

图 8 测试件模态测试振型

Figure 8. Vibration mode of test-piece

下载: 全尺寸图片幻灯片

图 9 测试件模态分析结果振型图

Figure 9. Modal analysis results of test-piece

下载: 全尺寸图片幻灯片

图 10 HEPS-TF磁铁支架

Figure 10. HEPS-TF magnet support

下载: 全尺寸图片幻灯片

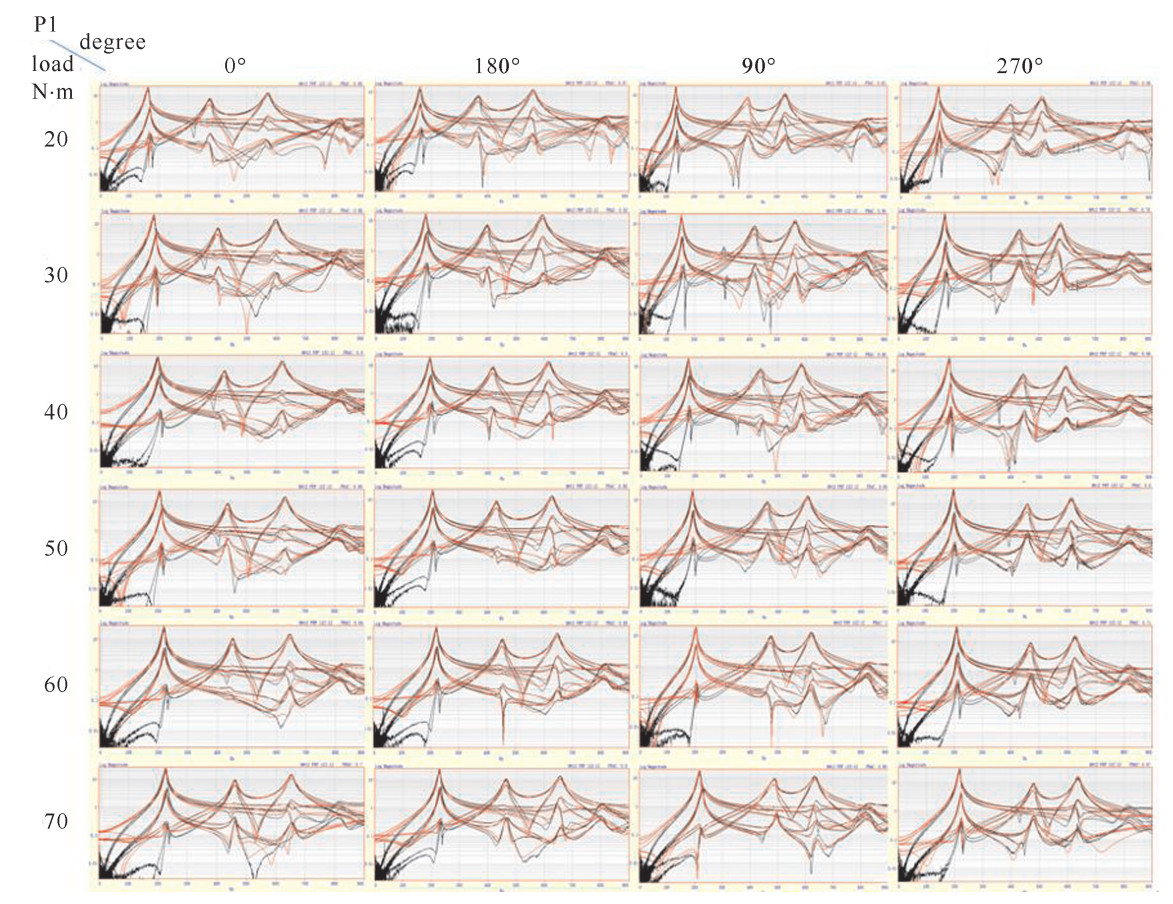
表 1 固有频率测试结果

Table 1. Natural frequency test results

natural frequency/Hz
load/(N·m)	a=0°			a=180°			a=90°			a=270°
load/(N·m)	1^st order	2^nd order	3^rd order	1^st order	2^nd order	3^rd order	1^st order	2^nd order	3^rd order	1^st order	2^nd order	3^rd order
20	162	373	570	161	368	561	134	391	528	135	393	505
30	179	399	596	179	396	592	154	418	564	166	431	575
40	195	421	618	193	416	613	175	439	586	181	444	593
50	203	435	630	206	431	627	190	460	605	198	457	612
60	217	451	644	220	452	645	200	472	620	208	469	626
70	225	461	652	228	464	655	216	484	633	216	478	635

下载: 导出CSV

表 2 接触参数

Table 2. Contact parameters

orientation	load/(N·m)	A_n/(10^-3m²)	P_i	E/10¹⁰Pa	W_t*/10^－4	h^*	K_t*/10^－4	σ/10^-9m	K_t/(10¹³N·m^-1)
	20				1.19	1.46	1.95		0.647
0°	40	1.58	0.7	2.56	2.38	1.08	3.12	1.22	1.03
	60				3.56	0.833	4.04		1.34
	20				1.19	1.46	1.95		0.647
180°	40	1.58	0.7	2.56	2.38	1.08	3.12	1.22	1.03
	60				3.56	0.833	4.04		1.34
	20				1.19	1.46	1.95		0.647
90°	40	1.58	0.7	2.56	2.38	1.08	3.12	1.22	1.03
	60				3.56	0.833	4.04		1.34
	20				1.19	1.46	1.95		0.647
270°	40	1.58	0.7	2.56	2.38	1.08	3.12	1.22	1.03
	60				3.56	0.833	4.04		1.34

下载: 导出CSV

表 3 测试件模拟结果与测量结果前四阶固有频率数值对比

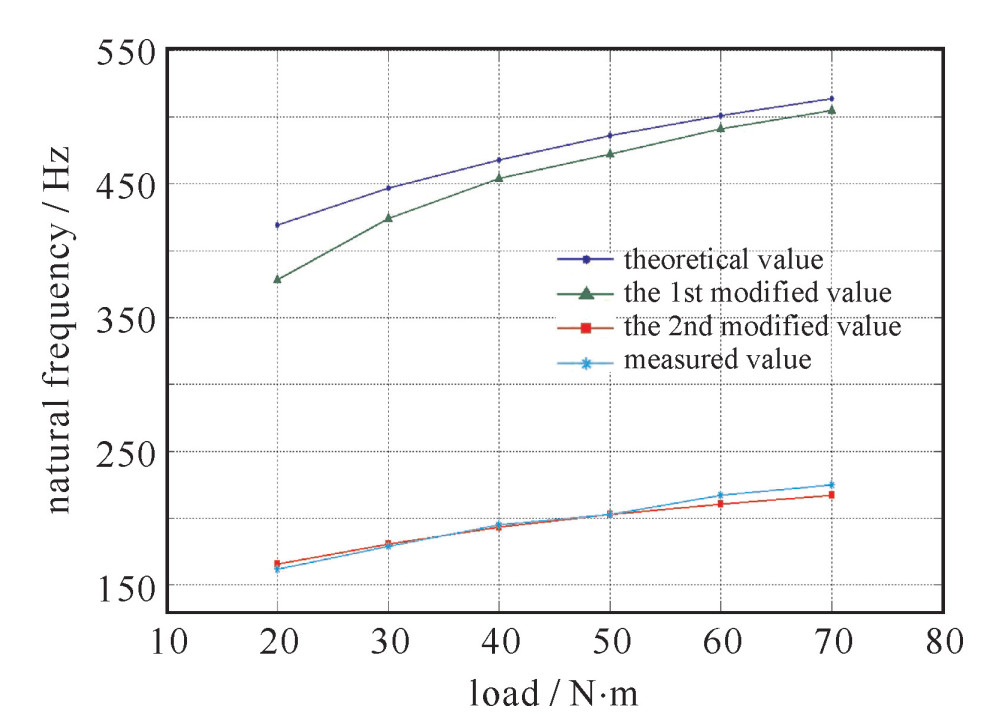
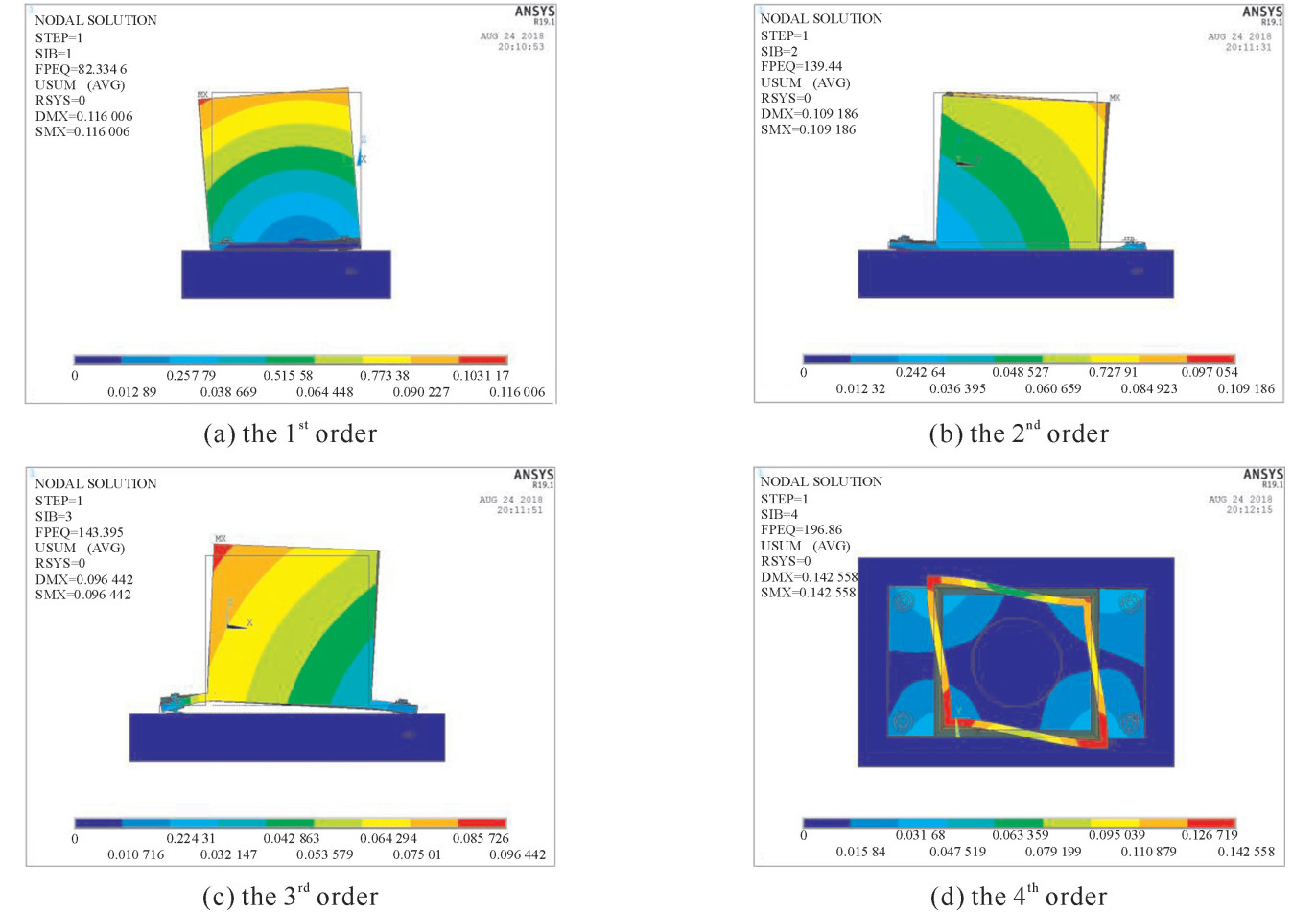
Table 3. Comparison of natural frequencies

test	load/(N·m)	simulated natural frequency/Hz				measured natural frequency/Hz				error
test	load/(N·m)	1^st order	2^nd order	3^rd order	4^th order	1^st order	2^nd order	3^rd order	4^th order	1^st order	2^nd order	3^rd order	4^th order
1	20	70	125	131	190	86	144	152	194	18%	13%	14%	2%
2	30	82	139	143	197	92	159	171	196	11%	12%	16%	0%
3	40	88	147	151	200	103	150	165	190	15%	2%	9%	5%
4	50	91	151	154	202	105	150	168	194	14%	1%	8%	4%
5	60	93	155	159	204	107	151	171	195	13%	3%	7%	5%
6	70	95	158	161	205	108	150	174	195	12%	5%	7%	5%
7	80	96	160	163	206	109	173	182	196	12%	7%	10%	5%
8	90	98	162	165	207	109	150	182	197	10%	8%	9%	5%
9	100	98	163	167	208	110	150	181	197	10%	9%	8%	5%
10	110	99	164	168	208	112	155	182	199	11%	6%	8%	5%
11	-	176	267	275	288	-	-	-	-	57%	72%	51%	45%

下载: 导出CSV

表 4 不同约束方式模拟结果对比

Table 4. Comparison of simulation results

	constraint way	natural frequency/Hz		error
		1st	2nd	1st	2nd
measurement		63.5	95.6
	contact	71.6	95.9	12.8%	0.3%
simulation	partially fixed	98	101	54.3%	5.6%
	fixed	296	312	366.1%	226.4%

下载: 导出CSV

表 5 测量和模拟结果对比

Table 5. Comparison of measurement and simulation results

simulation natural frequency/Hz		measurement natural frequency/Hz		error
1st	2nd	1st	2nd	1st	2nd
25.6	29.6	24.4	27.4	4.9%	8.0%

下载: 导出CSV

参考文献(15)

[1]	Preissner C, Cease H, Collins J, et al. Nostradamus and the synchrotron engineer: Key aspects of predicting accelerator structural response[C]//International Conference on Mechanical Engineering Design of Synchrotron Radiation Equipment and Instrumentation. 2016: 272-276.
[2]	Nudell J, Liu Z, Preissner C, et al. Preliminary design and analysis of the FODO module support system for the APS-U storage ring[C]//International Conference on Mechanical Engineering Design of Synchrotron Radiation Equipment and Instrumentation. 2016: 83-86.
[3]	Cianciosi F, Brochard T, Marion P, et al. The girder system for the new ESRF storage ring[C]//International Conference on Mechanical Engineering Design of Synchrotron Radiation Equipment and Instrumentation. 2016: 147-151.
[4]	陈学前, 沈展鹏, 刘信恩, 等. 地脉动环境下反射镜架系统的镜片转角响应计算[J]. 强激光与粒子束, 2018, 30: 072001. doi: 10.11884/HPLPB201830.170529 Chen Xueqian, Shen Zhanpeng, Liu Xin'en, et al. Analysis on rotation angle of mirror in reflector system under ground random vibration. High Power Laser and Particle Beams, 2018, 30: 072001 doi: 10.11884/HPLPB201830.170529
[5]	王坤, 何静, 游安清. 光束-靶面入射角非接触式测量方法分析[J]. 强激光与粒子束, 2014, 26: 101010. doi: 10.11884/HPLPB201426.101010 Wang Kun, He Jing, You Anqing. Analysis on non-contact measurement of ray-target incident angle. High Power Laser and Particle Beams, 2014, 26: 101010 doi: 10.11884/HPLPB201426.101010
[6]	张敏, 赵平, 张蓉. 气浮隔振平台模态实验分析[J]. 强激光与粒子束, 2013, 25(S0): 87-90. http://www.hplpb.com.cn/article/id/7799 Zhang Min, Zhao Ping, Zhang Rong. Application of black-box testing technologies to command and control subsystem software testing. High Power Laser and Particle Beams, 2013, 25(S0): 87-90 http://www.hplpb.com.cn/article/id/7799
[7]	杨航, 汪玉兰, 汪雪, 等. 精密热处理过程温度测量多模态重构方法[J]. 强激光与粒子束, 2019, 31: 012003. doi: 10.11884/HPLPB201931.180060 Yang Hang, Wang Yulan, Wang Xue, et al. Multimodal reconstruction method of precision heat treatment process's temperature measurement. High Power Laser and Particle Beams, 2019, 31: 012003 doi: 10.11884/HPLPB201931.180060
[8]	田小龙, 王雯, 傅卫平, 等. 考虑微凸体相互作用的机械结合面接触刚度模型[J]. 机械工程学报, 2017, 53(17): 149-159. Tian Xiaolong, Wang Wen, Fu Weiping, et al. Contact stiffness model of mechanical joint surfaces considering the asperity interactions. 2017, 53(17): 149-159
[9]	Greenwood J, Williamson J. Contact of nominally flat surfaces[J]. Proceedings of the Royal Society, 1966, 295(42): 300-319.
[10]	Chang W, Etsion I, Bogy D. An elastic-plastic model for the contact of rough surfaces[J]. Journal of Tribology, 1987, 109(2): 257-263. doi: 10.1115/1.3261348
[11]	Zhao Yongwu, Maietta D, Chang Liang. An asperity microcontact model incorporating the transition from elastic deformation to fully plastic flow[J]. Journal of Tribology, 1999, 122(1): 86-93.
[12]	Zhao Yongwu, Chang Liang. A model of asperity interactions in elastic-plastic contact of rough surfaces[J]. Journal of Tribology, 2000, 123(4): 857-864. https://pennstate.pure.elsevier.com/en/publications/a-model-of-asperity-interactions-in-elastic-plastic-contact-of-ro
[13]	Kogut L, Etsion I. A finite element based elastic-plastic model for the contact of rough surfaces[J]. Tribology Transactions, 2003, 46(3): 383-390. doi: 10.1080/10402000308982641
[14]	Nuri K, Halling J. The normal approach between rough flat surfaces in contact[J]. Wear, 1975, 32(1): 81-93. https://www.sciencedirect.com/science/article/pii/0043164875902069
[15]	WangHaijing, Li Chunhua, Zhu Hongyan, et al. Test of magnet girder prototypes for HEPS-TF[C]//International Particle Accelerator Conference. 2018: 76-79.