基于宽频带温度脉动仪的大气温度起伏谱测量

任鹏飞; 崔朝龙; 刘庆; 黄宏华

doi:10.11884/HPLPB201931.190048

基于宽频带温度脉动仪的大气温度起伏谱测量

doi: 10.11884/HPLPB201931.190048

任鹏飞^{1, 2,},
崔朝龙¹,
刘庆¹,
黄宏华^1, ,

1.
中国科学院安徽光学精密机械研究所中国科学院大气光学重点实验室, 合肥 230031
2.
中国科学技术大学研究生院科学岛分院, 合肥 230026

基金项目:

中国科学院战略性先导科技转型(A类) 基金项目 XDA17010104

详细信息

作者简介:
任鹏飞(1993-), 男, 硕士研究生, 主要从事对流湍流池的研制及实验研究, siwuxie1@mail.ustc.edu.cn

通讯作者:
黄宏华(1976-), 男, 研究员, 主要从事大气光学参数特性、湍流图像传输研究, hhhuang@aiofm.ac.cn

中图分类号: TN246
计量
- 文章访问数: 1229
- HTML全文浏览量: 345
- PDF下载量: 115
- 被引次数: 0
出版历程
- 收稿日期: 2019-02-22
- 修回日期: 2019-04-14
- 刊出日期: 2019-08-15

Measurements of the spectrum of atmospheric temperature fluctuations based on broadband micro-temperature sensor

Ren Pengfei^{1, 2
,},
Cui Chaolong¹,
Liu Qing¹,
Huang Honghua^{1
, ,}

1.
Key Laboratory of Atmospheric Optics, Anhui Institute of Optics and Fine Mechanics, Chinese Academy of Sciences, Hefei 230031, China
2.
Science Island Branch of Graduate School, University of Science and Technology of China, Hefei 230026, China

摘要

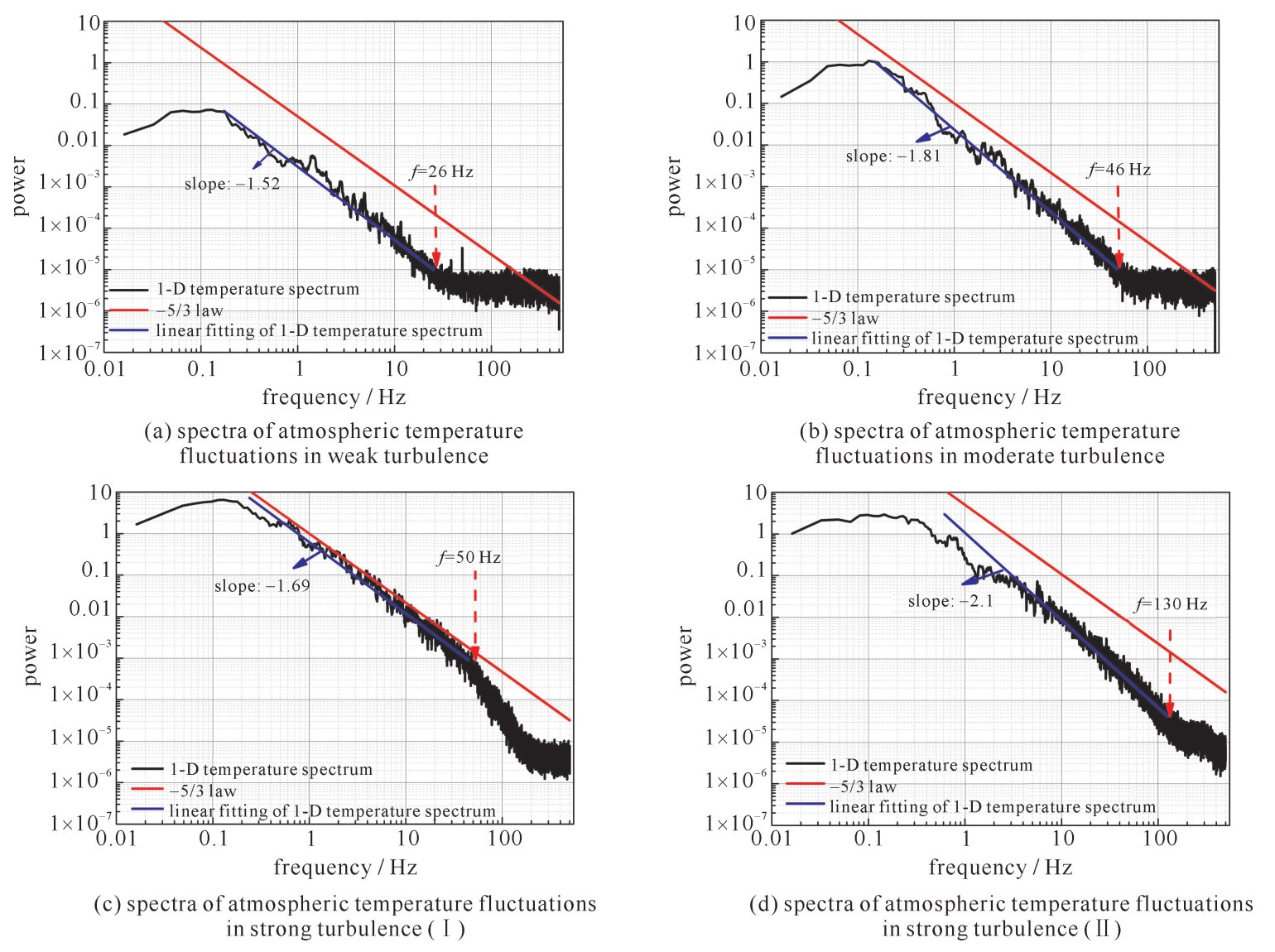
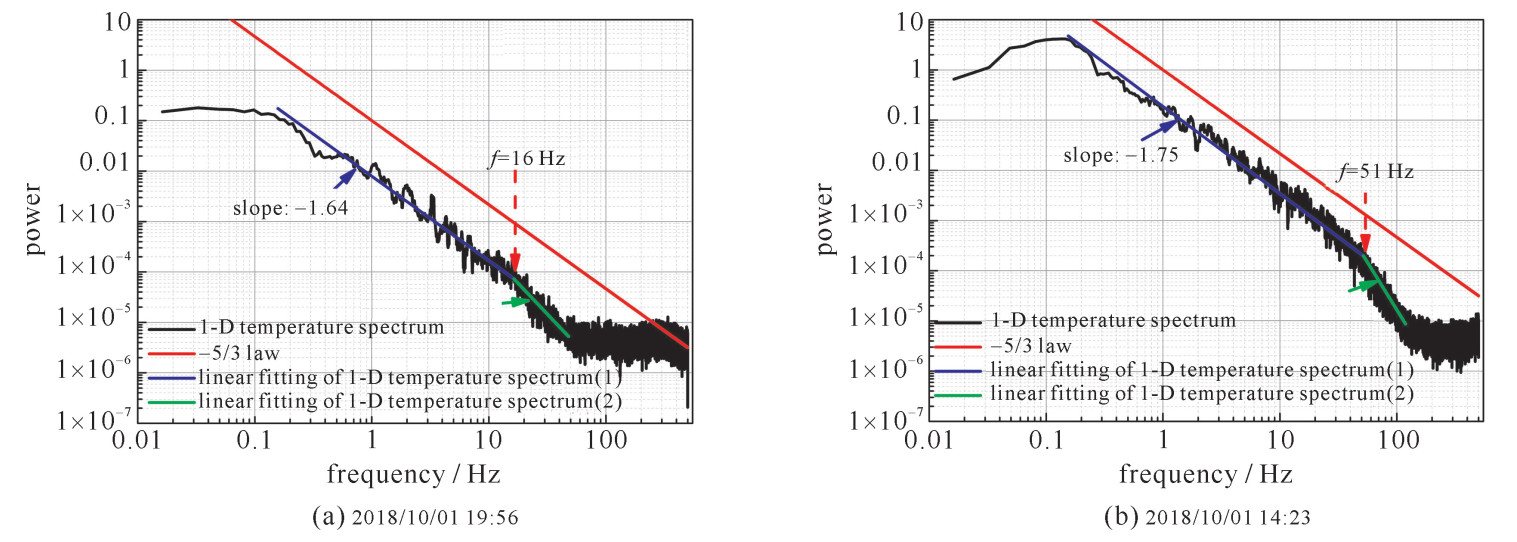
摘要: 常用温度脉动仪测量湍流的频谱, 频谱范围多在20Hz以下, 无法呈现大气温度起伏的高频特征。介绍一种宽频带低噪声温度脉动仪的设计方法, 研制出相应的仪器, 并进行了真实大气温度起伏测量实验。结果表明, 大气温度起伏具有丰富的高频信息, 温度起伏功率谱在更宽的频率范围内存在幂率不变性, 部分温度谱在高频部分出现拐点, 以更陡的幂率下降, 湍流谱的形状以及拐点出现的位置和湍流强度有一定的关系。拓宽了温度起伏功率谱的研究范围, 为光波传输的理论研究和技术应用提供了高频湍流谱信息, 为非Kolmogorov湍流研究提供了测量手段。
- 温度脉动仪 /
- 宽频带 /
- 湍流 /
- 温度起伏
Abstract: The frequency spectrum of turbulence measured by common micro-temperature sensor is mostly below 20 Hz, which can not show the high frequency characteristics of atmospheric temperature fluctuation.This paper introduces the design of a broadband low noise micro-temperature sensor, the development of the corresponding instrument, and the real atmospheric temperature fluctuation measurement experiment.It is shown that the atmospheric temperature fluctuation has abundant high frequency information.The power spectrum of temperature fluctuation has power invariance in a wider frequency range.Some of the temperature spectrum has inflection points in the high frequency part, and decreases more steeply.The shape of the turbulence spectrum and the position of the inflection point are related to the turbulence intensity.This study broadens the research scope of temperature fluctuation power spectrum, provides high frequency turbulence spectrum information for theoretical research and technical application of light wave transmission, and provides measurements for non-Kolmogorov turbulence research.
- micro-temperature sensor /
- broadband /
- turbulence /
- temperature fluctuation

HTML全文

图 1 信号采集放大电路

Figure 1. Acquisition and amplification circuit

下载: 全尺寸图片幻灯片

图 2 微弱信号检测

Figure 2. Weak signal detection

下载: 全尺寸图片幻灯片

图 3 系统噪声

Figure 3. System noise

下载: 全尺寸图片幻灯片

图 4 不同湍流强度下的大气温度起伏谱

Figure 4. The spectra of atmospheric temperature fluctuations in different turbulences

下载: 全尺寸图片幻灯片

图 5 直径6 μm温度谱幂率统计(0.1~35 Hz)

Figure 5. Probability distributions of power law measurements with 6 μm tungsten wire

下载: 全尺寸图片幻灯片

图 6 高频部分有拐点的大气温度起伏谱

Figure 6. Atmospheric temperature fluctuation spectra with inflection point in high frequency

下载: 全尺寸图片幻灯片

表 1 钨丝参数(293 K, 2 m/s，10⁵ Pa)

Table 1. Parameters of tungsten wire(293 K, 2 m/s, 10⁵ Pa)

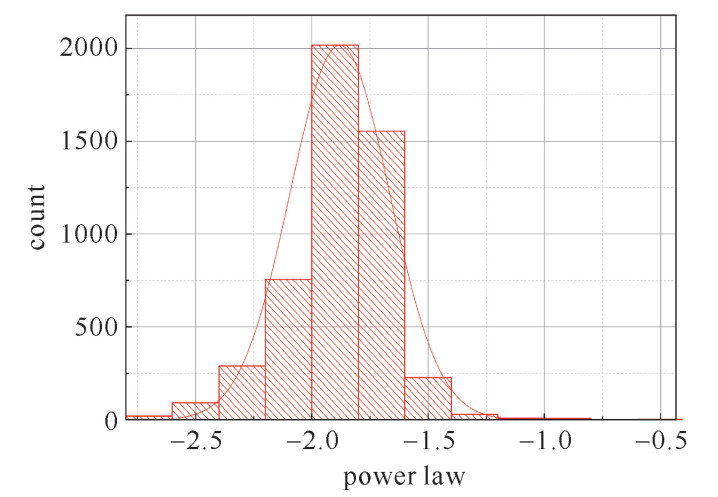
Re	Nu	h/(W·m^-2·K^-1)	M/ms	f_s/Hz	R/Ω	ρ₀/(Ω·mm²·m^-1)	d/μm
0.797	0.732	3 159.8	1.194	133.29	20	0.055	6

下载: 导出CSV

表 2 6 μm直径的钨丝不同幂率温度谱出现的概率

Table 2. Probability distributions of power law measurement with 6 μm tungsten wire

power law k	probability/%
>-5/3+0.20	1.6
-5/3-0.20~-5/3+0.20	52.2
-5/3-0.20	46.2

下载: 导出CSV

参考文献(16)

[1]	饶瑞中. 从光闪烁频谱反演大气湍流谱: 原理与数值模拟[J]. 力学学报, 2002, 34(5): 682. doi: 10.3321/j.issn:0459-1879.2002.05.004 Rao Ruizhong. Retrieval of turbulence spectrum from temporal spectrum of a light wave propagating through atmosphere: principle and simulations. Chinese Journal of Theoretical and Applied Mechanics, 2002, 34(5): 682 doi: 10.3321/j.issn:0459-1879.2002.05.004
[2]	Beland R R. Propagation through atmospheric optical turbulence[M]. Bellingham: SPIE Optical Engineering Press, 1993.
[3]	曾宗泳, 袁仁民, 谭锟, 等. 复杂地形近地面温度谱[J]. 量子电子学报, 1998, 4(2): 134-139. https://www.cnki.com.cn/Article/CJFDTOTAL-LDXU199802001.htm Zeng Zongyong, Yuan Renmin, Tan Kun, et al. The spectrum of temperature in the surface layer over complicated terrain. Chinese Journal of Quantum Electronics, 1998, 4(2): 134-139 https://www.cnki.com.cn/Article/CJFDTOTAL-LDXU199802001.htm
[4]	Jumper G Y, Vernin J, Azouit M, et al. Comparison of recent measurements of atmospheric optical turbulence[C]//36th Plasma Dynamics and Lasers Conference. 2005, AIAA-2005-4778.
[5]	Yao Yuancheng. Analysis of the influence factors to measurement of micro-thermometer. Hefei: University of Chinese Academy of Sciences, 2013: 68-72
[6]	Wyngaad J C, Izumi Y, Collins S A, et al. Behavior of the refractive-index-parameter near the ground[J]. J Opt Soc Am, 1971, 61: 1646-1650. doi: 10.1364/JOSA.61.001646
[7]	童诗白, 华成英. 模拟电路技术基础[M]. 北京: 高等教育出版社, 2006. Tong Shibai, Hua Chengying. The science of electroics: analog devices. Beijing: Higher Education Press, 2006
[8]	刘树棠, 朱茂林, 荣玫. 基于运算放大器和模拟集成电路的电路设计[M]. 西安: 西安交通大学出版社, 2014. Liu Shutang, Zhu Maolin, Rong Mei. Design with operational amplifiers and analog integrated circuits. Xi'an: Xi'an Jiaotong University Press, 2014
[9]	周秀骥, 陶善昌, 姚克亚. 高等大气物理学[M]. 北京: 气象出版社, 1991. 199-206. Zhou Xiuji, Tao Shanchang, Yao Keya. Advanced atmospheric physics. Beijing: China Meteorological Press, 1991. 199-206
[10]	塔塔尔斯基B N. 湍流大气中波的传播理论[M]. 温景嵩译. 北京: 科学出版社, 1978. Татарский В И. Theory of light propagation in turbulent atmosphere. Trans by Wen Jingsong. Beijing: Science Press, 1978
[11]	曾宗泳, 刘小勤, 马成胜, 等. 复杂地形近地面光学湍流[J]. 强激光与粒子束, 1999, 11(6): 668. http://www.hplpb.com.cn/article/id/1538 Zeng Zongyong, Liu Xiaoqin, Ma Chengsheng, et al. Optical turbulence in the surface layer over complex terrain. High Power Laser and Particle Beams, 1999, 11(6): 668 http://www.hplpb.com.cn/article/id/1538
[12]	梅海平, 吴晓庆, 饶瑞中. 非Kolmogorov大气湍流温度谱标度指数的测量与分析[J]. 强激光与粒子束, 2006, 18(9): 1423-1427. http://www.hplpb.com.cn/article/id/2740 Mei Haiping, Wu Xiaoqing, Rao Ruizhong, et al. Measurement and analysis of temperature power spectrum scaling exponent in non-Kolmogorov turbulent atmosphere. High Power Laser and Particle Beams, 2006, 18(9): 1423-1427 http://www.hplpb.com.cn/article/id/2740
[13]	吴晓庆, 王英俭, 曾宗泳, 等. 大气温度起伏谱的测量[J]. 强激光与粒子束, 2002, 14(2): 134-139. http://www.hplpb.com.cn/article/id/1238 Wu Xiaoqing, Wang Yingjian, Zeng Zongyong, et al. Measurement of the spectrum of atmospheric temperature fluctuations. High Power Laser and Particle Beams, 2002, 14(2): 134-139 http://www.hplpb.com.cn/article/id/1238
[14]	Pinton J F, Plaza F, Danaila L, et al. On velocity and passive scalar scaling laws in a turbulent swirling flow[J]. Physica D, 1998, 122: 187-201. doi: 10.1016/S0167-2789(98)00185-7
[15]	饶瑞中. 光在湍流大气中的传播[M]. 合肥: 安徽科学技术出版社, 2005: 76-77. Rao Ruizhong. Light propagation in the turbulent atmosphere. Hefei: Anhui Science and Technology Press, 2005: 76-77
[16]	饶瑞中, 李玉杰. 非Kolmogorov大气湍流中的光传播及其对光电工程的影响[J]. 光学学报, 2015, 35(5): 1-11. https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB201505003.htm Rao Ruizhong, Li Yujie. Light propagation through non-Kolmogorov-type atmospheric turbulence and its effects on optical engineering. Acta Optica Sinica, 2015, 35(5): 1-11 https://www.cnki.com.cn/Article/CJFDTOTAL-GXXB201505003.htm