Geodetic interface algorithm for evaluating geomagnetic storms in pipelines
-
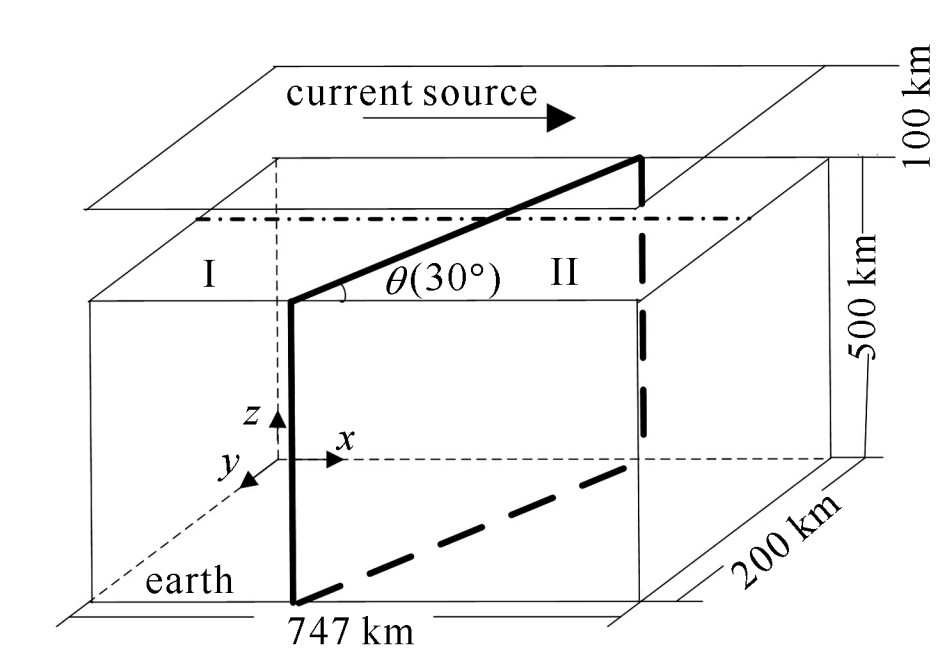
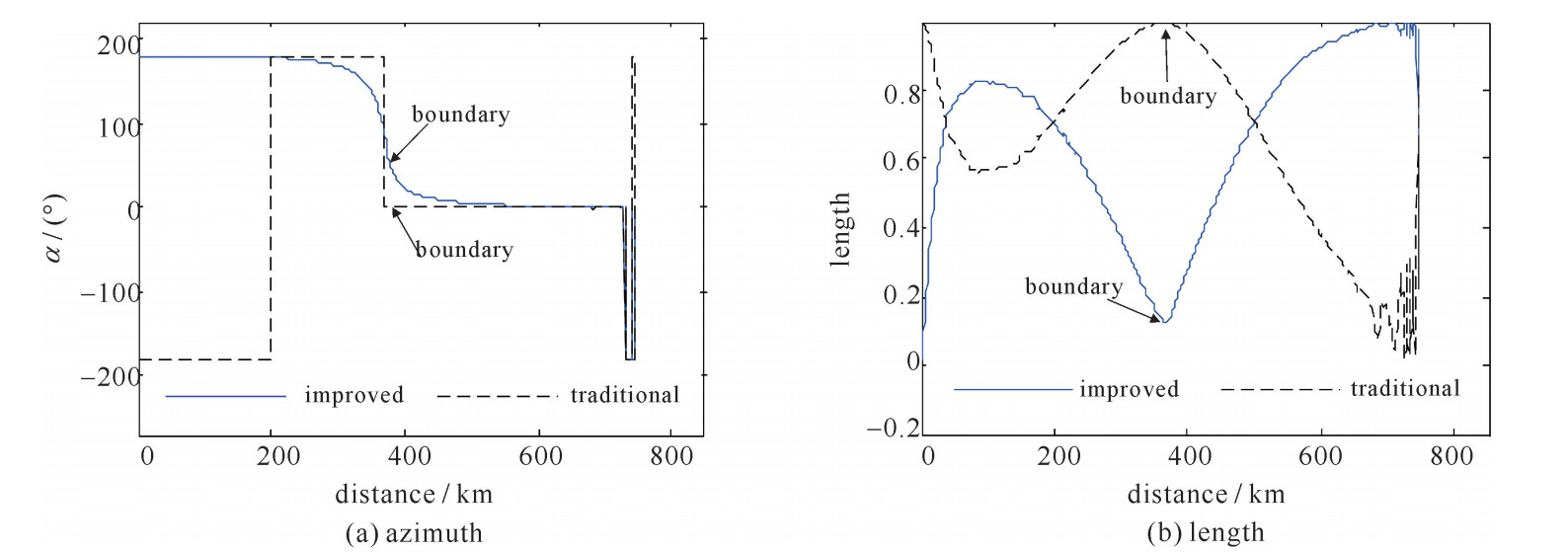
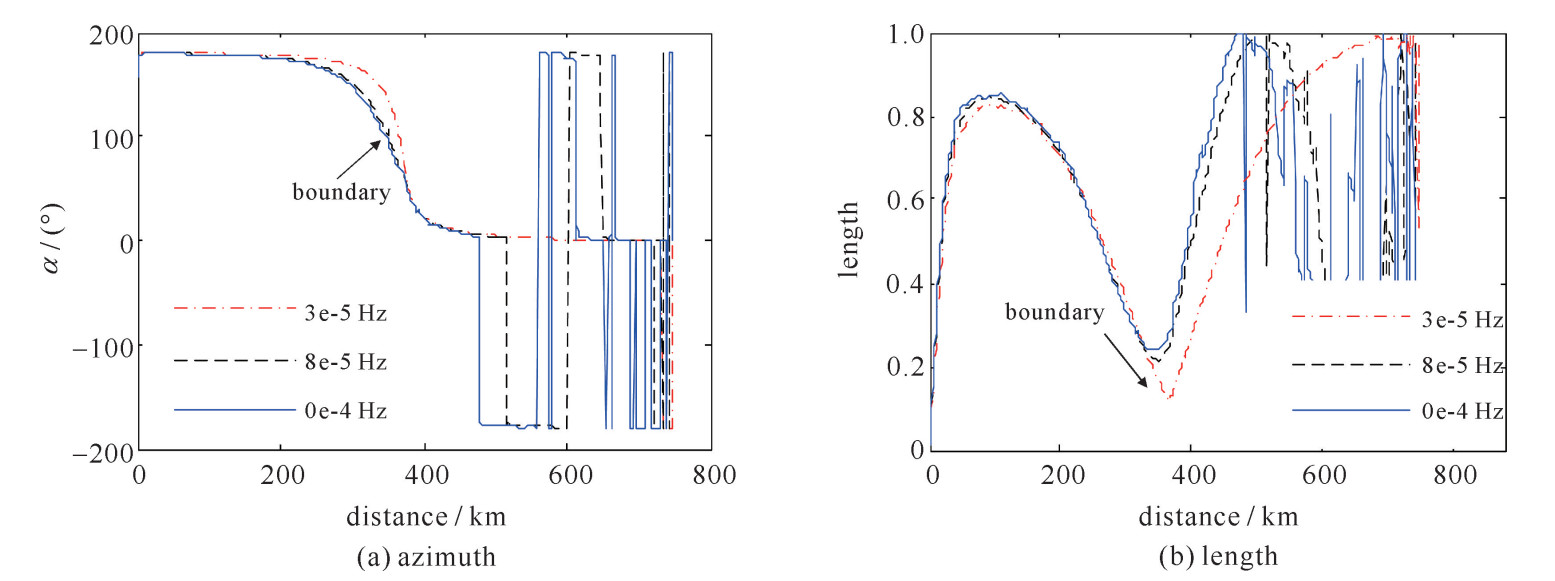
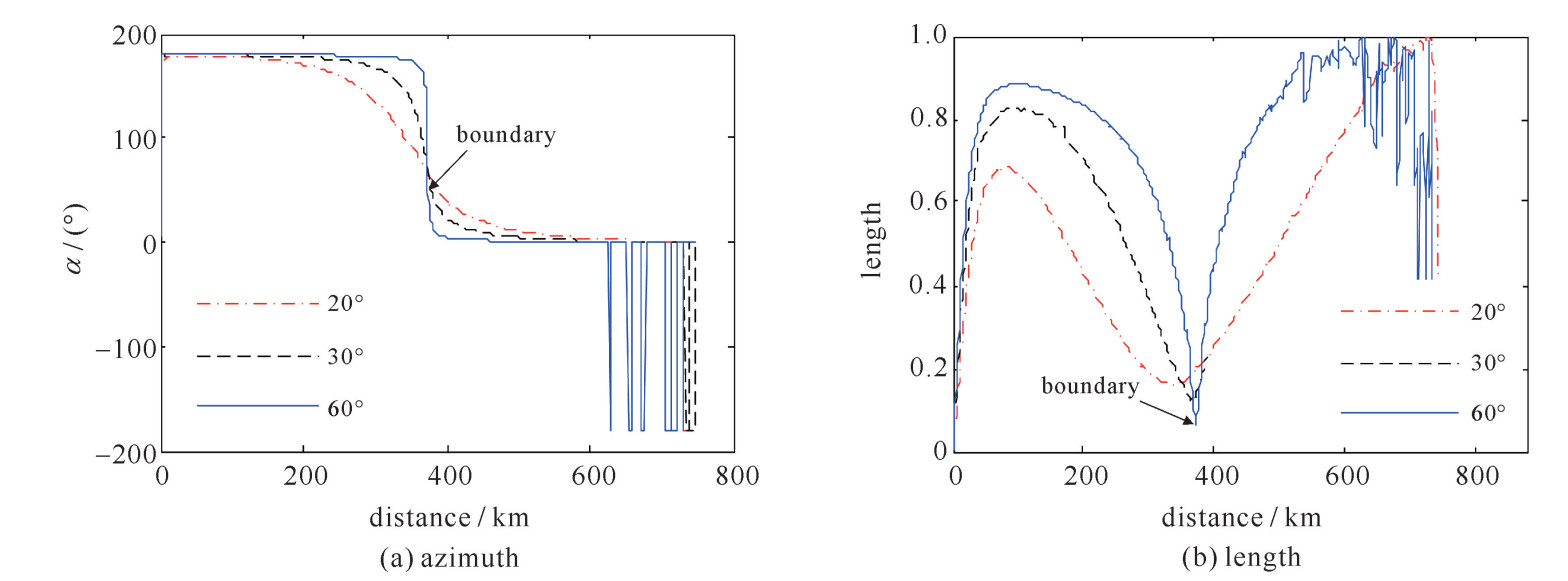
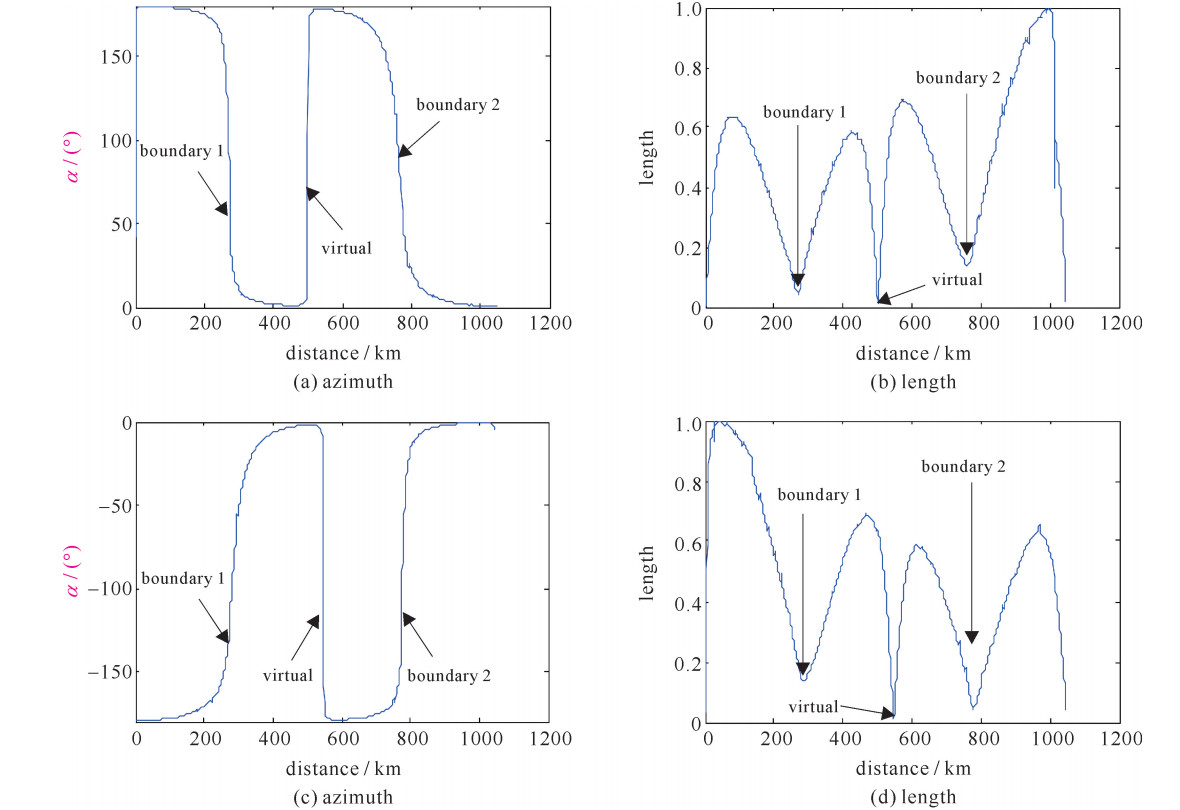
摘要: 大地电性结构的分界处容易加剧管道腐蚀, 穿过大地分界面的管道在分界点处受到的地磁暴致灾风险比较大, 提出一种可用于评估输油气管道的地磁暴灾害风险自评价描述的算法。改进算法的帕金森矢量在定位大地分界面时比传统算法的帕金森矢量更加准确; 在可以识别大地分界面的前提下, 改进算法的帕金森矢量方位角会在分界面附近完成±180°到0°或0°到±180°的过渡变化, 距离分界面越近, 方位角越能够反映大地分界面的倾向, 改进算法的帕金森矢量长度在分界点处达到最小值; 相邻地块电导率差值、空中电流源频率以及大地分界面与测线方向的夹角等因素会影响改进算法帕金森矢量的分布特性; 利用帕金森矢量的方位角图和长度图两个判据可以定位穿过分界面位置的管道, 相邻大地分界面之间存在虚拟界面, 需要分析排除。仿真结果表明了这些结论的正确性, 对管道防护具有重要的指导意义。Abstract: Pipeline corrosion is easily aggravated at the boundary of the earth's electrical structure.The pipeline passing through the earth interface is subject to greater risk of geomagnetic storm disaster at the demarcation point.The algorithm in this paper can be used to evaluate the self-evaluation description of geomagnetic storm disaster risk for oil and gas pipelines.This paper holds that the improved algorithm's Parkinson vector is more accurate than the traditional algorithm's Parkinson vector in locating the geodetic interface.On the premise that the earth's interface can be identified, the azimuth of the improved algorithm's Parkinson vector will change from ±180°to 0°or 0°to±180°near the interface, and the closer to the interface, the azimuth can better reflect the inclination of the earth interface, and the length reaches the minimum value at the boundary point.Factors such as conductivity difference between adjacent plots, the frequency of current sources and the angle between the earth's interface and the line direction will affect the distribution characteristics of the improved algorithm's Parkinson vector.The azimuth map and length map can be used to locate the pipeline through the interface position.There is a virtual interface between adjacent earth's interfaces, which needs analysis and exclusion.The simulation results show that these conclusions are correct and have important guiding significance for pipeline protection.
-
图 4 改进算法的帕金森矢量方位角和长度
Figure 4. Azimuth and length of improved algorithm's Parkinson vector
图 5 改进算法的帕金森矢量方位角和长度
Figure 5. Azimuth and length of improved algorithm's Parkinson vector
图 6 改进算法的帕金森矢量方位角和长度
Figure 6. Azimuth and length of improved algorithm's Parkinson vector
图 7 改进算法的帕金森矢量方位角和长度
Figure 7. Azimuth and length of improved algorithm's Parkinson vector
图 9 改进算法的帕金森矢量方位角和长度
Figure 9. Azimuth and length of improved algorithm's Parkinson vector
图 10 改进算法的帕金森矢量方位角和长度
Figure 10. Azimuth and length of improved algorithm's Parkinson vector
表 1 传统算法与改进算法的帕金森矢量不同点
Table 1. Difference between traditional algorithm's Parkinson vector and improved algorithm's Parkinson vector
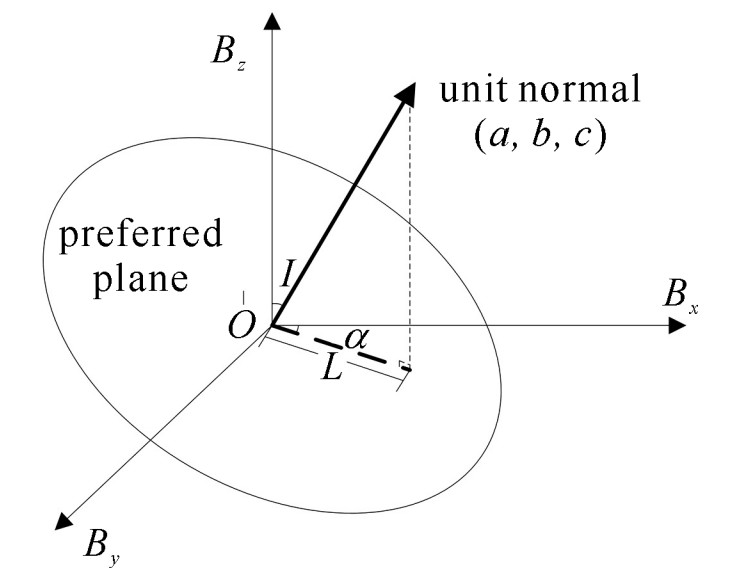
traditional algorithm’s Parkinson vector improved algorithm’s Parkinson vector preferred plane of geomagnetic variation vector aΔHi+b ΔDi+(-1) ΔZi=0[9] ΔF=a ΔBx+b ΔBy+c ΔBz geomagnetic difference vector the vector difference between the geomagnetic component at time t0 and t0+Δti(i=1, 2, …, n)[5-6] the vector difference between the geomagnetic component at time t0 and t0+1 steady state value no geomagnetic anomalies’s average value[11] the value at the previous moment Parkinson vector dip angle I=arctana ${\sqrt{a^2+b^2}}$[9] dip angle I=arctana $\sqrt{\frac{a^2+b^2}{c^2}}$ 
下载: 导出CSV
-
[1] 王琪. 浅谈输气管道安全运行必要性[J]. 化工管理, 2016(11): 9. https://www.cnki.com.cn/Article/CJFDTOTAL-FGGL201611006.htmWang Qi. Talking about the necessity of safe operation of gas transmission pipeline. Chemical Enterprise Management, 2016(11): 9 https://www.cnki.com.cn/Article/CJFDTOTAL-FGGL201611006.htm [2] Fernberg P A, Samson C, Boteler D H, et al. Earth conductivity structures and their effects on geomagnetic induction in pipelines[J]. Annales Geophysicae, 2007, 25(1): 207-208. doi: 10.5194/angeo-25-207-2007 [3] Shepherd S G, Shubitidze F, Lotko W. Calculating induced electric and magnetic fields near coastal regions[C]//EGS - AGU - EUG Joint Assembly. 2003. [4] 梁志珊. 一种埋地油气管道受地磁暴影响的GIC和PSP的计算方法: CN201510579331. X[P].Liang Zhishan. A calculation method of GIC and PSP for buried oil and gas pipeline affected by geomagnetic storm: CN201510579331. X [5] Parkinson W D. Directions of rapid geomagnetic fluctuations[J]. Geophysical Journal International, 1959, 2(1): 1-14. doi: 10.1111/j.1365-246X.1959.tb05776.x [6] Parkinson W D. The influence of continents and oceans on geomagnetic variations[J]. Geophysical Journal International, 2010, 6(4): 441-449. [7] Schmucker U. Anomalies of geomagnetic variations in the southwestern United States[J]. J Geomag Geoelectr, 1963, 15(4): 193-221. [8] 陈伯舫. 渤海西岸的电导率异常[J]. 地球物理学报, 1974(3): 169-172. https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX197403004.htmChen Bofang. Conductivity anomaly in west coast of Pohai. Acta Geophysica Sinica, 1974(3): 169-172 https://www.cnki.com.cn/Article/CJFDTOTAL-DQWX197403004.htm [9] 龚绍京, 刘双庆, 梁明剑. 中国大陆地磁帕金森矢量特征及其与主要构造关系[J]. 地震学报, 2017, 39(1): 47-63. https://www.cnki.com.cn/Article/CJFDTOTAL-DZXB201701005.htmGong Shaojing, Liu Shuangqing, Liang Mingjian. Characteristics of geomagnetic Parkinson vector in Chinese mainland and their tevtonic implication. Acta Seismologica Sinica, 2017, 39(1): 47-63 https://www.cnki.com.cn/Article/CJFDTOTAL-DZXB201701005.htm [10] Baecher G B, Lanney N A, Einstein H H. Statistical description of rock properties and sampling[C]//The 18th US Symposium on Rock Mechanics(USRMS). 1977: 1-8. [11] 龚绍京. 广东省地磁台的帕金森矢量及广州台的系数在河源地震前后的时间变化[J]. 地震研究, 1987(5): 575-582. https://www.cnki.com.cn/Article/CJFDTOTAL-DZYJ198705006.htmGong Shaojing. Parkinson vector at the geomagnetic stations in Guangdong province and the time-dependent changes of their ratio at Guangzhou station both before and after the Heyuan earthquake. Journal of Seismological Research, 1987(5): 575-582 https://www.cnki.com.cn/Article/CJFDTOTAL-DZYJ198705006.htm [12] 中国地震局. 地震及前兆数字观测技术规范-地震观测: 试行[M]. 北京: 地震出版社, 2001.China Earthquake Administration. Earthquake and precursor digital observation technical specifications-Earthquake observation: Trial. Beijing: Seismological Press, 2001 -
点击查看大图
计量
- 文章访问数: 1322
- HTML全文浏览量: 379
- PDF下载量: 63
- 被引次数: 0
