Target recognition method for radio fuze based on KFCM algorithm with incremental update
-
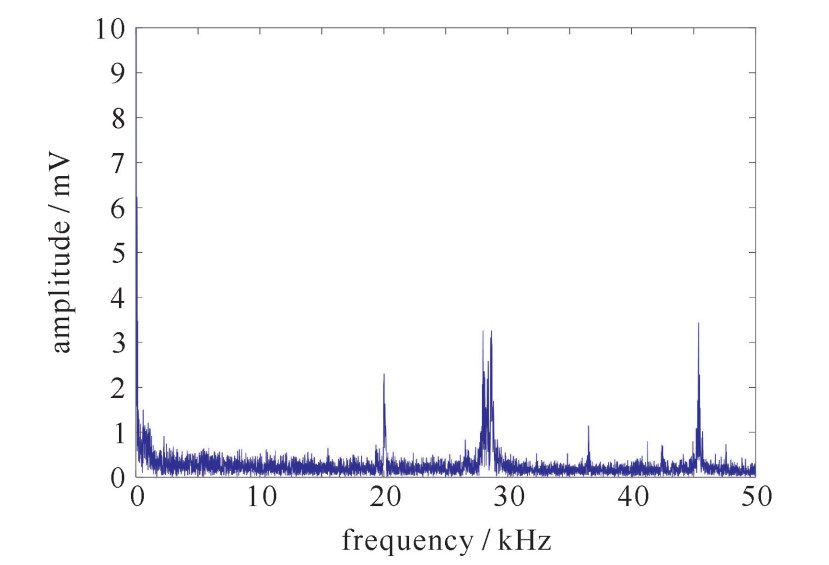
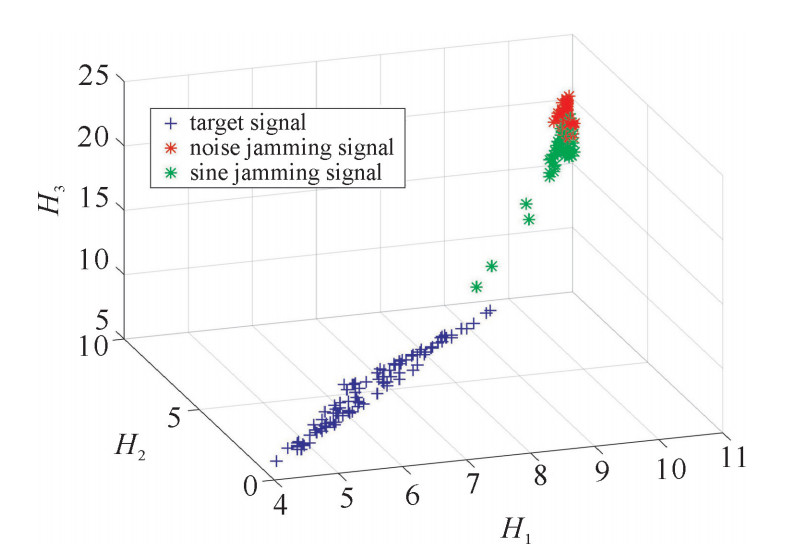
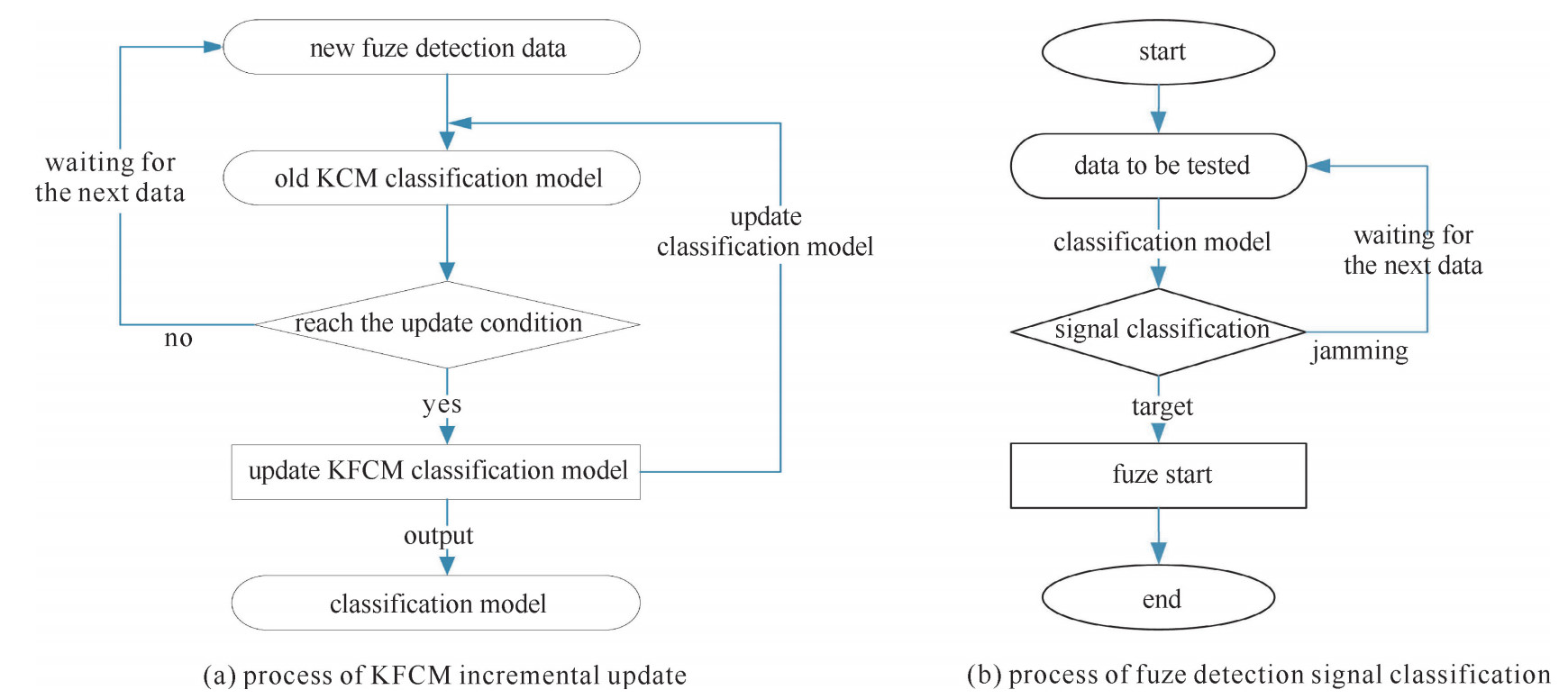
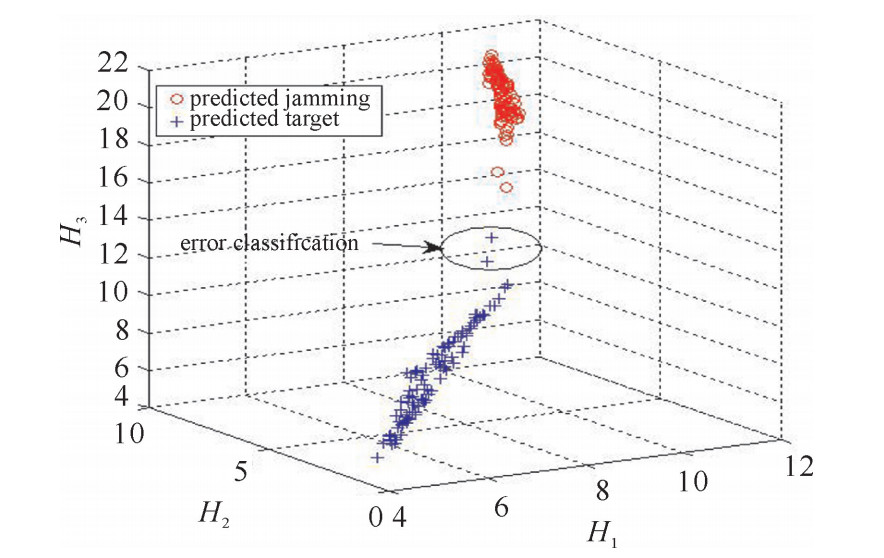
摘要: 针对传统无线电引信在复杂电磁环境下作用效果较差的问题，以连续波多普勒引信为例，通过对引信检波输出信号频域的分析，提出一种基于熵的特征提取方法，并利用KFCM算法对信号进行分类识别。由于实际战场环境复杂且不可预测，其背景噪声强度与实验环境下存在差异，因此结合KFCM增量更新特性，使分类模型根据噪声强度变化而实时更新调整，从而达到更好的分类效果。实验结果证明，基于增量更新KFCM算法能显著提高不同信噪比下引信目标识别能力，将KFCM增量更新算法运用到无线电引信抗干扰能取得良好效果。Abstract: The complex electromagnetic environment is a great threat to radio fuze, taking continuous wave Doppler radio fuze for example, a method based on frequency entropy by analyzing the frequency domain characteristic fuze detection output signal is proposed. The KFCM algorithm is used for classifying and recognizing target signal and jamming signal. As the end trajectory characteristic of fuze determines the fact that the received jamming signal power increase rapidly and the signal-to-noise ratio gets worse. Thus, combined with the KFCM incremental update model, the classification model is adjusted in real time according to signal-to-noise ratio to get a better effect. The result of experiment indicate that the KFCM algorithm with incremental update has good effect on the classification and recognition of target signal at different signal-to-noise ratio, and it can effectively improve the ability of anti-jamming of radio fuze.
-
图 1 实测目标作用下引信检波输出频谱
Figure 1. Actually measured Fourier spectrum of fuze detection signal under the action of target signal
图 2 实测噪声调幅扫频干扰下引信检波输出结果
Figure 2. Actually measured Fourier spectrum of fuze detection signal under the action of noise amplitude modulation frequency sweeping jamming signal
图 3 引信检波信号频域熵3维分布
Figure 3. Three-dimension distribution of frequency entropy of fuze detection signal
图 4 基于KFCM增量更新的引信检波分类流程
Figure 4. Process of fuze detection signal classification based on KFCM incremental update
图 5 基于KFCM的引信检波信号分类结果
Figure 5. Classification result of fuze detection signal based on KFCM
图 6 更新后的KFCM分类模型在不同信噪比下目标识别率
Figure 6. Target recognition accuracy of KFCM model after update at different signal-to-noise ratio
图 7 不同更新次数下引信目标识别正确率
Figure 7. Classification accuracy of fuze detection signal at different update times
表 1 KFCM算法改进前后实验结果
Table 1. Result before and after the improvement of KFCM
average accuracy/% test times original 94.7 200 improved 98.9 200 
下载: 导出CSV
表 2 基于KFCM的引信目标信号识别结果
Table 2. Results of fuze target signal recognition based on KFCM
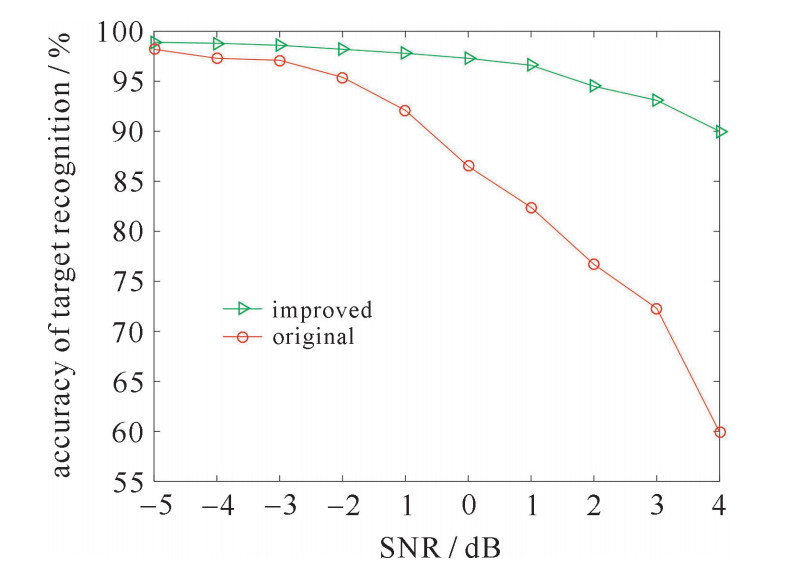
SNR/ dB average accuracy/% test times 5 99.02 200
下载: 导出CSV
表 3 不同更新次数下引信目标识别正确率
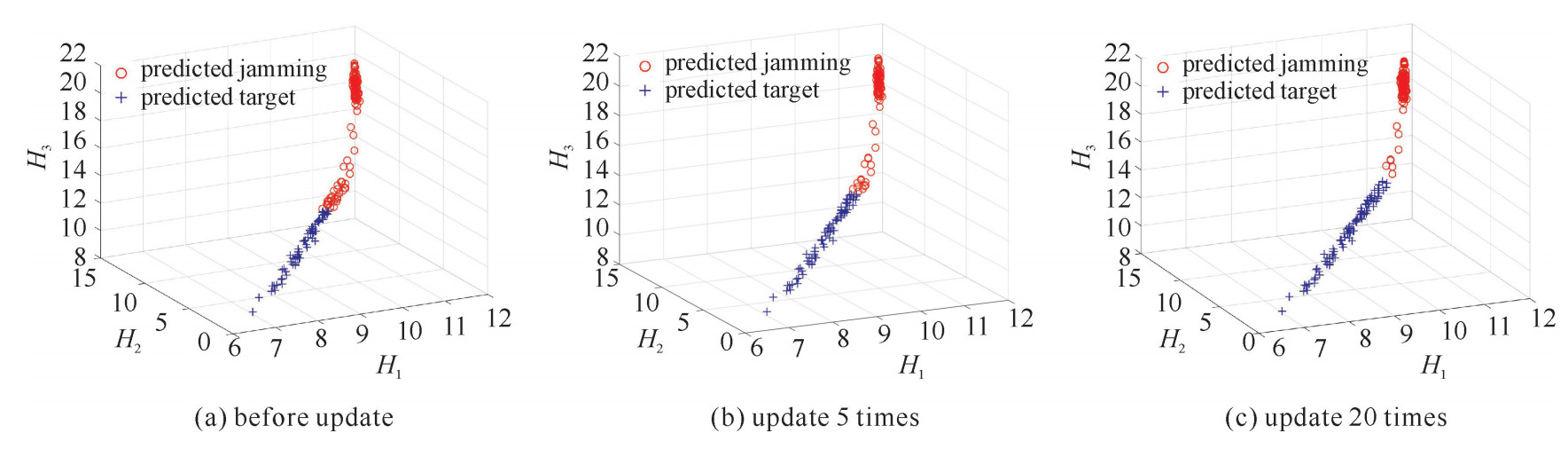
Table 3. Classification accuracy at different update times
incremental update times average accuracy/% test times 0(original) 81.46 200 5 91.55 200 20 97.23 200
下载: 导出CSV
-
[1] 崔占忠, 宋世和, 徐立新. 近炸引信原理[M]. 3版. 北京: 北京理工大学出版社, 2009: 15-43.Cui Zhanzhong, Song Shihe, Xu Lixin. Principle of proximity fuze. 3rd ed. Beijing: Beijing Institute of Technology Press, 2009: 15-43 [2] 赵惠昌. 无线电引信设计原理与方法[M]. 北京: 国防工业出版社, 2012.Zhao Huichang. Principle and method of radio fuze design. Beijing: National Defense Industry Press, 2012: 34-75 [3] 李志强. 连续波多普勒无线电引信目标信号识别方法研究[D]. 北京: 北京理工大学, 2014: 7-28.Li Zhiqiang. On recognition of target signal for CW Doppler radio proximity fuze. Beijing: Beijing Institute of Techonolgy, 2014: 7-28 [4] 郭云鹏, 闫晓鹏, 李泽, 等. 基于处理增益的连续波多普勒引信干扰效能分析方法[J]. 探测与控制学报, 2017, 39(5): 20-25, 30.Guo Yunpeng, Yan Xiaopeng, Li Ze, et al. Analysis of CW Doppler fuze jamming performance based on processing gain. Journal of Detection and Control, 2017, 39(5): 20-30 [5] 单剑锋, 翟波. 基于小波变换的无线电引信目标识别研究[J]. 弹箭与制导学报, 2009, 29(6): 288-290. doi: 10.3969/j.issn.1673-9728.2009.06.080Shan Jianfeng, Zhai Bo. Wavelet based target detection for radio fuze signal. Journal of Projectiles, Rockets, Missiles and Guidance, 2009, 29(6): 288-290 doi: 10.3969/j.issn.1673-9728.2009.06.080 [6] 张彪, 闫晓鹏, 栗苹, 等. 基于支持向量机的无线电引信抗扫频式干扰研究[J]. 兵工学报, 2016, 37(4): 635-640. doi: 10.3969/j.issn.1000-1093.2016.04.009Zhang Biao, Yan Xiaopeng, Li Ping, et al. Research on anti-frequency sweeping jamming of radio fuze based on support vector machine. Acta Armamentarii, 2016, 37(4): 635-640 doi: 10.3969/j.issn.1000-1093.2016.04.009 [7] 卢云龙, 李明, 陈洪猛, 等. 基于熵特征的DRFM有源欺骗干扰CFAR检测[J]. 系统工程与电子技术, 2016, 38(4): 732-738. https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201604003.htmLu Yunlong, Li Ming, Chen Hongmeng, et al. CFAR detection of DRFM deception jamming based on entropy feature. Systems Engineering and Electronics, 2016, 38(4): 732-738 https://www.cnki.com.cn/Article/CJFDTOTAL-XTYD201604003.htm [8] Zhen J D. Pan H Y. Cheng J S. Rolling bearing fault detection and diagnosis based on composite multiscale fuzzy entropy and ensemble support vector machines[J]. Mechanical Systems And Signal Processing, 2016, 85(10): 746-759. [9] 钟珞, 潘昊, 封筠, 等. 模式识别[M]. 武汉: 武汉大学出版社, 2006: 53-86.Zhong Luo, Pan Hao, Feng Yun, et al. Pattern recognition[M]. Wuhan: Wuhan University Press, 2006: 53-86 [10] Zhang D Q, Chen S C. Clustering incomplete data using kernel-based fuzzy c-means algorithm[J]. Neural Processing Letters, 2003, 18(3): 155-162. doi: 10.1023/B:NEPL.0000011135.19145.1b [11] Lin K P. A novel evolutionary kernel intuitionistic fuzzy C-means clustering algorithm[J]. IEEE Trans Fuzzy Systems, 2014, 22(5): 1074-1087. doi: 10.1109/TFUZZ.2013.2280141 [12] 吴佳. FCM聚类及其增量算法的研究[D]. 长沙: 长沙理工大学, 2011: 12-39.Wu Jia. FCM clustering and research of its increment algorithm. Changsha: Changsha University of Science & Technology, 2011: 12-39 -
点击查看大图
计量
- 文章访问数: 1130
- HTML全文浏览量: 312
- PDF下载量: 77
- 被引次数: 0
