Transient response of overhead and buried multiconductor lines to HEMP
-
摘要: 针对瞬态电磁场辐照多导体电缆问题，首先介绍了一种用于计算架空及埋地线缆瞬态响应的高效时域宏模型。该模型基于传输线理论，利用广义特征线法和SPICE求解器中集成的模拟行为建模库，在时域内实现建模过程中涉及的频率相关参数和卷积计算。该方法适用性广泛，可同时用于架空及埋地线缆的场线耦合建模仿真；与现有时域有限差分法相比，不需要对时间和空间进行离散，以及对频率相关参数进行矢量匹配或数值逆傅里叶变换，因此可简化建模步骤，提高建模及仿真计算的效率；该宏模型计算效率不受线缆长度限制，适用于研究多导体长距离线缆。其次，在时域和频域分别研究了高空电磁脉冲(HEMP)的环境及特点。最后，利用算例验证了所提宏模型计算架空及埋地线缆响应的有效性，并利用该方法分别研究了架空地线对三相输电线路瞬态响应的影响以及埋地电力电缆金属护套在端接线性及非线性保护器件时对HEMP的瞬态响应。结果表明，宏模型法可在时域内高效地计算入射场耦合架空输电线及埋地电力电缆的瞬态响应，特别是对于带有非线性器件的长多导体线缆。Abstract: This paper presents an efficient time-domain macromodeling algorithm to calculate current and voltage responses of overhead and buried lines to incident field coupling. Based on transmission line theory, the proposed macromodel adopts the analog behavioral modeling of Spice solvers and generalized Method of Characteristics (MoC) to model the frequency-dependent variables, and to calculate the convolution in time domain. This method has a wide applicability as it can both model field coupling to overhead and buried lines. Compared with the finite different time domain method, there is no need to discretize time and space, and adopt numerical inverse Fourier transform or vector fitting method to obtain transient parameters. The efficiency of the macromodel is not limited by line length, so it is valid for modeling long multiconductor lines. Furthermore, the environment and characteristics of HEMP are studied in time and frequency domain, respectively. Finally, two examples are studied to validate the proposed method for field coupling to overhead and buried lines. Using this method, effects of overhead grounding lines on transient response of three-phase power lines and buried power cables terminated with linear or nonlinear protective loads are investigated, respectively. All results show that the macromodel can efficiently calculate the transient responses of incident field coupling to overhead and buried power lines in time domain, especially for long multiconductors with nonlinear elements.
-
图 1 外场辐照架空和埋地多导体线缆示意图
Figure 1. Geometric configuration for external field coupling to overhead and buried transmission lines
图 3 不同土壤电导率和深度处透射电场时域波形
Figure 3. Time-domain waveform of transmitted electric field for different ground conductivities and depths
图 4 不同土壤电导率对应的透射电场幅度谱和归一化累积能流谱
Figure 4. Amplitude frequency spectrum and cumulative amount of energy fluence of transmitted electric field for different ground conductivities
图 5 不同距地面深度对应透射电场的幅度谱和归一化累积能流谱
Figure 5. Amplitude frequency spectrum and cumulative amount of energy fluence of transmitted electric field for different depths
图 6 外场辐照架空线示意图
Figure 6. Geometry of transient plane wave coupling to overhead transmission lines
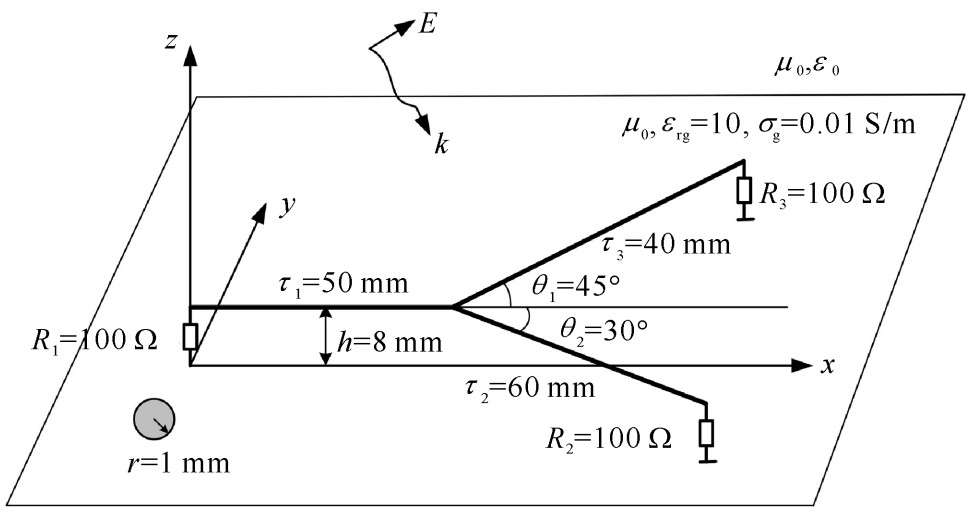
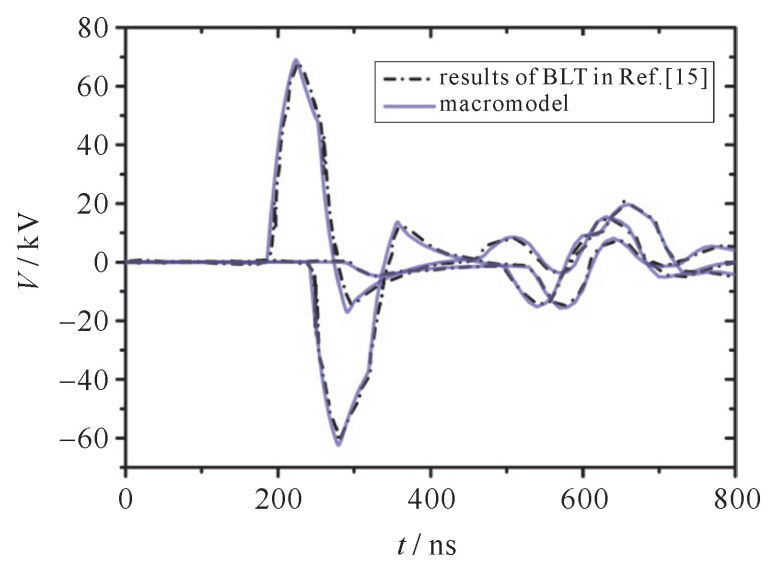
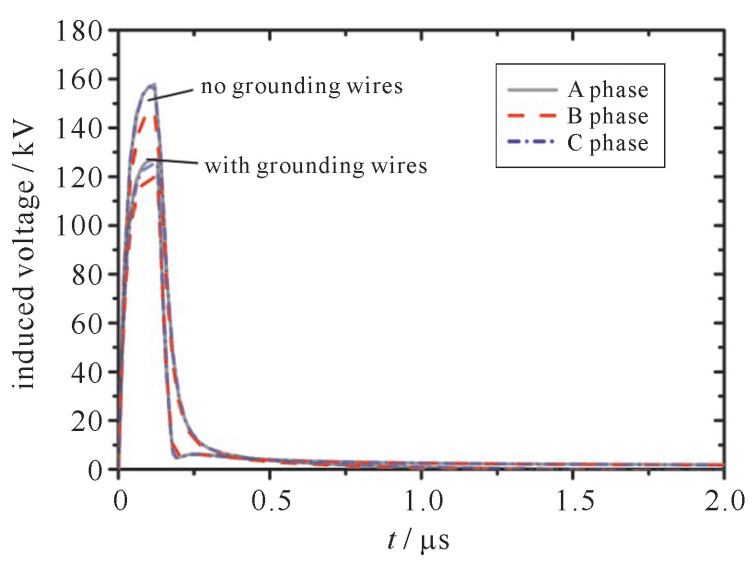
图 7 负载R1，R2和R3上感应电压比较
Figure 7. Comparing results of induced voltages at the terminal ends obtained via macromodel and BLT in Ref[15]
图 9 外场辐照750 kV三相单回交流输电线路示意图
Figure 9. Geometry of plane wave coupling to 750 kV three-phase single-back overhead power lines
图 12 外场辐照端接接地电阻的单根埋地绝缘电缆示意图
Figure 12. Geometry of transient plane wave coupling to a buried insulated cable loaded with grounding resistances
图 13 不同土壤电导率对应的电缆末端瞬态感应电流比较
Figure 13. Comparison of transient induced currents at the far terminal grounding resistive for different ground conductivity
图 14 三相埋地单芯电缆一端互联经护层过电压保护器接地示意图
Figure 14. Configuration of three-phase buried cables connected with sheath protector
-
[1] Petrache E, Rachidi F, Paolone M, et al. Lightning induced disturbances in buried cables—Part I: Theory[J]. IEEE Trans Electromagnetic Compatibility, 2005, 47(3): 498-508. doi: 10.1109/TEMC.2005.853161 [2] Theethayi N, Thottappillil R, Paolone M, et al. External impedance and admittance of buried horizontal wires for transient studies using transmission line analysis[J]. IEEE Trans Dielectrics & Electrical Insulation, 2007, 14(3): 751-761. [3] 王川川, 朱长青, 周星, 等. 有限长度埋地多导体电缆对外界电磁场响应特性分析[J]. 高电压技术, 2012, 38(11): 2836-2842. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201211009.htmWang Chuanchuan, Zhu Changqing, Zhou Xing, et al. Response analysis on buried multiconductor cable with finite length to external electromagnetic field. High Voltage Engineering, 2012, 38(11): 2836-2842 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201211009.htm [4] 周星, 王川川, 朱长青, 等. 外场辐照下埋地电缆瞬态响应规律研究[J]. 高压电器, 2013(12): 7-12. https://www.cnki.com.cn/Article/CJFDTOTAL-GYDQ201312002.htmZhou Xing, Wang Chuanchuan, Zhu Changqing, et al. Transient induction response law of buried cable excited by external electromagnetic field. High Voltage Apparatus, 2013, 49(12): 7-12 https://www.cnki.com.cn/Article/CJFDTOTAL-GYDQ201312002.htm [5] Xu F, Liu C, Hong W, et al. Fast and accurate transient analysis of buried wires and its applications[J]. IEEE Trans Electromagnetic Compatibility, 2014, 56(1): 188-199. doi: 10.1109/TEMC.2013.2272041 [6] 孙蓓云, 崔志同, 周辉, 等. 埋地电缆高空电磁脉冲耦合响应[J]. 现代应用物理, 2014, 5(4): 269-274. doi: 10.3969/j.issn.2095-6223.2014.04.004Sun Beiyun, Cui Zhitong, Zhou Hui, et al. Coupling effects of HEMP on buried cables. Modern Applied Physics, 2014, 5(4): 269-274 doi: 10.3969/j.issn.2095-6223.2014.04.004 [7] 刘青, 谢彦召. 高空电磁脉冲作用下埋地电缆的瞬态响应规律[J]. 高电压技术, 2017, 43(9): 3014-3020. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201709032.htmLiu Qing, Xie Yanzhao. Transient response law of buried cable to high-altitude electromagnetic pulse. High Voltage Engineering, 2017, 43(9): 3014-3020 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ201709032.htm [8] Guo J, Xie Y, Qiu A. Calculation of lightning induced voltages on overhead lines using an analytical fitting representation of electric fields[J]. IEEE Trans Electromagnetic Compatibility, 2016: 1-8. [9] Liu X, Cui X, Qi L. Calculation of lightning-induced overvoltages on overhead lines based on DEPACT macromodel using circuit simulation software[J]. IEEE Trans Electromagnetic Compatibility, 2012, 54(4): 837-849. doi: 10.1109/TEMC.2011.2175230 [10] Paul C R. Analysis of multiconductor transmission lines[M]. NewYork: Wiley, 1994. [11] Du Z, Xie Y Z, Canavero F G. A Spice-compatible macromodel for field coupling to multiconductor transmission lines based on the analog behavioral modeling[J]. IEEE Trans Electromagnetic Compatibility, 2018: 1-7. [12] Papadopoulos T A, Tsiamitros D A, Papagiannis G K. Impedances and admittances of underground cables for the homogeneous earth case[J]. IEEE Trans Power Delivery, 2010, 25(2): 961-969. [13] Papagiannis G K, Tsiamitros D A, Labridis D P, et al. Direct numerical evaluation of earth return path impedances of underground cables[J]. IEE Proceedings-Generation, Transmission and Distribution, 2005, 152(3): 321. [14] 谢彦召, 王赞基, 王群书, 等. 高空核爆电磁脉冲波形标准及特征分析[J]. 强激光与粒子束, 2003, 15(8): 781-787. http://www.hplpb.com.cn/article/id/30Xie Yanzhao, Wang Zanji, Wang Qunshu, et al. High altitude nuclear electromagnetic pulse waveform standards: a review. High Power Laser and Particle Beams, 2003, 15(8): 781-787 http://www.hplpb.com.cn/article/id/30 [15] Xie H, Yong L, Qiao H, et al. Empirical formula of effective coupling length for transmission lines illuminated by E1 HEMP[J]. IEEE Trans Electromagnetic Compatibility, 2016, 58(2): 581-587. [16] Tesche F M, Ianoz M V, Karlsson T. EMC analysis methods and computational models[M]. NewYork: Wiley, 1997. [17] DL/T401-2002, 高压电缆选用导则[S].DL/T401-2002, Guide to the selection of high-voltage cables -
下载:
点击查看大图
计量
- 文章访问数: 1084
- HTML全文浏览量: 419
- PDF下载量: 130
- 被引次数: 0
