地磁暴条件下电网连锁故障风险评估

康小宁; 张亚刚; 徐旖旎; 郭明达; 张欣悦

doi:10.11884/HPLPB201931.190171

地磁暴条件下电网连锁故障风险评估

doi: 10.11884/HPLPB201931.190171

西安交通大学陕西省智能电网重点实验室, 西安 710049

基金项目:

国家重点研发计划项目 2016YFC0800100

详细信息

作者简介:
康小宁(1968—), 男, 教授, 从事电力系统继电保护与变电站综合自动化系统研究, kangxn@xjtu.edu.cn

通讯作者:
张亚刚(1995—), 男, 硕士研究生, 从事重大灾害下电力系统风险评估研究, zhang_yagang@163.com

中图分类号: TM732
计量
- 文章访问数: 2173
- HTML全文浏览量: 606
- PDF下载量: 100
- 被引次数: 0
出版历程
- 收稿日期: 2019-05-17
- 修回日期: 2019-06-15
- 刊出日期: 2019-07-15

Power system fault chain simulation model considering effect of geomagnetic storm conditions

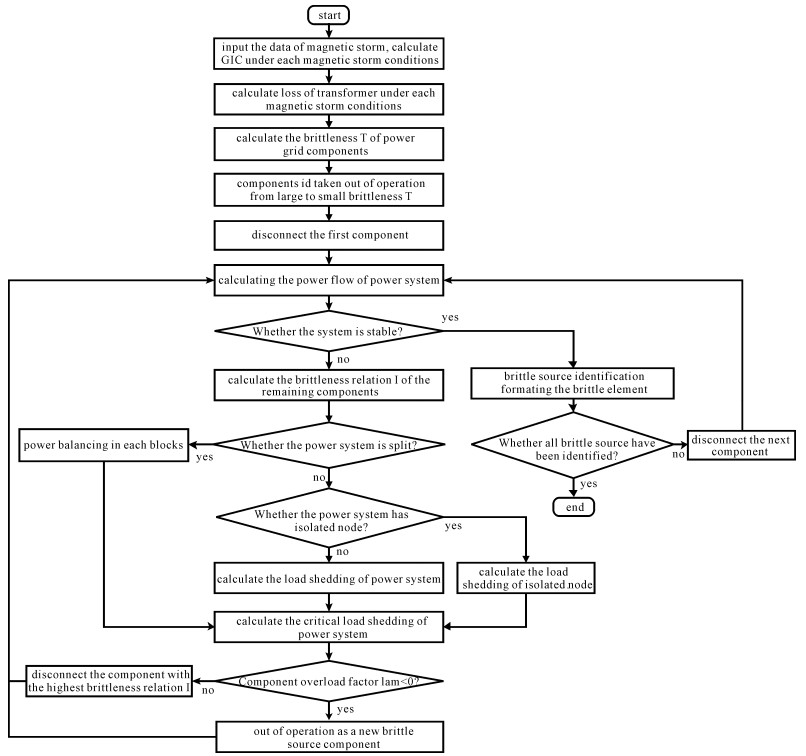
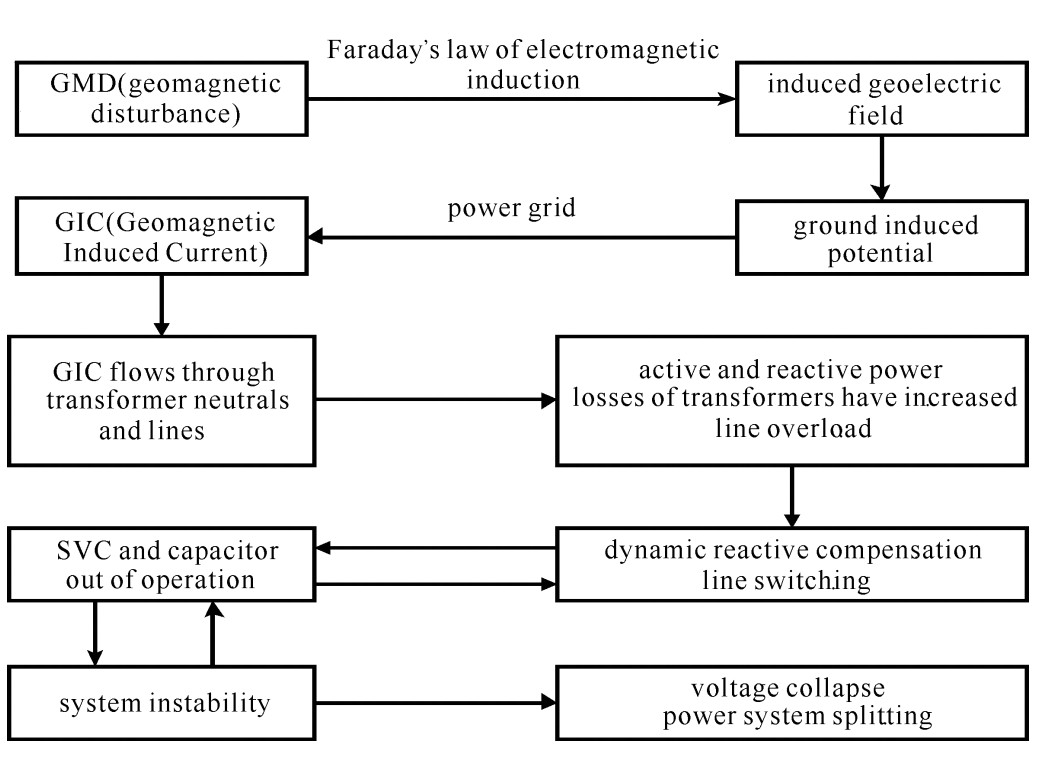
Shaanxi Key Laboratory of Smart Grid, Xi'an Jiaotong University, Xi'an 710049, China

摘要

摘要: 地磁扰动会在高压电网中诱发产生地磁感应电流(GIC), 使得电力变压器等发生相继故障, 从而导致电力系统崩溃或者引起大停电事故, 研究地磁暴条件下电网连锁故障风险评估能够为预防其引起的电网事故提供重要参考。对地磁暴条件下电网连锁故障的机理进行了分析, 提出了地磁暴条件下电网连锁故障风险评估流程, 该流程可以识别各个地磁暴条件下电网的薄弱环节; 利用系统的负荷削减量来评估连锁故障各个阶段对系统的危害, 同时利用给定地磁暴条件下该薄弱环节导致电力系统崩溃所削减的临界负荷量来评估其对电力系统的危害。利用IEEE-RTS79系统对于所提出的流程进行验证, 验证结果表明所提出流程的可行性和有效性, 所得结果可以为量化和防范地磁暴电网风险提供参考。
- 地磁暴 /
- 地磁感应电流 /
- 连锁故障 /
- 风险评估 /
- 负荷削减 /
- 脆性理论
Abstract: Geomagnetic disturbances will induce Geomagnetically Induced Current (GIC) in high voltage power grid, which will cause cascading failure in power grid, resulting in power system collapse or blackout.Therefore, research on risk assessment of cascading failure in power grid under geomagnetic storms can provide important reference for preventing accidents caused by geomagnetic storms.This paper analyzes the mechanism of cascading failure under geomagnetic storm conditions and proposes a risk assessment process for cascading failure in power grid under geomagnetic storms.The process can identify the vulnerable links of the power grid under each geomagnetic storm condition, evaluate the risk of the different stages of the vulnerable links by using the load shedding of the power system and use the critical load shedding caused by vulnerable links to evaluate its risk to the power system.Finally, the proposed process is verified by using the IEEE-RTS79 system.The verification results show the feasibility and validity of the proposed process.The results obtained can provide a reference for quantifying and preventing the risk of the power grid under geomagnetic storm conditions.
- geomagnetic storm /
- geomagnetically induced current /
- cascading failure /
- risk assess ment /
- load shedding /
- brittleness theory

HTML全文

图 1 地磁暴灾害下电网电压崩溃过程

Figure 1. Process of voltage collapse under geomagnetic storms

下载: 全尺寸图片幻灯片

图 2 地磁暴条件下电网连锁故障风险评估流程

Figure 2. Risk assessment process for cascading failures of power grids under geomagnetic storms

下载: 全尺寸图片幻灯片

图 3 GIC计算模型

Figure 3. Computing model of GIC

下载: 全尺寸图片幻灯片

图 4 脆性基元

Figure 4. Brittle elements

下载: 全尺寸图片幻灯片

图 5 IEEE-RTS79系统拓扑图

Figure 5. Topology of IEEE-RTS79

下载: 全尺寸图片幻灯片

表 1 各个地磁暴条件下电力系统的薄弱环节

Table 1. Vulnerable links of power system under each geomagnetic storm level

No.	E=0 (V/km)	$E=3 \sqrt{2} \angle 45^{\circ}(\mathrm{V} / \mathrm{km})$	$E=5 \sqrt{2} \angle 45^{\circ}(\mathrm{V} / \mathrm{km})$	$E=9 \sqrt{2} \angle 45^{\circ}(\mathrm{V} / \mathrm{km})$
1	L11	L11	L11	L11
2	L10	L10	L10	L19
3	L7(T)-L29-L23	L7(T)-L29-L23	L27	L10
4	L27-L29-L23	L27	L23-L19	L18
5	L23-L18-L20-L21-L7-L11	L3-L28-L24-L29-L18-L20-L21	L7(T)-L29-L23	L2
6	L5-L11	L23-L18-L20-L21-L7-L11	L4-L11	L12
7	L17(T)-L16(T)-L3-L12-L5	L17(T)-L16(T)-L3-L5-L12	L18-L23-L19	L20

下载: 导出CSV

表 2 连锁故障评估

Table 2. Assessment of cascading failure

No.	branch	Δ P/MW	(Δ P/P_D)/%
1	L23	13.61	0.48
2	L18	195.49	6.86
3	L20	166.27	5.83
4	L21	238.19	8.36
5	L7(T)	228.40	8.10
6	L11	—	—
Δ P_S	—	841.96	29.63

下载: 导出CSV

表 3 $E=3 \sqrt{2} \angle 45^{\circ}$条件下各个故障链的临界负荷削减量

Table 3. Critical load shedding of vulnerable links under $E=3 \sqrt{2} \angle 45^{\circ}$

No.	$E=3 \sqrt{2} \angle 45^{\circ}$ (V/km)	Δ P_S/MW	(Δ P_S/ P_D)/%
1	L11	—	—
2	L10	—	—
3	L7(T)-L29-L23	76.16	2.67
4	L27	—	—
5	L3-L28-L24-L29-L18-L20-L21	383.49	13.46
6	L23-L18-L20-L21-L7(T)-L11	841.96	29.63
7	L17(T)-L16(T)-L3-L5-L12	288.13	10.11

下载: 导出CSV

参考文献(20)

[1]	Boteler D H, Pirjola R J, Nevanlinna H. The effects of geomagnetic disturbances on electrical systems at the Earth's surface[J]. Advances in Space Research, 1988, 22(1): 17-27.
[2]	刘连光, 吴伟丽. 磁暴影响电力系统安全风险评估思路与理论框架[J]. 中国电机工程学报, 2014, 34(10): 1583-1591. doi: 10.13334/j.0258-8013.pcsee.2014.10.009 Liu Lianguang, Wu Weili. Security risk assessment ideas and theoretical framework for power system considering geomagnetic storm. Proceedings of the CSEE, 2014, 34(10): 1583-1591 doi: 10.13334/j.0258-8013.pcsee.2014.10.009
[3]	Kappaenman J G, Albertson V D. Bracing for the geomagnetic storms[J]. IEEE Spectrum, 1990, 27(3): 27-33. doi: 10.1109/6.48847
[4]	刘连光, 刘春明, 张冰, 等. 中国广东电网的几次强磁暴影响事件[J]. 地球物理学报, 2008, 51(4): 976-981. doi: 10.3321/j.issn:0001-5733.2008.04.004 Liu Lianguang, Liu Chunming, Zhang Bing, et al. Strong magnetic storm's influence on China's Guangdong power grid. Chinese Journal of Geophysics, 2008, 51(4): 976-981 doi: 10.3321/j.issn:0001-5733.2008.04.004
[5]	Marshall R A, Smith E A, Francis M J, et al. A preliminary risk assessment of the Australian region power network to space weather[J]. Space Weather, 2011, 9(10): 1-18.
[6]	NERC. High-impact, low-frequency event risk to the North American bulk power system[R/OL]. http://www.nerc.com.
[7]	NERC. 2012 special reliability assessment interim report—Effects of geomagnetic disturbances on the bulk power system[R/OL]. http://www.nerc.com/pa/RAPA/ra/Pages/default.aspx.
[8]	吴伟丽, 刘连光, 王开让. 磁暴扰动下电力系统故障风险评估方法与模型[J]. 中国电机工程学报, 2015, 35(4): 830-839. doi: 10.13334/j.0258-8013.pcsee.2015.04.009 Wu Weili, Liu Lianguang, Wang Kairang. Risk assessment methods and models of power system fault due to geomagnetic disturbance. Proceedings of the CSEE, 2015, 35(4): 830-839 doi: 10.13334/j.0258-8013.pcsee.2015.04.009
[9]	吴伟丽. 磁暴诱发电网故障灾害风险分析研究进展[J]. 科学技术与工程, 2016, 16(9): 135-141. doi: 10.3969/j.issn.1671-1815.2016.09.022 Wu Weili. Review of risk analysis for severe grid accident due to geomagnetic storm. Science Technology and Engineering, 2016, 16(9): 135-141 doi: 10.3969/j.issn.1671-1815.2016.09.022
[10]	Horton R, Boteler D H, Pirjola R, et al. A test case for the calculation of geomagnetically induced currents[J]. IEEE Trans Power Delivery, 2012, 27(4): 2368-2373. doi: 10.1109/TPWRD.2012.2206407
[11]	刘青, 韩康康, 徐婷. 新疆2020年规划电网地磁感应电流的分布规律及敏感性分析[J]. 电网技术, 2017, 41(11): 3678-3684. doi: 10.13335/j.1000-3673.pst.2017.1199 Liu Qing, Han Kangkang, Xu Ting. Analysis of distribution regularities and sensitivity of geomagnetically induced currents in planned Xinjiang 750 kV power grid. Power System Technology, 2017, 41(11): 3678-3684 doi: 10.13335/j.1000-3673.pst.2017.1199
[12]	Overbye T J, Hutchins T R, Shetye K, et al. Integration of geomagnetic disturbance modeling into the power flow: a methodology for large-scale system studies[C]//IEEE North American Power Symposium, 2012.
[13]	吴伟丽, 刘连光. 克服磁暴的变压器集群无功损耗优化控制方法[J]. 电力系统自动化, 2014, 38(4): 32-37. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201404006.htm Wu Weili, Liu Lianguang. An optimal control method for overcoming clustering transformer reactive power losses due to geomagnetic storm. Automation of Electric Power Systems, 2014, 38(4): 32-37 https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201404006.htm
[14]	刘文颖, 王佳明, 谢昶. 基于脆性风险熵的复杂电网连锁故障脆性源辨识模型[J]. 中国电机工程学报, 2012, 32(31): 142-148. https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201231018.htm Liu Wenying, Wang Jiaming, Xie Chang. Brittleness source identification model for cascading failure of complex power grid based on brittle risk entropy. Proceedings of the CSEE, 2012, 32(31): 142-148 https://www.cnki.com.cn/Article/CJFDTOTAL-ZGDC201231018.htm
[15]	韦琦, 金鸿章, 郭健. 基于脆性的复杂系统研究[J]. 系统工程学报, 2004, 19(3): 326-328. doi: 10.3969/j.issn.1000-5781.2004.03.019 Wei Qi, Jin Hongzhang, Guo Jian. Research on complex system based on brittleness. Journal of System Engineering, 2004, 19(3): 326-328 doi: 10.3969/j.issn.1000-5781.2004.03.019
[16]	Lin Deming, Jin Hongzhang, Li Qi. The brittleness model of complex system based on cellular automata[J]. Journal of Marine Science and Application, 2004, 3(2): 69-72. doi: 10.1007/BF02894337
[17]	Wu Hongmei, Jin Hongzhnag, Lin Panxiang. Risk analysis of complex system brittleness[J]. Systems Engineering and Electronics, 2008, 30(10): 2019-2022. doi: 10.3321/j.issn:1001-506X.2008.10.047
[18]	谢绍宇, 王秀丽, 王锡凡, 等. 考虑网损及电压约束的发输电系统可靠性评估[J]. 电力系统自动化, 2011, 35(2): 1-5. https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201102002.htm Xie Shaoyu, Wang Xiuli, Wang Xifan, et al. Composite system reliability evaluation considering network loss and voltage constraints. Automation of Electric Power Systems, 2011, 35(2): 1-5 https://www.cnki.com.cn/Article/CJFDTOTAL-DLXT201102002.htm
[19]	赵渊, 周家启, 刘洋. 发输电组合系统可靠性评估中的最优负荷削减模型分析[J]. 电网技术, 2004, 28(10): 34-37. https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200410008.htm Zhao Yuan, Zhou Jiaqi, Liu Yang. Analysis on optimal load shedding model in reliability evaluation of composite generation and transmission system. Power System Technology, 2004, 28(10): 34-37 https://www.cnki.com.cn/Article/CJFDTOTAL-DWJS200410008.htm
[20]	IEEE reliability test system task force of the applications of probability methods subcommittee. IEEE reliability test system[J]. IEEE Trans Power Apparatus and Systems, 1979, 98(6): 2047-2054.