Realizing high efficiency spectral beam combining with dual-gratings based on conical diffraction
-
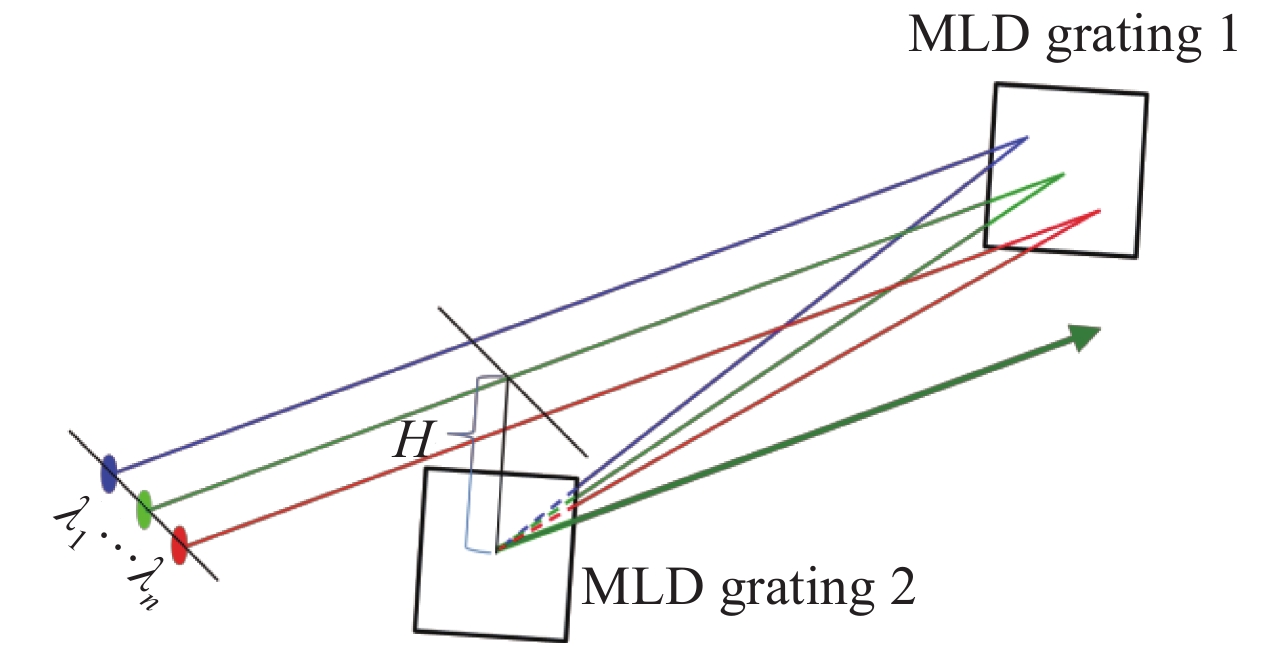
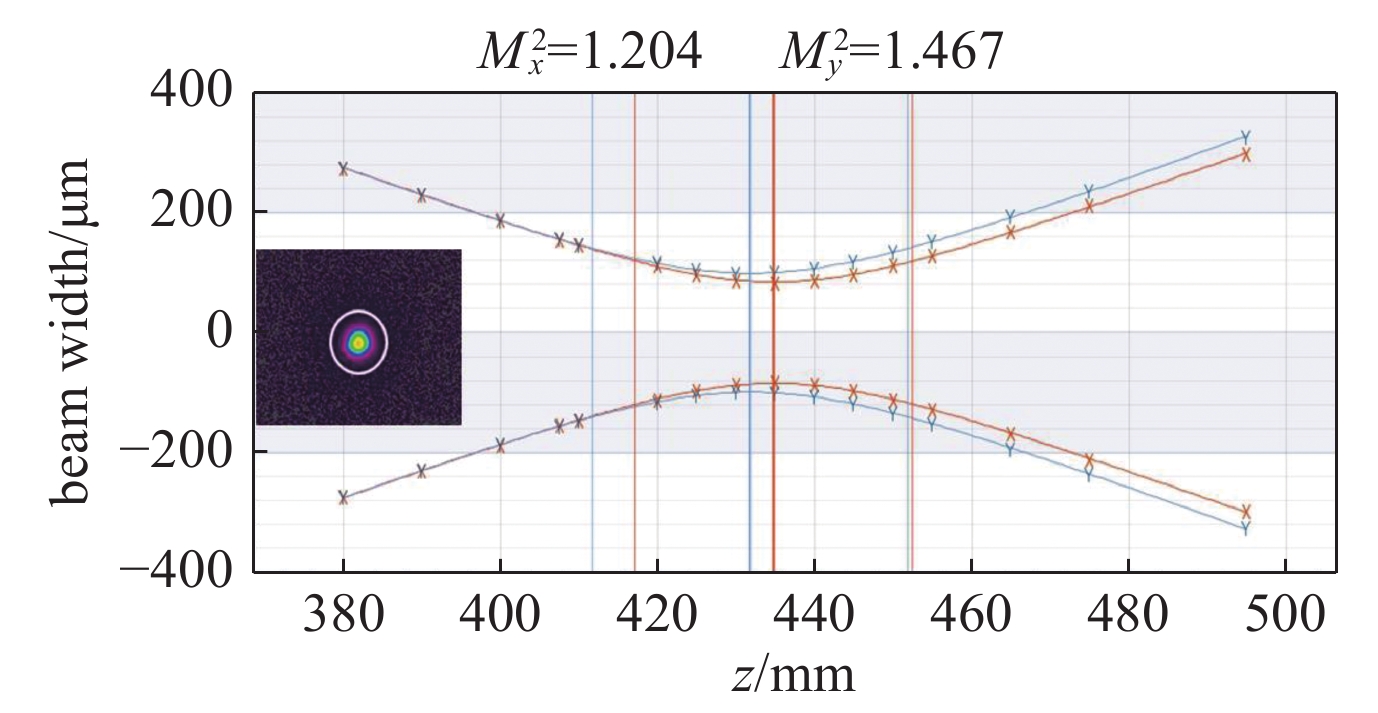
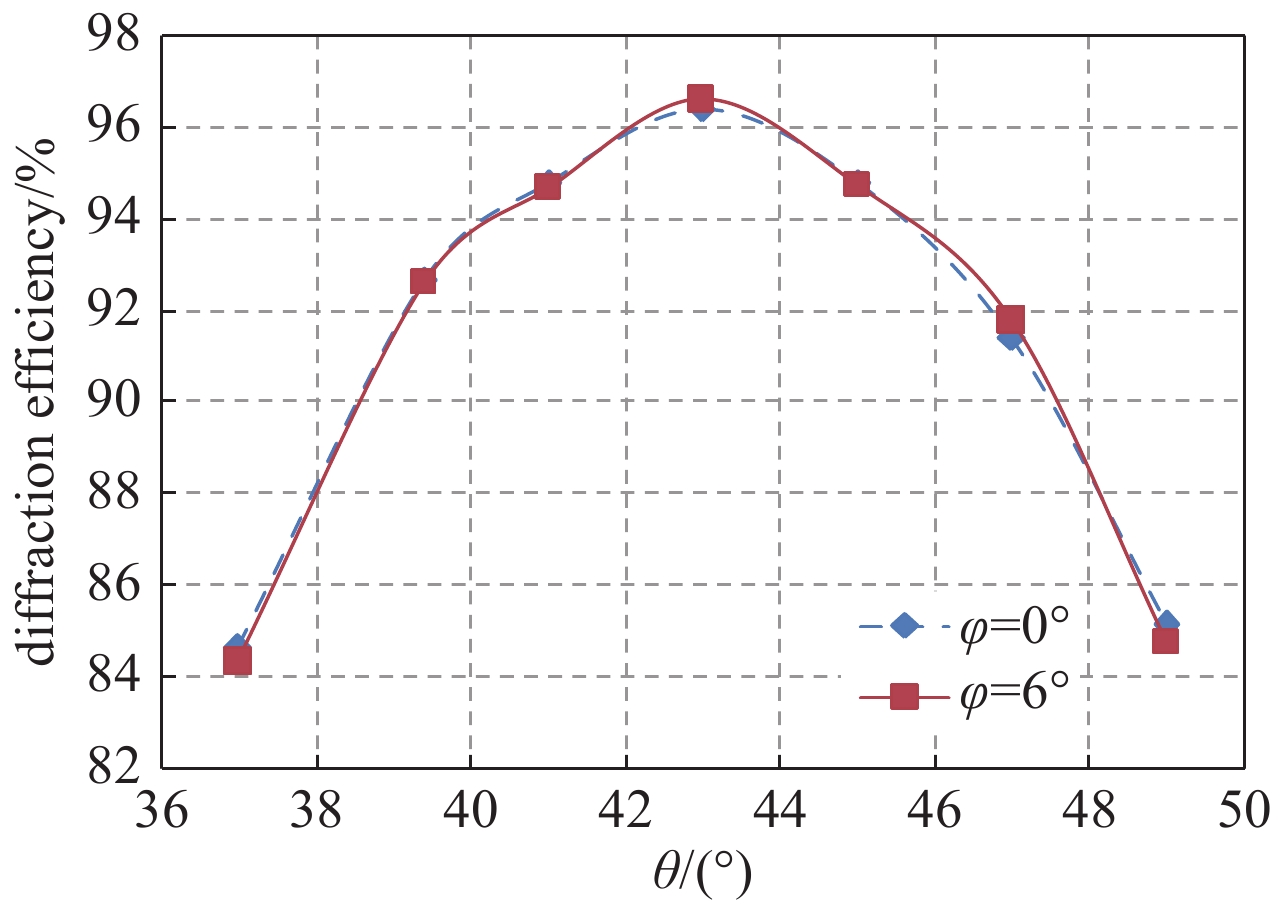
摘要: 分析了基于锥面衍射的双光栅光谱合成系统的可行性，设计了激光入射角为Littrow角附近的双多层介质膜（MLD）光栅光谱合成系统，开展了两路合成实验。当入射极角等于自准直入射角，入射方位角为6°时，光栅衍射效率近似等于光束自准直入射时的衍射效率。基于锥面衍射原理，对中心波长为1050.24 nm和1064.33 nm的两束光纤激光子束进行合成，入射极角为43.99°，测得合成效率为92.9%，较基于非锥面衍射的双光栅光谱合成系统的合成效率提高了8.8%；测得合成光斑光束质量Mx2＝1.204，My2＝1.467，与基于非锥面衍射的双光栅光谱合成系统输出光斑光束质量基本一致。Abstract: The feasibility of realizing high efficiency spectral beam combining with multilayer dielectric (MLD) gratings based on conical diffraction was analyzed. The spectral beam combining approach was designed with the incident polar angle nearly equals to the Littrow angle based on the conical diffraction theory and two unit beams were experimentally combined. The experimental results indicate that, the diffraction efficiency nearly did not change in the case of conical diffraction when θ was constant and
$ \varphi $ ＝6°. The combining efficiency of the output beam which was composited by two unit beams (wavelength equals to 1050.24 nm and 1064.33 nm respectively) with incident polar angle θ of 43.99° was 92.9%, 8.8% higher than that of approach based on non-conical diffraction. The beam quality factor after combining were Mx2＝1.204 and My2＝1.467, which were almost equivalent to that of approach based on non-conical diffraction. -
图 1 光栅结构及入射光角度示意图
Figure 1. Structure of the grating and angle of incident wave vector
图 2 基于锥面衍射的双MLD光栅光谱合成示意图
Figure 2. Schematic of the spectral combining approach with dual-MLD-grating based on conical diffraction
图 4 双光栅锥面衍射光谱合成系统
Figure 4. Picture of the spectral combining approach with dual-MLD-grating based on conical diffraction
图 5 双光栅锥面衍射光谱合成系统输出光束M2实测曲线
Figure 5. Beam quality measured after the combining based on conical diffraction
图 6 基于非锥面衍射的光谱合成系统输出光束M2实测曲线
Figure 6. Beam quality measured after the approach based on non-conical diffraction
图 7 锥面衍射和非锥面衍射下光栅衍射效率随入射角度变化曲线
Figure 7. Change of diffraction efficiency with different incident angle under non-conical diffraction
表 1 一组双MLD光栅锥面衍射合成系统参数理论值
Table 1. Academic value of spectral combining approach with dual-MLD-grating based on conical diffraction
No. unit beam wavelength/nm unit beam interval/mm θ/(°) φ/(°) L/mm Hi/mm Δyi/mm 1 1050.24 0 43.99 5.77 756 −147.654 0.042 2 1051.28 1.9 43.99 5.77 756 −147.659 0.037 3 1052.31 3.8 43.99 5.77 756 −147.665 0.031 4 1053.35 5.7 43.99 5.77 756 −147.67 0.025 5 1054.37 7.6 43.99 5.77 756 −147.676 0.019 6 1055.39 9.5 43.99 5.77 756 −147.682 0.013 7 1056.4 11.4 43.99 5.77 756 −147.689 0.007 8 1057.41 13.3 43.99 5.77 756 −147.696 0 9 1058.41 15.2 43.99 5.77 756 −147.703 −0.007 10 1059.41 17.1 43.99 5.77 756 −147.71 −0.014 11 1060.4 19.0 43.99 5.77 756 −147.717 −0.022 12 1061.39 20.9 43.99 5.77 756 −147.725 −0.029 13 1062.38 22.8 43.99 5.77 756 −147.733 −0.037 14 1063.35 24.7 43.99 5.77 756 −147.741 −0.045 15 1064.33 26.6 43.99 5.77 756 −147.749 −0.054 
下载: 导出CSV
表 2 基于锥面衍射和非锥面衍射的双光栅光谱合成系统的合成效率对比
Table 2. Combining efficiency of the spectral combining approach under the conical diffraction and non-conical diffraction
No. θ/(°) φ/(°) input power/mW output power/mW combining efficiency/% diffraction type 1 43.99 5.77 23.22 21.57 92.9 conical diffraction 2 47.00 0 23.22 19.53 84.1 non-conical diffraction
下载: 导出CSV
-
[1] Pratheepan M, Jander D R, Brooks C D, et al. Dual-grating spectral beam combination of high-power fiber lasers[J]. IEEE J Select Top Quantum, 2009, 15(2): 337-343. doi: 10.1109/JSTQE.2008.2012266 [2] Wirth C, Schmidt O, Tsybin I, et al. High average power spectral beam combining of four fiber amplifiers to 8.2 kW[J]. Opt Lett, 2011, 36(16): 3118-3120. doi: 10.1364/OL.36.003118 [3] Ma Yi, Yan Hong, Peng Wanjing, et al. 9.6 kW common aperture spectral beam combination system based on multi-channel narrow-linewidth fiber lasers[J]. Chinese Journal of Lasers, 2016, 43: 0901009. doi: 10.3788/CJL201643.0901009 [4] Chen Xu, Li Chaoming, Chen Xinrong, et al. Design of multilayer film polarization-independent gratings[C]//Proc of SPIE. 2019: 11336OF. [5] Tian Fei, Yan Hong, Chen Li, et al. Investigation on the influence of spectral linewidth broadening on the beam quality in spectral beam combination[C]//Proc of SPIE. 2014: 92553N. [6] Liu Quan, Jin Yunxia, Wu Jianhong, et al. Fabrication of the polarization independent spectral beam combining grating[C]//Proc of SPIE. 2017: 1025514. [7] Shen Biyao, Zeng Lijiang, Li Lifeng, et al. Fabrication of polarization independent gratings made on multilayer dielectric thin film substrates[J]. High Power Laser and Particle Beams, 2015, 27: 111013. [8] Chen Junming, Zhang Yibing, Wang Yonglu, et al. Polarization-independent broadband beam combining grating with over 98% measured diffraction efficiency from 1023 to 1080 nm[J]. Optics Letters, 2017, 42(19): 4016-4019. doi: 10.1364/OL.42.004016 [9] Mao Xinyu, Li Chaoming, Qiu Keqiang, et al. Design and fabrication of 1300-line/mm polarization-independent reflection gratings for spectral beam combining[J]. Opt Commun, 2020, 458: 124883. doi: 10.1016/j.optcom.2019.124883 [10] James E H, Richard N P. Understanding diffraction grating behavior: including conical diffraction and Rayleigh anomalies from transmission gratings[J]. Opt Eng, 2019, 58: 087105. [11] Bayanheshig, Qi Xiangdong, Tang Yuguo, et al. The vector diffraction theory analysis of chromatic dispersion characteristics of phase grating[J]. Acta Physica Sinica, 2003, 52(5): 1157-1161. -
点击查看大图
计量
- 文章访问数: 1451
- HTML全文浏览量: 358
- PDF下载量: 100
- 被引次数: 0
