机器人气囊抛光去除函数稳定性分析

林泽文; 王振忠; 黄雪鹏; 孔刘伟

doi:10.11884/HPLPB202133.200293

机器人气囊抛光去除函数稳定性分析

doi: 10.11884/HPLPB202133.200293

林泽文^{1, 2,},
王振忠^{1, 2, ,},
黄雪鹏^{1, 2},
孔刘伟²

1.
厦门大学机电工程系，福建厦门 361005
2.
厦门大学深圳研究院，广东深圳 518057

基金项目: 深圳科技计划项目（JCYJ2018030617）

详细信息

作者简介:
林泽文（1995—），男，硕士，从事机器人精密抛光研究

通讯作者:
王振忠（1981—），男，博士，从事先进光学制造研究

中图分类号: TH161
计量
- 文章访问数: 1735
- HTML全文浏览量: 483
- PDF下载量: 64
- 被引次数: 2
出版历程
- 收稿日期: 2020-10-26
- 修回日期: 2021-04-02
- 网络出版日期: 2021-04-20
- 刊出日期: 2021-05-20

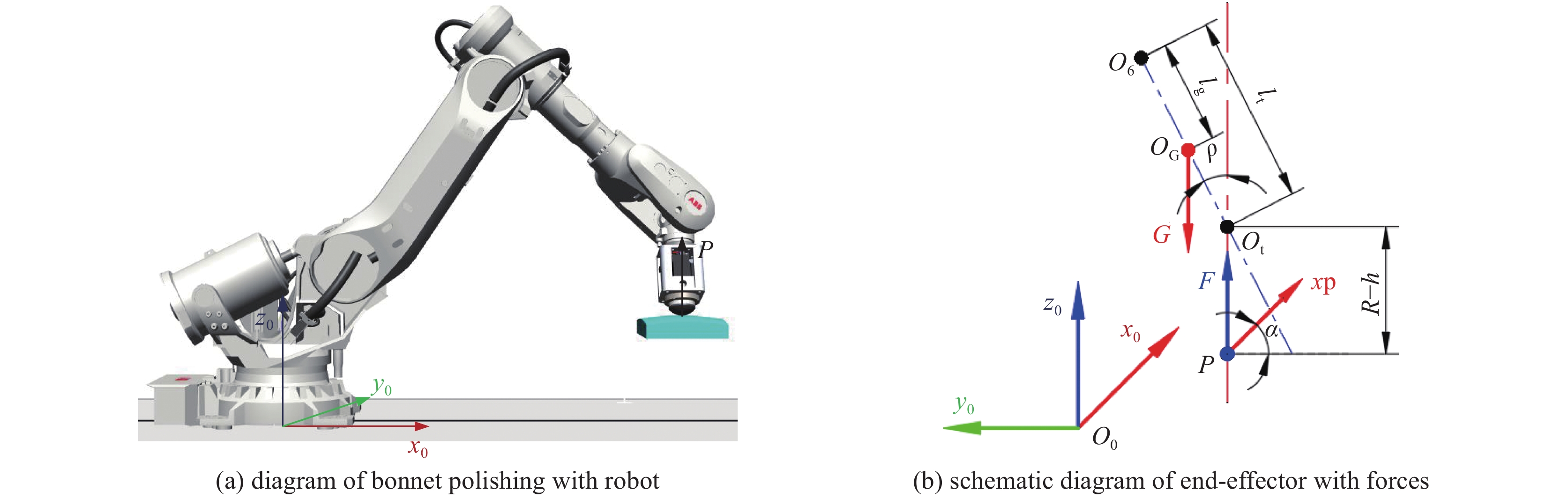
Influence of robotic structural deformation on bonnet polishing removal function

Lin Zewen^{1, 2
,},
Wang Zhenzhong^{1, 2
, ,},
Huang Xuepeng^{1, 2},
Kong Liuwei²

1.
Xiamen University, Xiamen 361005, China
2.
Shenzhen Research Institute of Xiamen University, Shenzhen 518057, China

摘要

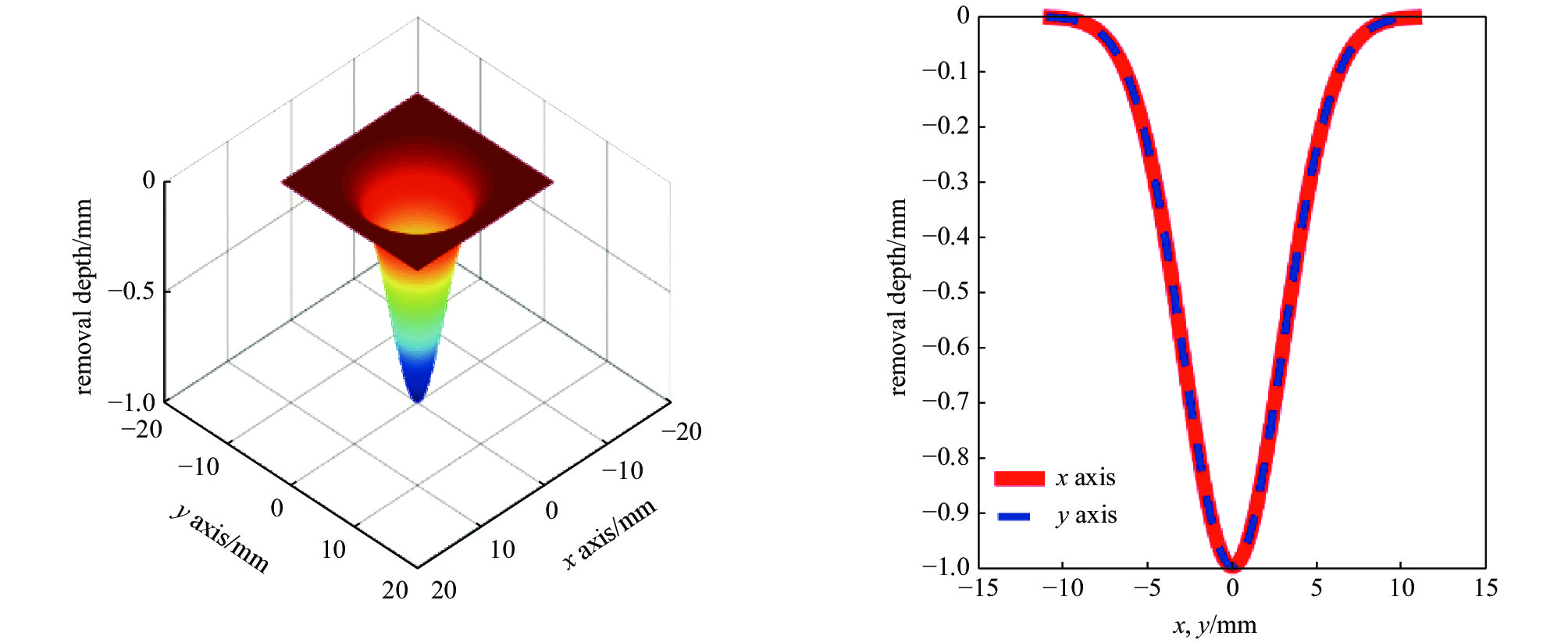
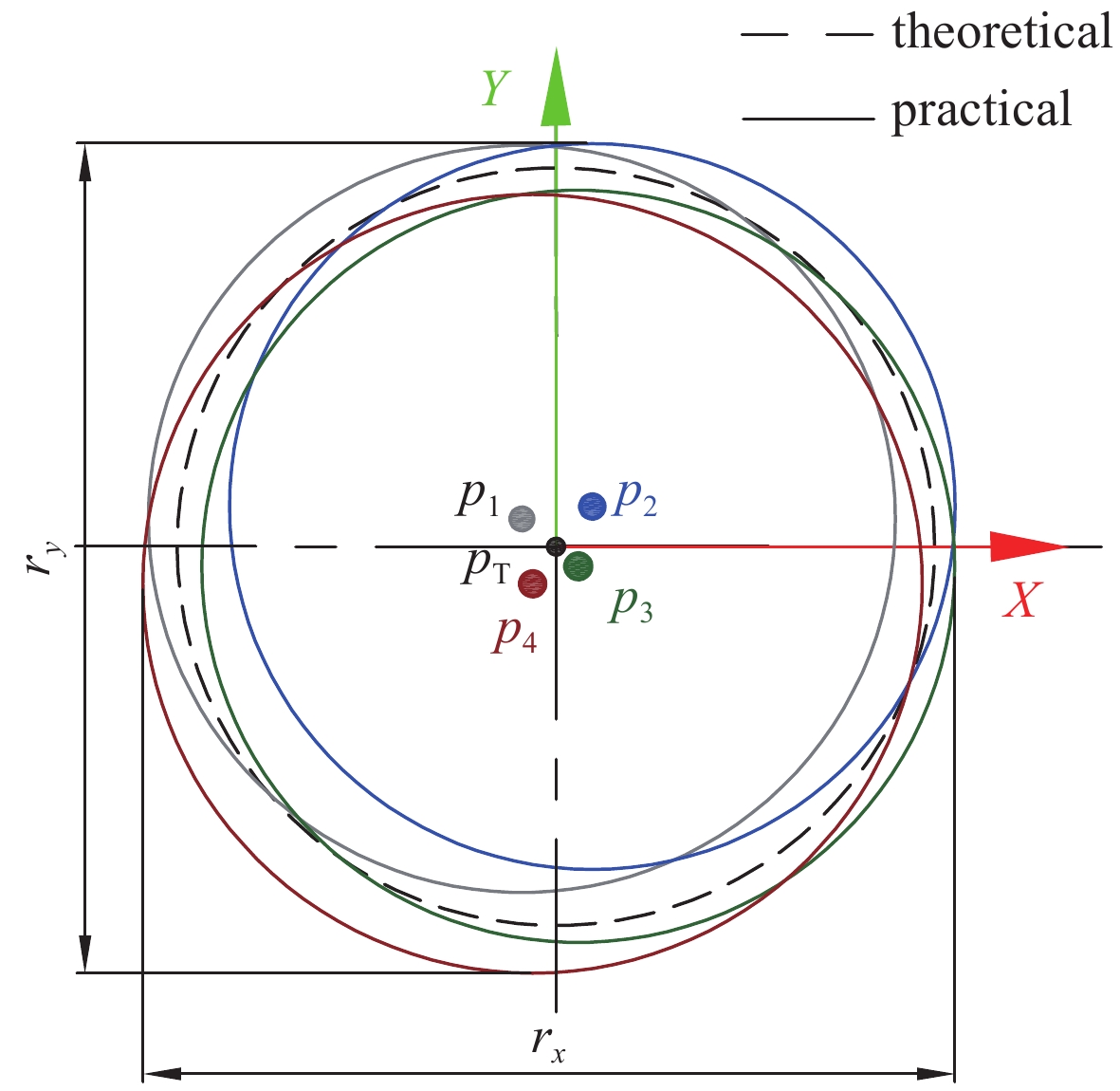
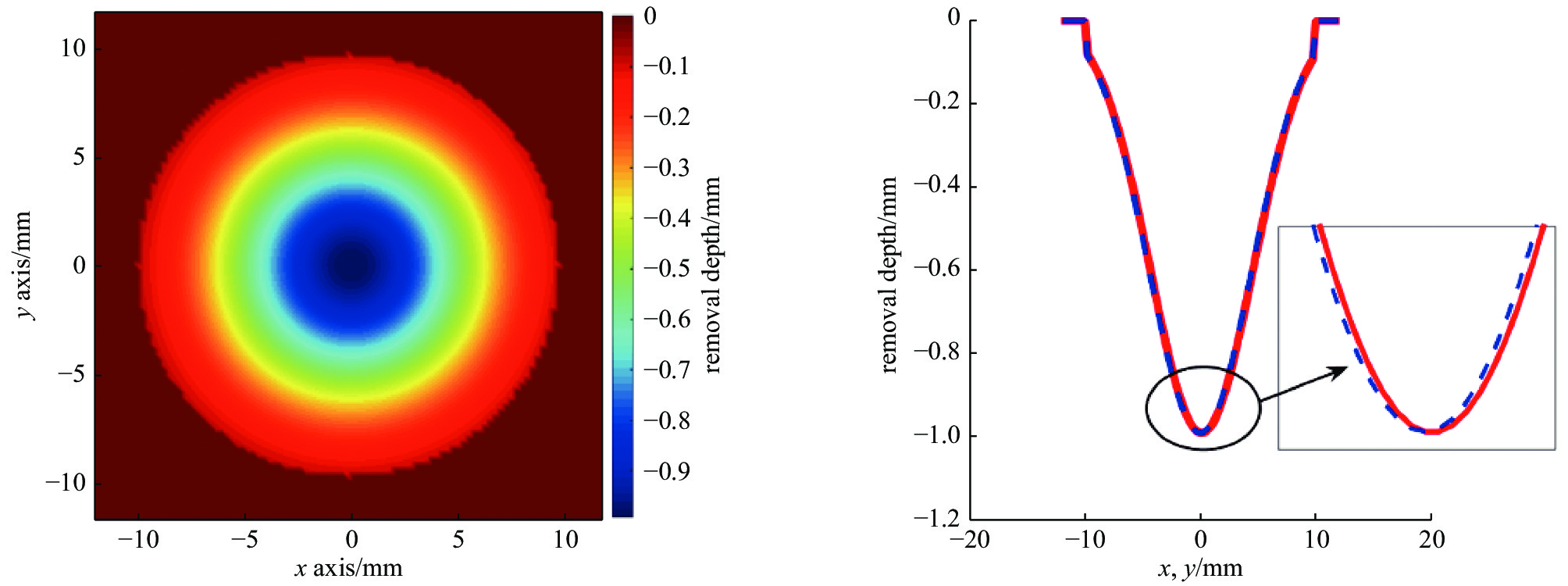
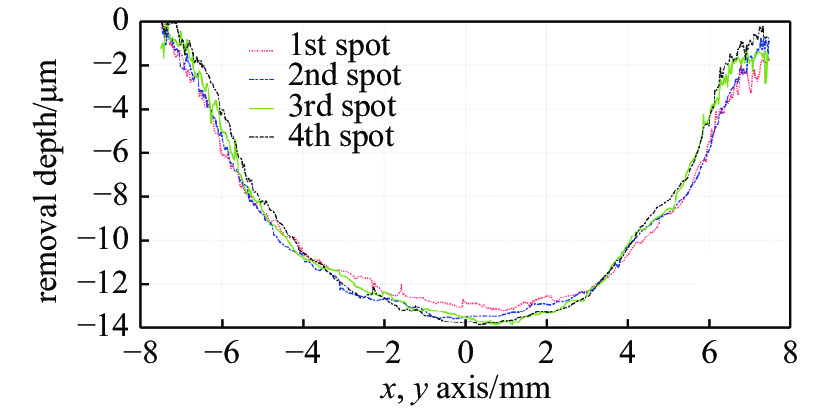
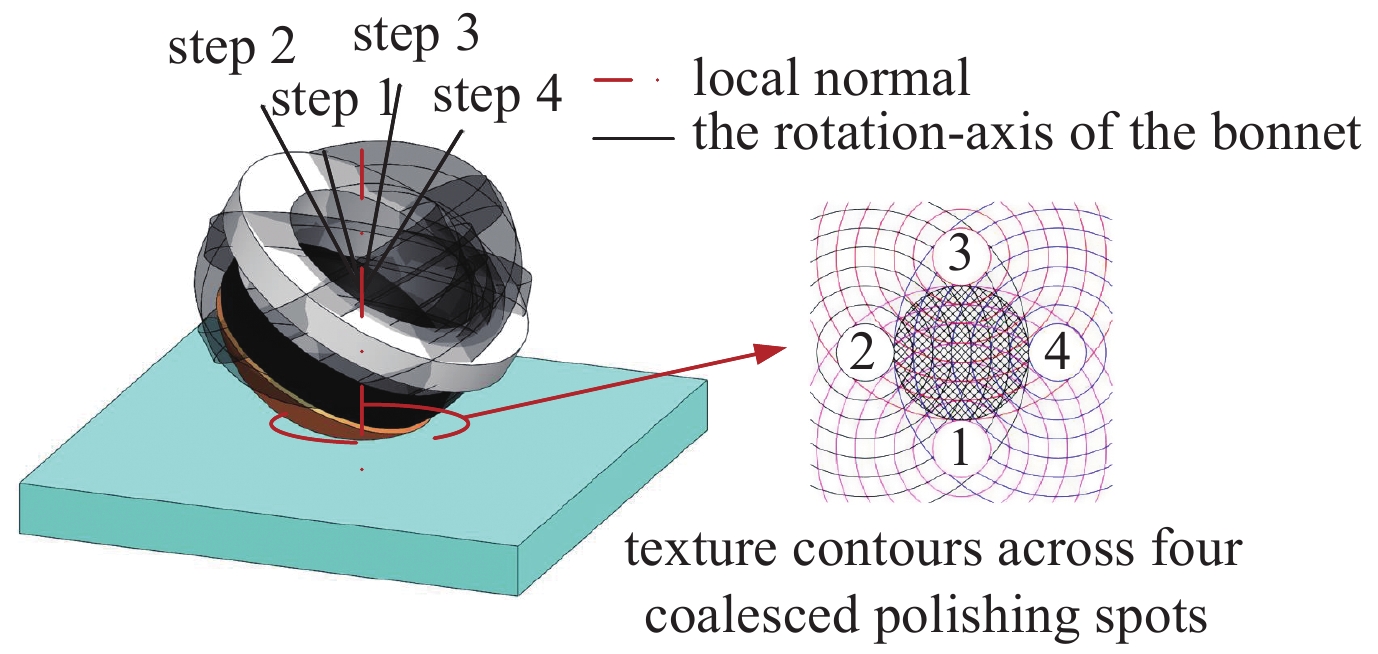
摘要: 基于气囊抛光技术和工业机器人平台开发光学元件精密抛光系统，既能满足光学元件快速抛光环节的高效率和高精度的要求，又可以降低开发成本，是极具潜力的抛光设备开发方案。气囊抛光具有稳定的且确定的材料去除特性，通常要求抛光斑稳定性在90%左右。针对机器人气囊抛光系统在多步离散进动抛光过程中机器人末端刚度对气囊抛光稳定性的影响展开研究，通过建立机器人末端刚度矩阵，获得机器人末端变形；基于Preston理论，建立含变形误差的气囊抛光去除函数。最后设计4步离散定点抛光实验验证机器人气囊抛光系统稳定性。根据结果可知抛光斑在XY截面轮廓线上皆呈类高斯形状，且XY截面轮廓线基本一致，具有比较好的重合度；对比不同抛光位置的截面轮廓线，其相对误差小于5%，由此可验证机器人气囊抛光系统在离散进动抛光时具有较好的稳定性。
- 气囊抛光 /
- 工业机器人 /
- 刚度矩阵 /
- 去除函数 /
- 抛光实验
Abstract: Precision polishing system for opticals based on bonnet polishing technology and industrial robot can not only meet the requirements of high efficiency and precision of rapid polishing, but also reduce the development cost, thus it is a potential development solution for polishing. Bonnet polishing requires stable and deterministic material removal characteristics, and the stability of polishing spot is usually around 90%. The influence of robot stiffness on the stability of robot bonnet polishing system in the process of multi-step discrete precession polishing was studied. The robot end deformation was analyzed by the stiffness matrix, and the removal function of bonnet polishing with deformation error was established based on Preston theory. Finally, a four-step discrete polishing experiment was designed. According to the results, the polishing spot was Gaussian on the xy section contour line, and the xy section contour line was basically the same, with a good coincidence degree. Comparison of the cross-section profiles at different polishing positions indicates, the relative errors are below 5%. The experiment proves that the robot bonnet polishing system has a good stability in discrete precast polishing.
- bonnet polishing /
- industrial robot /
- stiffness matrix /
- removal function /
- polishing experiment

HTML全文

图 1 气囊离散进动抛光示意图

Figure 1. Schematic diagram of bonnet discrete precession polishing

下载: 全尺寸图片幻灯片

图 2 气囊抛光机器人末端受力分析

Figure 2. Force analysis on the end of the bonnet polishing robot

下载: 全尺寸图片幻灯片

图 3 气囊进动抛光速度模型

Figure 3. Bonnet precession polishing speed model

下载: 全尺寸图片幻灯片

图 4 气囊抛光接触区域压力分布仿真

Figure 4. Simulation of pressure distribution in the bonnet polishing contact area

下载: 全尺寸图片幻灯片

图 5 接触区抛光压力仿真拟合结果

Figure 5. Simulation fitting results of polishing pressure in contact area

下载: 全尺寸图片幻灯片

图 6 去除函数仿真建模

Figure 6. Simulation modeling of removal function

下载: 全尺寸图片幻灯片

图 7 结构变形对抛光区域影响示意图

Figure 7. Schematic diagram of the influence of structural deformation on the polishing area

下载: 全尺寸图片幻灯片

图 8 接触压力测量

Figure 8. Contact pressure measurement system

下载: 全尺寸图片幻灯片

图 9 考虑末端变形的实际去除函数仿真结果

Figure 9. Simulation result of actual removal function considering end deformation

下载: 全尺寸图片幻灯片

图 10 不同抛光斑测量结果

Figure 10. Measurement results of polishing spots

下载: 全尺寸图片幻灯片

图 11 不同位置抛光区域x方向轮廓线对比

Figure 11. Comparison of x-direction contour lines of polishing area at different positions

下载: 全尺寸图片幻灯片

表 2 机器人末端变形理论计算结果

Table 2. Theoretical calculation results of robot end deformation

four × 90° steps	x direction/mm	y direction/mm	z direction/mm	whole deformation/mm
0°	0.1206	0	−0.2710	0.2966
90°	0.1221	0.0003	−0.2778	0.3034
180°	0.1238	0	−0.2846	0.3103
270°	0.1221	−0.0003	−0.2778	0.3034

下载: 导出CSV

表 1 机器人4步定点抛光关节转角

Table 1. Robot fixed-point polishing joint angle in four steps

four × 90°steps	${\theta }_{1}$ /（°）	${\theta }_{2}$ /（°）	${\theta }_{3}$ /（°）	${\theta }_{4}$ /（°）	${\theta }_{5}$ /（°）	${\theta }_{6}$ /（°）
0°	0	32.36	14.80	0	22.84	0
90°	−4.41	39.06	3.48	25.65	51.99	−21.17
180°	0	45.76	−8.29	0	72.53	0
270°	4.41	39.06	3.48	−25.65	51.99	21.17

下载: 导出CSV

表 3 气囊抛光有限元仿真设定条件

Table 3. Setting conditions of bonnet polishing finite element simulation

bonnet radius/mm	tool offset/mm	precession angle/(°)	inner pressure/MPa	rotation speed/(r·m⁻¹)
80	0.2，0.6，1	20	0.25	1000

下载: 导出CSV

表 4 接触压力数值拟合结果

Table 4. Numerical fitting results of contact pressure

maximum stress/MPa	standard deviation $\sigma$	modification coefficient $\varphi$
1.708 2	1.231 5	0.175 5

下载: 导出CSV

表 5 气囊抛光实验参数

Table 5. Bonnet polishing experiment parameters

bonnet radius/ mm	precession steps	tool offset/ mm	precession angle/（°）	inner pressure/ MPa	rotational speed/(r·min⁻¹)	dwell time (each step)/s
80	4	0.6	20	0.25	500	20

下载: 导出CSV

表 6 静态压力测量结果

Table 6. Static pressure measurement results (N)

experimental group	F (1st step/0°)	F (2nd step/90°)	F (3rd step/180°)	F (4th step/270°)
1st	105.5	108.7	113.6	105.1
2nd	101.2	106.1	116.6	116.8
3rd	91.4	94.2	103.2	89.3
mean	99.4	103.1	111.1	103.79

下载: 导出CSV

表 7 抛光区域去除深度和相对误差值

Table 7. Polished area removal depth and relative error value

experimental group	removal depth/μm	relative error/%
spot 1	13.249	0
spot 2	13.599	2.64
spot 3	13.864	4.64
spot 4	13.845	4.50

下载: 导出CSV

参考文献(15)

[1]	Bingham R G, Walker D D, Kim D H, et al. Novel automated process for aspheric surfaces[C]//Proceedings of SPIE 4093, Current Developments in Lens Design and Optical Systems Engineering. 2000: 445-450.
[2]	Walker D D, Brooks D, Freeman R, et al. First aspheric form and texture results from a production machine embodying the precession process[C]//Proceedings of SPIE 4451, Optical Manufacturing and Testing IV. San Diego, CA, USA: SPIE, 2001: 267-276.
[3]	Walker D D, Beaucamp A T H, Bingham R G, et al. Precessions aspheric polishing: New results from the development program[C]//Proceedings of SPIE 5180, Optical Manufacturing and Testing V. California, USA: SPIE, 2003: 15-28.
[4]	Walker D D, Brooks D, King A, et al. The “Precessions” tooling for polishing and figuring flat, spherical and aspheric surfaces[J]. Optics Express, 2003, 11(8): 958-964. doi: 10.1364/OE.11.000958
[5]	潘日, 杨炜, 王振忠, 等. 大口径非球面元件可控气囊抛光系统[J]. 强激光与粒子束, 2012, 24(6):1344-1348. (Pan Ri, Yang Wei, Wang Zhenzhong, et al. Controlled bonnet polishing system for large aspheric lenses[J]. High Power Laser and Particle Beams, 2012, 24(6): 1344-1348 doi: 10.3788/HPLPB20122406.1344
[6]	Pan Ri, Wang Zhenzhong, Wang Chunjin, et al. Research on control optimization for bonnet polishing system[J]. International Journal of Precision Engineering and Manufacturing, 2014, 15(3): 483-488. doi: 10.1007/s12541-014-0361-6
[7]	Pan Ri, Wang Zhenzhong, Jiang Tao, et al. A novel method for aspheric polishing based on abrasive trajectories analysis on contact region[J]. Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, 2015, 229(2): 275-285.
[8]	王春锦, 郭隐彪, 王振忠, 等. 光学元件气囊抛光系统动态去除函数建模[J]. 机械工程学报, 2013, 49(17):19-25. (Wang Chunjin, Guo Yinbiao, Wang Zhenzhong, et al. Dynamic removal function modeling of bonnet tool polishing on optics elements[J]. Journal of Mechanical Engineering, 2013, 49(17): 19-25 doi: 10.3901/JME.2013.17.019
[9]	Wang Chunjin, Yang Wei, Wang Zhenzhong, et al. Dwell-time algorithm for polishing large optics[J]. Applied Optics, 2014, 53(21): 4752-4760. doi: 10.1364/AO.53.004752
[10]	Wang Chunjin, Wang Zhenzhong, Pan R, et al. Effect analysis of the residual error evaluation method used in bonnet polishing process for aspheric lens[J]. The International Journal of Advanced Manufacturing Technology, 2013, 69(9): 2505-2511.
[11]	高波, 姚英学, 谢大纲, 等. 气囊抛光进动机构的运动建模与仿真[J]. 机械工程学报, 2006, 42(2):101-104. (Gao Bo, Yao Yingxue, Xie Dagang, et al. Movement modeling and simulation of precession mechanisms for bonnet tool polishing[J]. Chinese Journal of Mechanical Engineering, 2006, 42(2): 101-104
[12]	宋剑锋, 姚英学, 谢大纲. 球面光学零件气囊抛光工艺参数优化的研究[J]. 光学技术, 2014, 40(2):99-104. (Song Jianfeng, Yao Yingxue, Xie Dagang. Research on the optimization of the process parameters of the bonnet polishing the spherical optical parts[J]. Optical Technique, 2014, 40(2): 99-104 doi: 10.3788/GXJS20144002.0099
[13]	Li Hongyu, Walker D, Zheng Xiao, et al. Advanced techniques for robotic polishing of aluminum mirrors[C]//Proceedings of SPIE 10692, Optical Fabrication, Testing, and Metrology VI. 2018: 106920N.
[14]	计时鸣, 金明生, 张宪, 等. 应用于模具自由曲面的新型气囊抛光技术[J]. 机械工程学报, 2007, 43(8):2-6. (Ji Shiming, Jin Mingsheng, Zhang Xian, et al. Novel gasbag polishing technique for free-form mold[J]. Chinese Journal of Mechanical Engineering, 2007, 43(8): 2-6 doi: 10.3901/JME.2007.08.002
[15]	Ji S M, Zhang L, Yuan Q L, et al. A novel ballonet polishing tool and its robot control system for polishing the curved surface of mould[J]. International Journal of Computer Applications in Technology, 2007, 29(2/4): 212-215.