基于远场信息和卷积神经网络的波前重构方法

史宗佳; 向振佼; 杜应磊; 万敏; 顾静良; 李国会; 向汝建; 游疆; 吴晶; 徐宏来

doi:10.11884/HPLPB202133.210040

基于远场信息和卷积神经网络的波前重构方法

doi: 10.11884/HPLPB202133.210040

史宗佳^{1, 2,},
向振佼¹,
杜应磊^1, ,,
万敏¹,
顾静良¹,
李国会¹,
向汝建¹,
游疆^{1, 2},
吴晶¹,
徐宏来¹

1.
中国工程物理研究院应用电子学研究所，四川绵阳 621900
2.
中国工程物理研究院研究生院，北京 100088

基金项目: 中国工程物理研究院创新发展基金项目（CX2020033）；国防科技创新特区课题项目（193A221011101）

详细信息

作者简介:
史宗佳（1995—），男，硕士研究生，从事自适应光学方面的研究

通讯作者:
杜应磊（1988—），男，学士，助理研究员，从事激光系统主动光学技术研究

中图分类号: O439
计量
- 文章访问数: 1413
- HTML全文浏览量: 525
- PDF下载量: 114
- 被引次数: 0
出版历程
- 收稿日期: 2021-02-04
- 修回日期: 2021-04-02
- 网络出版日期: 2021-04-19
- 刊出日期: 2021-08-15

Wavefront reconstruction method based on far-field information and convolutional neural network

1.
Institute of Applied Electronics, CAEP, Mianyang 621900, China
2.
Graduate School of China Academy of Engineering Physics, Beijing 100088, China

摘要

摘要: 探测波前相位信息是实现自适应光学波前补偿的关键，使用卷积神经网络（CNN）代替波前传感器进行波前重构，系统简单易于实现，同时重构过程不依赖迭代运算，快速实时。为准确提取远场中的波前特征，CNN需要事先使用大量样本进行训练。研究中根据4～30阶大气湍流泽尼克像差系数与其远场强度的对应关系，仿真制作样本数据集，训练CNN从输入的一帧远场图像中预测出畸变波前的泽尼克像差系数，重构原始波前。验证结果表明，该方法能快速实时地还原出波前相位信息，重构波前较原始波前具有极高的波面吻合度和较小的残差剩余量，有望实现实际自适应光学系统中的闭环校正。
- 自适应光学 /
- 深度学习 /
- 卷积神经网络 /
- 泽尼克模式 /
- 远场光斑 /
- 波前重构
Abstract: Detecting wavefront phase information is the key to realize adaptive optics wavefront compensation. Using convolutional neural network (CNN) instead of wavefront sensor for wavefront reconstruction, the system can be simple and easy to implement, and the reconstruction process is fast and real-time without iteration. To extract the wavefront features from the far field accurately, CNN needs to use a large number of samples for training in advance. In the study, according to the corresponding relationship between Zernike aberration coefficient of orders 4 to 30 and its far-field intensity, the sample data set was simulated, CNN was trained to predict the Zernike aberration coefficient of the distorted wavefront from an input far-field image, then reconstruct the original wavefront. The experimental results show that this method can restore the phase information of wavefront quickly and in real time. Compared with the original wavefront, the reconstructed wavefront has higher wavefront coincidence and smaller residual. It is expected to realize the closed-loop correction in practical adaptive optics systems.
- adaptive optics /
- deep learning /
- convolutional neural network /
- Zernike model /
- far-field spot /
- wavefront reconstruction

HTML全文

图 1 基于CNN的波前重构系统

Figure 1. Wavefront reconstruction system based on CNN

下载: 全尺寸图片幻灯片

图 2 不同的残差单元

Figure 2. Different residual elements

下载: 全尺寸图片幻灯片

图 3 CNN波前重构流程图

Figure 3. Flow chart of CNN wavefront reconstruction

下载: 全尺寸图片幻灯片

图 4 某一样本远场和波前泽尼克系数

Figure 4. Far-field and wavefront Zernike coefficients of a sample

下载: 全尺寸图片幻灯片

图 5 训练中四种ResNet模型的L1 loss变化过程，（a）图为训练集，（b）图为验证集

Figure 5. The L1 loss change process of the four ResNet models in training is shown in (a) the training set and (b) the verification set

下载: 全尺寸图片幻灯片

图 6 网络的单帧图像预测时间

Figure 6. Single frame image prediction time of ResNet

下载: 全尺寸图片幻灯片

图 7 测试集中某一样本的波前重构结果

Figure 7. Wavefront reconstruction results of a sample in the test set

下载: 全尺寸图片幻灯片

图 8 测试集样本原始波前和波前残差PV和RMS的散点图

Figure 8. Scatter plot of PV and RMS of original wavefront and wavefront residuals of test set samples

下载: 全尺寸图片幻灯片

图 9 测试集样本波前残差与原始波前的PV和RMS比值

Figure 9. Ratio of PV and RMS of sample wavefront residuals to original wavefront of test set

下载: 全尺寸图片幻灯片

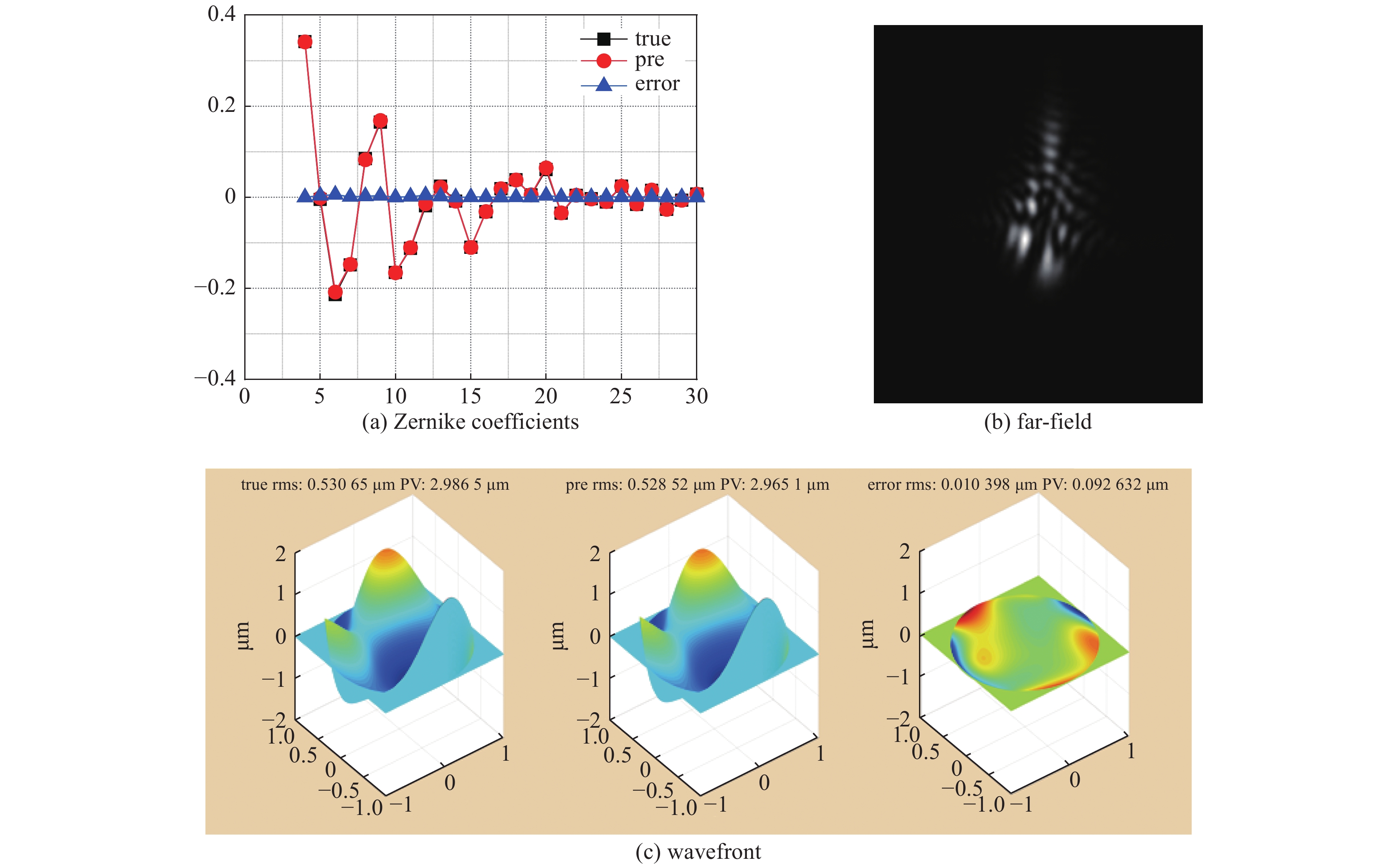
表 1 不同强度湍流的重构波前结果

Table 1. Wavefront reconstruction results of turbulence with different intensities

R₀	far field image size/ pixel	L1 error	normalized coefficient RMSE	PV of the test set samples’ original wavefront/μm	RMS of the test set samples’ original wavefront/μm	PV of reconstructed wavefront residuals/μm	RMS of reconstructed wavefront residuals/μm	residual PV to original wavefront ratio (90% of sample)/%	residual RMS to original wavefront ratio (90% of sample)/%
1	140×140	0.0040	0.0051	2.67±1.63	0.54±0.37	0.12±0.07	0.02±0.01	6	5
0.5	200×200	0.0204	0.0266	5.06±2.76	1.0±0.55	1.14±0.75	0.20±0.13	30	27

下载: 导出CSV

参考文献(19)

[1]	周仁忠. 自适应光学[J]. 中国光学, 1997(5):98-99. (Zhou Renzhong. Adaptive optics[J]. Optics of China, 1997(5): 98-99
[2]	Hardy J W. Adaptive optics: a progress review[C]//Proceedings of SPIE Active and Adaptive Optical Systems. San Diego, CA, USA: SPIE, 1991: 1542.
[3]	Yasuno Y, Wiesendanger T F, Ruprecht A K, et al. Wavefront-flatness evaluation by wavefront-correlation-information-entropy method and its application for adaptive confocal microscope[J]. Optics Communications, 2004, 232(1/6): 91-97.
[4]	母杰, 景峰, 王逍, 等. 相干合成中基于SPGD算法的平移误差和倾斜误差控制[J]. 中国激光, 2014, 41:0602002. (Mu Jie, Jing Feng, Wang Xiao, et al. Error control of piston and tilt based on SPGD in coherent beam combination[J]. Chinese Journal of Lasers, 2014, 41: 0602002 doi: 10.3788/CJL201441.0602002
[5]	Vorontsov M A, Carhart G W, Ricklin J C. Adaptive phase-distortion correction based on parallel gradient-descent optimization[J]. Optics Letters, 1997, 22(12): 907-909. doi: 10.1364/OL.22.000907
[6]	Débarre D, Booth M J, Wilson T. Image based adaptive optics through optimisation of low spatial frequencies[J]. Optics Express, 2007, 15(13): 8176-8190. doi: 10.1364/OE.15.008176
[7]	Kendrick R L, Acton D S, Duncan A L. Phase-diversity wave-front sensor for imaging systems[J]. Applied Optics, 1994, 33(27): 6533-6546. doi: 10.1364/AO.33.006533
[8]	Guo Hong, Korablinova N, Ren Qiushi, et al. Wavefront reconstruction with artificial neural networks[J]. Optics Express, 2006, 14(14): 6456-6462. doi: 10.1364/OE.14.006456
[9]	Nguyen T, Bui V, Lam V, et al. Automatic phase aberration compensation for digital holographic microscopy based on deep learning background detection[J]. Optics Express, 2017, 25(13): 15043-15057. doi: 10.1364/OE.25.015043
[10]	Paine S W, Fienup J R. Machine learning for improved image-based wavefront sensing[J]. Optics Letters, 2018, 43(6): 1235-1238. doi: 10.1364/OL.43.001235
[11]	Nishizaki Y, Valdivia M, Horisaki R, et al. Deep learning wavefront sensing[J]. Optics Express, 2019, 27(1): 240-251. doi: 10.1364/OE.27.000240
[12]	Tian Qinghua, Lu Chenda, Liu Bo, et al. DNN-based aberration correction in a wavefront sensorless adaptive optics system[J]. Optics Express, 2019, 27(8): 10765-10776. doi: 10.1364/OE.27.010765
[13]	马慧敏, 焦俊, 乔焰, 等. 一种基于光强图像深度学习的波前复原方法[J]. 激光与光电子学进展, 2020, 57:081103. (Ma Huimin, Jiao Jun, Qiao Yan, et al. Wavefront restoration method based on light intensity image deep learning[J]. Laser & Optoelectronics Progress, 2020, 57: 081103
[14]	He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al. Deep residual learning for image recognition[C]//IEEE Conference on Computer Vision and Pattern Recognition, 2016: 770-778.
[15]	徐瑞超, 高明. 大气湍流等效相位屏的仿真研究[J]. 西安工业大学学报, 2018, 38(2):108-113. (Xu Ruichao, Gao Ming. Simulation of the equivalent phase screen distorted by atmospheric turbulence[J]. Journal of Xi'an Technological University, 2018, 38(2): 108-113
[16]	Yan Haixing, Li Shushan, Zhang Deliang, et al. Numerical simulation of an adaptive optics system with laser propagation in the atmosphere[J]. Applied Optics, 2000, 39(18): 3023-3031. doi: 10.1364/AO.39.003023
[17]	Lane R G, Glindemann A, Dainty J C. Simulation of a Kolmogorov phase screen[J]. Waves in Random Media, 1992, 2(3): 209-224. doi: 10.1088/0959-7174/2/3/003
[18]	Yang Ping, Ao Mingwu, Liu Yuan, et al. Intracavity transverse modes controlled by a genetic algorithm based on Zernike mode coefficients[J]. Optics Express, 2007, 15(25): 17051-17062. doi: 10.1364/OE.15.017051
[19]	粘伟, 刘兆军, 李博. 大口径空间望远镜变形镜校正能力分析[J]. 科学技术与工程, 2018, 18(23):219-223. (Nian Wei, Liu Zhaojun, Li Bo. Correction quality analysis of deformable mirror for large aperture space telescope[J]. Science Technology and Engineering, 2018, 18(23): 219-223 doi: 10.3969/j.issn.1671-1815.2018.23.030