JASMIN-based fast shielding effectiveness prediction of enclosure containing thin composite layer
-
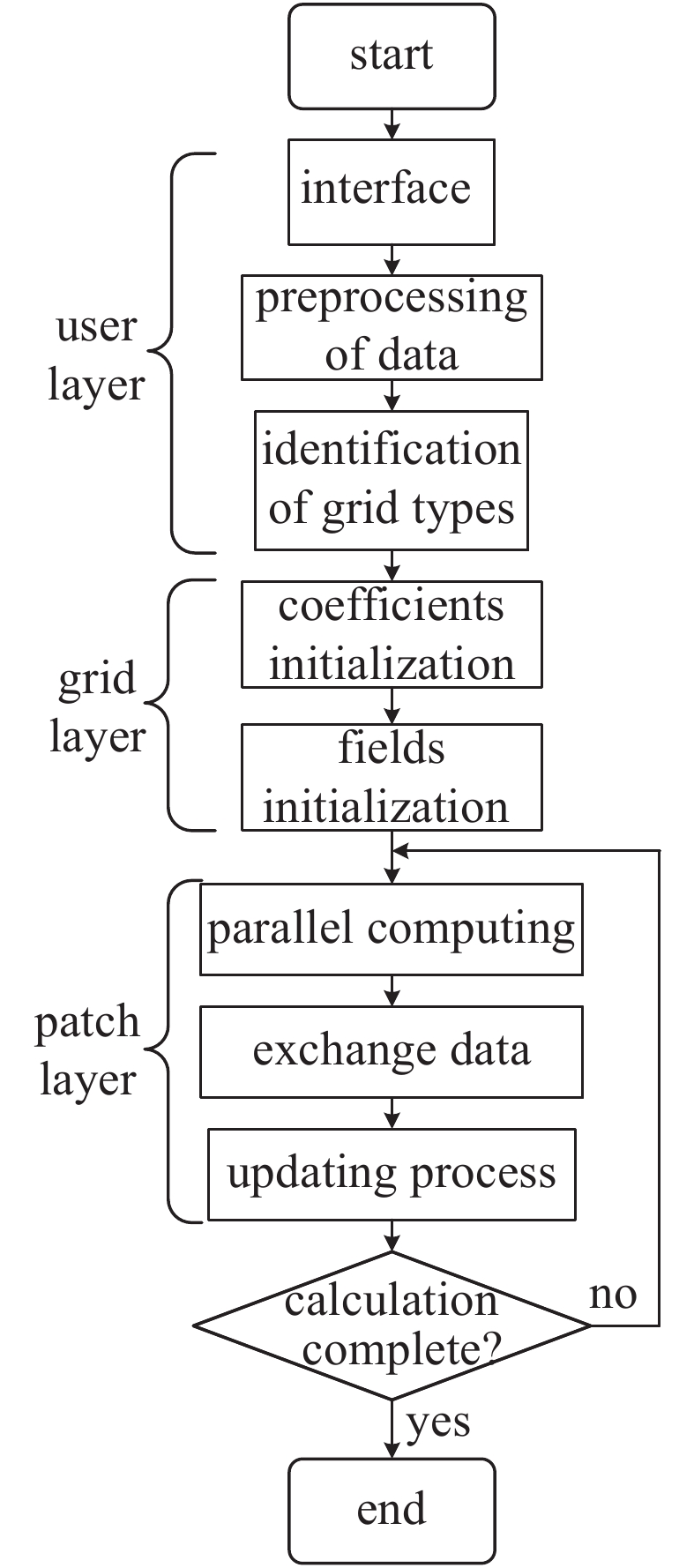
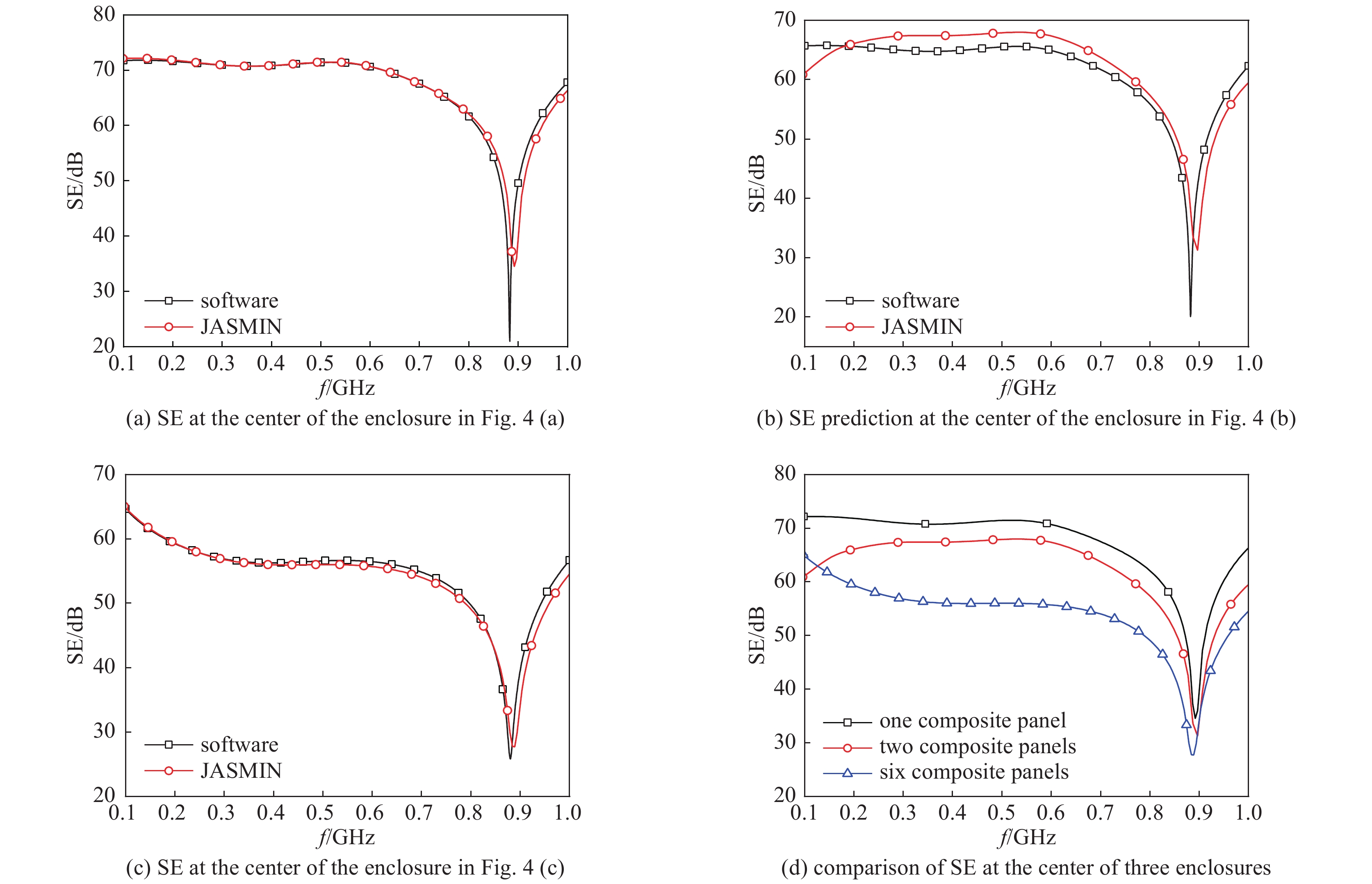
摘要: 在时域有限差分（FDTD）法中采用亚网格边界条件（SGBC）法对复合材料薄层结构进行建模，可以突破复合材料薄层对空间步长的限制从而大大降低计算成本。基于大规模并行化平台JASMIN实现了SGBC-FDTD算法，通过对复合材料薄层结构的自动建模和适配，实现对复合材料薄层的快速并行化处理。利用所开发的并行SGBC-FDTD算法计算分析了含不同电磁特性复合材料薄层方舱在0.1～1.0 GHz内的电磁屏蔽效能，结果表明采用并行SGBC-FDTD算法的计算结果与全波分析软件计算结果吻合完好，且计算效率显著提升。Abstract: The subgridding boundary condition (SGBC) based modeling of thin composite layer in Finite-Difference Time-Domain (FDTD) simulation of enclosures breaks the constraint that the mesh size should be less than the smallest dimension of thin composite layer to get more accurate results, and therefore greatly reduce the computational cost. A large-scale parallelization platform JASMIN based modeling method of SGBC-FDTD was developed. The thin composite layer can be automatically modeled and adaptively allocated in the developed parallelized SGBC-FDTD code. The parallelized SGBC-FDTD algorithm was used to analyze the electromagnetic shielding effectiveness of enclosures containing composite thin layers with different electromagnetic properties in the frequency range of 0.1−1.0 GHz. The results show that shielding effectiveness predicted using the parallelized SGBC-FDTD algorithm are in good agreement with the ones calculated by a full-wave analysis software, while the calculation efficiency is significantly improved.
-
图 1 色散复合材料薄板的SGBC-FDTD算法示意图
Figure 1. Diagram of SGBC-FDTD method for dispersive composite thin slab
图 2 基于JASMIN平台的并行SGBC-FDTD算法流程图
Figure 2. Flow chart of parallelized SGBC-FDTD algorithm on JASMIN platform
图 3 六面为复合材料的方舱计算模型及屏蔽效能
Figure 3. Calculation model and shielding effectiveness (SE) prediction of the enclosure with six composite panels
图 5 非色散复合材料平板的方舱的SE
Figure 5. SE prediction of enclousures containing nondispersive composite panels
图 6 介电常数拟合值与实际值对比
Figure 6. Comparison between fitting values and actual values of permittivity
图 7 色散复合材料方舱的SE
Figure 7. SE prediction of enclosures containing dispersive composite panels
表 1 MAD和
$ \rho $ 随粗细网格步长比的变化Table 1. Variations of MAD and ρ with respect to the step size ratio of coarse (RFC) and fine meshes
RCF MAD/dB $ \rho $ 10 0.5410 0.9962 20 0.5888 0.9964 40 0.6017 0.9965 60 0.6040 0.9965 80 0.6049 0.9965 100 0.6053 0.9965 200 0.6058 0.9965 250 0.6058 0.9965 
下载: 导出CSV
表 2 MAD和ρ随时间步长的变化
Table 2. Variations of MAD and ρ with respect to time step
a MAD/dB $ \rho $ 0.4 0.5874 0.9963 0.5 0.5864 0.9965 0.6 0.5925 0.9965 0.7 0.6040 0.9965 0.8 0.6025 0.9965 0.9 0.6041 0.9965
下载: 导出CSV
表 3 拟合得到留数与极点
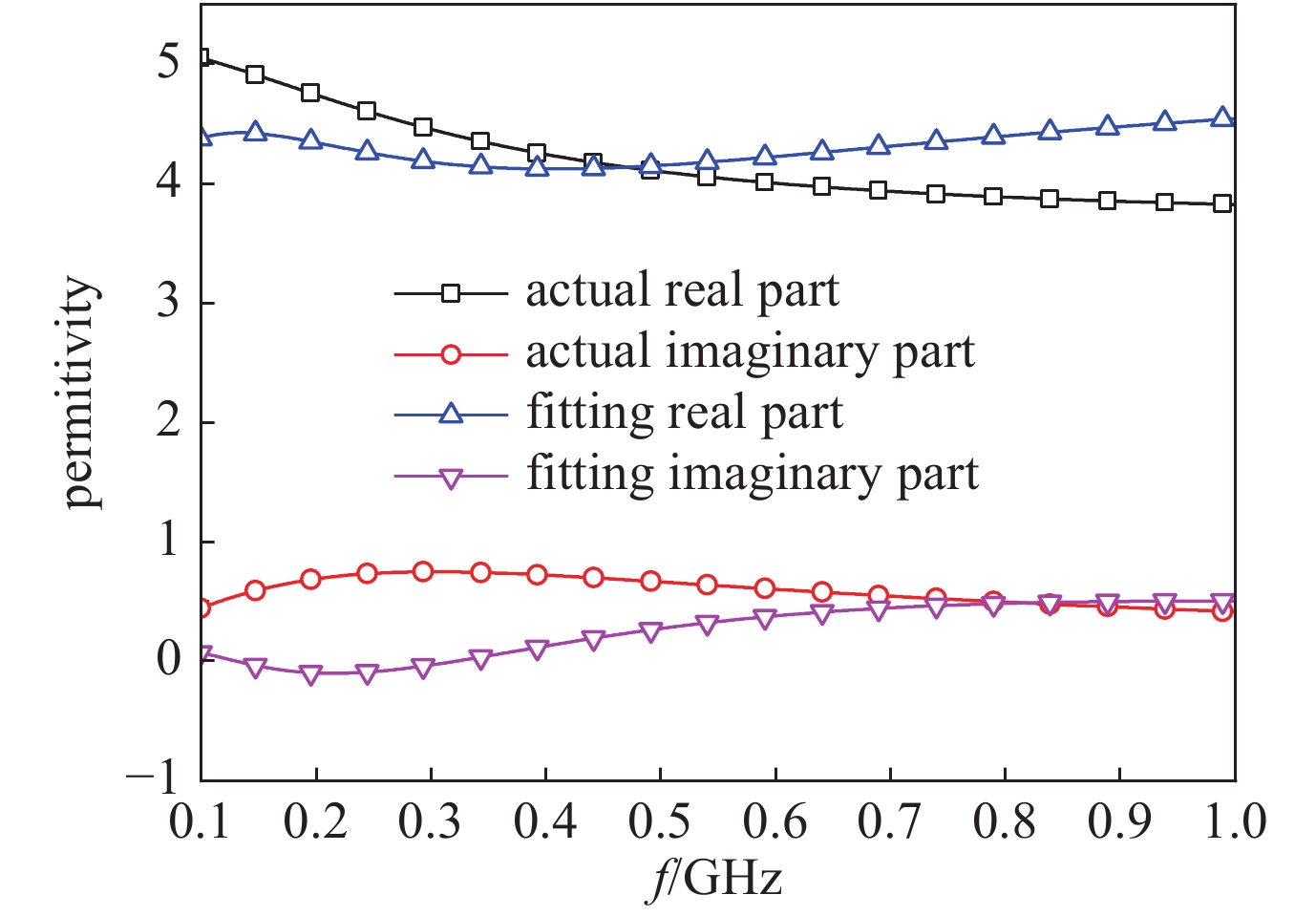
Table 3. Residues and poles obtained by vector fitting
$ {R_{{\rm{\varepsilon }},k}}$ $ {p_{{\rm{\varepsilon }},k}}$ −9.993＋0.0j −3.737＋0.0j 5.129＋0.0j −1.898＋0.0j −2.194＋0.0j −0.323＋0.0j 1.699＋0.0j −0.253＋0.0j
下载: 导出CSV
表 4 软件与SGBC-FDTD的计算成本对比
Table 4. Comparison of calculation cost between commercial software and SGBC-FDTD
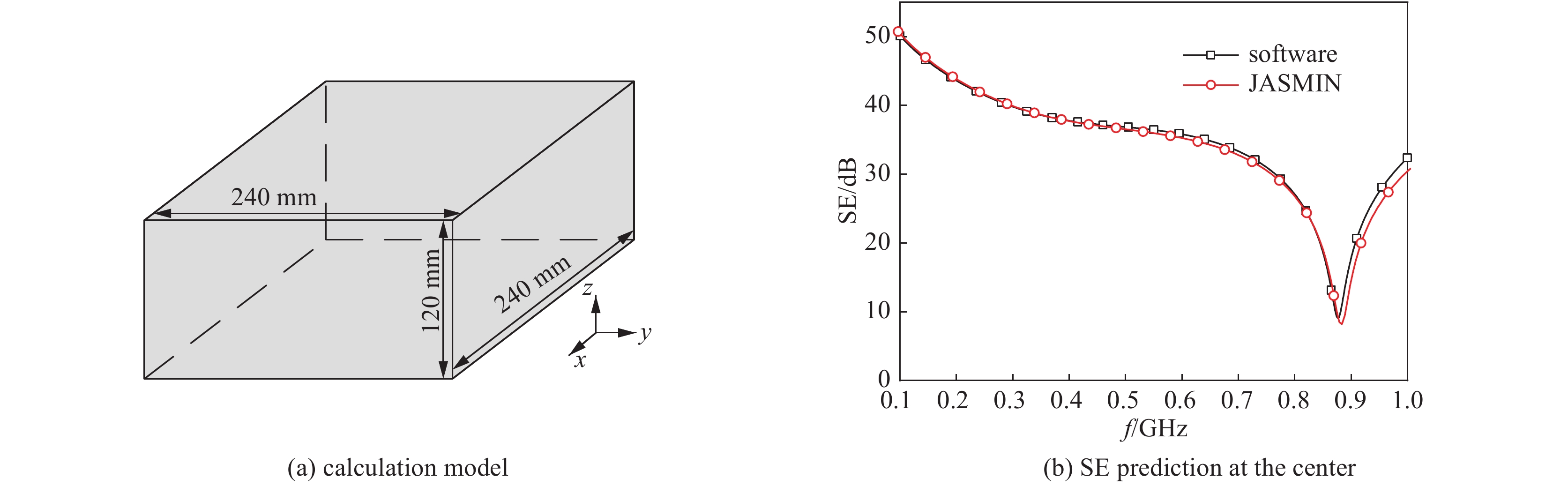
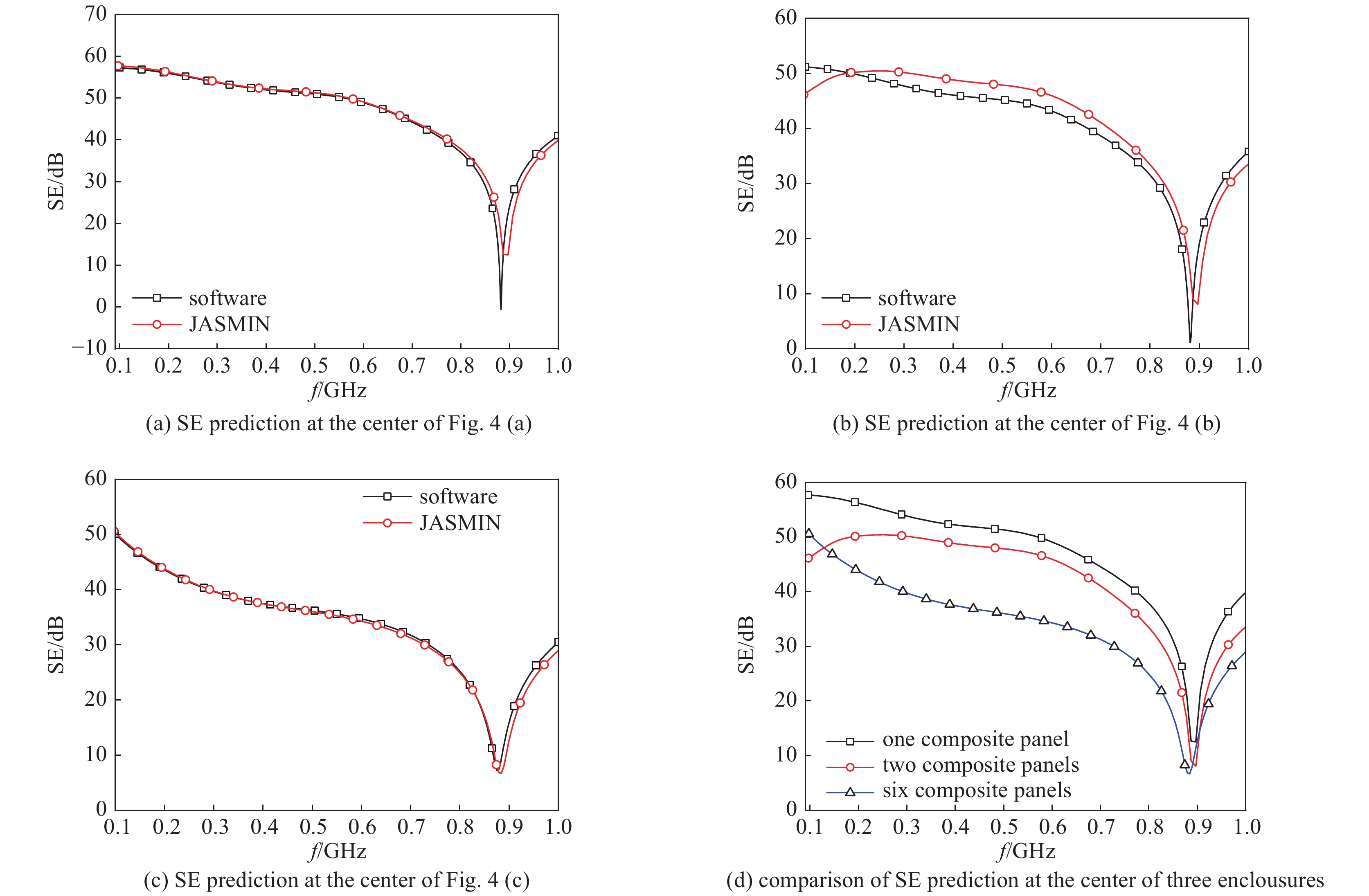
model type method total cells computation time/s model in Fig.3 nondispersive software 2.31×107 27950 SGBC-FDTD 0.64×106 1181 model in Fig.4（a） nondispersive software 1.43×107 66761 SGBC-FDTD 0.71×106 1056 dispersive software 1.23×107 19586 SGBC-FDTD 0.71×106 1467 model in Fig.4（b） nondispersive software 2.36×107 28067 SGBC-FDTD 0.71×106 1537 dispersive software 1.29×108 141281 SGBC-FDTD 0.71×106 2540 model in Fig.4（c） nondispersive software 2.31×107 31315 SGBC-FDTD 0.64×106 1523 dispersive software 1.26×108 144824 SGBC-FDTD 0.64×106 2501
下载: 导出CSV
-
[1] Wang Jianbao, Zhou Bihua, Shi Lihua, et al. Analyzing the electromagnetic performances of composite materials with the FDTD method[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(5): 2646-2654. doi: 10.1109/TAP.2013.2242824 [2] 王富强, 马晨, 王东红, 等. 屏蔽复合材料设备舱电磁脉冲屏蔽效能[J]. 强激光与粒子束, 2015, 27:103245. (Wang Fuqiang, Ma Chen, Wang Donghong, et al. Electromagnetic pulse shielding effectiveness of the conductive composites equipment compartment[J]. High Power Laser and Particle Beams, 2015, 27: 103245 doi: 10.11884/HPLPB201527.103245 [3] 孟雪松, 鲍献丰, 刘德赟, 等. 嵌入式薄片模型在时域有限差分算法中的应用[J]. 强激光与粒子束, 2017, 29:123203. (Meng Xuesong, Bao Xianfeng, Liu Deyun, et al. Embedded thin film model in finite difference time domain method[J]. High Power Laser and Particle Beams, 2017, 29: 123203 doi: 10.11884/HPLPB201729.170196 [4] 葛德彪, 闫玉波. 电磁波时域有限差分方法[M]. 3版. 西安: 西安电子科技大学出版社, 2011.Ge Debiao, Yan Yubo. Finite-difference time-domain method for electromagnetic waves[M]. 3rd ed. Xi’an: Xidian University Press, 2011 [5] Maloney J G, Smith G S. The use of surface impedance concepts in the finite-difference time-domain method[J]. IEEE Transactions on Antennas and Propagation, 1992, 40(1): 38-48. doi: 10.1109/8.123351 [6] Feliziani M, Maradei F, Tribellini G. Field analysis of penetrable conductive shields by the finite-difference time-domain method with impedance network boundary conditions (INBCs)[J]. IEEE Transactions on Electromagnetic Compatibility, 1999, 41(4): 307-319. doi: 10.1109/15.809801 [7] Sarto M S. A new model for the FDTD analysis of the shielding performances of thin composite structures[J]. IEEE Transactions on Electromagnetic Compatibility, 1999, 41(4): 298-306. doi: 10.1109/15.809798 [8] Meng Xuesong, Vukovic A, Benson T M, et al. Extended capability models for Carbon Fiber Composite (CFC) panels in the Unstructured Transmission Line Modeling (UTLM) method[J]. IEEE Transactions on Electromagnetic Compatibility, 2016, 58(3): 811-819. doi: 10.1109/TEMC.2016.2531791 [9] Cabello M R, Angulo L D, Alvarez J, et al. A hybrid Crank-Nicolson FDTD subgridding boundary condition for lossy thin-layer modeling[J]. IEEE Transactions on Microwave Theory and Techniques, 2017, 65(5): 1397-1406. doi: 10.1109/TMTT.2016.2637348 [10] Meng Xuesong. Modelling multi-scale problems in the transmission line modelling method[D]. Nottingham, U K: University of Nottingham, 2014. [11] Zhu Hui, Gao Cheng, Chen Hailin. An unconditionally stable radial point interpolation method based on Crank-Nicolson scheme[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16(99): 393-395. [12] Cabello M R, Angulo L D, Alvarez J, et al. Subgridding boundary conditions to model arbitrarily dispersive thin planar materials[J]. IEEE Transactions on Antennas and Propagation, 2018, 66(11): 6424-6434. [13] 莫则尧, 张爱清. 并行自适应结构网格应用支撑软件框架(JASMIN 2.0版)用户指南[M]. 2011.Mo Zeyao, Zhang Aiqing. User guide of J parallel adaptive structured mesh applications infrastructure (JASMIN 2.0)[Z]. 2011 [14] 张青洪, 廖成, 李瀚宇, 等. 基于JASMIN框架的抛物方程有限差分解法并行计算及其应用[J]. 强激光与粒子束, 2015, 27:083204. (Zhang Qinghong, Liao Cheng, Li Hanyu, et al. Parallel computing of finite difference algorithm for parabolic equation based on JASMIN and its application[J]. High Power Laser and Particle Beams, 2015, 27: 083204 doi: 10.11884/HPLPB201527.083204 [15] 李俊辛, 刘强, 闫丽萍, 等. 基于JASMIN的并行CP-FDTD建模与屏蔽效能评估应用[J]. 强激光与粒子束, 2019, 31:053202. (Li Junxin, Liu Qiang, Yan Liping, et al. JASMIN-based parallel CP-FDTD modeling and application to shielding effectiveness prediction[J]. High Power Laser and Particle Beams, 2019, 31: 053202 doi: 10.11884/HPLPB201931.190026 [16] Gustavsen B, Semlyen A. Rational approximation of frequency domain responses by vector fitting[J]. IEEE Transactions on Power Delivery, 1999, 14(3): 1052-1061. doi: 10.1109/61.772353 [17] 方明江, 刘强, 闫丽萍, 等. 含三维复杂工程细缝金属腔的电磁屏蔽效能评估[J]. 强激光与粒子束, 2018, 30:073201. (Fang Mingjiang, Liu Qiang, Yan Liping, et al. Evaluation of electromagnetic shielding effectiveness for metallic enclosure with three-dimensional complex thin slots[J]. High Power Laser and Particle Beams, 2018, 30: 073201 doi: 10.11884/HPLPB201830.180047 [18] Elmahgoub K, Elsherbeni A Z, Yang Fan. Dispersive periodic boundary conditions for finite-difference time-domain method[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(4): 2118-2122. doi: 10.1109/TAP.2012.2186243 -
点击查看大图
计量
- 文章访问数: 823
- HTML全文浏览量: 225
- PDF下载量: 38
- 被引次数: 0
