Progress on mode field distribution and characterization technology of the optical fiber laser
-
摘要:
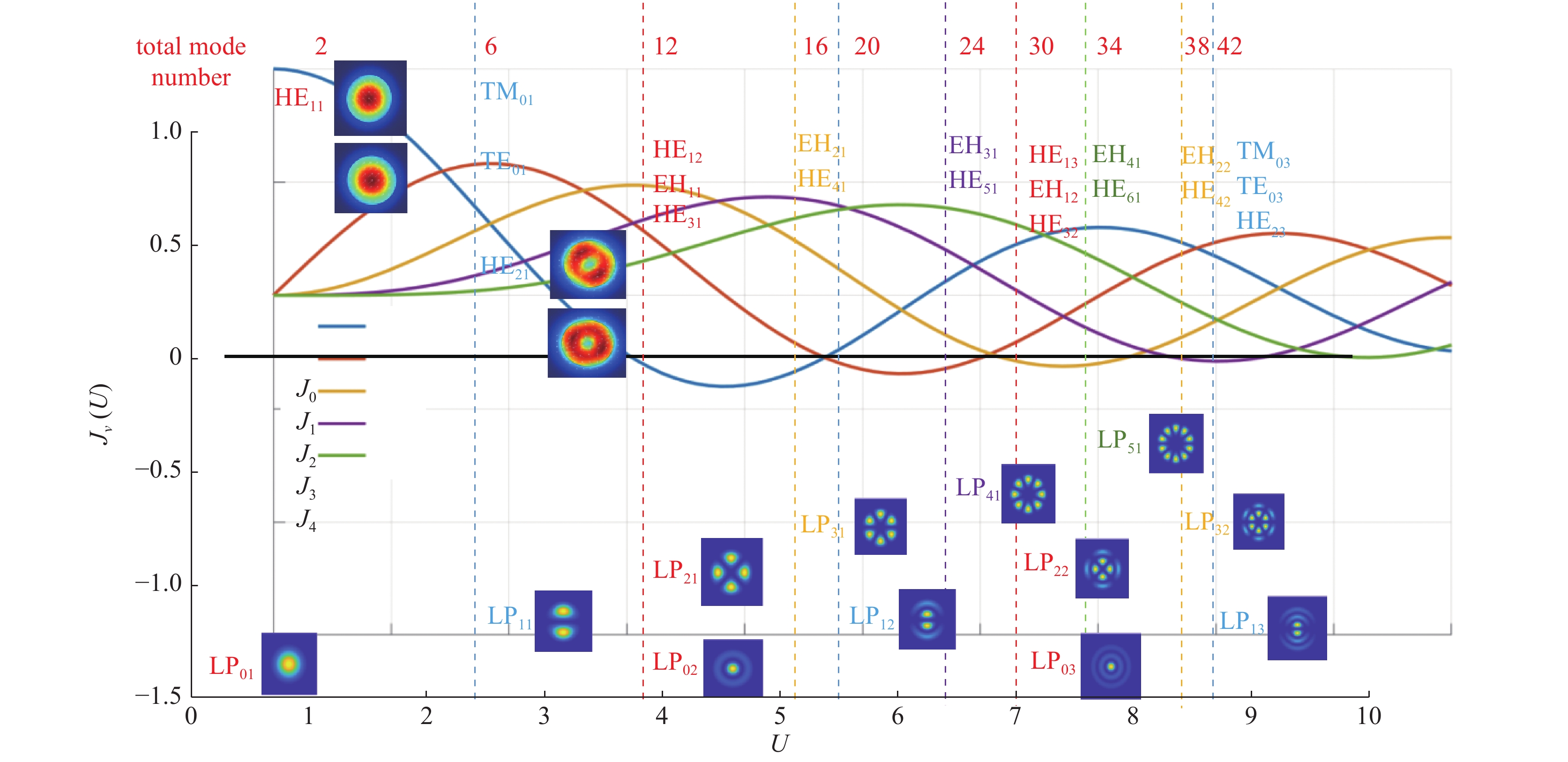
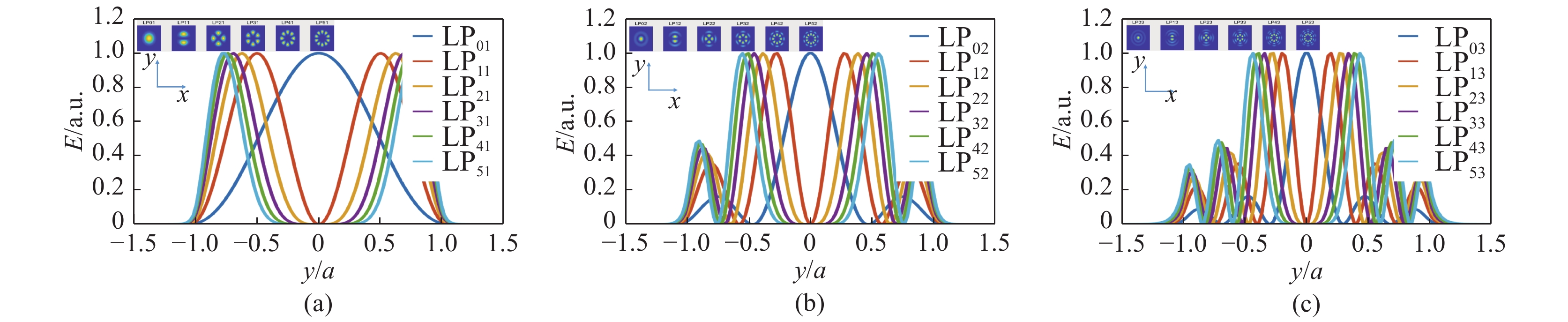
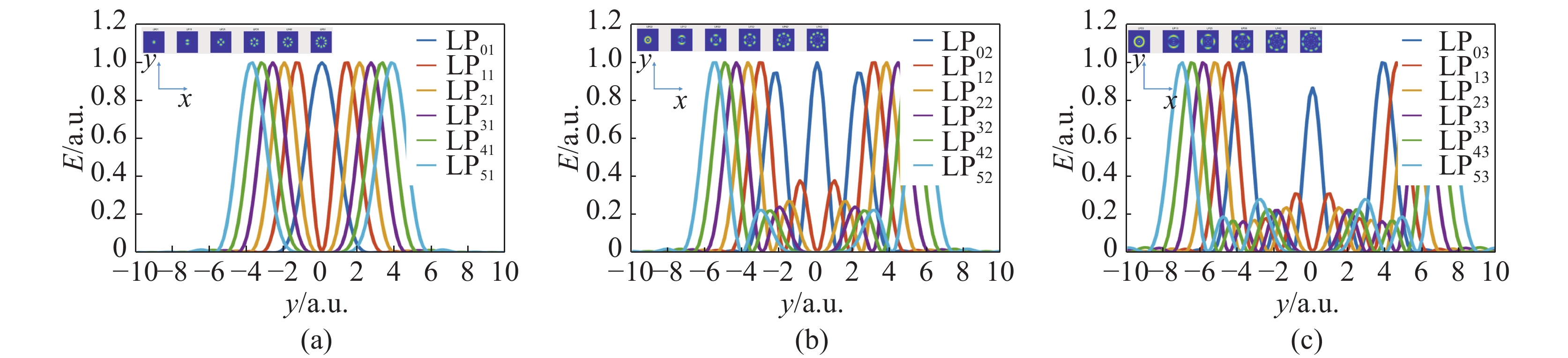
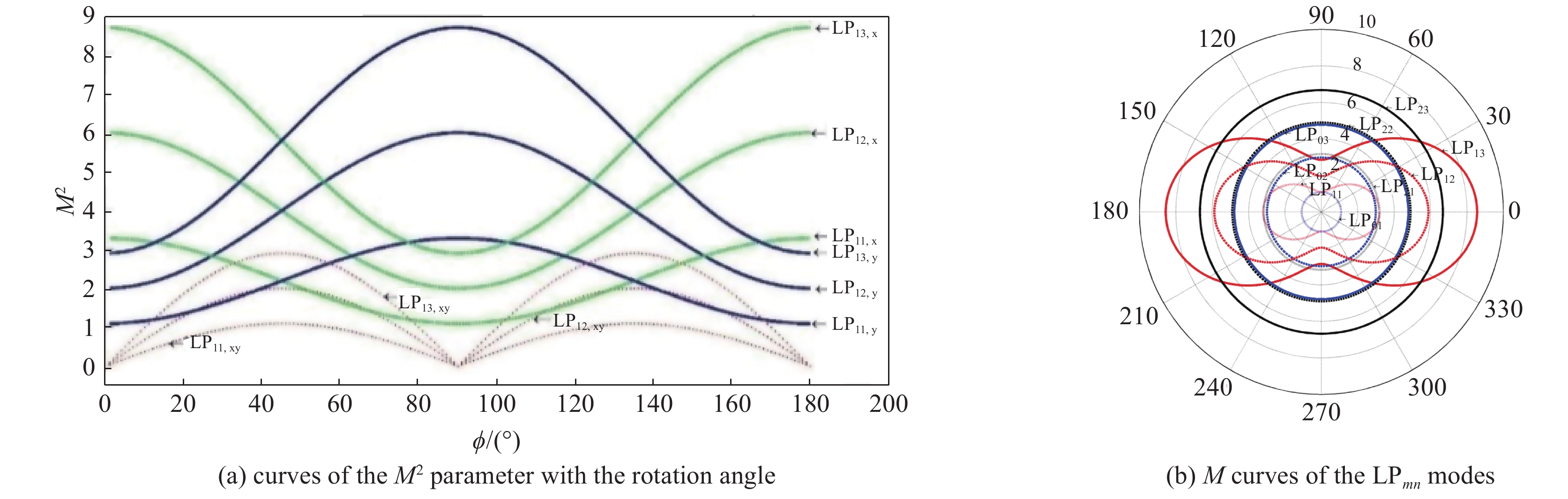
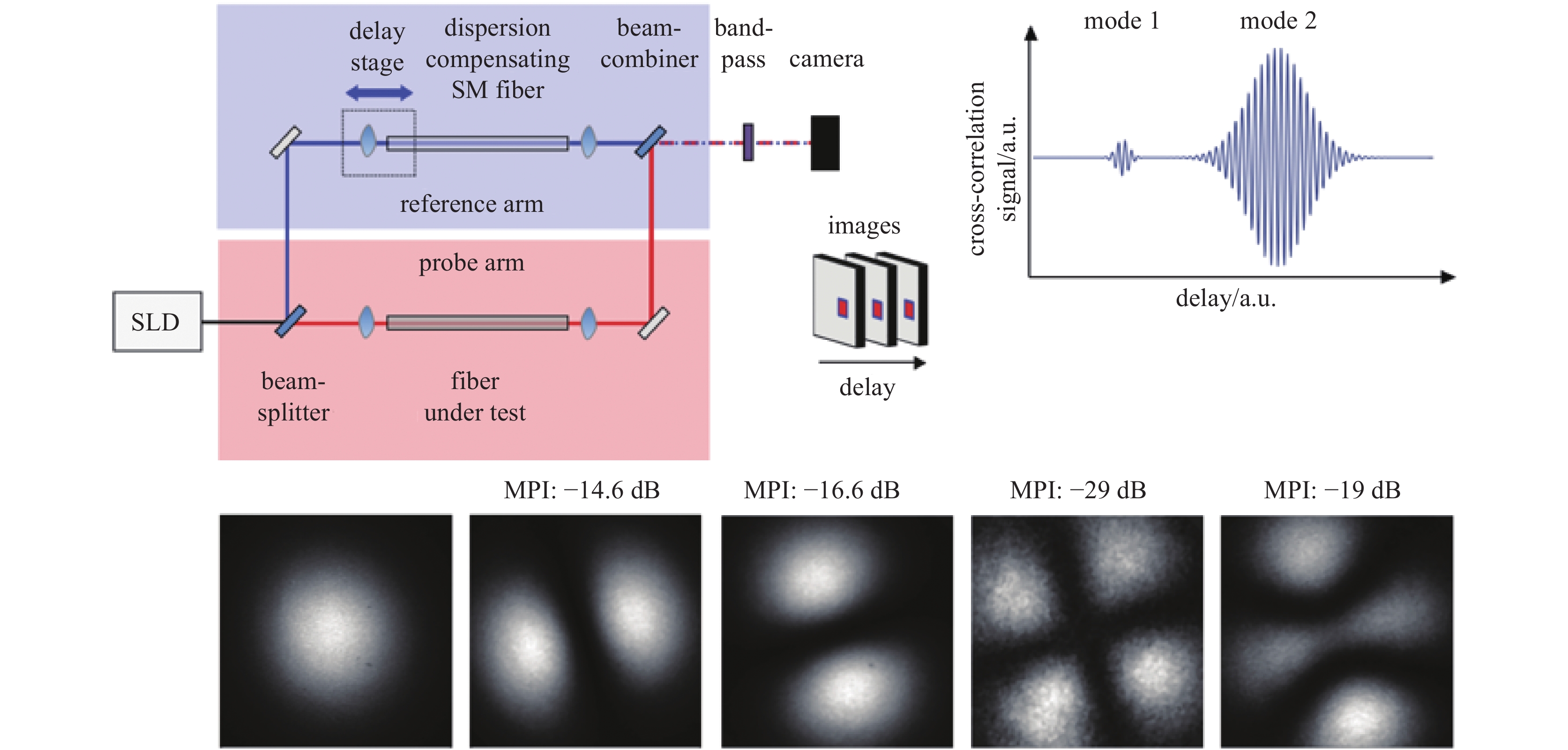
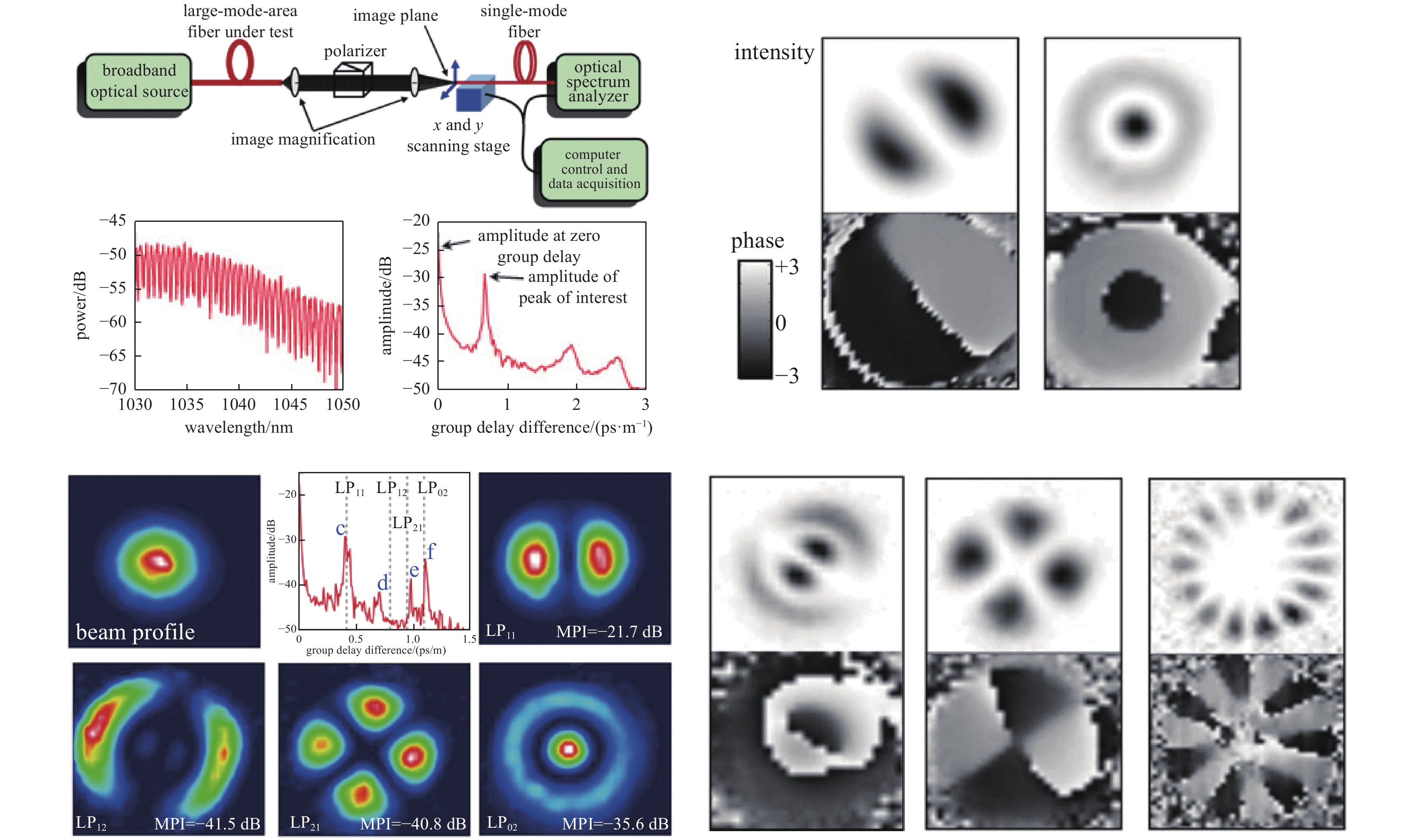
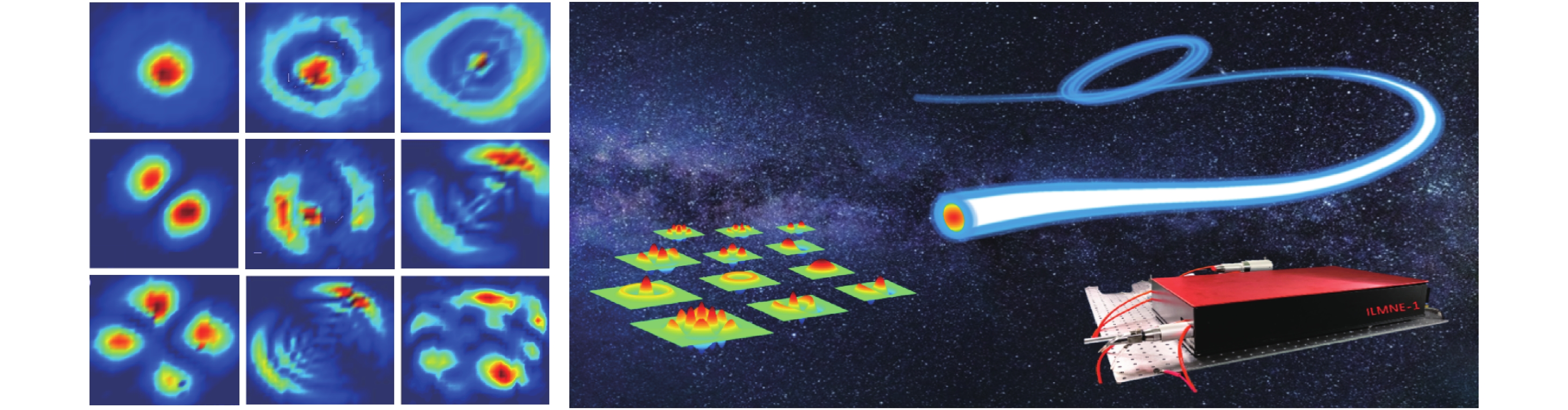
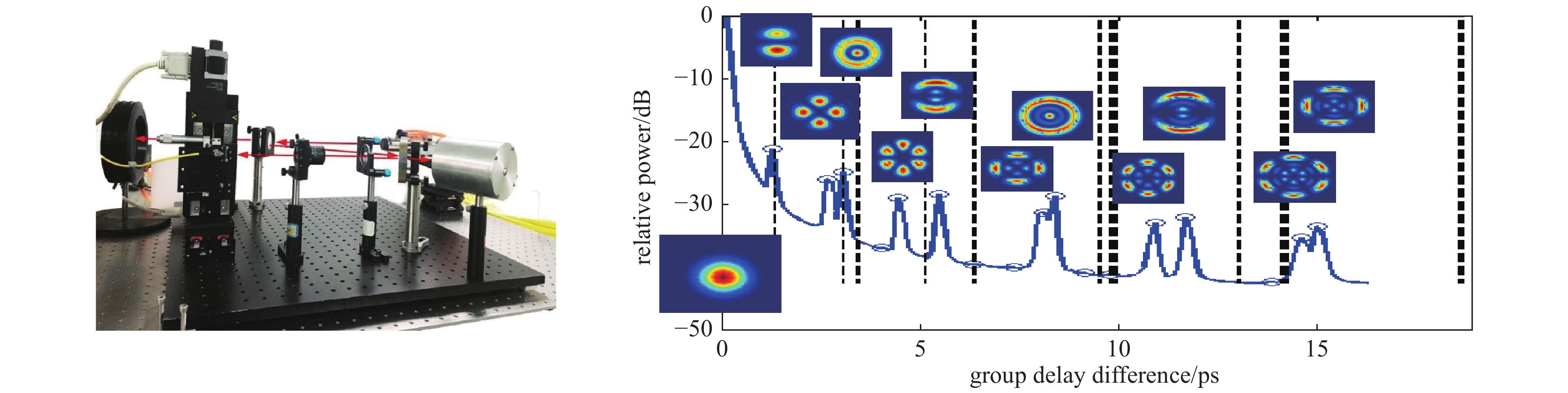
在光纤通信、光纤激光器和光纤传感等领域的实际应用中,需要重点关注光纤中的模式问题。模分复用是提高光通信信息容量的有效方法,模间干涉是大多数光纤传感的基本方法,高功率光纤激光的光束质量控制的关键技术之一就是模式控制,因此,对光纤模式理论、模式产生及转换、模式表征技术开展研究具有重要的研究意义和实际应用价值。论文讨论了光纤的模式及光束质量,分析了多种模式发生及转换的方法,将模式表征方法归结为非相干、相干和低相干测量法。光纤模式表征是目前的研究热点,在多种表征方法中,空间和频谱成像法(S2)和双重傅里叶变换法(F2)具有显著的优越性,可不需要提前知道光纤的几何参数,就可获得模场分布、模式功率占比、群时延等特性。研究表明F2法更适合于表征高功率光纤激光的模场特性。
Abstract:In fields of practical applications such as the optical fiber communications, optical fiber lasers, and optical fiber sensinIn fields of practical applications such as the optical fiber communication, the optical fiber laser, and the optical fiber sensing, it is necessary to focus on the mode problems in optical fibers. Mode division multiplexing is an effective method to improve the information capacity of optical communication. Interference between modes is the basic method for the most of optical fiber sensing. Mode controlling technique is one of the key technologies for beam quality control of high-power fiber lasers. Therefore, research on the theory of optical fiber modes, modes’ generation, modes’ conversion, and mode characterization technology are of great significance and practical application value. In this paper, we discuss the mode and beam quality of the optical fiber, analyze the methods of multiple modes’ generation and conversion, and summarize the mode characterization methods by means of incoherent, coherent and low-coherence measurement. Currently, the fiber mode characterization is a hot research topic. Among a variety of characterization methods, the spatial and spectral imaging method (S2) and the spatial and spectral double Fourier transform method (F2) have significant advantages. Without knowing the geometric parameters of the fiber in advance, we can obtain characteristics such as the mode field distribution, the mode power ratio, and the group time delay. Results indicate that the F2 method is better for characterizing mode field distributions of high-power fiber lasers.
-
-
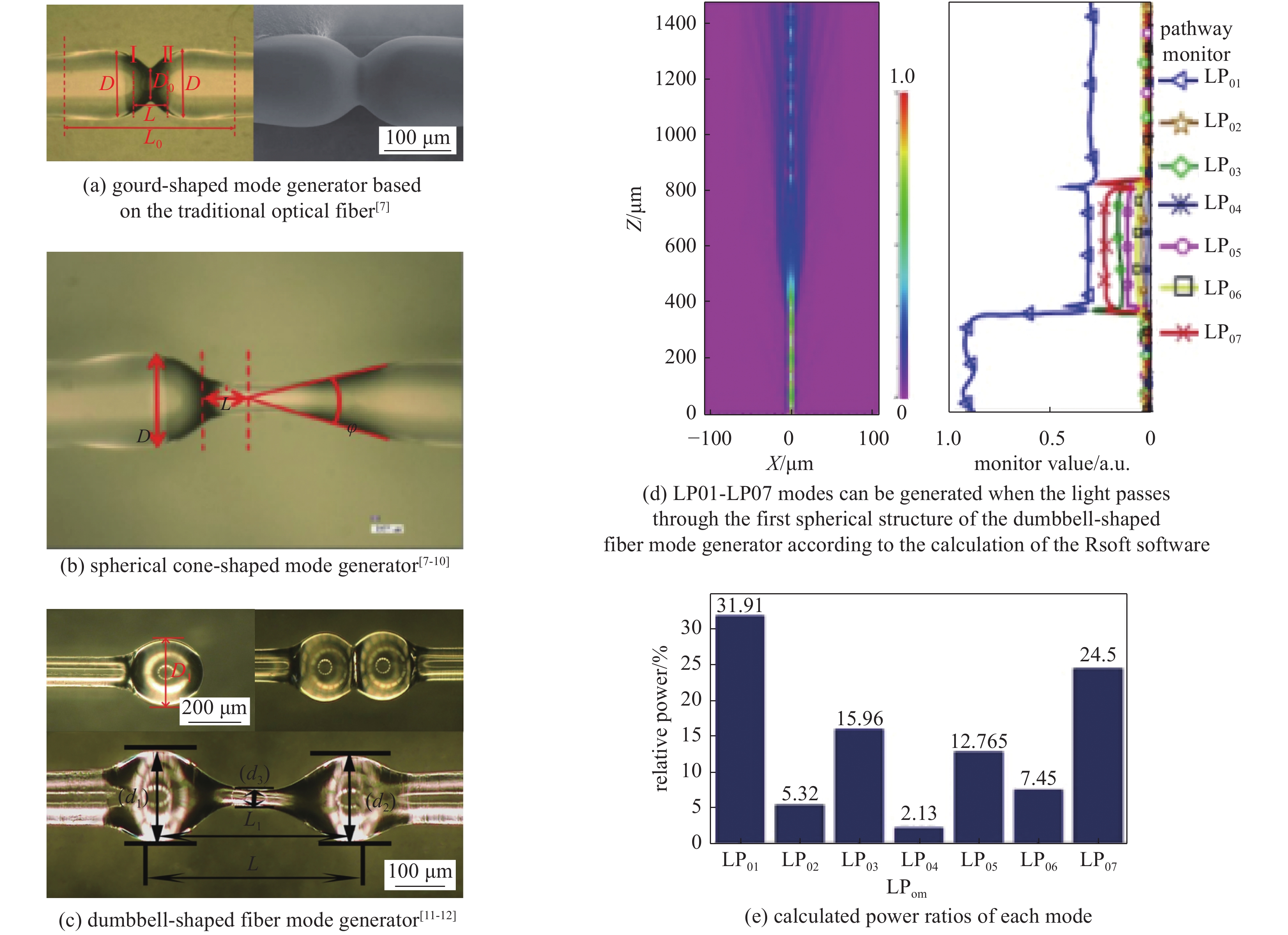
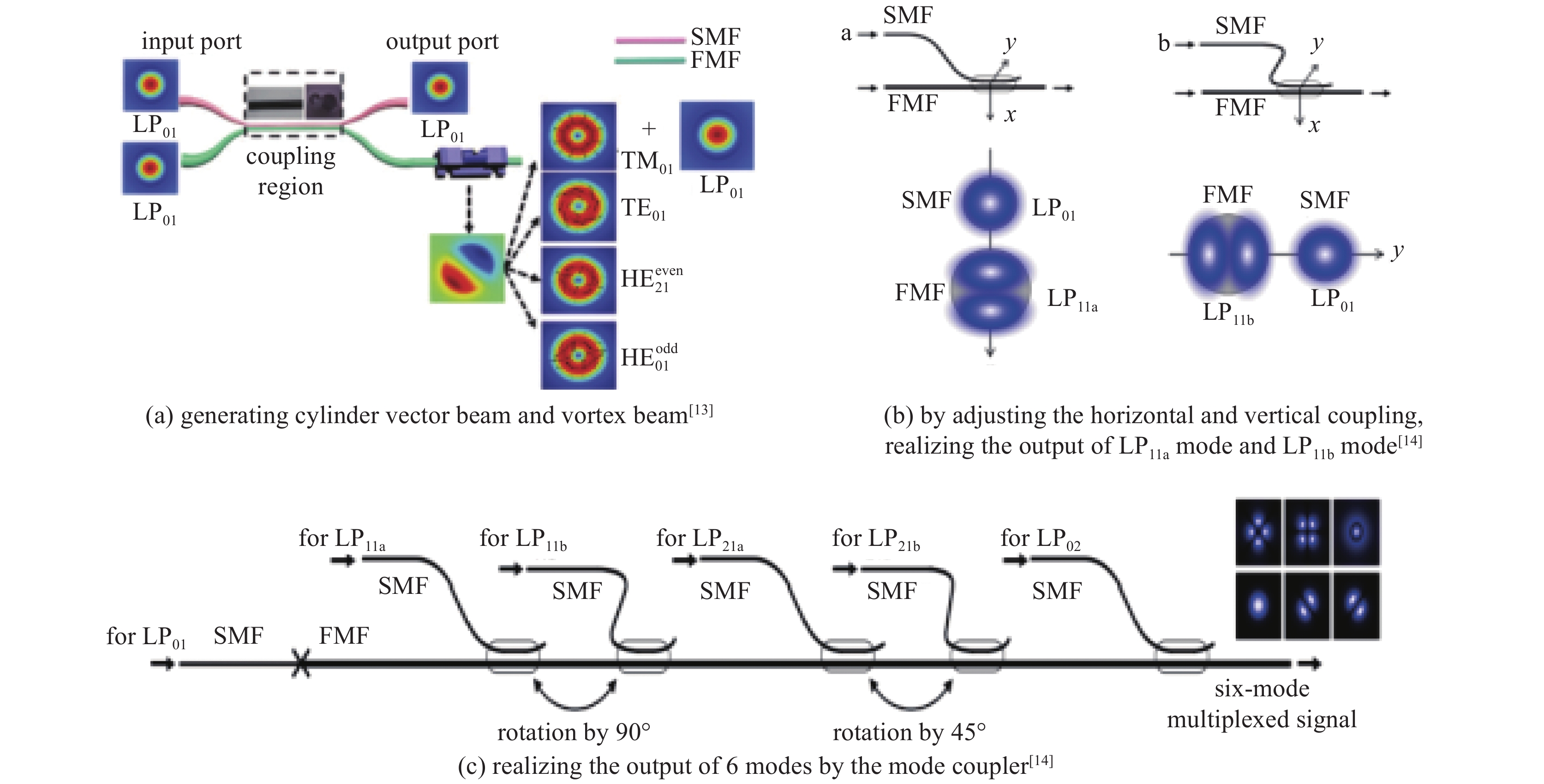
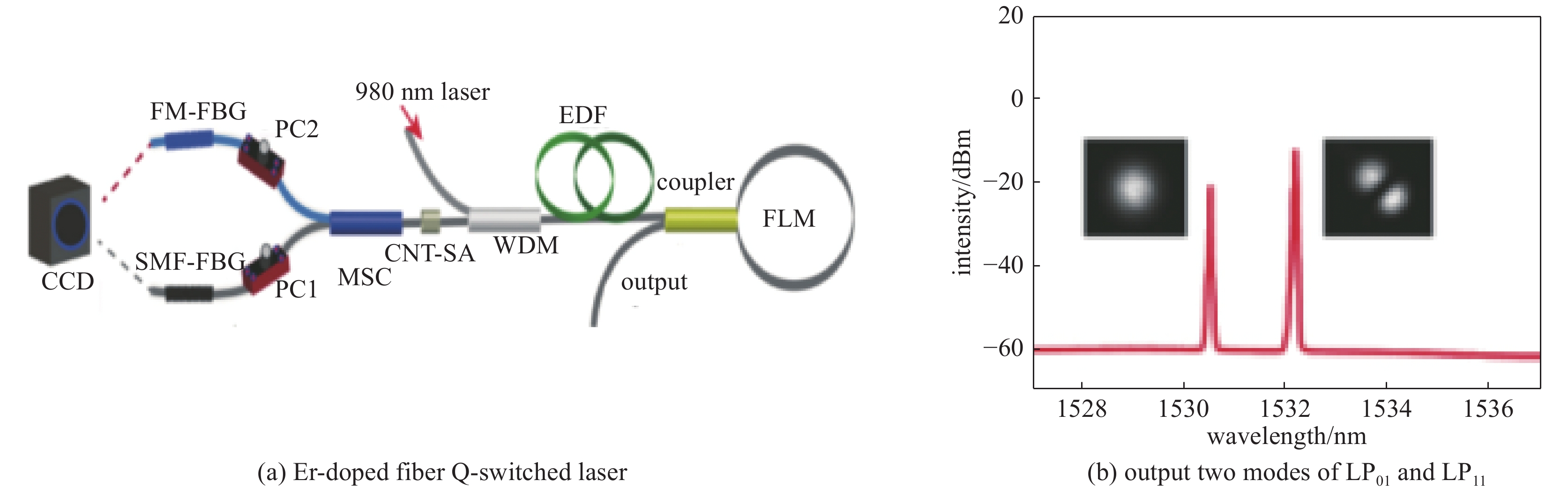
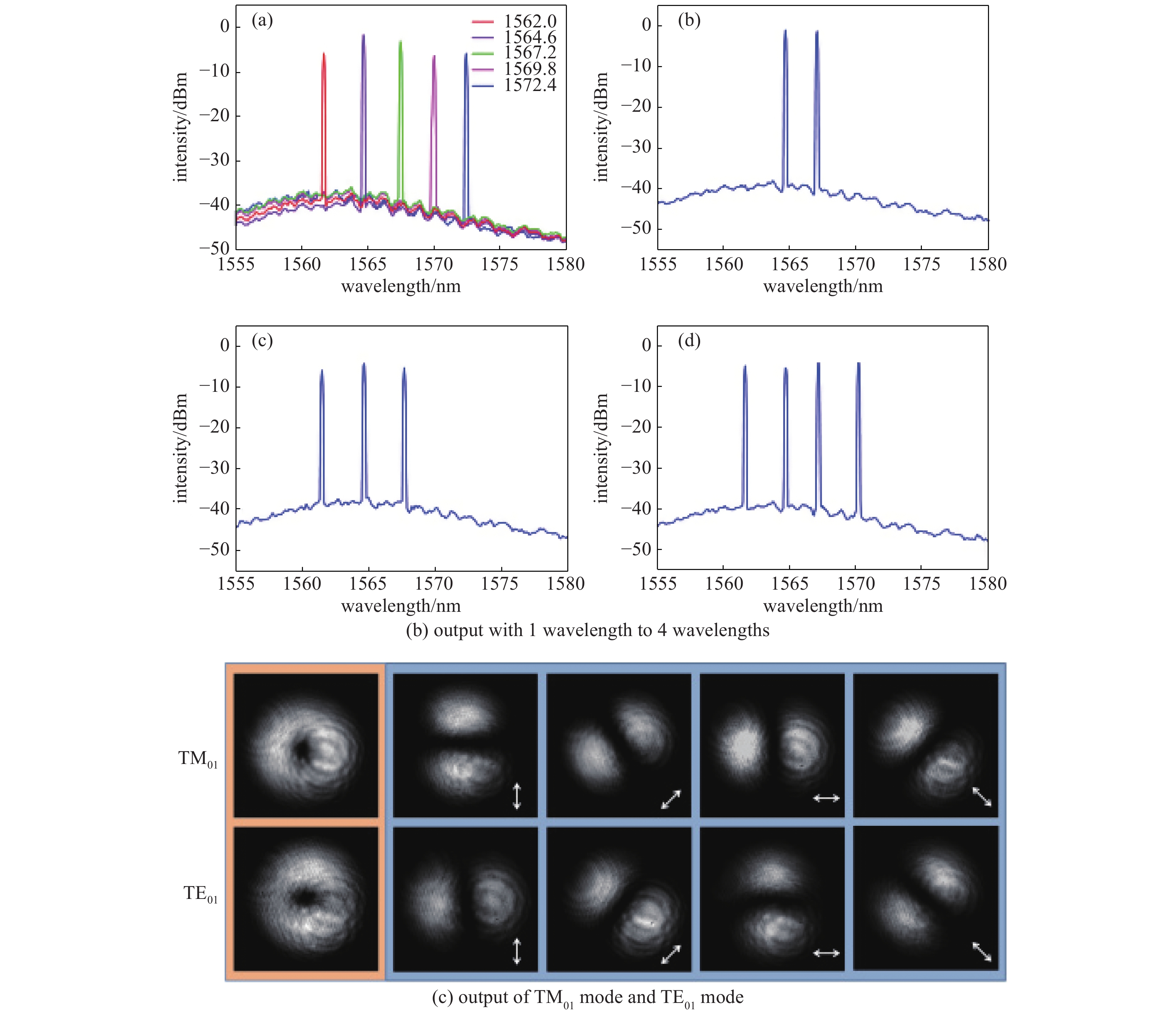
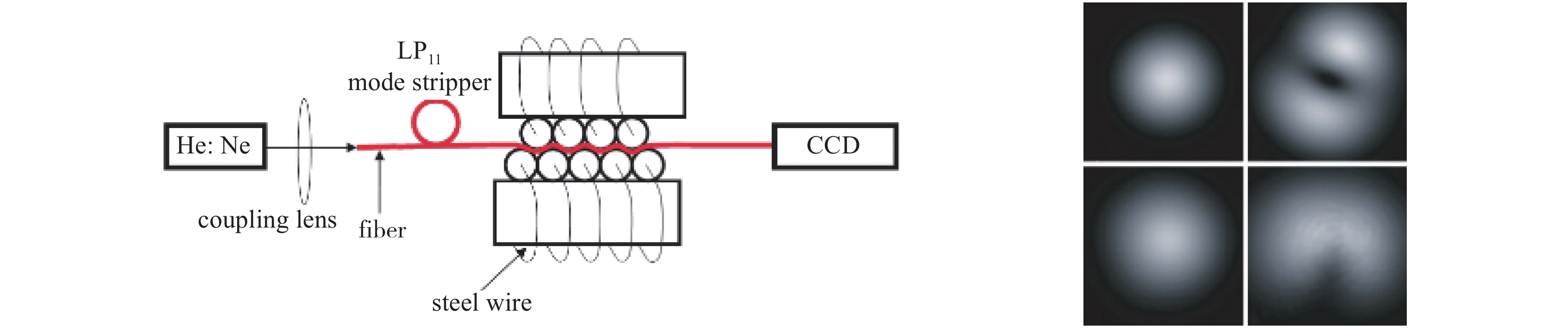
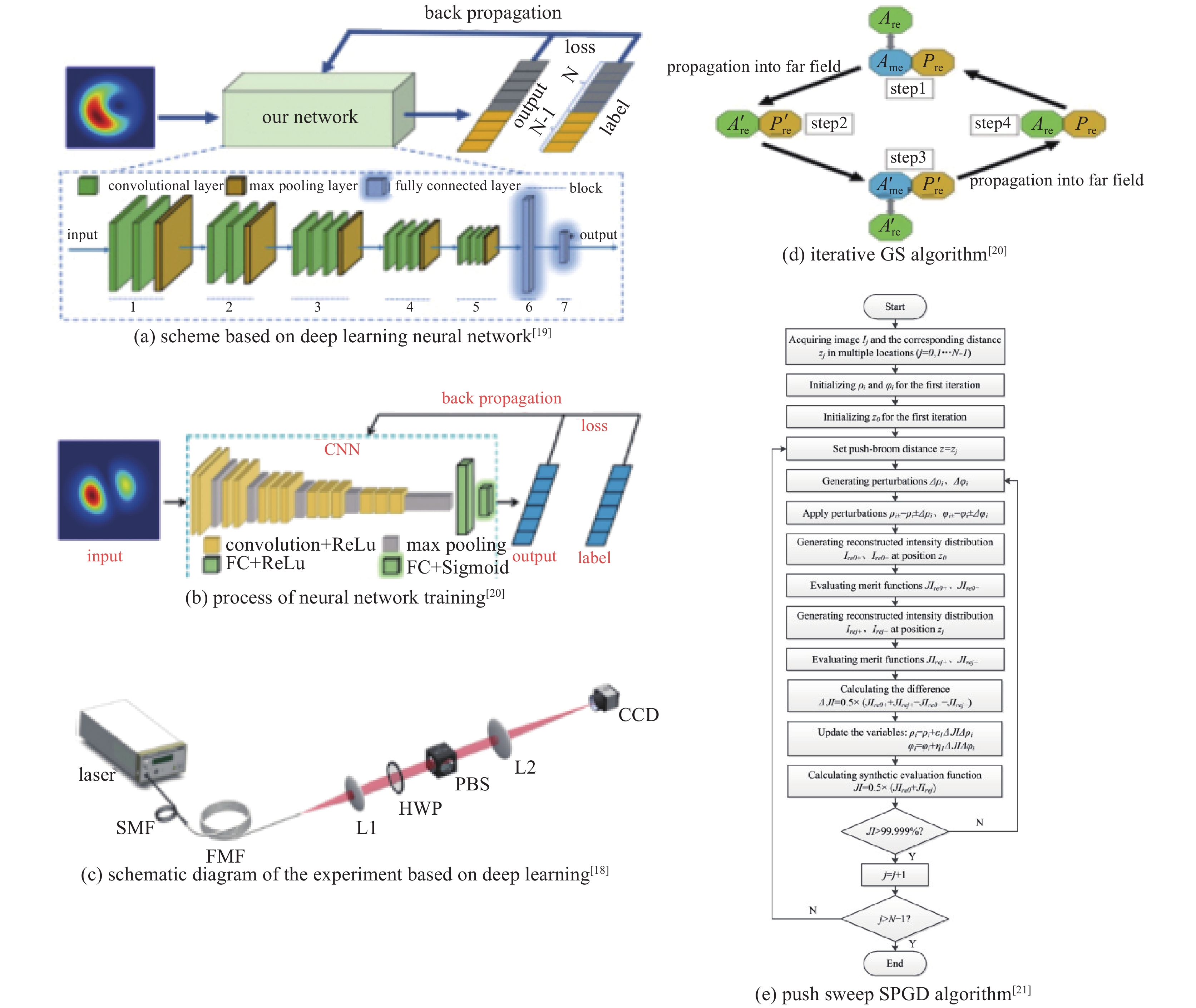
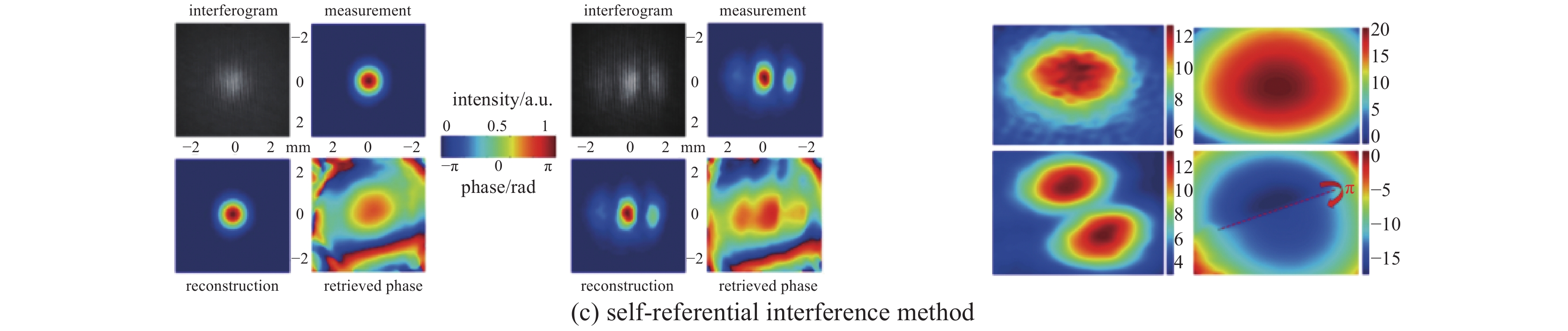
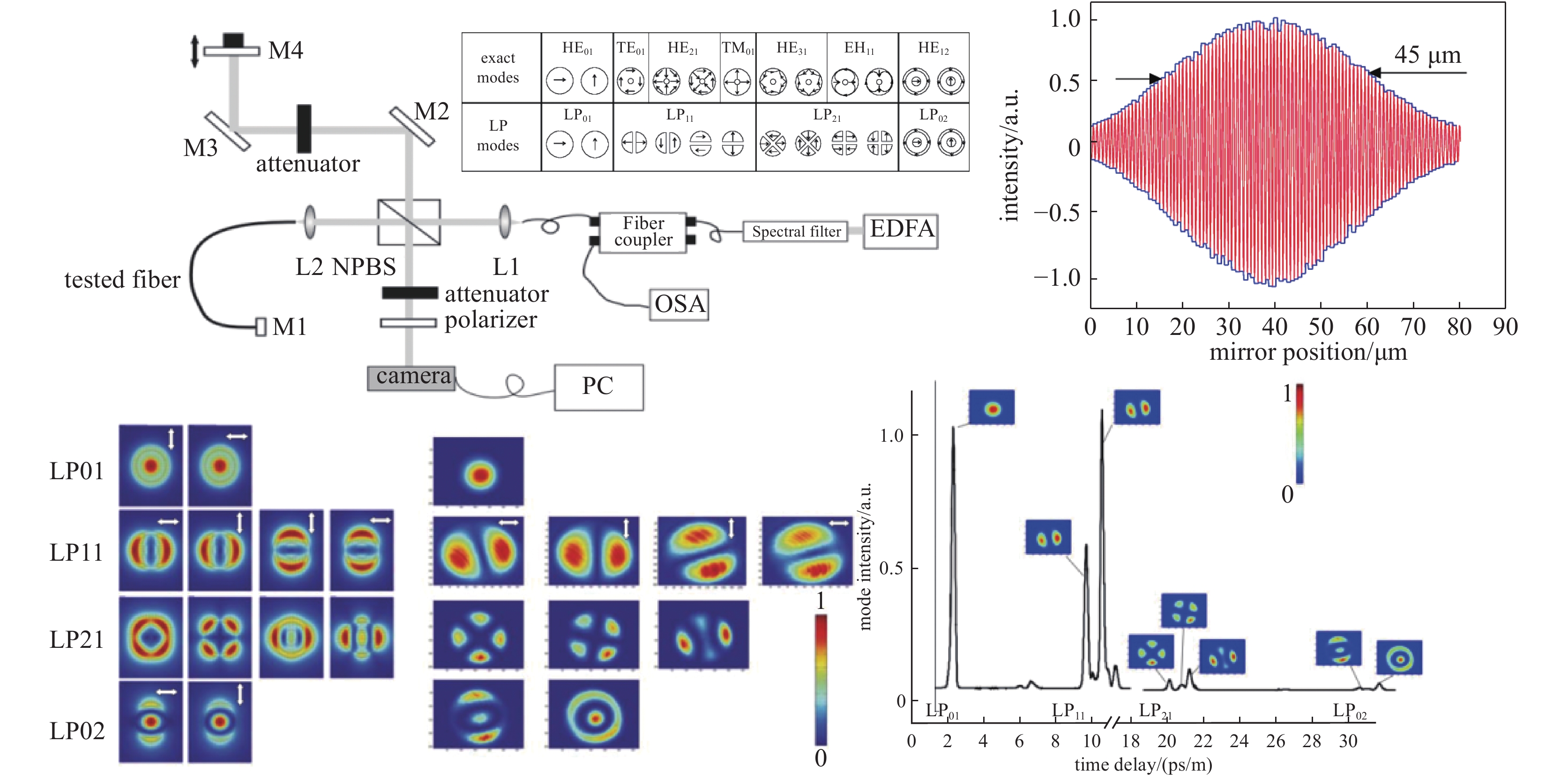
[1] Kao K C, Hockham G A. Dielectric-fibre surface waveguides for optical frequencies[J]. IEE Proceedings, 1986, 133(3): 191-198. [2] Yoda H, Polynkin P, Mansuripur M. Beam quality factor of higher order modes in a step-index fiber[J]. Journal of Lightwave Technology, 2006, 24(3): 1350-1355. doi: 10.1109/JLT.2005.863337 [3] Wielandy S. Implications of higher-order mode content in large mode area fibers with good beam quality[J]. Optical Express, 2007, 15(23): 15402-15409. doi: 10.1364/OE.15.015402 [4] Fu Yuqing, Feng Guoying, Zhang Dayong, et al. Beam quality factor of mixed modes emerging from a multimode step-index fiber[J]. Optik, 2010, 121(5): 452-456. doi: 10.1016/j.ijleo.2008.08.003 [5] 冯国英, 周寿桓, 高春清. 激光模场及光束质量表征[M]. 北京: 国防工业出版社, 2016.Feng Guoying, Zhou Shouhuan, Gao Chunqing. Laser mode field and beam quality characterization[M]. Beijing: National Defense Industry Press, 2016 [6] 冯国英, 周寿桓. 激光束的强度矩描述[M]. 北京: 国防工业出版社, 2016.Feng Guoying, Zhou Shouhuan, Gao Chunqing. Characterization of intensity moment of laser beam[M]. Beijing: National Defense Industry Press, 2016. [7] Xian Pei, Feng Guoying, Zhou Shouhuan. A compact and stable temperature sensor based on a gourd-shaped microfiber[J]. IEEE Photonics Technology Letters, 2016, 28(1): 95-98. doi: 10.1109/LPT.2015.2487281 [8] Xian Pei, Feng Guoying, Ju Yao, et al. Single-mode all-fiber structured modal interference for temperature and refractive index sensing[J]. Laser Physics Letters, 2017, 14: 085101. doi: 10.1088/1612-202X/aa779c [9] Xian Pei, Feng Guoying, Zhou Shouhuan. A microsphere-taper cascading structured microfiber for temperature sensing[C]//Proc of SPIE. 2016: 98861H. [10] Xian Pei, Feng Guoying, Dai Shenyu, et al. Asymmetric structured microfiber-based temperature sensor[J]. Optical Engineering, 2017, 56: 047106. doi: 10.1117/1.OE.56.4.047106 [11] Tan Jianchang, Feng Guoying, Liang Jingchuan, et al. Optical fiber temperature sensor based on dumbbell-shaped Mach–Zehnder interferometer[J]. Optical Engineering, 2018, 57: 017112. [12] Tan Jianchang, Feng Guoying, Zhang Shulin, et al. Dual spherical single-mode-multimode-single-mode optical fiber temperature sensor based on a Mach-Zehnder interferometer[J]. Laser Physics, 2018, 28: 075102. doi: 10.1088/1555-6611/aabb26 [13] Yao Han, Shi Fan, Wu Zhaoyang, et al. A mode generator and multiplexer at visible wavelength based on all-fiber mode selective coupler[J]. Nanophotonics, 2020, 9(4): 973-981. doi: 10.1515/nanoph-2020-0050 [14] Igarashi K, Park K J, Tsuritani T, et al. All-fiber-based selective mode multiplexer and demultiplexer for weakly-coupled mode-division multiplexed systems[J]. Optics Communications, 2018, 408: 58-62. doi: 10.1016/j.optcom.2017.08.049 [15] 程培康, 石帆, 王腾, 等. 基于模式选择耦合器的光纤模式可切换调Q激光器[J]. 中国激光, 2020, 47:1201001. (Cheng Peikang, Shi Fan, Wang Teng, et al. Fiber mode switchable Q-switched laser based on mode selective coupler[J]. Chinese Journal of Lasers, 2020, 47: 1201001 doi: 10.3788/CJL202047.1201001 [16] Wang Teng, Yang Ao, Shi Fan, et al. High-order mode lasing in all-FMF laser cavities[J]. Photonics Research, 2018, 7(1): 42-49. [17] Skorobogatiy M, Anastassiou C, Johnson S G, et al. Quantitative characterization of higher-order mode converters in weakly multimoded fibers[J]. Optics Express, 2003, 11(22): 2838-2847. doi: 10.1364/OE.11.002838 [18] An Yi, Huang Liangjin, Li Jun, et al. Learning to decompose the modes in few-mode fibers with deep convolutional neural network[J]. Optics Express, 2019, 27(7): 10127-10137. doi: 10.1364/OE.27.010127 [19] An Yi, Huang Liangjin, Li Jun, et al. Deep learning-based real-time mode decomposition for multimode fibers[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2020, 26: 4400806. [20] An Yi, Huang Liangjin, Li Lei, et al. Numerical mode decomposition for multimode fiber: from multi-variable optimization to deep learning[J]. Optical Fiber Technology, 2019, 52: 101960. doi: 10.1016/j.yofte.2019.101960 [21] Chen Fan, Zhao Shubin, Wang Qiang, et al. Modal decomposition of a fibre laser beam based on the push-broom stochastic parallel gradient descent algorithm[J]. Optics Communications, 2021, 481: 126538. doi: 10.1016/j.optcom.2020.126538 [22] Kaiser T, Flamm D, Schröter S, et al. Complete modal decomposition for optical fibers using CGH-based correlation filters[J]. Optics Express, 2009, 17(11): 9347-9356. doi: 10.1364/OE.17.009347 [23] Andermahr N, Theeg T, Fallnich C. Novel approach for polarization-sensitive measurements of transverse modes in few-mode optical fibers[J]. Applied Physics B, 2008, 91(2): 353-357. doi: 10.1007/s00340-008-3011-9 [24] Ma Yuzhao, Sych Y, Onishchukov G, et al. Fiber-modes and fiber-anisotropy characterization using low-coherence interferometry[J]. Applied Physics B, 2009, 96(2/3): 345-353. [25] Schimpf D N, Barankov R A, Ramachandran S. Cross-correlated (C2) imaging of fiber and waveguide modes[J]. Optics Express, 2011, 19(14): 13008-13019. doi: 10.1364/OE.19.013008 [26] Yan Cheng, Huang Sujuan, Yin Weihao, et al. Modal content analysis of optical fiber based on cross-correlated and off-axis digital holography[J]. Optical Fiber Technology, 2021, 62: 102475. doi: 10.1016/j.yofte.2021.102475 [27] Nicholson J W, Yablon Y D, Ramachandran S, et al. Spatially and spectrally resolved imaging of modal content in large-mode-area fibers[J]. Optics Express, 2008, 16(10): 7233-7243. doi: 10.1364/OE.16.007233 [28] Nicholson J W, Yablon A D, Fini J M, et al. Measuring the modal content of large-mode-area fibers[J]. IEEE Journal of Selected Topics in Quantum Electronics, 2009, 15(1): 61-70. doi: 10.1109/JSTQE.2008.2010239 [29] Nguyen D M, Blin S, Nguyen T N, et al. Modal decomposition technique for multimode fibers[J]. Applied Optics, 2012, 51(4): 450-456. doi: 10.1364/AO.51.000450 [30] 张澍霖, 冯国英, 周寿桓. 基于空间域和频率域傅里叶变换F2的光纤模式成分分析[J]. 物理学报, 2016, 65:154202. (Zhang Shulin, Feng Guoying, Zhou Shouhuan. Fiber modal content analysis based on spatial and spectral Fourier transform[J]. Acta Physica Sinica, 2016, 65: 154202 doi: 10.7498/aps.65.154202 期刊类型引用(3)
1. 李醒飞,何梦洁,拓卫晓,王天宇,韩佳欣,王信用. 应用于运动平台光电跟瞄系统的惯性参考单元研究综述. 光学精密工程. 2024(03): 401-421 .  百度学术
百度学术2. 冯志刚,王鹏. 交通执法光电跟踪系统设计与实现. 传感技术学报. 2024(06): 1090-1098 .  百度学术
百度学术3. 周占民,李贤涛,毛大鹏,张保. 永磁同步电机驱动的小型三轴机载光电平台鲁棒控制系统设计. 国外电子测量技术. 2023(05): 119-124 .  百度学术
百度学术其他类型引用(3)
-





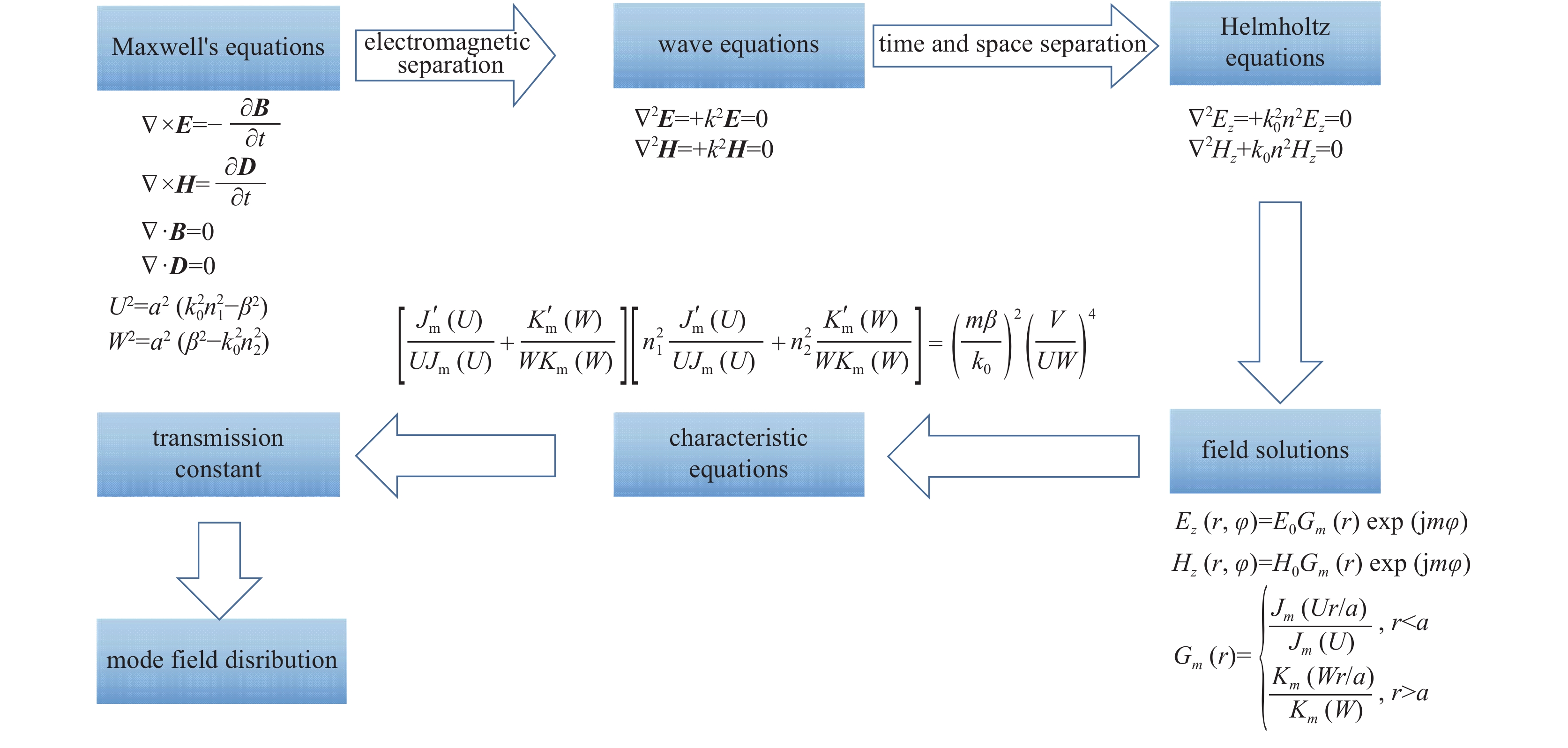
 下载:
下载: