Self-consistent nonlinear numerical simulation of millimeter wave gyro-klystron amplifiers
-
摘要: 为了实现回旋速调管放大器的快速设计，基于经典的回旋管的稳态单模非线性理论方法，开展了回旋速调管放大器的束波作用效率的理论模拟研究。由于单模理论无法匹配回旋速调管放大器的输入腔、中间腔两端的突变边界条件，所以输入腔与中间腔都只能采用给定场法进行求解。回旋速调管的输出腔的功率输出端通常采用缓变结构，这种腔体可以采用单模自洽理论进行求解。对两腔毫米波回旋速调管放大器进行了理论模拟，并与商业粒子模拟软件的结果进行对比，验证了该数值理论模拟方法的有效性。Abstract: To realize quick design of the gyro-klystron amplifiers, a kind of numerical simulation method based on the single mode self-consistent nonlinear theory of gyrotrons was investigated. The single mode theory can’t be used to match the disrupt boundary conditions of the input and the middle cavities of the gyro-klystrons, thus the input and the middle cavities can only be processed through single mode theory based on given field distributions. As for the output cavities with smooth boundaries at the power output ends, the single mode nonlinear simulation could be self-consistent. A millimeter wave two cavity gyro-klystron amplifier with reported detailed parameters was simulated using the developed single mode theory. The effectiveness of the numerical simulation was verified by comparing the simulation results with those obtained in a commercial particle in cell (PIC) simulation tool.
-
图 2 Ka波段两腔二次谐波回旋速调管放大器PIC模型
Figure 2. PIC model of a Ka band two cavity second harmonic gyro-klystron amplifier
图 3 Ka波段两腔二次谐波回旋速调管放大器输入腔内的电子效率
Figure 3. Electronic efficiency in input cavity of the Ka band two cavity second harmonic gyro-klystron amplifier
图 4 Ka波段两腔二次谐波回旋速调管放大器不同位置处的电子相空间图
Figure 4. Electron phase space at different stage of the Ka band two cavity second harmonic gyro-klystron amplifier
表 1 Ka波段两腔二次谐波回旋速调管放大器参数
Table 1. Parameters of a Ka band two cavity second harmonic gyro-klystron amplifier
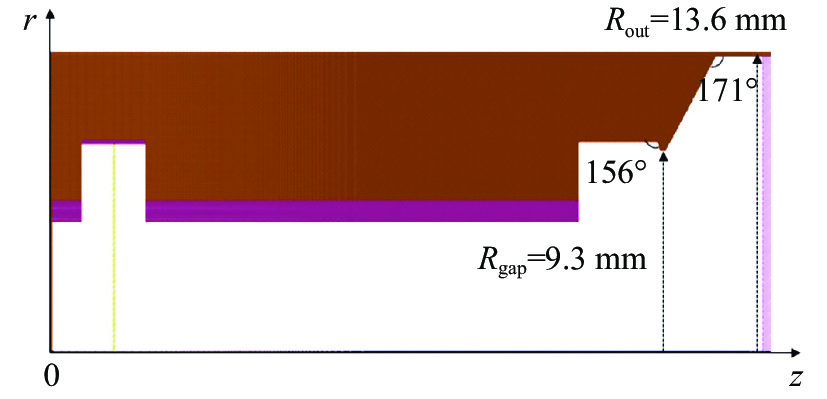
stage radius/mm length/mm Q frequency/GHz input 9.77 20.6 300 35.0 output 9.66 25.3 610 34.96 drift 7.0 122 
下载: 导出CSV
-
[1] Danly B G, Blank M, Calame J P, et al. Development and testing of a high-average power, 94-GHz gyroklystron[J]. IEEE Transactions on Plasma Science, 2000, 28(3): 713-726. doi: 10.1109/27.887710 [2] 罗勇. 回旋速调放大器高频系统及注-波互作用研究[D]. 成都: 电子科技大学, 2003Luo Yong. High frequency system and beam-wave interaction study of gyro-klystron amplifiers[D]. Chengdu: University of Electronic Science and Technology of China, 2003 [3] 罗勇, 李宏福. 回旋速调管放大器注-波互作用分析[J]. 强激光与粒子束, 2005, 17(5):724-728. (Luo Yong, Li Hongfu. Study on the interaction between electron beam and waves in gyroklystron amplifiers[J]. High Power Laser and Particle Beams, 2005, 17(5): 724-728 [4] Chu K R. The electron cyclotron maser[J]. Reviews of Modern Physics, 2004, 76(2): 489-540. doi: 10.1103/RevModPhys.76.489 [5] Levush B, Blank M, Calame J, et al. Modeling and design of millimeter wave gyroklystrons[J]. Physics of Plasmas, 1999, 6(5): 2233-2240. doi: 10.1063/1.873476 [6] Latham P E, Lawson W, Irwin V. The design of a 100 mw, Ku band second harmonic gyroklystron experiment[J]. IEEE Transactions on Plasma Science, 1994, 22(5): 804-817. doi: 10.1109/27.338296 [7] Vlasov A N, Antonsen T M, Jr Chernin D P, et al. Simulation of microwave devices with external cavities using MAGY[J]. IEEE Transactions on Plasma Science, 2002, 30(3): 1277-1291. [8] 马俊建, 朱小芳, 金晓林, 等. 回旋速调管放大器时域非线性理论与模拟[J]. 物理学报, 2012, 61:208402. (Ma Junjian, Zhu Xiaofang, Jin Xiaolin, et al. A time-dependent nonlinear theory and simulation for gyroklystron amplifier[J]. Acta Physica Sinica, 2012, 61: 208402 doi: 10.7498/aps.61.208402 [9] Fliflet A W, Read M E, Chu K R, et al. A self-consistent field theory for gyrotron oscillators: application to a low Q gyromonotron[J]. International Journal of Electronics, 1982, 53(6): 505-521. doi: 10.1080/00207218208901545 [10] 刘迎辉, 李宏福, 雷朝军, 等. 输入腔高频场的矩阵分析[J]. 强激光与粒子束, 2007, 19(6):931-933. (Liu Yinghui, Li Hongfu, Lei Chaojun, et al. Analysis of RF field in an input cavity by parameter matrix[J]. High Power Laser and Particle Beams, 2007, 19(6): 931-933 [11] 耿志辉, 刘濮鲲. 回旋速调管放大器输出腔的特性研究[J]. 强激光与粒子束, 2004, 16(11):1445-1448. (Geng Zhihui, Liu Pukun. Characteristic study of output cavity in gyroklystron amplifier[J]. High Power Laser and Particle Beams, 2004, 16(11): 1445-1448 [12] Geng Zhihui, Liu Pukun. Design of a Ka-band second harmonic gyroklystron amplifier by using a self-consistent nonlinear simulation[J]. IEEE Transactions on Plasma Science, 2006, 34(3): 534-540. doi: 10.1109/TPS.2006.875761 [13] Zhou Jun, Liu Dagang, Liao Chen, et al. CHIPIC: an efficient code for electromagnetic PIC modeling and simulation[J]. IEEE Transactions on Plasma Science, 2009, 37(10): 2002-2011. doi: 10.1109/TPS.2009.2026477 [14] 耿志辉. 毫米波回旋速调管放大器的自洽非线性理论与模拟[D]. 北京: 中国科学院研究生院(电子学研究所), 2005Geng Zhihui. Self-consistent nonlinear theory and simulation of millimeter wave gyro-klystron amplifier[D]. Beijing: Institute of Electronic, Chinese Academy of Sciences, 2005 [15] 孙迪敏. W波段三次谐波回旋管理论与实验研究[D]. 北京: 清华大学, 2014Sun Dimin. Theoretical and experimental study of W-band third harmonic gyrotrons[D]. Beijing: Tsinghua University, 2014 -
点击查看大图
图(4) / 表(1)
计量
- 文章访问数: 990
- HTML全文浏览量: 232
- PDF下载量: 38
- 被引次数: 0
