模块化Marx发生器机芯的力学环境适应性分析及优化设计

肖晶; 王海洋; 谢霖燊; 程乐; 孙楚昱; 石凌

doi:10.11884/HPLPB202234.210344

模块化Marx发生器机芯的力学环境适应性分析及优化设计

doi: 10.11884/HPLPB202234.210344

肖晶^{1, 2,},
王海洋^{1, 2},
谢霖燊^{1, 2},
程乐^{1, 2},
孙楚昱^{1, 2},
石凌^{1, 2}

1.
西北核技术研究所，西安 710024
2.
强脉冲辐射环境模拟与效应国家重点实验室，西安 710024

详细信息

作者简介:
肖　晶，xiaojing@nint.ac.cn

中图分类号: TH122；TM832
计量
- 文章访问数: 623
- HTML全文浏览量: 263
- PDF下载量: 49
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-07
- 修回日期: 2022-01-11
- 网络出版日期: 2022-02-12
- 刊出日期: 2022-04-15

Adaptability analysis and optimization design of modular Marx generator in mechanical environment

Xiao Jing^{1, 2
,},
Wang Haiyang^{1, 2},
Xie Linshen^{1, 2},
Cheng Le^{1, 2},
Sun Chuyu^{1, 2},
Shi Ling^{1, 2}

1.
Northwest Institute of Nuclear Technology, Xi’an 710024, China
2.
State Key Laboratory of Intense Pulsed Radiation Simulation and Effect, Xi’an 710024, China

摘要

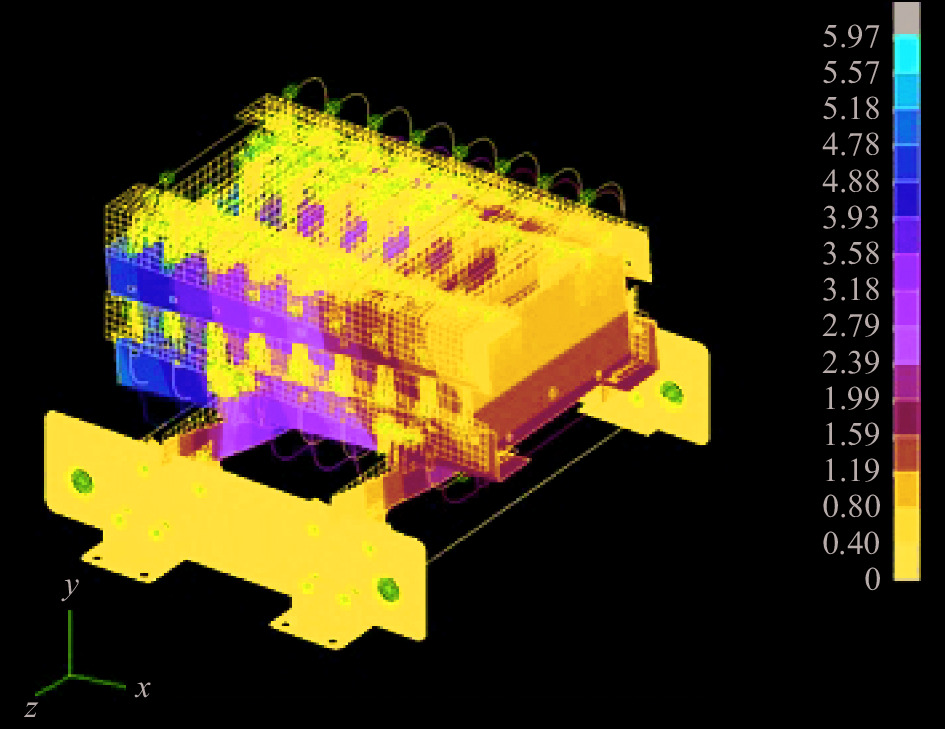
摘要: 为研究Marx发生器机芯在公路运输条件下的力学环境适应性，基于随机振动理论和有限元分析方法对Marx机芯进行了仿真分析和随机振动试验。首先，建立了八级模块化Marx机芯的有限元动力学仿真模型，模拟确定了机芯的应力集中点；然后，通过振动台运输振动摸底试验修正了有限元模型，对机芯结构进行了优化设计，使Marx机芯整体一阶频率由15.4 Hz提高到19.7 Hz，降低了整机垂向的动力学响应，提高了机芯的力学环境适应性。试验结果表明，Marx发生器结构设计需要重点考虑其在垂直方向的可靠性；振动过程中，机芯整体连接稳定，振动应力集中于机芯与U型支撑杆连接处、支撑杆与支撑板连接的角片处，以及开关连接件处，是结构设计的薄弱环节。
- Marx发生器 /
- 随机振动 /
- 有限元分析 /
- 优化设计
Abstract: To study the adaptability of the modularized Marx generator in mechanical environment, simulation and vibration experiment of the generator are conducted based on the random vibration theory and finite element analysis method. Firstly, the finite element simulation model of an 8-stage Marx generator is established, and the stress concentration positions are identified. Secondly, the finite element model is corrected according to the initial results of shaking table test. Then an optimization scheme is proposed to modify the Marx generator. As a result, the first-order frequency of the Marx generator is increased from 15.4 Hz to 19.7 Hz. It is helpful to reduce the dynamic response in vertical direction and enhance the mechanical environment adaptability. Results show that more attention should be paid to the reliability in vertical direction when a Marx generator is being designed. The connection of the generator is stable in the vibration experiment, and the stresses mainly concentrate on the corner pieces between the generator and the U-shape support plates, the connections between U-shape support plates and side support plates, and the switch junctions, which are the weak points in design.
- Marx generator /
- random vibration /
- finite element analysis /
- optimization design

HTML全文

图 1 八级Marx发生器机芯结构图

Figure 1. Structure of the 8-stage Marx generator

下载: 全尺寸图片幻灯片

图 2 单级模块结构示意图

Figure 2. Structure of one stage module

下载: 全尺寸图片幻灯片

图 3 八级Marx发生器机芯一阶模态

Figure 3. First mode of the 8-stage Marx generator

下载: 全尺寸图片幻灯片

图 4 八级Marx发生器机芯二阶模态

Figure 4. Second mode of the 8-stage Marx generator

下载: 全尺寸图片幻灯片

图 5 振动试验系统原理框图

Figure 5. Schematic diagram of the vibration experiment system

下载: 全尺寸图片幻灯片

图 6 x向振动试验前后扫频的加速度曲线

Figure 6. Acceleration curve of frequency sweep before and after the vibration experiment on x axis

下载: 全尺寸图片幻灯片

图 7 振动断裂的角片

Figure 7. Broken angle iron after random vibration experiment

下载: 全尺寸图片幻灯片

图 8 横向M10测点的加速度功率谱密度曲线

Figure 8. Acceleration power spectral density curve at observation point M10 in horizontal direction

下载: 全尺寸图片幻灯片

图 9 Marx发生器机芯结构优化前后比较

Figure 9. Structure of the Marx generator before and after optimization

下载: 全尺寸图片幻灯片

图 10 Marx机芯垂向运输振动监测结果

Figure 10. Monitoring results of the Marx generator in transportation vibration on y axis

下载: 全尺寸图片幻灯片

表 1 材料参数

Table 1. Parameters of the material

material	Young’s modulus/GPa	Poisson ratio	density/(kg·m⁻³)
stainless steel	190.0	0.33	8000
glass fiber reinforced plastics	37.2	0.25	2440
MC nylon	31.9	0.40	1150

下载: 导出CSV

表 2 Marx发生器机芯几个位置的总均方根加速度

Table 2. Acceleration response at several points of the Marx generator

position	total root mean square acceleration/g
position	vertical extraction	lateral extraction	longitudinal extraction
U-shape support pole	2.01	1.55	0.99
support board of glass fiber	2.59	1.29	0.50
switch	1.58	0.89	0.23
random load	1.36	0.58	0.37

下载: 导出CSV

表 3 Marx发生器机芯几个位置的总均方根应力

Table 3. Acceleration response of the Marx generator

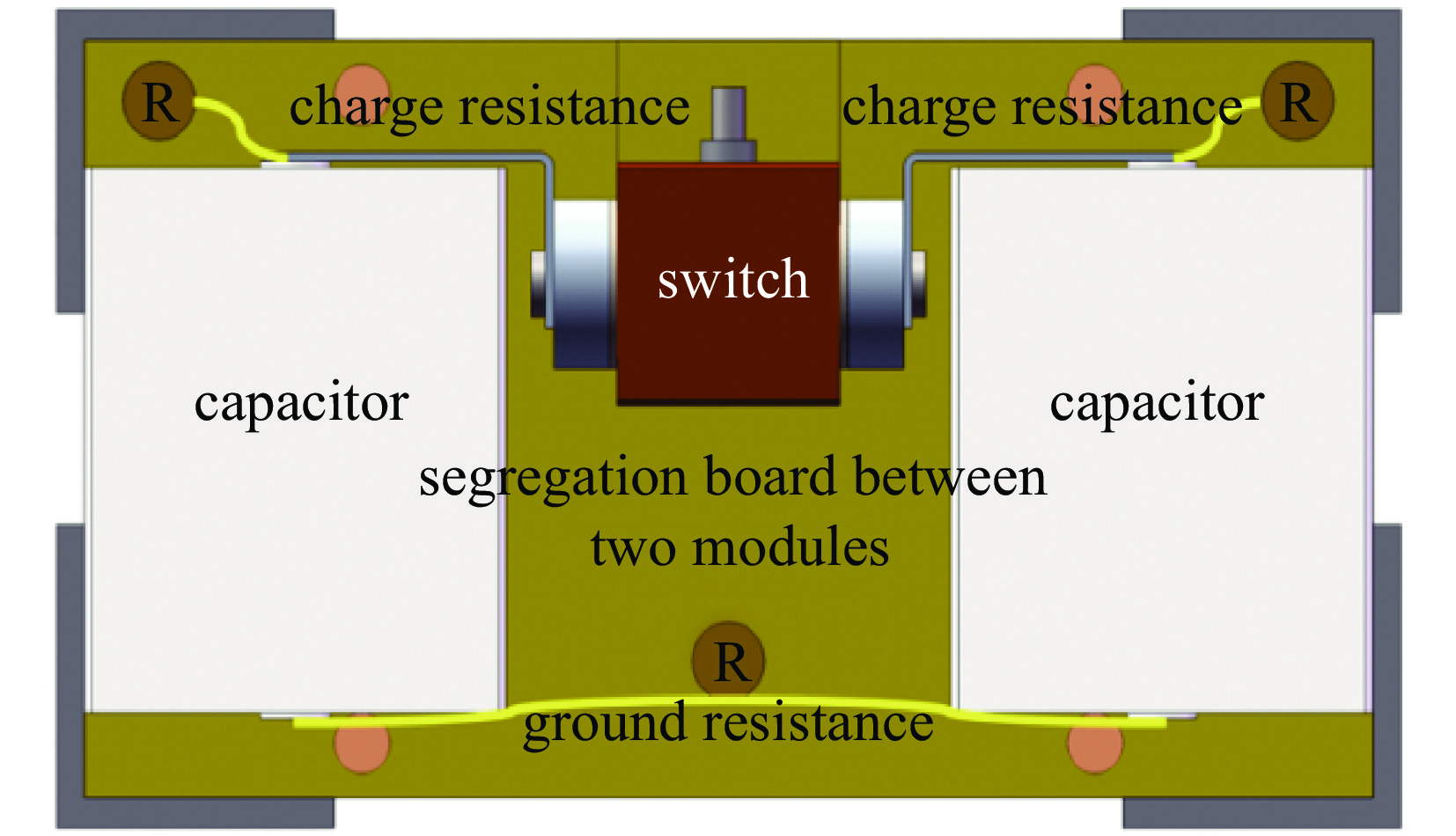
position	total root mean square stress/MPa
position	vertical extraction	lateral extraction	longitudinal extraction
swtich connector	32.2	12.6	7.4
segregation board between two modules	9.8	1.3	6.4
angle plate that connects the angle iron and U-shape support pole	6.8	2.3	1.4
U-shape support pole	0.4	0.1	0.2
angle plate that connects the U-shape support pole and support board of glass fiber	13.3	3.8	4.9

下载: 导出CSV

表 4 改进结构八级Marx机芯垂向随机振动扫频结果

Table 4. Random vibration results of the improved 8-stage Marx pulser in vertical direction

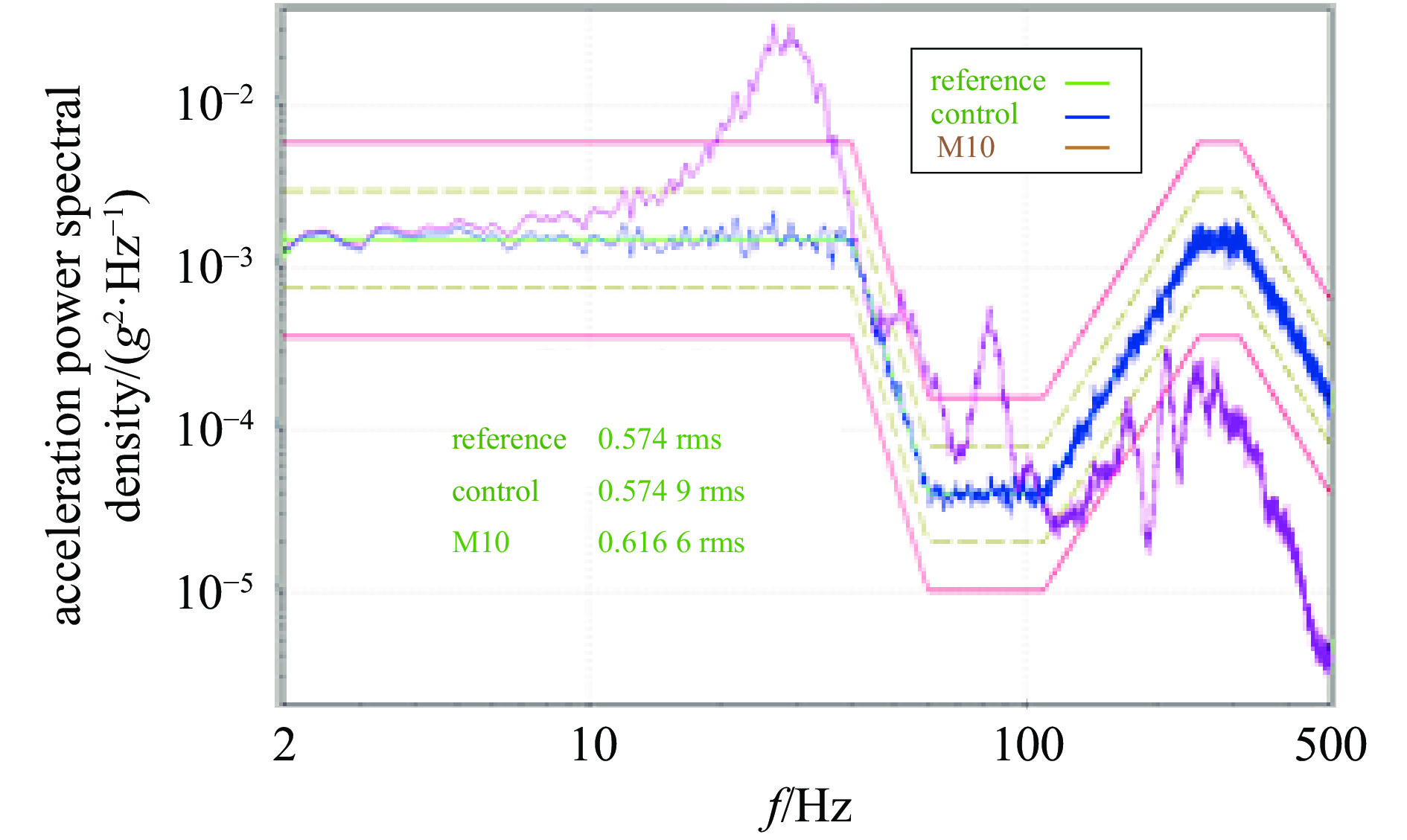
testing positions	root mean square of random vibration/g	magnification factor	1^st sweep frequency/Hz
testing positions	root mean square of random vibration/g	magnification factor	before vibration	after vibration
support board of glass fiber	0.57	2.8	87.8	87.8
angle iron of glass fiber	1.29	6.5	97.9	96.1
U-shape support pole	0.73	3.7	87.8	87.8
switch connector of the 1^st module	2.06	10.3	88.6	87.8
switch and capacitor connectors of the 1^st module	2.00	10.0	88.6	88.6
switch and capacitor connectors of the 4^th module	1.09	5.5	88.6	87.8

下载: 导出CSV

表 5 机芯改进前后整体结构的模态特性

Table 5. Mode characteristic comparison before and after improvement of the Marx generator

modes	frequency/Hz		modal descriptions
modes	before modification	after modification	before modification	after modification
1^st order	15.4	19.7	longitudinal vibration on upper Marx	longitudinal vibration on upper Marx
2^nd order	26.7	30.7	local vibration in switch	local vibration in switch and over all vibration

下载: 导出CSV

参考文献(17)

[1]	Wei Hao, Yin Jiahui, Zhang Pengfei, et al. Development of a 4-MV, 80-kA-induction voltage adder for flash X-ray radiography[J]. IEEE Transactions on Plasma Science, 2019, 47(11): 5030-5036. doi: 10.1109/TPS.2019.2946685
[2]	邓明海, 曹宁翔, 马成刚, 等. 200 kV重复频率Marx发生器研制[J]. 强激光与粒子束, 2019, 31:055003. (Deng Minghai, Cao Ningxiang, Ma Chenggang, et al. Development of 200 kV repetitive Marx generator[J]. High Power Laser and Particle Beams, 2019, 31: 055003 doi: 10.11884/HPLPB201931.190369
[3]	樊旭亮, 孙旭, 潘亚峰, 等. 基于磁开关的固态近方波Marx发生器初步模拟设计[J]. 现代应用物理, 2018, 9:041201. (Fan Xuliang, Sun Xu, Pan Yafeng, et al. Design of a solid state rectangular pulse Marx generator based on magnetic switch[J]. Modern Applied Physics, 2018, 9: 041201
[4]	刘锐, 曾乃工, 王新新. 1.2 MV全封闭Marx发生器的绝缘结构设计[J]. 高电压技术, 2005, 31(4):69-70. (Liu Rui, Zeng Naigong, Wang Xinxin. Insulation design for a 1.2 MV enclosed Marx generator[J]. High Voltage Engineering, 2005, 31(4): 69-70 doi: 10.3969/j.issn.1003-6520.2005.04.026
[5]	Elgenedy M A, Massoud A M, Ahmed S, et al. A modular multilevel voltage-boosting Marx pulse-waveform generator for electroporation applications[J]. IEEE Transactions on Power Electronics, 2019, 34(11): 10575-10589. doi: 10.1109/TPEL.2019.2899974
[6]	宋法伦, 李飞, 龚海涛, 等. 高功率重复频率Marx型脉冲功率源小型化技术研究进展[J]. 强激光与粒子束, 2018, 30:020201. (Song Falun, Li Fei, Gong Haitao, et al. Research progress on miniaturization of high power repetition frequency Marx type pulse power source[J]. High Power Laser and Particle Beams, 2018, 30: 020201 doi: 10.11884/HPLPB201830.170337
[7]	贾伟, 陈志强, 郭帆, 等. 典型布局Marx发生器内部过压形成与分布[J]. 华中科技大学学报(自然科学版), 2018, 46(10):110-115. (Jia Wei, Chen Zhiqiang, Guo Fan, et al. Formation mechanism and distribution of internal overvoltage of Marx generator with typical layouts[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2018, 46(10): 110-115
[8]	Pouncey J C, Lehr J M, Giri D V. Erection of compact Marx generators[J]. IEEE Transactions on Plasma Science, 2019, 47(6): 2902-2909. doi: 10.1109/TPS.2019.2915034
[9]	西北核技术研究所. 一种紧凑型结构的Marx发生器: 103475255A[P]. 2013-12-25 Northwest Inst Nuclear Tech. Marx generator with compact structure: 103475255A[P]. 2013-12-25
[10]	Sharma J K. Theoretical and experimental modal analysis of beam[M]//Ray K, Sharan S, Rawat S, et al. Engineering Vibration, Communication and Information Processing. Singapore: Springer, 2019: 177-186.
[11]	瞿金秀, 石长全, 王磊超, 等. 不同老化状态黏弹夹层结构的模态分析[J]. 振动与冲击, 2020, 39(11):69-75. (Qu Jinxiu, Shi Changquan, Wang Leichao, et al. Modal analysis of viscoelastic sandwich structure with different aging states[J]. Journal of Vibration and Shock, 2020, 39(11): 69-75
[12]	韩帅, 曹亚文, 邓长华, 等. 液体火箭发动机三轴向虚拟振动试验技术研究[J]. 火箭推进, 2018, 44(6):68-74. (Han Shuai, Cao Yawen, Deng Changhua, et al. Research on test technology for three-axial virtual vibration of liquid rocket engine[J]. Journal of Rocket Propulsion, 2018, 44(6): 68-74 doi: 10.3969/j.issn.1672-9374.2018.06.011
[13]	顾乾磊, 张万福, 张尧, 等. 基于微元轨迹的密封动力特性系数理论识别方法[J]. 振动与冲击, 2019, 38(16):22-28. (Gu Qianlei, Zhang Wanfu, Zhang Yao, et al. A theoretical identification method for dynamic coefficients of seals based on infinitesimal trajectory of rotors[J]. Journal of Vibration and Shock, 2019, 38(16): 22-28
[14]	李勤建, 高翠琢, 边国辉. 组件的模态分析和随机振动分析[J]. 半导体技术, 2012, 37(10):810-814. (Li Qinjian, Gao Cuizhuo, Bian Guohui. Modal analysis and random vibration analysis on a module[J]. Semiconductor Technology, 2012, 37(10): 810-814 doi: 10.3969/j.issn.1003-353x.2012.10.015
[15]	张建斌. 带橡胶减振器的箭载电子设备动力学响应分析研究[D]. 哈尔滨: 哈尔滨工业大学, 2019 Zhang Jianbin. Research on dynamic response of the electronic equipment with Bubber shock absorber on the rockets[D]. Harbin: Harbin Institute of Technology, 2019
[16]	Randall R B, Antoni J, Smith W A. A survey of the application of the cepstrum to structural modal analysis[J]. Mechanical Systems and Signal Processing, 2019, 118: 716-741. doi: 10.1016/j.ymssp.2018.08.059
[17]	李星占, 董兴建, 岳晓斌, 等. 振动响应传递率的动力学特性研究及其在工作模态分析中的应用[J]. 振动与冲击, 2019, 38(9):62-70. (Li Xingzhan, Dong Xingjian, Yue Xiaobin, et al. Dynamic characteristics of vibration response transmissibility and its application in operational modal analysis[J]. Journal of Vibration and Shock, 2019, 38(9): 62-70