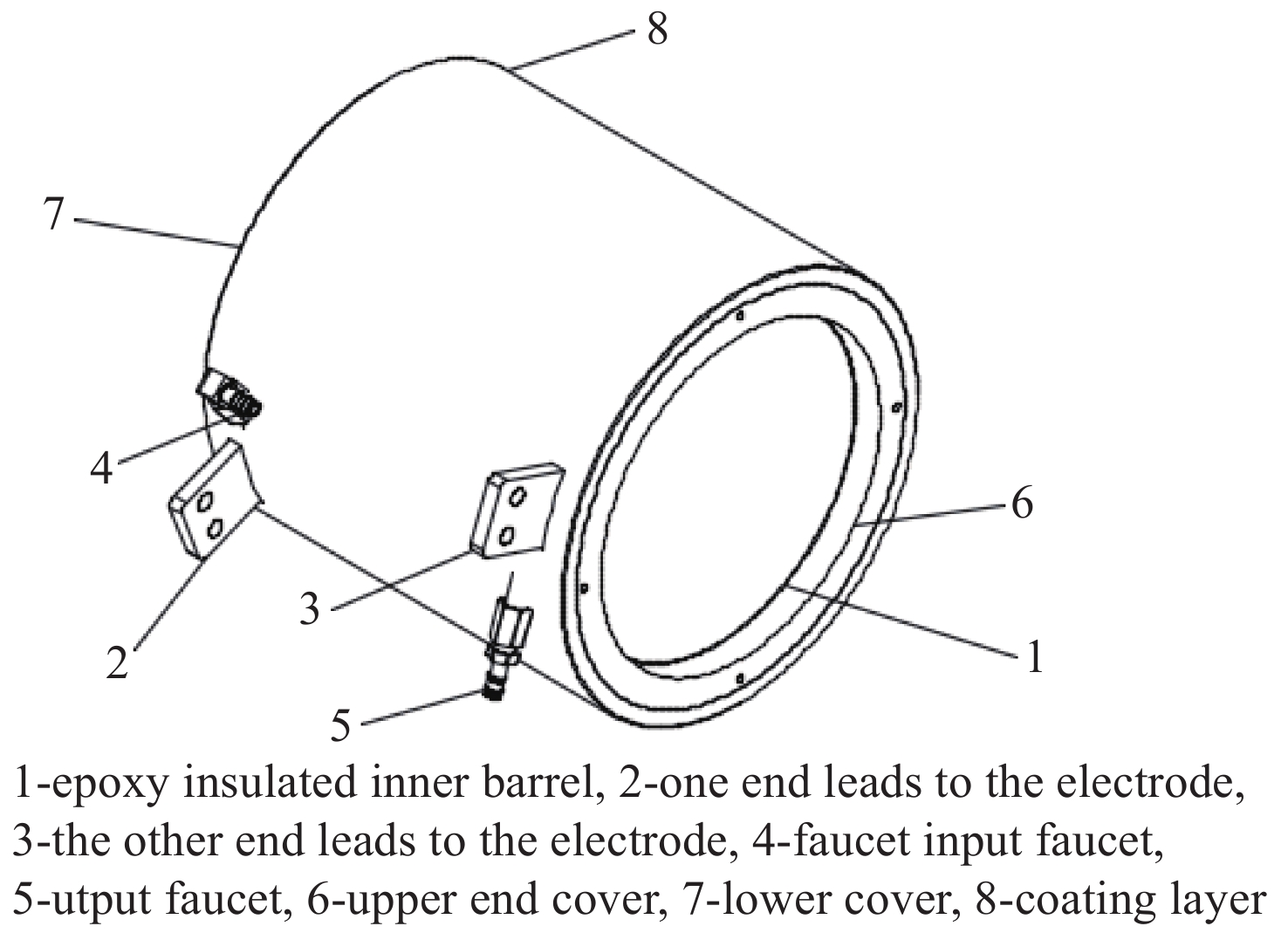
Design and analysis of repetitive frequency inductor in high power and high energy storage pulse power supply
-
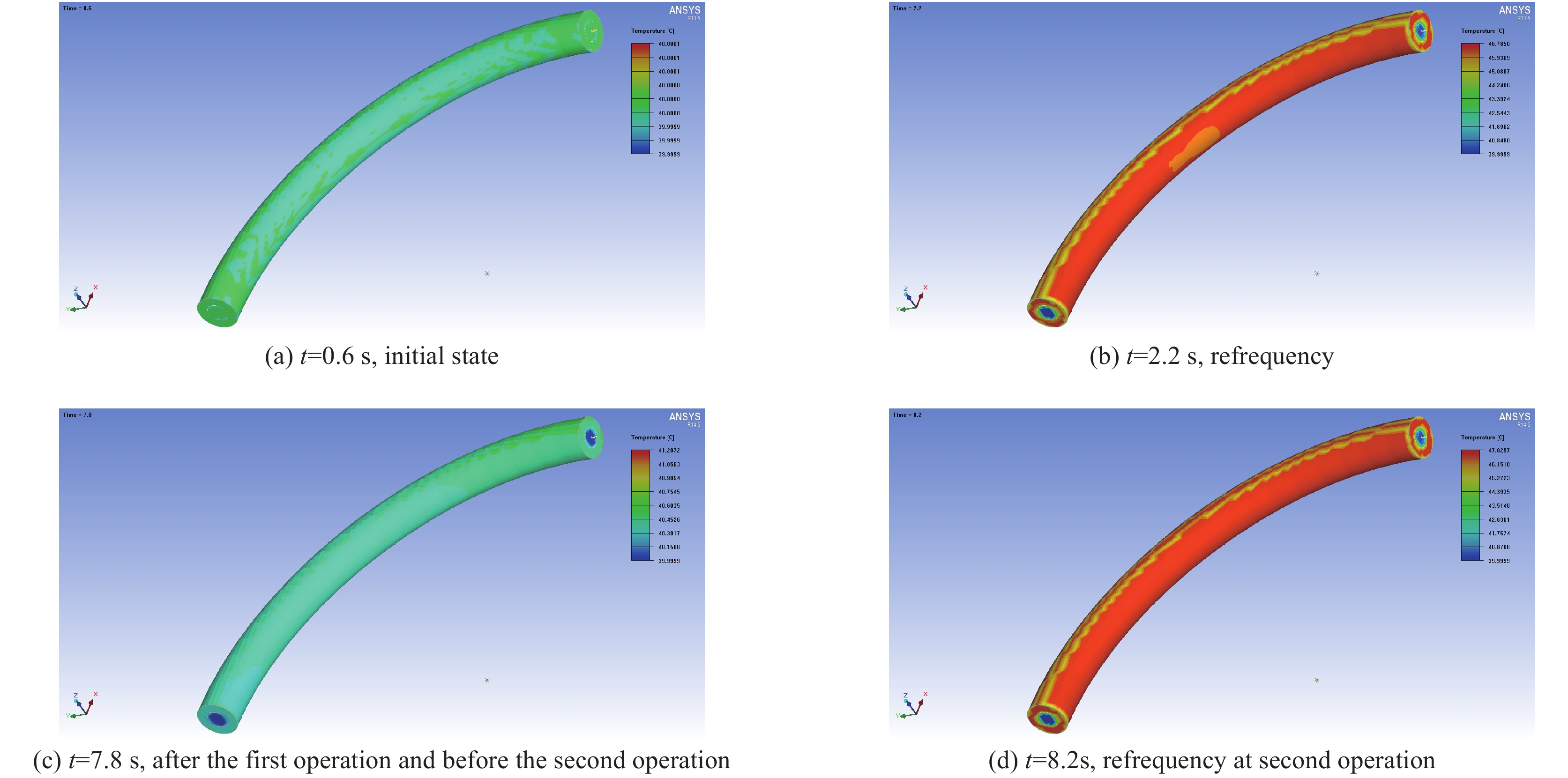
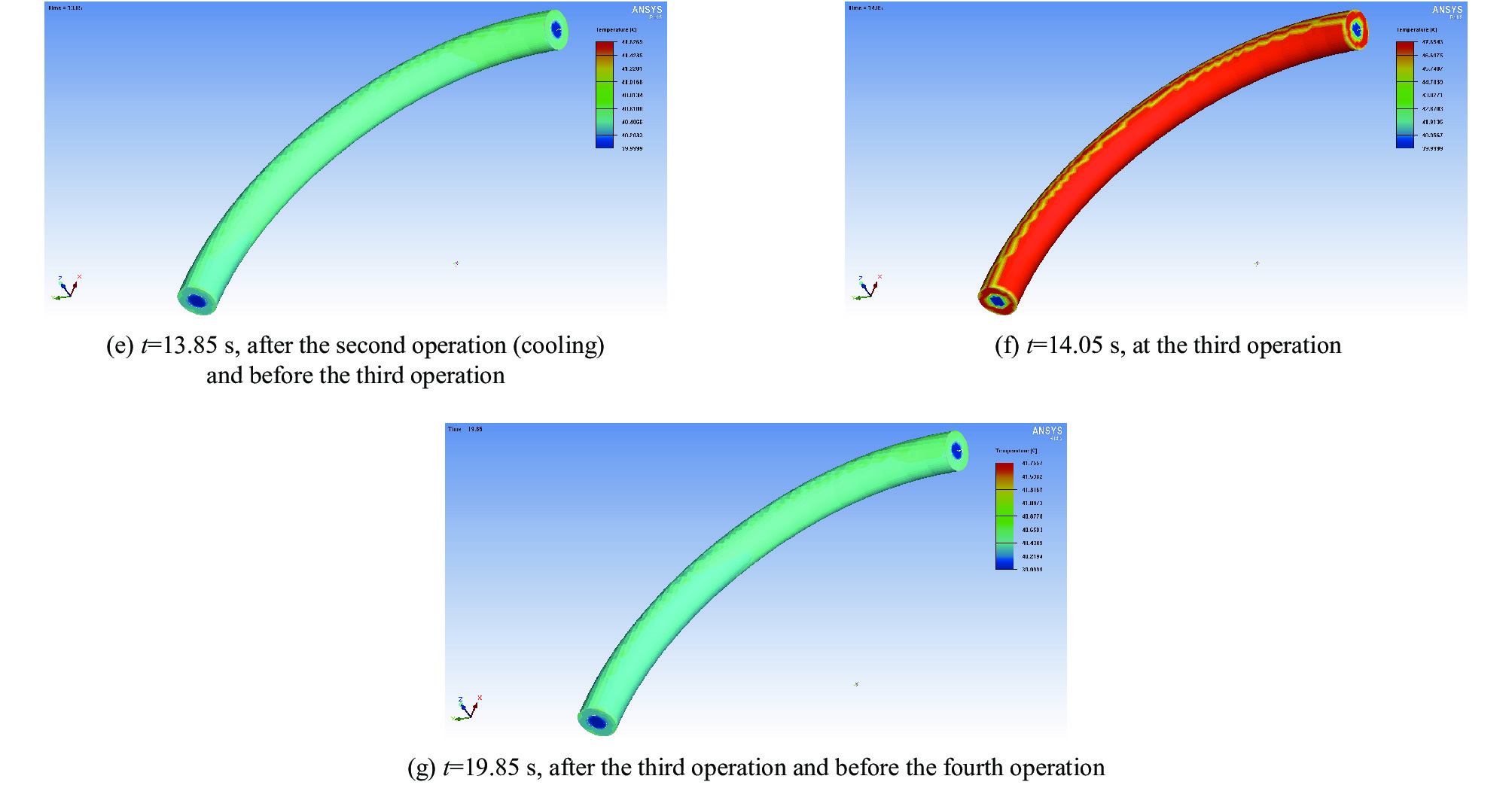
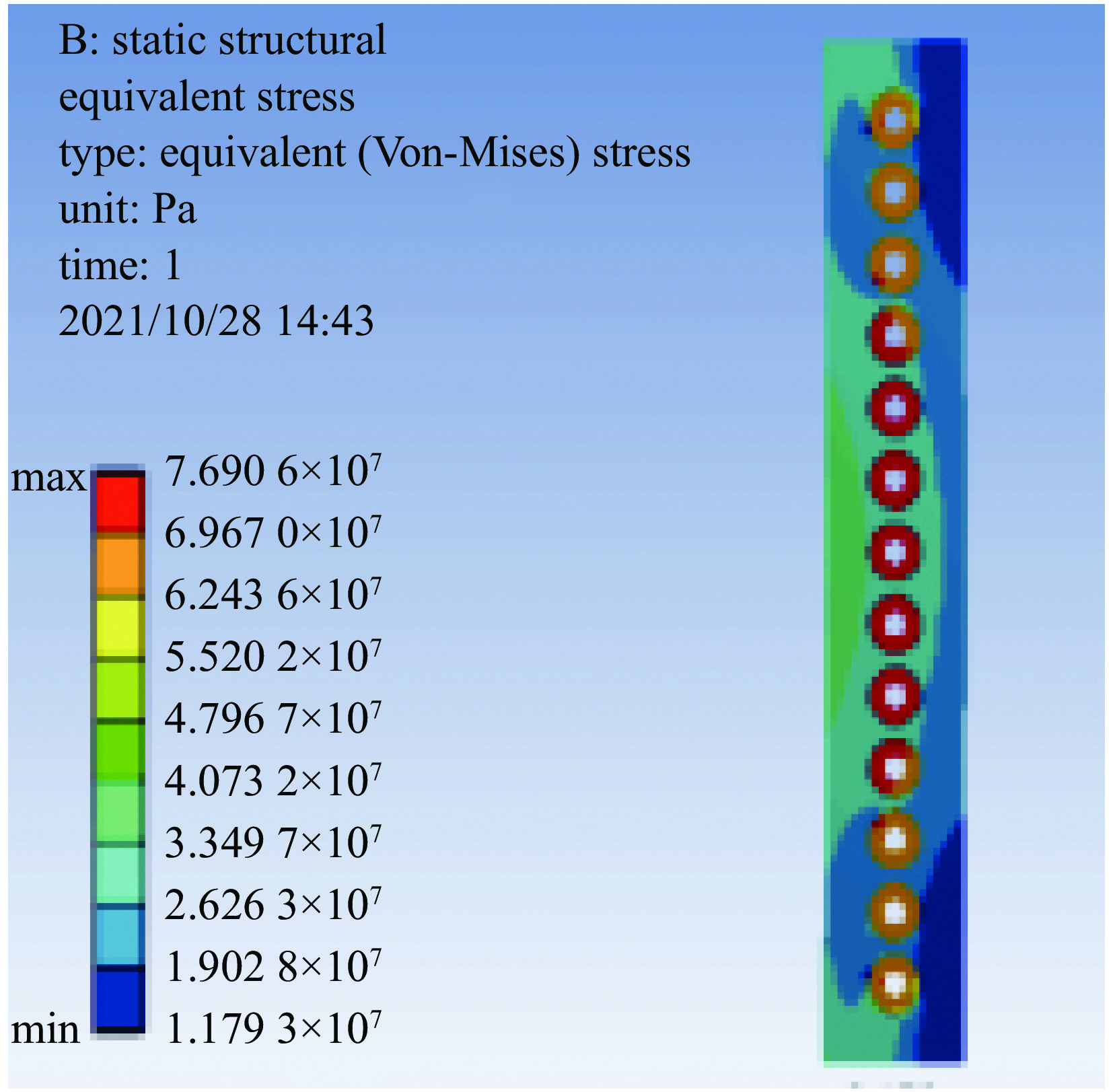
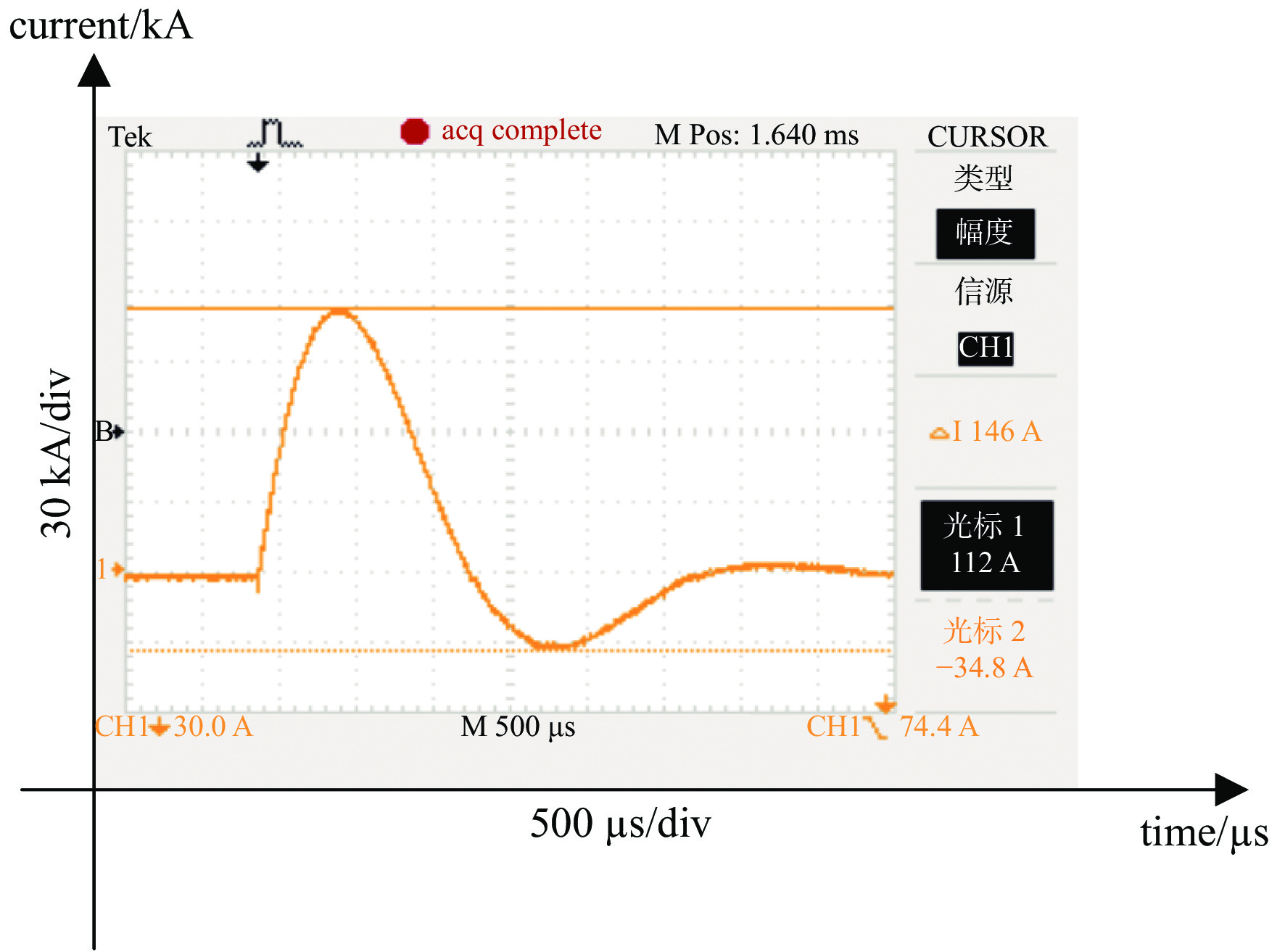
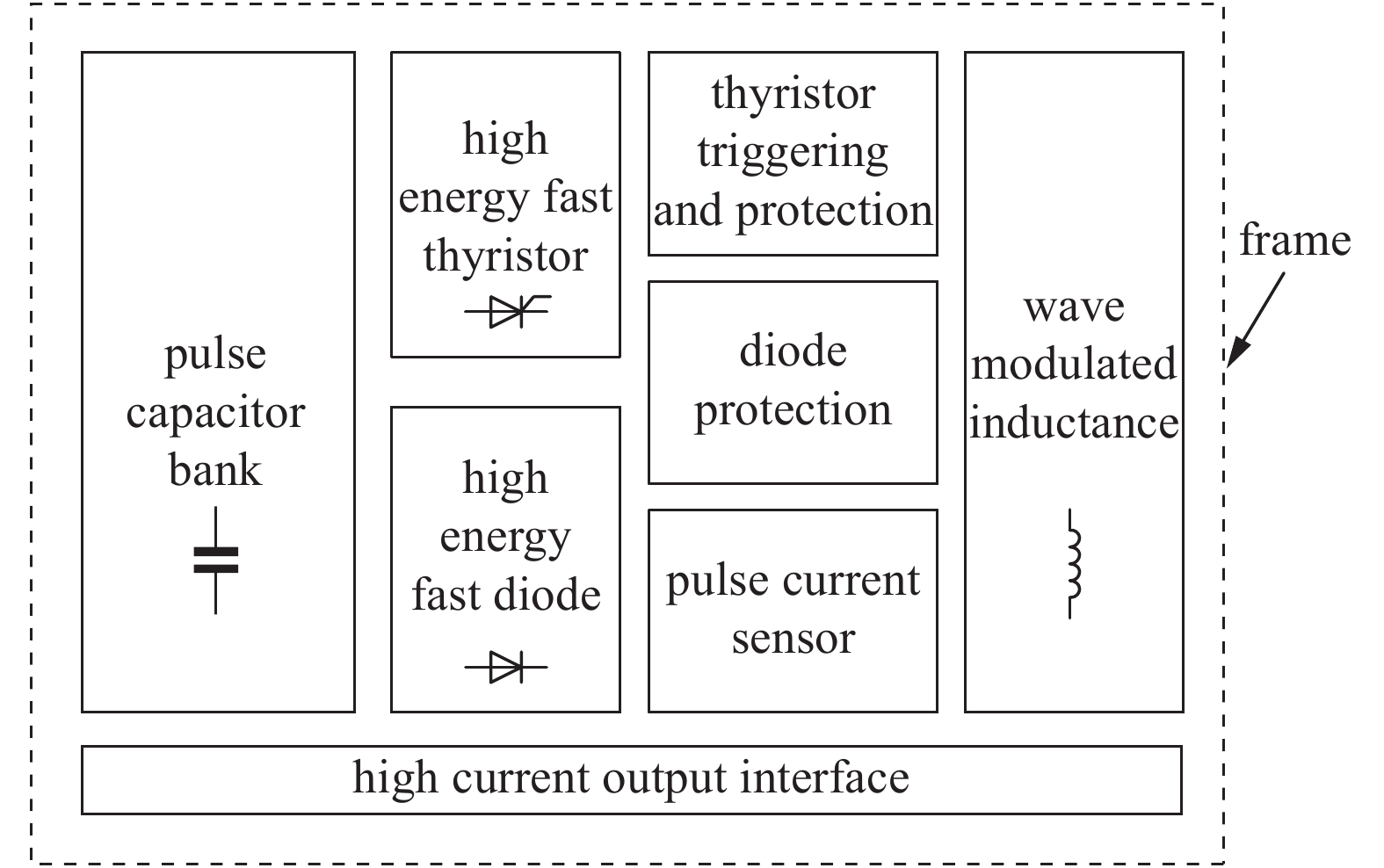
摘要: 针对高功率脉冲电源集成系统连续放电的需求，研制了一种用于该系统的重频水冷电感。水冷电感在系统中既调节电源的电流波形，又能起到隔离作用。该重频水冷电感耐压高、通流大、充电间隔周期6 s，可连续工作10 次放电。针对连续放电的需求，通过去离子循环水对重频电感进行降温。现以单模块能量334 kJ、电感量30 µH、通流 100 kA为例进行设计分析，建立重频水冷电感温度场仿真模型，通过ANSYS仿真软件对该电感内部温度瞬态特性进行分析。结果表明：水冷电感通过去离子水冷却效果好，电感每次工作后温度最高达到47 ℃，在下一个工作点到来之前电感温度又恢复到41 ℃；同时该电感在没有加循环水的情况下通过了112 kA的电动力考核。试验结果与理论分析吻合较好，重频水冷电感运行稳定，从而验证了理论分析和设计的正确性。Abstract: To meet the requirement of continuous discharge in the integrated system of high power pulse power supply a repeatitive frequency water-cooled inductor for the system was developed. In the system, the water-cooled inductor can not only adjust the current waveform of the power supply, but also play an isolation role. The repeatitive frequency water-cooled inductor can withstand high voltage, large current, charge interval period of 6 seconds, and can work continuously for 10 times of discharge capacity. To meet the requirement of continuous discharge, deionized circulating water is used to cool the inductor. Taking the single module energy of 334 kJ, inductance of 30 μH, and current of 100 kA as an example, the design and analysis are carried out to establish the temperature field simulation model of the inductor, and analysis is made on the transient characteristics of the internal temperature of the inductor through ANSYS simulation software. The results show that the inductor is well cooled by deionized water, and the maximum temperature of the inductor reaches 47 ℃ after each operation, and the temperature of the inductor recovers to 41 ℃ before the next operation point. At the same time, the inductor passes the 112 kA electrodynamic test without circulating water. The experimental results agree well with the theoretical analysis, and the inductor runs stably, which verifies the correctness of theoretical analysis and design.
-
图 2 重频水冷电感外形图
Figure 2. Contour diagram of the repeatitive frequency water-cooled inductor
图 3 重频水冷电感三维图
Figure 3. 3D diagram of the repeatitive frequency water- cooled inductor
图 6 重频水冷电感温度分布云图
Figure 6. Cloud map of temperature distribution of the repeatitive frequency water-cooled inductor
图 9 重频水冷电感通流试验原理图
Figure 9. Schematic diagram of repeatitive frequency water-cooled inductor test circuit
图 10 重频水冷电感通流试验接线图
Figure 10. Wiring diagram of repeatitive frequency water cooled inductor flow test
图 11 重频水冷电感通过了112 kA电流峰值的波形图
Figure 11. Waveform of repeatitive frequency water-cooled inductor passing a peak current of 112 kA
表 1 导线线径与温升的关系
Table 1. Relationship between wire diameter and temperature rise
number Фo/mm Фi/mm energy/kJ temperature/℃ 1 14 6 267 52.96 
下载: 导出CSV
表 2 趋肤深度与铜管水温、频率的关系
Table 2. Relationship between skin depth and temperature and frequency
number frequency/Hz temperature/℃ temperature of coefficient/K skin depth/mm 1 200 47/40
47/401.1154/1.0853
1.1154/1.08533.707 2 166.7 4.117
下载: 导出CSV
表 3 电感流量特性实验数据表
Table 3. Experimental data of inductance flow characteristics
flow rate/(L/min) pressure loss/MPa 5 0.257 5.5 0.309 6 0.364 6.5 0.413 7 0.512
下载: 导出CSV
-
[1] Akiyama H, Sakugawa T, Namihira T, et al. Industrial applications of pulsed power technology[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(5): 1051-1064. doi: 10.1109/TDEI.2007.4339465 [2] 戴宇峰, 鲁军勇, 张晓, 等. 脉冲功率电源连续发射水冷模拟负载[J]. 国防科技大学学报, 2016, 38(6):6-11. (Dai Yufeng, Lu Junyong, Zhang Xiao, et al. Water-cooling simulated resistance for continuously launching pulsed power supply[J]. Journal of National University of Defense Technology, 2016, 38(6): 6-11 doi: 10.11887/j.cn.201606002 [3] Hundertmark S, Liebfried O. Options for an electric launcher system[J]. IEEE Transactions on Plasma Science, 2019, 47(10): 4433-4438. doi: 10.1109/TPS.2018.2888899 [4] Li Zhenxiao, Zhang Yazhou, Wu Jinguo, et al. Design of a 30MJ capacitor-based pulsed power supply for EML[C]//Proceedings of the 21st International Conference on Pulsed Power. Brighton, UK: IEEE, 2017: 1-5. [5] Lehmann P, Peter H, Wey J. First experimental results with the ISL 10 MJ DES railgun PEGASUS[J]. IEEE Transactions on Magnetics, 2001, 37(1): 435-439. doi: 10.1109/20.911871 [6] Hundertmark S, Schneider M, Simicic D, et al. Experiments to increase the used energy with the PEGASUS railgun[J]. IEEE Transactions on Plasma Science, 2014, 42(10): 3180-3185. doi: 10.1109/TPS.2014.2314131 [7] 张龙霞, 李碧清, 霍敏. 国外电磁炮发展概述[J]. 飞航导弹, 2011, 40(10):23-27. (Zhang Longxia, Li Biqing, Huo Min. Overview of foreign electromagnetic gun development[J]. Maneuverable Missile, 2011, 40(10): 23-27 [8] 范晶, 宋朝文. 舰载电磁轨道炮用高功率脉冲电源研究进展[J]. 电气技术, 2010(s1):70-72. (Fan Jing, Song Chaowen. Research progress of the high-powered pulsed power supply of naval electromagnetic rail gun[J]. Electrical Engineering, 2010(s1): 70-72 [9] 何巧, 马游春, 马子光, 等. 高功率脉冲电源电压测试系统设计[J]. 仪表技术与传感器, 2020(2):46-49,113. (He Qiao, Ma Youchun, Ma Ziguang, et al. Design of high power pulse power supply voltage test system[J]. Instrument Technique and Sensor, 2020(2): 46-49,113 doi: 10.3969/j.issn.1002-1841.2020.02.011 [10] Conway J T. Inductance calculations for circular coils of rectangular cross section and parallel axes using Bessel and Struve functions[J]. IEEE Transactions on Magnetics, 2010, 46(1): 75-81. doi: 10.1109/TMAG.2009.2026574 [11] Conway J T. Inductance calculations for noncoaxial coils using Bessel functions[J]. IEEE Transactions on Magnetics, 2007, 43(3): 1023-1034. doi: 10.1109/TMAG.2006.888565 [12] Conway J T. Analytical solutions for the self- and mutual inductances of concentric coplanar disk coils[J]. IEEE Transactions on Magnetics, 2013, 49(3): 1135-1142. doi: 10.1109/TMAG.2012.2229287 [13] Luo Yao, Chen Baichao. Improvement of self-inductance calculations for circular coils of rectangular cross section[J]. IEEE Transactions on Magnetics, 2013, 49(3): 1249-1255. doi: 10.1109/TMAG.2012.2228499 [14] Babic S, Salon S, Akyel C. The mutual inductance of two thin coaxial disk coils in air[J]. IEEE Transactions on Magnetics, 2004, 40(2): 822-825. doi: 10.1109/TMAG.2004.824810 [15] 卡兰塔罗夫, 采依特林. 电感计算手册[M]. 陈汤铭, 刘保安, 罗应立, 等译. 北京: 机械工业出版社, 1992КалантаровП. Л. , ЦейтлинЛ. А. Расчет индуктивностей справочаи книга[M]. Chen Tangming, Liu Baoan, Luo Yingli, et al, trans. Beijing: China Machine Press, 1992 [16] 罗垚, 陈柏超, 袁佳歆, 等. 倾斜轴空心矩形截面圆柱线圈互感计算[J]. 电工技术学报, 2012, 27(5):132-136. (Luo Yao, Chen Baichao, Yuan Jiaxin, et al. Mutual inductance calculations of inclined axial air-core circular coils with rectangular cross-sections[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 132-136 [17] 罗垚, 陈柏超. 空心矩形截面圆柱线圈自感计算的新方法[J]. 电工技术学报, 2012, 27(6):1-5. (Luo Yao, Chen Baichao. New method for self-inductance calculations of air-core circular coils with rectangular cross-sections[J]. Transactions of China Electrotechnical Society, 2012, 27(6): 1-5 [18] 罗垚, 陈柏超, 周洪. 有限长圆柱磁屏同轴线圈电感计算方法[J]. 电工技术学报, 2016, 31(14):122-129. (Luo Yao, Chen Baichao, Zhou Hong. Approach for inductance calculations of coaxial circular coils shielded by cylindrical magnetic screen of finite length[J]. Transactions of China Electrotechnical Society, 2016, 31(14): 122-129 doi: 10.3969/j.issn.1000-6753.2016.14.014 -
点击查看大图
计量
- 文章访问数: 869
- HTML全文浏览量: 352
- PDF下载量: 111
- 被引次数: 0
