双束等离子体尾波加速中的束流相对能散预测

王晓宁; 高杰; 安维明; 王佳; 李大章; 曾明; 鲁巍

doi:10.11884/HPLPB202234.210425

双束等离子体尾波加速中的束流相对能散预测

doi: 10.11884/HPLPB202234.210425

王晓宁^{1, 2,},
高杰^{1, 2},
安维明^3, ,,
王佳^{1, 2},
李大章^{1, 2, ,},
曾明^{1, 2},
鲁巍⁴

1.
中国科学院高能物理研究所, 北京 100049
2.
中国科学院大学, 北京 100049
3.
北京师范大学天文系, 北京 100875
4.
清华大学工程物理系, 北京100084

基金项目: 国家自然科学基金项目(12075030, 11975252); 中国科学院前沿科学重点研究计划项目(QYZDJ-SSW-SLH004)；中国科学院人才引进计划(E05153U1); 中国科学院高能物理研究所创新基金项目(Y954516)

详细信息

作者简介:
王晓宁，wangxiaoning@ihep.ac.cn

通讯作者:
安维明，anweiming@bnu.edu.cn

李大章，lidz@ihep.ac.cn

中图分类号: TF806
计量
- 文章访问数: 864
- HTML全文浏览量: 257
- PDF下载量: 67
- 被引次数: 0
出版历程
- 收稿日期: 2021-10-10
- 修回日期: 2021-12-23
- 录用日期: 2022-01-06
- 网络出版日期: 2022-01-27
- 刊出日期: 2022-03-19

Predicting relative energy spread in two-bunch plasma wakefield acceleration

Wang Xiaoning^{1, 2
,},
Gao Jie^{1, 2},
An Weiming^{3
, ,},
Wang Jia^{1, 2},
Li Dazhang^{1, 2
, ,},
Zeng Ming^{1, 2},
Lu Wei⁴

1.
Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
2.
University of Chinese Academy of Sciences, Beijing 100049, China
3.
Department of Astronomy, Beijing Normal University, Beijing 100875, China
4.
Department of Engineering Physics, Tsinghua University, Beijing 100084, China

摘要

摘要: 针对空泡机制中的双束等离子体尾波电子加速设计，给出了能够快速得到被加速束流在最大加速距离下的相对能散的预测公式。通过加速初始时刻束流纵向分布以及束流所处位置的纵向尾波场可得到束流最终相对能散。该预测公式不仅可应用于驱动束流与被加速束流初始能量相同的情况，还可应用于两个束流初始能量不相同的情况。由该预测公式得到的束流相对能散与被加速束流和驱动束流的初始能量的比值有关，而与两个束流初始能量的数值无关。利用准静态近似的粒子网格模拟程序QuickPIC对理论进行了模拟验证，模拟结果与理论预期结果一致。
- 等离子体尾波加速 /
- 电子加速 /
- 双束团 /
- 相对能散 /
- 粒子网格模拟
Abstract: We present a formula to directly obtain the final relative energy spread of a trailing beam at the maximal acceleration distance. The formula works for electron beams in a two-bunch plasma wakefield acceleration stage in the so-called nonlinear bubble regime. It only requires the longitudinal profile of the trailing beam and the longitudinal wakefield within the trailing beam at the beginning of an acceleration. This formula not only works well for drive beams and trailing beams with the same initial energies, but is also available for those beams with different initial energies. We find that the relative energy spread of the trailing beam obtained from the formula is determined by the ratio of the trailing beam’s initial energy to the drive beam’s initial energy rather than the specific value of their initial energies. We perform several computational simulations using the quasi-static particle-in-cell code QuickPIC, and the results agree well with that calculated from the formula.
- plasma wakefield acceleration /
- electron acceleration /
- two-bunch /
- relative energy spread /
- particle-in-cell simulation

HTML全文

图 1 D = 1时加速开始时刻以及达到最大加速距离时刻等离子体中的尾波结构

Figure 1. Wake structure in the plasma at the beginning and at the maximal acceleration distance of an acceleration at D = 1

下载: 全尺寸图片幻灯片

图 2 D = 2时在最大加速距离时刻 (a) 驱动束流初始能量为10 GeV和 (b) 驱动束流初始能量为5 GeV的等离子体中的尾波结构

Figure 2. Wake structure in the plasma for (a) drive beam’s initial energy is 10 GeV and (b) drive beam’s initial energy is 5 GeV at the maximal acceleration distance of an acceleration at D = 2

下载: 全尺寸图片幻灯片

表 1 PIC模拟和式（3）得到的相对能散

Table 1. Relative energy spread from PIC simulations and equation (3)

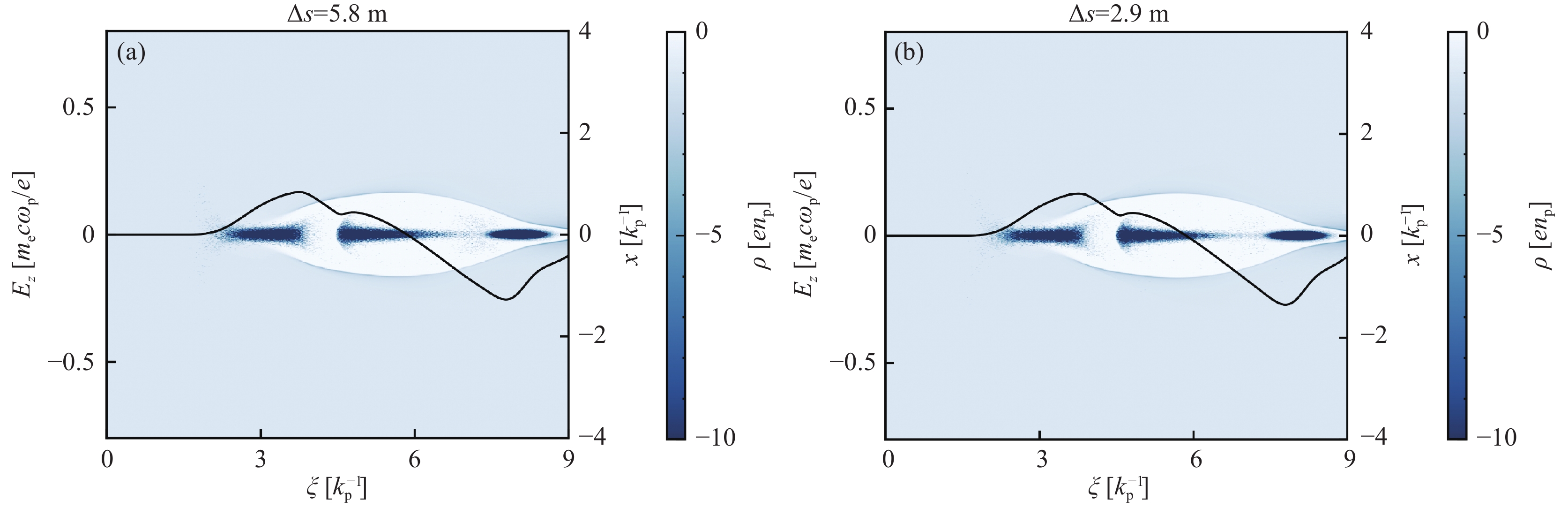
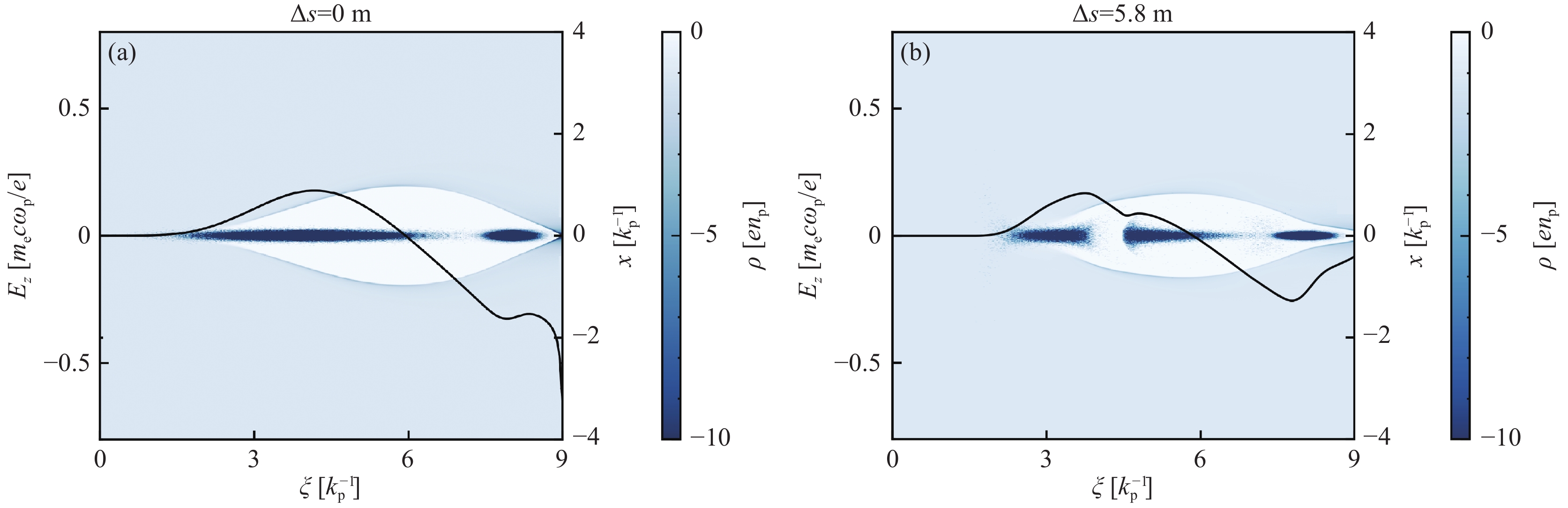
$ D $	drive beam					$ d/{\text{k}}_{\text{p}}^{-1} $	trailing beam					$ \vartriangle s/{\text{m}} $	$ {\delta _{Er}}/{\text{{\text{%}} }} $	$ {\delta _{Ep}}/{\text{{\text{%}} }} $
$ D $	$ {W_{ds}}/{\text{GeV}} $	$ {\sigma _{ {\textit{z}} d}}/{\text{k}}_{\text{p}}^{-1} $	$ {n_{bd}}/{{\text{n}}_{\text{p}}} $	$ {\varepsilon _{Nd}}/{\text{k}}_{\text{p}}^{-1} $	$ {\sigma _{r{\text{d}}}}/{\text{k}}_{\text{p}}^{-1} $	$ d/{\text{k}}_{\text{p}}^{-1} $	$ {W_{ts}}/{\text{GeV}} $	$ {\sigma _{ {\textit{z}} t}}/{\text{k}}_{\text{p}}^{-1} $	$ {n_{bt}}/{{\text{n}}_{\text{p}}} $	$ {\varepsilon _{Nt}}/{\text{k}}_{\text{p}}^{-1} $	$ {\sigma _{rt}}/{\text{k}}_{\text{p}}^{-1} $	$ \vartriangle s/{\text{m}} $	$ {\delta _{Er}}/{\text{{\text{%}} }} $	$ {\delta _{Ep}}/{\text{{\text{%}} }} $
1	10	1	80	0.25	0.05	4	10	0.25	76.36	0.25	0.05	5.8	2.33	2.36
2	10	1	80	0.25	0.05	4	20	0.25	76.36	0.35	0.05	5.8	1.72	1.74
2	5	1	80	0.17	0.05	4	10	0.25	76.36	0.25	0.05	2.9	1.72	1.74

下载: 导出CSV

参考文献(20)

[1]	Tajima T, Dawson J M. Laser electron accelerator[J]. Physical Review Letters, 1979, 43(4): 267-270. doi: 10.1103/PhysRevLett.43.267
[2]	Chen P, Dawson J M, Huff R W, et al. Acceleration of electrons by the interaction of a bunched electron beam with a plasma[J]. Physical Review Letters, 1985, 54(7): 693-696. doi: 10.1103/PhysRevLett.54.693
[3]	Rosenzweig J B, Breizman B, Katsouleas T, et al. Acceleration and focusing of electrons in two-dimensional nonlinear plasma wake fields[J]. Physical Review A, 1991, 44(10): R6189-R6192. doi: 10.1103/PhysRevA.44.R6189
[4]	Lu Wei, Huang Chengkun, Zhou Miaomiao, et al. Nonlinear theory for relativistic plasma wakefields in the blowout regime[J]. Physical Review Letters, 2006, 96: 165002. doi: 10.1103/PhysRevLett.96.165002
[5]	Lu Wei, Huang Chengkun, Zhou Miaomiao, et al. A nonlinear theory for multidimensional relativistic plasma wave wakefields[J]. Physics of Plasmas, 2006, 13: 056709. doi: 10.1063/1.2203364
[6]	Hogan M J, Assmann R, Decker F J, et al. E-157: a 1.4-m-long plasma wake field acceleration experiment using a 30 GeV electron beam from the Stanford Linear Accelerator Center Linac[J]. Physics of Plasmas, 2000, 7(5): 2241-2248. doi: 10.1063/1.874059
[7]	Muggli P, Lee S, Katsouleas T, et al. Collective refraction of a beam of electrons at a plasma-gas interface[J]. Physical Review Special Topics-Accelerators and Beams, 2001, 4: 091301. doi: 10.1103/PhysRevSTAB.4.091301
[8]	Clayton C E, Blue B E, Dodd E S, et al. Transverse envelope dynamics of a 28.5-GeV electron beam in a long plasma[J]. Physical Review Letters, 2002, 88: 154801. doi: 10.1103/PhysRevLett.88.154801
[9]	Hogan M J, Clayton C E, Huang Chengkun, et al. Ultrarelativistic-positron-beam transport through meter-scale plasmas[J]. Physical Review Letters, 2003, 90: 205002. doi: 10.1103/PhysRevLett.90.205002
[10]	Blue B E, Clayton C E, O'Connell C L, et al. Plasma-wakefield acceleration of an intense positron beam[J]. Physical Review Letters, 2003, 90: 214801. doi: 10.1103/PhysRevLett.90.214801
[11]	Muggli P, Blue B E, Clayton C E, et al. Meter-scale plasma-wakefield accelerator driven by a matched electron beam[J]. Physical Review Letters, 2004, 93: 014802. doi: 10.1103/PhysRevLett.93.014802
[12]	Litos M, Adli E, An Weiming, et al. High-efficiency acceleration of an electron beam in a plasma wakefield accelerator[J]. Nature, 2014, 515(7525): 92-95. doi: 10.1038/nature13882
[13]	Corde S, Adli E, Allen J M, et al. Multi-gigaelectronvolt acceleration of positrons in a self-loaded plasma wakefield[J]. Nature, 2015, 524(7566): 442-445. doi: 10.1038/nature14890
[14]	Seryi A, Hogan M, Pei Shilun, et al. A concept of plasma wake field acceleration linear collider (PWFA-LC)[R]. SLAC-PUB-13766, 2009.
[15]	Fonseca R A, Silva L O, Tsung F S, et al. OSIRIS: a three-dimensional, fully relativistic particle in cell code for modeling plasma based accelerators[C]//Proceedings of International Conference on Computational Science. Amsterdam: Springer, 2002: 342-351.
[16]	Huang Chengkun, Decyk V K, Ren C, et al. QUICKPIC: a highly efficient particle-in-cell code for modeling wakefield acceleration in plasmas[J]. Journal of Computational Physics, 2006, 217(2): 658-679. doi: 10.1016/j.jcp.2006.01.039
[17]	An Weiming, Decyk V K, Mori W B, et al. An improved iteration loop for the three dimensional quasi-static particle-in-cell algorithm: QuickPIC[J]. Journal of Computational Physics, 2013, 250: 165-177. doi: 10.1016/j.jcp.2013.05.020
[18]	https://gitee.com/bnu-plasma-astrophysics-sg/quick-pic-open-source.git.
[19]	Joshi C, Blue B, Clayton C E, et al. High energy density plasma science with an ultrarelativistic electron beam[J]. Physics of Plasmas, 2002, 9(5): 1845-1855. doi: 10.1063/1.1455003
[20]	Bane K L F, Chen P, Wilson P B. On collinear wake field acceleration[J]. IEEE Transactions on Nuclear Science, 1985, 32(5): 3524-3526. doi: 10.1109/TNS.1985.4334416