Influence of energy spread on the transverse profile of the focused electron beam
-
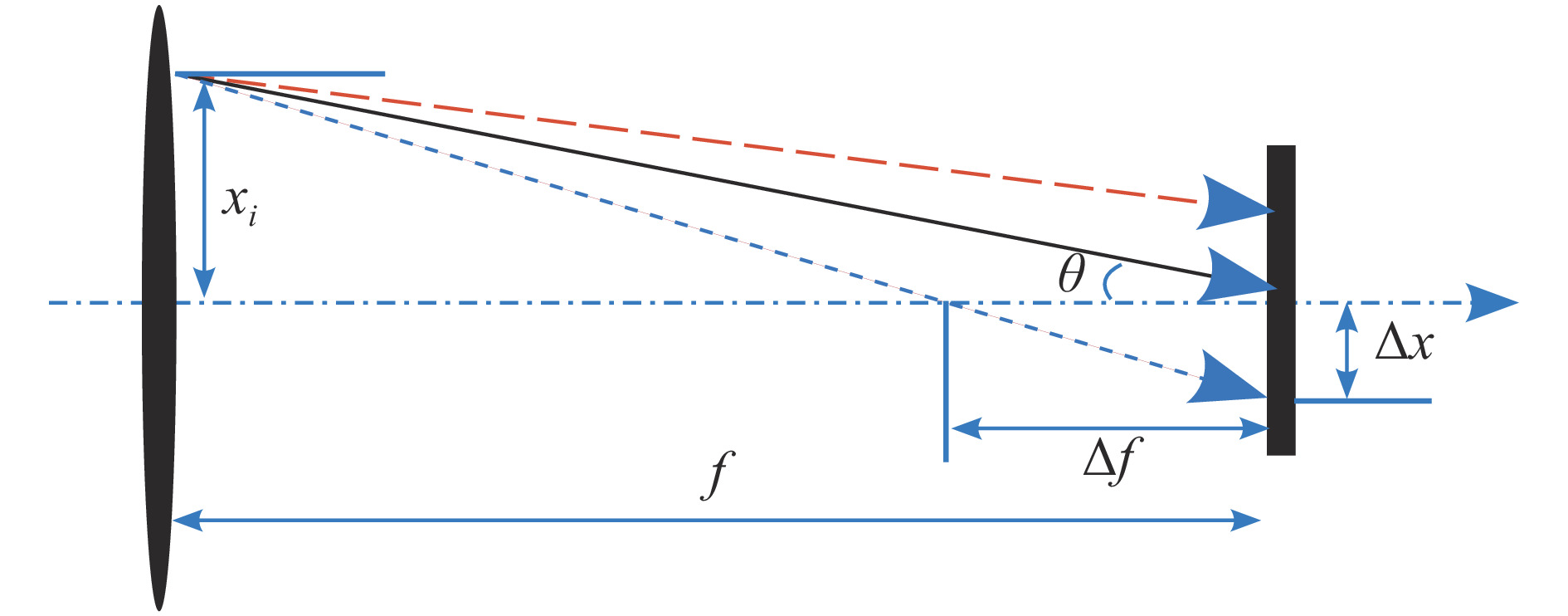
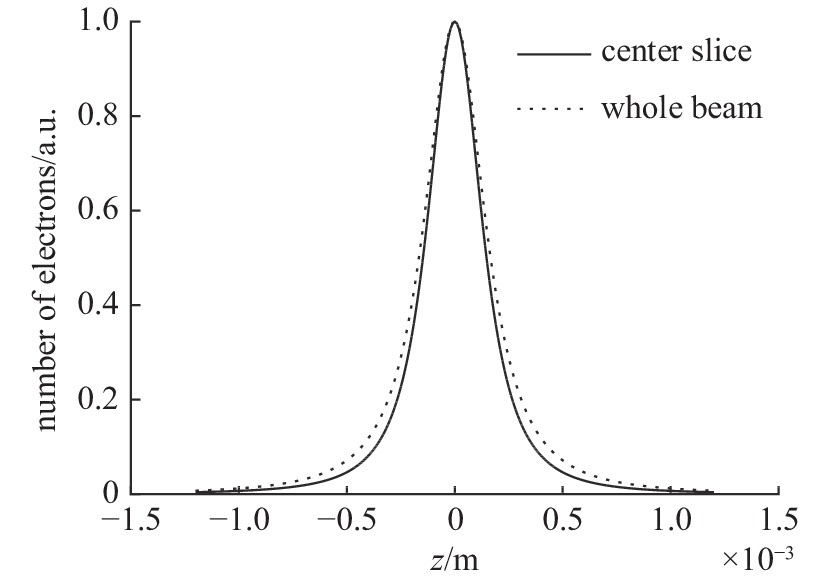
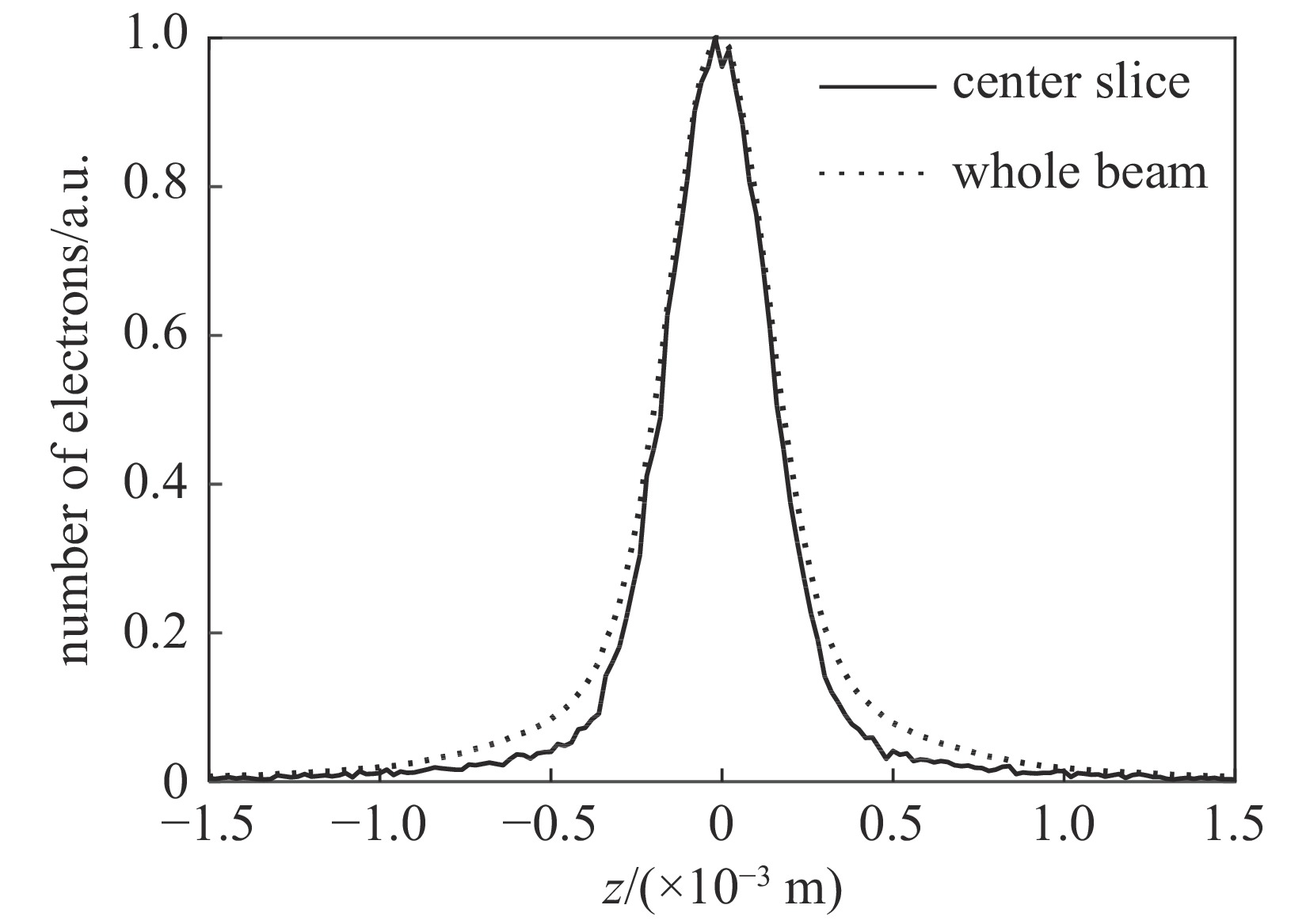
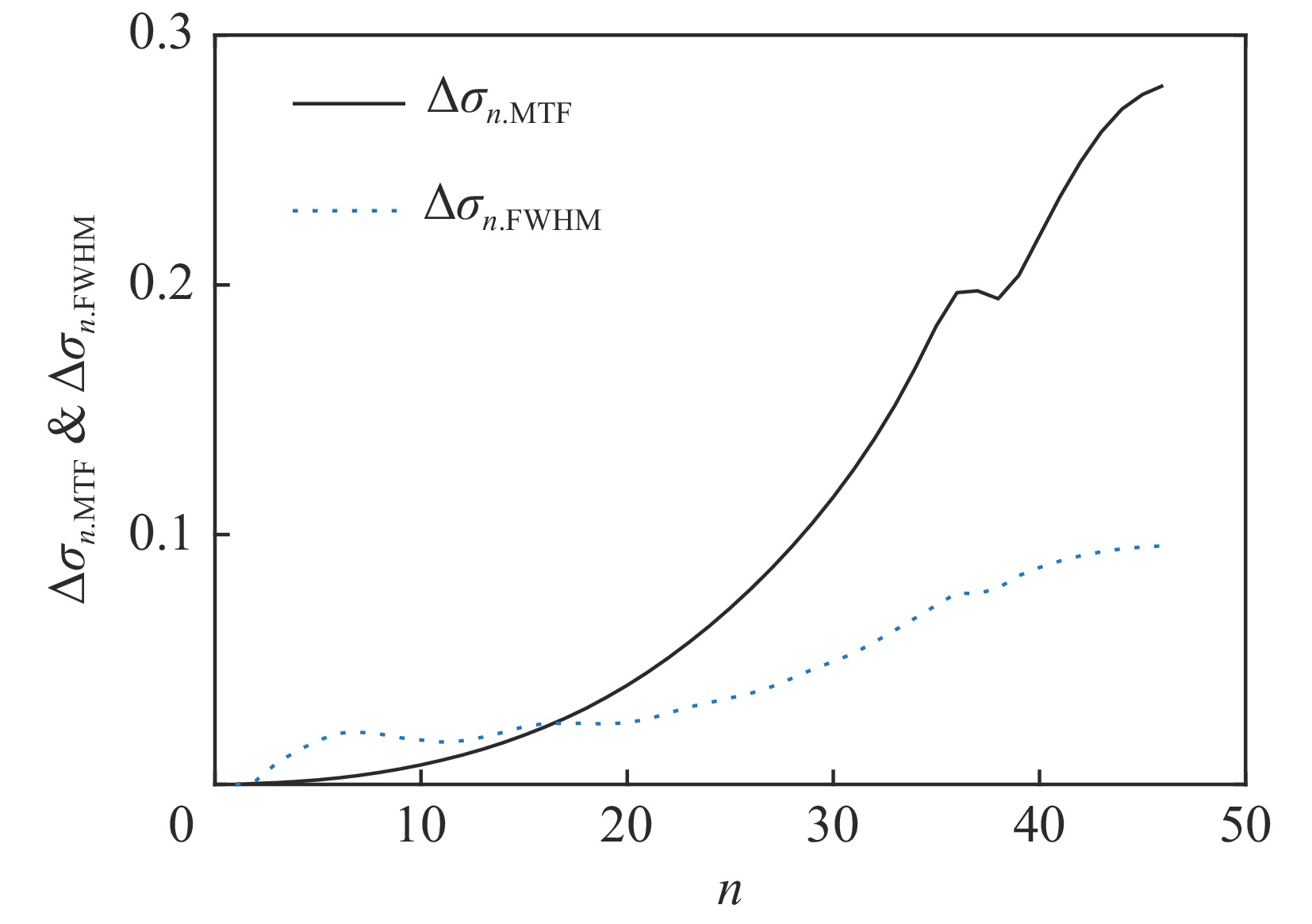
摘要: 介绍了均方根（RMS）、半高全宽（FWHM）和50%调制传递函数（MTF）等效均匀分布等焦斑尺寸评价方法。针对一台直线感应加速器，通过建立理论模型和开展逐束片PIC模拟研究了长脉冲（约100 ns）电子束的聚焦过程，分析了能量、流强与平顶区差异较大的脉冲上升/下降沿对FWHM和MTF焦斑尺寸的影响。研究结果表明：能散度较大的束流上升/下降沿会导致束流焦斑，尤其是MTF焦斑显著增长，在模拟结果中FWHM尺寸增长约9%，而MTF尺寸增长达到约24%，是目前导致束流底宽偏大的主要因素之一。Abstract: A brief introduction to evaluating the beam size with the Root-Mean-Square (RMS) value, the full-width-half-maximum (FWHM) value and the modulation-transfer-function (MTF) value is given in this paper. The focusing of the long pulse electron beam (～100 ns) in an induction linear accelerator is studied by both theoretical analysis and numerical simulation, the contribution of the energy and current difference of the rising edge and the falling edge to the final beam size are discussed. In our results, the rising edge and the falling edge of the beam with large energy deviation may lead to a significant increase of the beam size, especially the MTF beam size, i.e. the FWHM beam size is increased by about 9% while the MTF beam size is increased by about 24%.
-
Key words:
- linear induction accelerator /
- bunch size /
- energy spread /
- beam slice
-
图 1 均匀分布、高斯分布、本涅特分布曲线(a)，及对应的空间频域曲线F(k)(b)
Figure 1. The curvatures of Kapchiskij-Vladimirskij (KV) distribution, Gaussian distribution, Bennett distribution (a), and their spatial Fourier expansion (b)
图 2 焦距差异导致的束流横向位置差异示意图
Figure 2. The position deviation of electrons induced by focusing length difference
图 3 根据实验数据获得的束流的能量和流强分布
Figure 3. Current and energy distribution of the electron beam measured in experiment
图 4 根据公式（1）计算得到的中心束片和整个束流聚焦后的横向分布
Figure 4. Transverse profiles of the center slice and of the whole beam calculated with formula (1)
图 5 根据公式（1）计算得到第#(46−n) 至 #(46+n)号束片叠加后的MTF尺寸（右），其中#46为中心束片
Figure 5. MTF size of the electron bunch composed with slice #(46−n) to #(46+n) (right), the results are calculated with formula (1)
图 6 PIC模拟得到的中心束片和整个束流聚焦后的横向分布
Figure 6. Transverse profiles of the center slice and of the whole beam simulated with ASTRA
图 7 PIC模拟得到的第#(46−n) 至 #(46+n)号束片叠加后的MTF尺寸，其中#46为中心束片
Figure 7. MTF size of the electron bunch composed with slice #(46−n) to #(46+n) , the results are calculated with the PIC code ASTRA
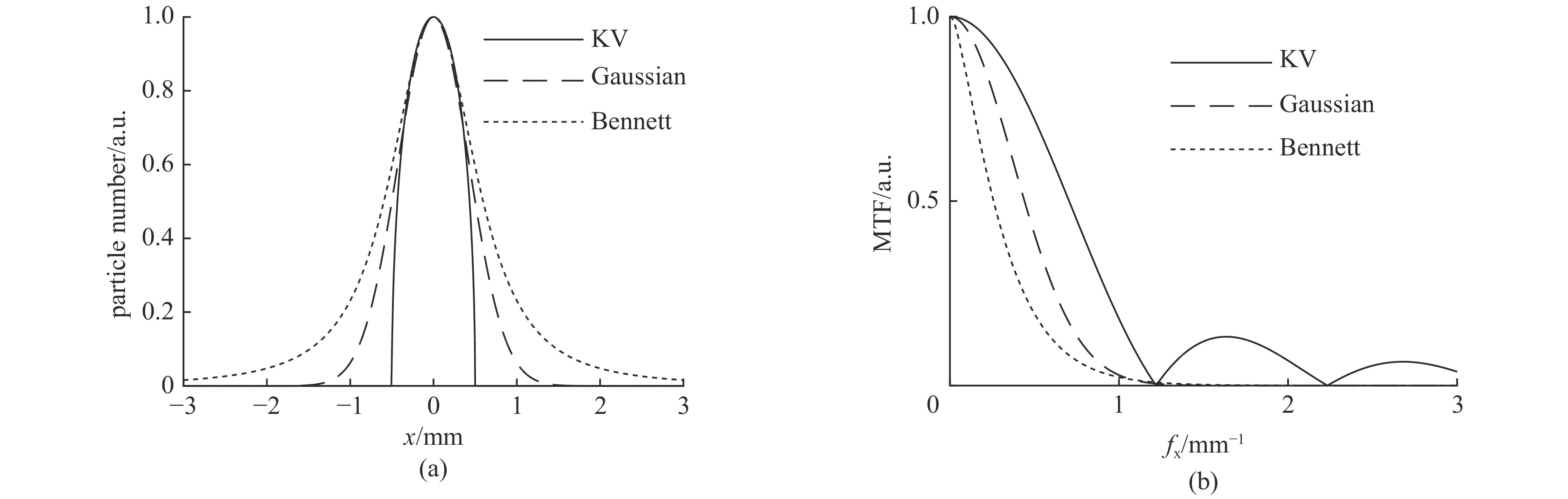
表 1 不同分布函数下，FWHM尺寸与MTF尺寸的对应关系
Table 1. Relationship between the FWHM beam size and the MTF beam size in various distributions
f(x) σFWHM/mm k0/mm−1 σMTF/mm KV 1.00 0.705 1.00 Gaussian 1.00 0.441 1.60 Bennett 1.00 0.258 2.70 
下载: 导出CSV
-
[1] 邓建军, 丁伯南, 王华岑, 等. “神龙一号”直线感应加速器物理设计[J]. 强激光与粒子束, 2003, 15(5):502-504. (Deng Jianjun, Ding Bo’nan, Wang Huacen, et al. Physical design of the Dragon-I linear induction accelerator[J]. High Power Laser and Particle Beams, 2003, 15(5): 502-504Deng Jianjun, Ding Bonan, Wang Huacen, et al. Physical design of the Dragon-I Linear induction accelerator[J]. High Power Laser and Particle Beams, 2003, 15(5): 502-504 [2] Klasky M L. Physics based radiography[R]. LA-CP-18-00890, 2018. [3] 石金水, 邓建军, 章林文, 等. 神龙二号加速器及其关键技术[J]. 强激光与粒子束, 2016, 28:010201. (Shi Jinshui, Deng Jianjun, Zhang Linwen, et al. Dragon-II accelerator and its key technology[J]. High Power Laser and Particle Beams, 2016, 28: 010201 doi: 10.11884/HPLPB201628.010201Shi Jinshui, Deng Jianjun, Zhang Linwen, et al. Dragon-II accelerator and its key technology[J]. High Power Laser and Particle Beams, 2016, 28: 010201 doi: 10.11884/HPLPB201628.010201 [4] Ekdahl C. Electron-beam dynamics for an advanced flash-radiography accelerator[J]. IEEE Transactions on Plasma Science, 2015, 43(12): 4123-4129. doi: 10.1109/TPS.2015.2496499 [5] 施将君. 高能闪光照相引论[M]. 绵阳: 中物院流体物理研究所科协, 1998Shi Jiangjun. Introduction of high-energy flash radiography[M]. Mianyang: Scientific Book Series of IFP, 1998 [6] Klasky M L. A correct flat field model for DARHT[R]. LA-UR-19-29164, 2019. [7] 王毅, 李勤, 刘云龙, 等. 用于直线感应加速器光源焦斑测量的双锥厚针孔结构设计[J]. 强激光与粒子束, 2019, 31:065102. (Wang Yi, Li Qin, Liu Yunlong, et al. Structure design of thick pinhole with double cones for spot size measurement of the linear induction accelerator light source[J]. High Power Laser and Particle Beams, 2019, 31: 065102 doi: 10.11884/HPLPB201931.180291Wang Yi, Li Qin, Liu Yunlong, et al. Structure design of thick pinhole with double cones for spot size measurement of the linear induction accelerator light source[J]. High Power Laser and Particle Beams, 2019, 31: 065102 doi: 10.11884/HPLPB201931.180291 [8] Wu Yuanhui, Chen Y J. ENSOLVE: A simulation code for FXR LIA downstream section[C]//Proceedings of the 9th International Particle Accelerator Conference. 2018: 2271-2273. [9] Ekdahl C. Characterizing flash-radiography source spots[J]. Journal of the Optical Society of America A, 2011, 28(12): 2501-2509. doi: 10.1364/JOSAA.28.002501 [10] 王毅, 李勤, 代志勇. 蒙特卡罗模拟分析电子束发射度对照射量空间分布影响[J]. 强激光与粒子束, 2017, 29:065006. (Wang Yi, Li Qin, Dai Zhiyong. Analysis on influence of beam emittance on spatial distribution of exposure using Monte Carlo simulation[J]. High Power Laser and Particle Beams, 2017, 29: 065006 doi: 10.11884/HPLPB201729.170029Wang Yi, Li Qin, Dai Zhiyong. Analysis on influence of beam emittance on spatial distribution of exposure using Monte Carlo simulation[J]. High Power Laser and Particle Beams, 2017, 29: 065006 doi: 10.11884/HPLPB201729.170029 [11] Pöplau G, van Rienen U, Flöettmann K. 3D space charge calculations for bunches in the tracking code Astra[C]//Proceedings of EPAC. 2006: 2203-2205. [12] Zhu Jun. Design study for generating sub-femtosecond to femtosecond electron bunches for advanced accelerator development at SINBAD[D]. Hamburg: Universität Hamburg, 2017. 期刊类型引用(1)
1. 顾余辉. 直线加速器维修维护及质控措施研究分析. 中国设备工程. 2024(07): 48-50 . 
百度学术其他类型引用(0)
-
点击查看大图
计量
- 文章访问数: 651
- HTML全文浏览量: 237
- PDF下载量: 45
- 被引次数: 1
