Intelligent optimization method for lead-bismuth reactor based on Kriging surrogate model
-
摘要: 铅铋反应堆广泛应用的需求要求研究人员在现有堆芯方案的基础上开展大量优化设计工作。针对铅铋反应堆多物理、多变量、多约束耦合影响的多维非线性约束优化设计问题，基于Kriging代理模型、正交拉丁超立方抽样和SEUMRE空间搜索技术构建铅铋反应堆智能优化方法，耦合物理蒙卡计算/热工分析程序，开发包含抽样、耦合程序前后处理、反应堆优化分析功能的优化平台，并以铅铋反应堆SPALLER-4，URANUS为原型分别开展最小燃料装载量的方案寻优与参数优化验证。验证结果表明，该智能优化方法用于铅铋反应堆设计方案寻优和堆芯参数优化可行、有效，相比传统蒙卡程序计算寻优，在保证预测精度前提下极大地降低了计算成本，与URANUS初始模型比较，燃料装载量、堆芯总质量、活性区体积、堆芯总体积分别优化10.8%，11.5%，18.1%，17.1%，为基于代理模型的智能优化方法应用于铅铋反应堆的优化设计提供参考。
-
关键词:
- 铅铋反应堆 /
- 智能优化 /
- Kriging代理模型 /
- SEUMRE空间搜索 /
- 正交拉丁超立方抽样
Abstract: The extensive application requirements of lead-bismuth reactors require researchers to carry out a lot of optimization design work on the basis of existing core schemes. Aiming at the multi-dimensional nonlinear constrained optimization design problem of lead-bismuth reactor with multi-physical, multi-variable and multi-constraint coupling effects, an intelligent optimization method for lead-bismuth reactor was constructed based on Kriging surrogate model, orthogonal Latin hypercube sampling and SEUMRE spatial search technology. Coupled with physical Monte Carlo calculation/thermal ranalysis code, an optimization platform including sampling, pre-and post-processing of coupling program and reactor optimization analysis function was developed. Taking SPALLER-4 and URANUS as prototypes, the scheme optimization and parameter optimization verification of minimum fuel load were carried out respectively. The verification results show that the core intelligent optimization method is feasible and effective for the optimization of lead-bismuth reactor design scheme and core parameters. Compared with the traditional Monte Carlo calculation optimization, the calculation cost is greatly reduced under the premise of ensuring the prediction accuracy. Compared with the URANUS initial model, the fuel loading, the total mass of the core, the volume of the active zone and the total volume of the core are optimized by 10.8%, 11.5%, 18.1% and 17.1% respectively, which provides a reference for the intelligent optimization method based on the surrogate model applied to the optimization design of lead-bismuth reactor. -
自福岛核电站事故发生以来，反应堆的安全性越来越受到公众的关注，成为影响核能发展的关键因素。采用非能动系统来提高反应堆的固有安全性已经在新的反应堆设计中得到了广泛的应用。其中，利用依靠回路内冷热段内冷却剂的密度差来产生驱动压头带走堆芯余热的自然循环成为主要的研究方向。目前，国际上对自然循环的研究以试验和数值模拟为主。试验研究方面，杨祖毛等[1]对单相自然循环进行了大量的试验，研究了稳态自然循环流量与热源功率、进出口温差的关系；黄彦平[2]通过试验研究了自然循环能力的影响因素等。但试验研究大多针对具体的回路及系统，不具有良好的移植性，且需要大量的资金投入。数值模拟方面，国内外通常使用一些系统分析程序，如RELAP5，RETRAN-02等大型商用软件，对于某些反应堆，也会采用独立开发的专用程序，如田文喜等[3]开发了CARR堆的自然循环能力计算程序，黄洪文等[4]开发了池式研究堆的自然循环能力分析程序，Kaminaga等[5]开发了JRR-3M自然循环能力程序。针对JRR-3M类型的研究堆，稳定自然循环形成前存在冷却剂流动方向反转的过程，有必要开展瞬态安全计算分析。本文利用RELAP5/Mod 3.4对JRR-3M进行了细致的堆芯建模，研究了不同事故条件下自然循环建立前的流量反转过程瞬态热工特性，并得到了瞬态时自然循环的载热极限，同时验证了计算模型和计算方法的可行性。
1. 计算模型
1.1 系统概述
RELAP程序是美国爱达荷国家工程实验室开发、美国核管理委员会批准的用于工程审评的大型瞬态热工水力计算程序，是一维瞬态、两流体六方程流体力学及点堆动力学模型[6]，现已广泛用于压水堆的事故模拟分析。JRR-3M是一座重水慢化、轻水冷却的池式研究堆，在正常运行工况下，冷却剂在两台主泵的驱动下从堆芯上部水池进入堆芯，向下流经堆芯带走裂变热后流入下部的下联箱，与换热器内二次侧的冷却水进行热交换冷却后重新流入主泵。在自然循环阶段，下联箱与水池连接的自然循环阀开启，池水在自然循环压头的驱动下进入下联箱，向上流过堆芯带走衰变热后返回水池，形成自然循环回路。应急冷却系统由两台由不间断电源供电的辅助泵组成，它们的额定流量为75.00 kg·s-1，最多能持续工作3 h。在发生场外电源丧失事故时，一台辅助泵投入运行，带走堆芯热量。
在一回路失去强迫流动后，存在一个由于冷却剂流动方向反转所导致的零流量时刻，此时由于没有冷却剂的流动带走衰变热，堆芯温度迅速上升，该时刻堆芯最有可能被烧毁。基于RELAP5/Mod 3.4程序，对JRR-3M进行建模，反应堆节点图如图 1所示。
其中，考虑到堆水池中存在明显的热分层现象以及内部循环，用两个管道(100，102)来模拟堆芯上部水池，两根管间用横向接管连接，最上方的控制体为空气层，时间控制体130表示空气的温度压力边界，取35 ℃和1.013×105 Pa。104和106是两种不同燃料组件的平均通道，108表示热通道，110和112表示旁路流道，堆芯流道均划分为15个控制体。114表示下联箱，116是环绕堆芯的水池，它们之间用自然循环阀连接。正常运行时从堆芯流出的冷却剂在热交换器118中与202中的冷却水进行冷却热交换。冷却剂由主泵流出后在分支部件126汇合后流回堆芯上部水池。
对于堆芯内功率的分布取该池式反应堆的物理设计结果，其功率衰变曲线采用中国行业标准EJ/T 745-2001[7]推荐公式计算给出, 即
P(τ0)=G(t)4∑i=1∫τ00Pi(t)Qif(t)dt (1) Q(t)=1.0+τ0.40φ(3.24×10−6+5.23×10−10t) (2) 式中：P(τ0)是τ0时刻的裂变总功率；G(t)是考虑裂变产物中子俘获的校正因子；Pi(t)是核素i在t时刻的裂变功率；Qi为核素i一次裂变可回收能量(MeV)；f(t)为可裂变核素的衰变热功率函数，它的值由标准附表给出(略)；φ为一个初始裂变原子的裂变数；i取1，2，3，4分别代表235U热中子裂变、239Pu热中子裂变、238U快中子裂变和241Pu热中子裂变对衰变热功率的贡献；t为停堆后时间(s)。
1.2 稳态参数
将系统调节至稳态工况是进行瞬态计算的前提条件。在自然循环的瞬态计算中，系统各个参数应在某个预计工况下稳态运行，随后关闭主泵打开自然循环阀进行瞬态计算，而这个稳态的工况就决定了事故的初始状态。通过调节回路内的物理参数，使得稳态工况下的热工参数与设计的热工参数一致且达到稳定。表 1为该池式研究堆的热工设计参数。
表 1 池式研究堆主要设计参数Table 1. Main design parameters of pool-type research reactortotal power/MW total mass flow rate/(kg·s-1) inlet temperature/℃ outlet temperature/℃ core inlet pressure/MPa 20.00 661.91 35.00 42.19 1.69 1.3 安全准则
按照该堆设计确定的安全标准为：
(1) 使用Sudo临界热流密度经验公式[8]，计算的最小偏离泡核沸腾比(MDNBR)应大于限值1.5。
(2) 燃料元件芯体最高温度低于250 ℃。
2. 计算结果与分析
2.1 无应急冷却的场外电源丧失事故分析
反应堆在满功率正常运行了100 s后发生外电源丧失事故，主泵由于失去电力供应立即失电惰转，二次侧热阱立即丧失，自然循环阀打开，1 s后控制棒落下反应堆进行停堆，此时堆芯所产生的热量主要依靠主泵惰转和自然循环带走。整个过程的事件序列列于表 2。
表 2 无应急冷却系统事件序列Table 2. Accident process without emergency cooling systemevent start time event start time main pump loss of off-site power supply 100 s control rods drop 101 s secondary side loss of hot trap 100 s finish main pump coasting 220 s open the natural circulation valve 100 s reverse coolant flow 221 s 图 2为事故分析的结果曲线。
从图 2(a)和图 2(b)中可以看出，在0~100 s内，反应堆满功率稳态运行，堆芯流量保持不变。在100 s时刻，由于主泵失电惰转流量迅速减少，在t=220 s时主泵惰转停止，堆芯流量减少至0。此时自然循环阀已经打开，在自然循环驱动压头的作用下，由于热通道中热流密度最大，故最先产生流量反转，随后堆芯流量反转，冷却剂由下而上地通过堆芯，自然循环迅速建立。
从图 2(c)看出，在稳态运行时，燃料芯块最热温度为108.27 ℃，包壳最高温度为99.37 ℃, 在101 s时控制棒开始下落后，由于堆芯功率的呈指数式降低，燃料板和冷却剂的温度也随之急剧下降。随后，由于冷却剂流量不足以完全带走燃料所产生的热量，热构件和冷却剂的温度逐渐上升。在220 s时冷却剂流量为0，燃料外表面与冷却剂的对流换热性能最差，燃料板的温度达到峰值，燃料芯块的峰值温度为114.30 ℃, 包壳峰值温度为114.07 ℃。此后，由于自然循环流量的增大，对流换热作用增强，燃料板和冷却剂的温度开始下降。在稳定的自然循环建立后，燃料板和冷却剂的温度由于堆芯功率的缓慢衰减而缓慢降低。
图 2(d)是整个过程中的MDNBR变化曲线。从图中可以看出，热管处的MDNBR在稳态运行时为2.66，在反应堆停堆后由于燃料板热流密度的急剧减少而迅速增加，随后随着流量的降低而降低，在流量反转时刻为最小值，最小值为0.31，远低于安全限值1.50。
2.2 有应急冷却的场外电源丧失事故分析
当该池式研究堆在满功率正常运行了100 s后发生外电源丧失事故，主泵失电惰转，当冷却剂流量低于75.00 kg·s-1时，一台辅助泵投入运行。当t=3 188 s时，衰变功率已降至200 kW，辅助泵停止运行，在辅助泵停止运行前5 s打开自然循环阀。事故过程中的事件时间序列如表 3所示。
表 3 有应急冷却事件序列Table 3. Accident process with emergency cooling systemevent start time event start time main pump loss of off-site power supply 100 s close auxiliary pump 3 188 s control rods drop 101 s auxiliary pump finish coast 3 198 s input auxiliary pump 110 s coolant flow reverse 3 199 s open the natural circulation valve 3 183 s 图 3为事故分析的结果曲线。
从图 3(a)和图 3(b)中可以看出，在100 s以前，反应堆满功率稳态运行，堆芯流量不变。100 s后主泵失电惰转，流量降低。当流量降低至75.00 kg·s-1时，辅助泵投入运行，堆芯流量保持不变。当t=3 183 s时，自然循环阀打开，从图中可以发现堆芯流量平台有一个下降。这时由于此时堆水池与反应堆一回路连接，具有了一定的流量，导致流过堆芯的流量减少。在t=3 188 s时关闭辅助泵，堆芯流量逐渐降低至0，随后由于自然循环的建立，流量发生反转，最后趋向稳定。
通过比较图 2(c)和图 3(c)可以发现，在投入应急冷却系统的事故工况下，由于堆芯拥有一定程度的强迫流量，这一部分的流量带走了部分衰变热，有效地降低了燃料板及冷却剂的温度，相较于未投入应急冷却系统的条件下，燃料芯块峰值温度降低了46.10 ℃，堆芯材料不会发生熔毁。同时可以发现冷却剂的温度和燃料板温度的变化趋势相似，但有一定的滞后。
从图 3(d)可以看出，有应急冷却时事故过程中的MDNBR始终大于安全限值，不会发生偏离核态沸腾，池式研究堆始终处于安全状态。
2.3 最大载热能力计算
为进一步探究池式研究堆自然循环瞬态过程中的最大载热能力，在堆芯功率衰减至不同功率水平时关闭辅助泵并打开自然循环阀，不同功率下自然循环过程中的最高燃料温度和MDNBR如图 4所示。
从图 4可以明显看出，此时反应堆的安全性主要受到来自MDNBR的限制，因此，池式研究堆最大瞬态自然循环能力约为590 kW。
3. 结论
本文利用系统性分析程序RELAP5/Mod 3.4对JRR-3M池式研究堆进行了建模，计算了在无应急冷却和有应急冷却情况下的丧失场外电源事故。RELAP5很好地模拟了堆芯流量的反转过程以及自然循环的建立过程。针对这两种事故工况，计算得到了堆芯各个流道的温度、压力、冷却剂流量等热工水力参数。计算结果表明：若未投入应急冷却系统，反应堆在失去场外电源后热管内MDNBR为0.31，小于1.5的安全限值，会发生偏离核态沸腾，存在烧毁堆芯的风险。应急冷却系统能有效地降低事故后燃料板及冷却剂的温度，提高了系统的安全性。在瞬态条件下，池式研究堆的最大自然循环能力为590 kW，大于设计值200 kW，表明该堆具有良好的固有安全性。
-
图 1 堆芯智能优化方法主要技术原理
Figure 1. Main technical principle of core intelligent optimization method
图 7 Kriging代理模型预测Keff、燃耗与蒙卡程序RMC计算值对比图
Figure 7. Comparison of Keff, burnup predicted by Kriging surrogate model and RMC calculated value
图 8 SPALLER-4燃料装载量寻优迭代图
Figure 8. Iterative graph of fuel loading optimization for SPALLER-4
图 9 Kriging代理模型预测Keff、燃耗与蒙卡程序RMC计算值对比图
Figure 9. Comparison of Keff, burnup predicted by Kriging surrogate model and RMC calculated value
图 10 URANUS燃料装载量寻优迭代图
Figure 10. Iterative graph of fuel loading optimization for URANUS
表 1 Kriging代理模型常用相关函数及其表达式
Table 1. Commonly used related functions of Kriging surrogate model and their expressions
correlation function expression exponential function Rk(θk,dk)=exp(−θkdk) Gaussian function Rk(θk,dk)=exp(−θkd2k) linear function Rk(θk,dk)=max{0,1−θkdk} cubic spline function Rk(θk,dk)={1−15ζk+30ζ3k,0⩽ζk⩽0.21.25(1−15ζk)3,0.2<ζk<10,ζk⩾1,ζk=θkdk 
下载: 导出CSV
表 2 SPALLER-4设计参数及其材料与优化变量取值区间
Table 2. Materials used for the design parameters of SPALLER-4 and the interval value of optimization variables
design
schemethermal
power/MWfuel
loading/kgequivalent
diameter
of active
region/cmheight of
active
area/cmaverage volume
power density
of active
region/(W·cm−3)fuel (mass
fraction
of Pu)/%coolant
and
reflectorshielding
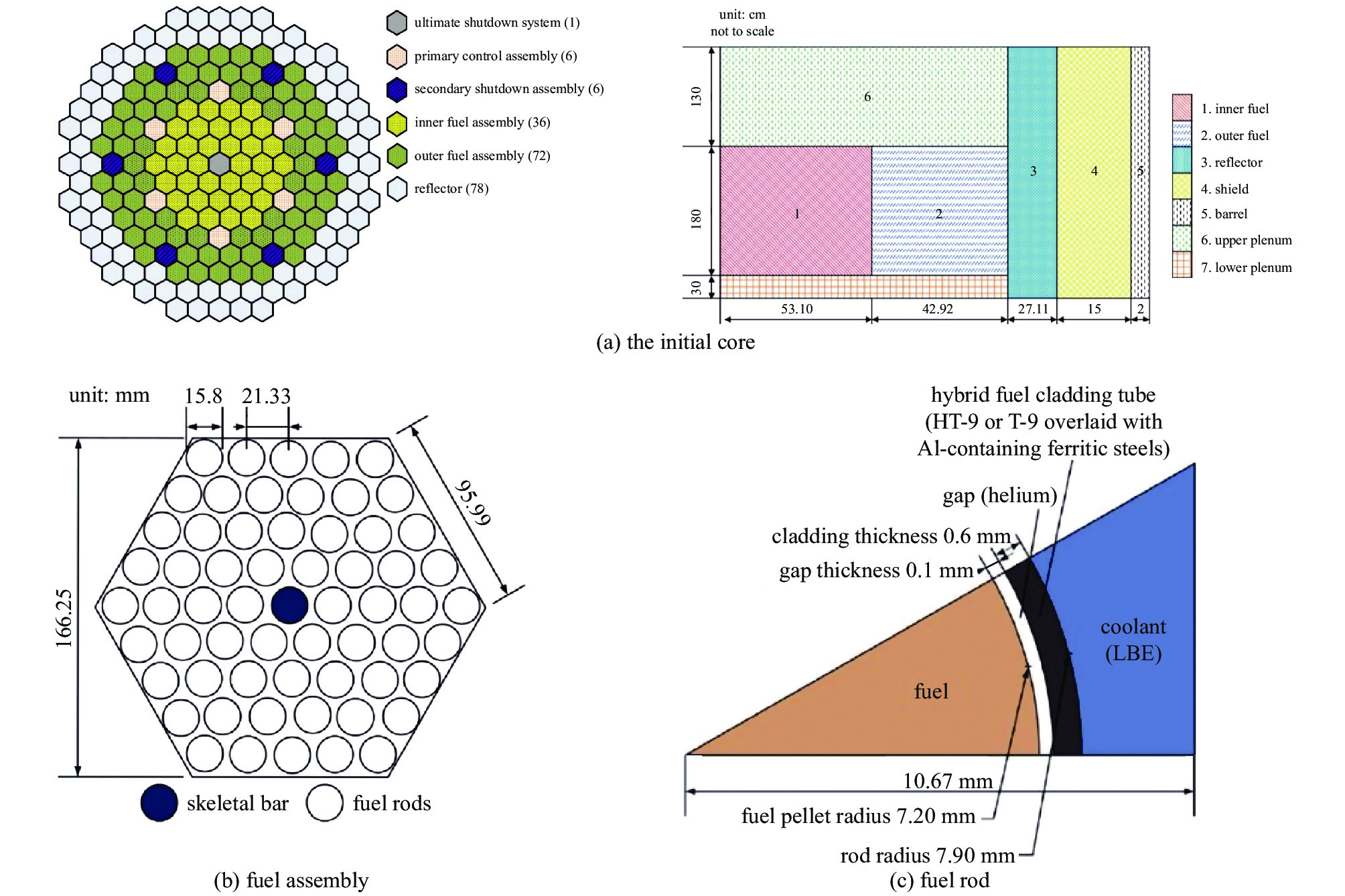
layerSPALLER-4 4 577.89 95.4 80 6.99 PuN-ThN (31/48) 208Pb-Bi(90) B4C(126) URANUS 100 17580 97.02 180 19.18 UO2(9.55/17.09) 208Pb-Bi(27.11 cm) B4C(15 cm) design
schemesolid
moderator
(thickness/cm)gate
diameter
ratiofuel rod
core
radius/cmair gap
of fuel rod
(thickness/cm)cladding of
fuel rod
(thickness/cm)upper/lower
end plug
of fuel
rod (height/cm)gas cavity/
spring area
of fuel rod
(height/cm)top/bottom
insulation
of fuel
rod (height/cm)SPALLER-4 BeO (3.5) 1.20 0.60 He (0.015) TH-9(0.06) TH-9(3/3) He(48/14) He(1/1) URANUS — 1.35 0.72 He (0.010) TH-9(0.06) TH-9(30/30) He(130/30) —
下载: 导出CSV
表 3 Kriging代理模型预测Keff、燃耗的精度验证结果
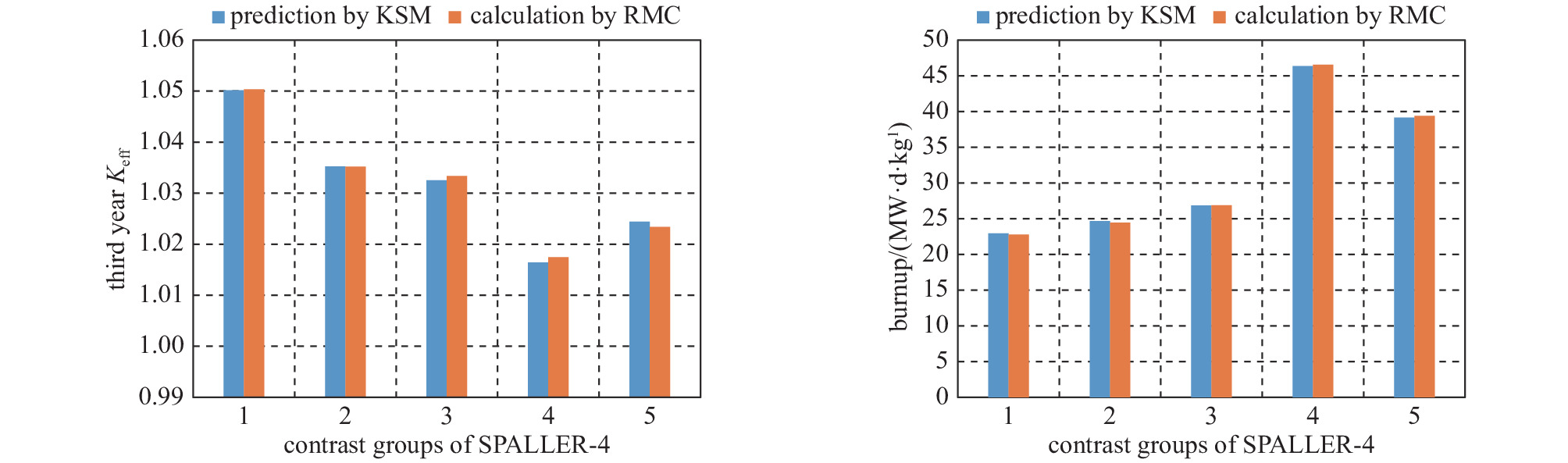
Table 3. Accuracy verification results of Kriging surrogate model for predicting Keff and burnup
contrast
groupthickness
of solid
moderator/cmmass fraction
of Pu in
fuel/%fuel rod
core
radius/cmheight of
core active
zone/cmgrid
diameter
ratiothird-year Keff burnup/(MW·d·kg−1) prediction
by KSMcalculation
by RMCrelative
error/%prediction
by KSMcalculation
by RMCrelative
error/%1 4.6555 47.2024 0.2911 112.1659 1.3710 1.0502 1.0503 −0.0154 22.9477 22.7960 0.6654 2 4.8222 45.4101 0.2776 115.2353 1.3773 1.0352 1.0352 0.0006 24.6610 24.4460 0.8794 3 4.9908 48.9315 0.2608 118.1860 1.4117 1.0325 1.0334 −0.0846 26.8646 26.8940 0.1093 4 4.5899 48.8228 0.2117 103.6606 1.3534 1.0164 1.0174 −0.0987 46.3528 46.5440 0.4108 5 4.7828 46.6647 0.2173 116.5918 1.3548 1.0244 1.0234 0.0994 39.1589 39.3960 0.6019
下载: 导出CSV
表 4 SPALLER-4堆芯设计方案寻优结果
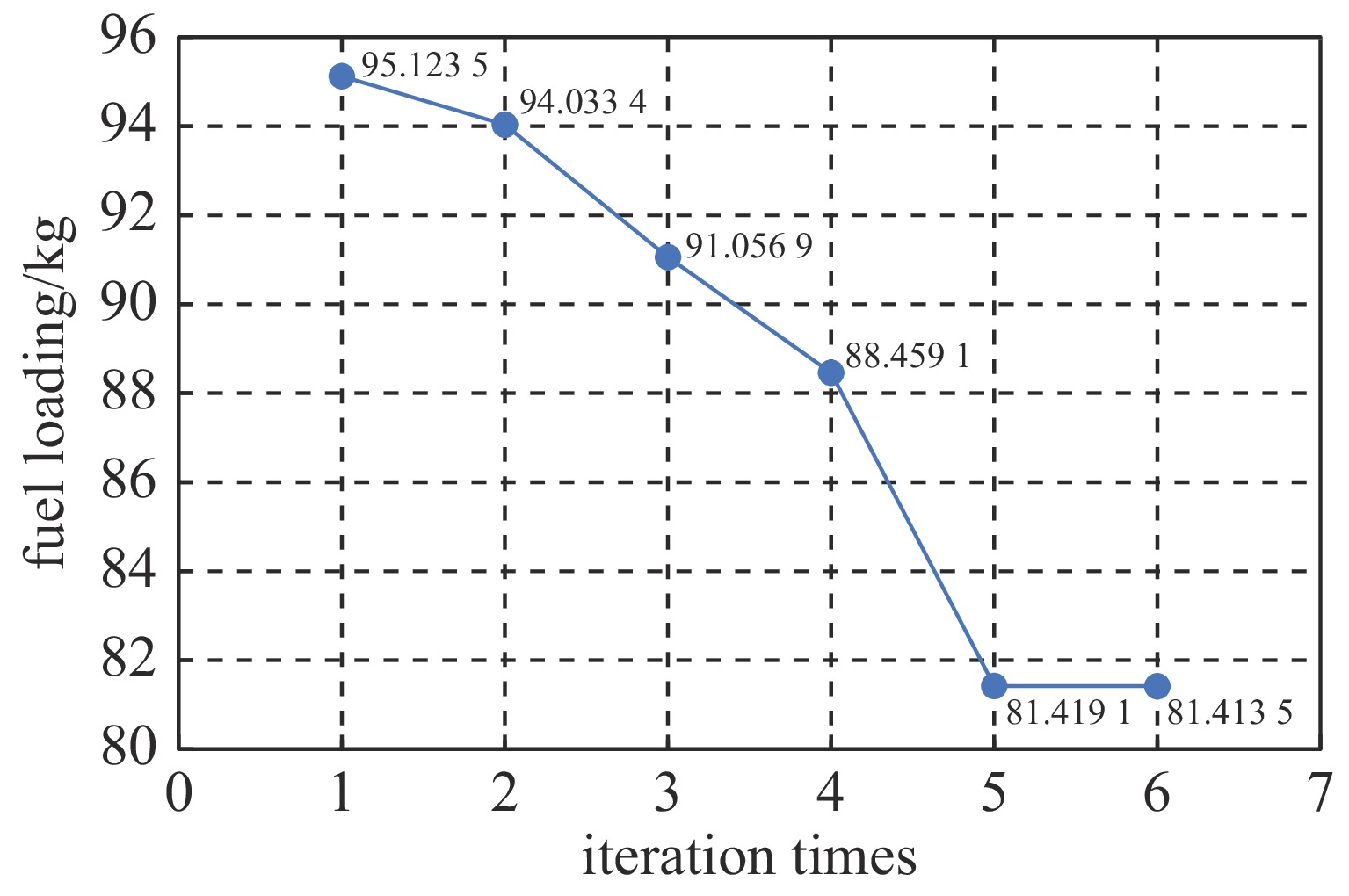
Table 4. Optimization results of SPALLER-4 core design scheme
thickness
of solid
moderator/cmmass fraction
of Pu in
fuel/%fuel rod
core
radius/cmheight of
core active
zone/cmgrid
diameter
ratiothird-year Keff burnup/(MW·d·kg−1) prediction
by KSMcalculation
by RMCrelative
error/%prediction
by KSMcalculation
by RMCrelative
error/%4.5732 49.8686 0.2003 100.0818 1.3131 1.0057 1.0052 0.0550 53.7021 53.7990 −0.0018
下载: 导出CSV
表 5 Kriging代理模型预测Keff、燃耗的精度验证结果
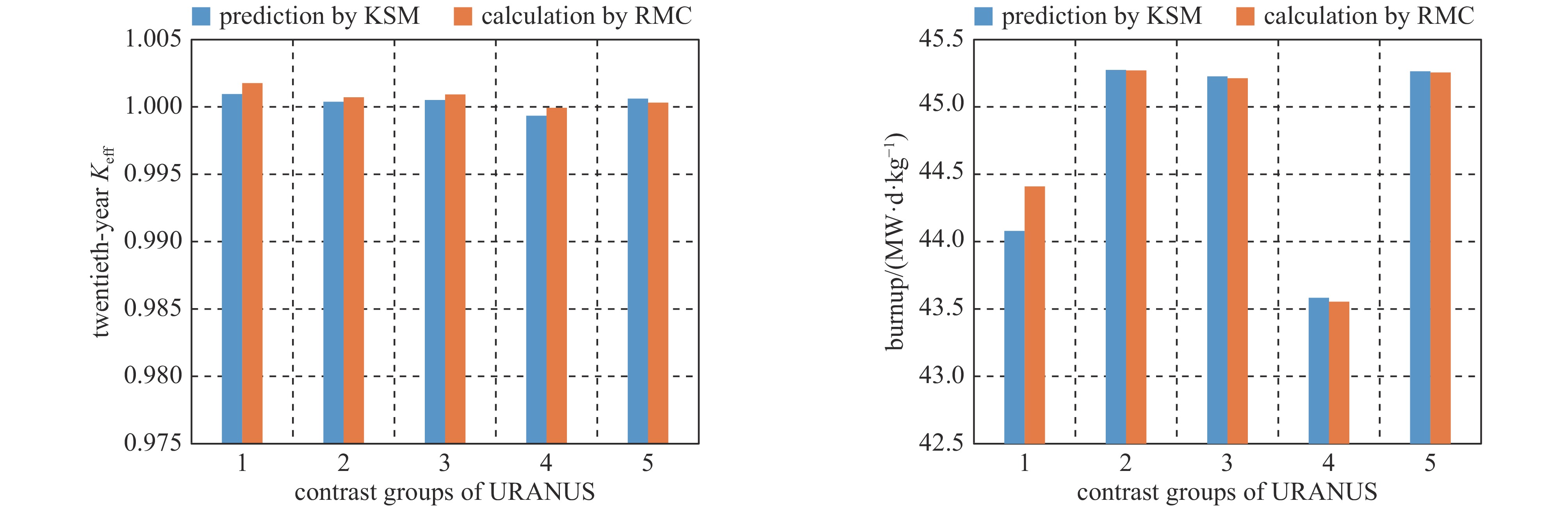
Table 5. Accuracy verification results of Kriging surrogate model for predicting Keff and burnup
contrast
groupfuel rod
core
radius/cmheight of
core active
zone/cmgrid diameter
ratiotwentieth-year Keff burnup/(MW·d·kg−1) prediction
by KSMcalculation
by RMCrelative
error/%prediction
by KSMcalculation
by RMCrelative
error/%1 0.7287 164.3119 1.3207 1.0010 1.0018 −0.0809 44.0797 44.4100 −0.7438 2 0.7373 157.4453 1.3208 1.0004 1.0007 −0.0338 45.2746 45.2710 0.0080 3 0.7388 156.9933 1.3211 1.0005 1.0009 −0.0409 45.2266 45.2130 0.0301 4 0.7410 153.9331 1.3205 0.9994 0.9999 −0.0585 43.5830 43.5540 0.0666 5 0.7374 157.4387 1.3203 1.0006 1.0003 0.0297 45.2645 45.2560 0.0187
下载: 导出CSV
表 6 URANUS堆芯设计参数优化结果
Table 6. Optimization results of design parameters for URANUS core
URANUS
corefuel rod
core
radius/cmheight of
core active
zone/cmgrid
diameter
ratioinitial
Kefftwentieth-year Keff burnup/(MW·d·kg−1) prediction
by KSMcalculation
by RMCrelative
error/%prediction
by KSMcalculation
by RMCrelative
error/%initial 0.7200 180.0000 1.3500 1.0289 — 1.0031 — — 41.5240 — optimization 0.7314 155.5838 1.2893 1.0307 1.0007 1.0010 −0.0229 46.5773 46.5530 0.0523
下载: 导出CSV
URANUS
corerefueling
interval/
EFPYfuel
loading/kgtotal mass
of core
(including
reflector)/kgvolume of
the active
area/m3average volume
power density
of the active
area/(W·cm−3)total volume
of core
(including
reflector)/m3maximum
temperature
of fuel
cladding/Kmaximum
temperature
of fuel
core/Kinitial 20 17580.0925 175459.3633 5.2138 19.1800 8.5734 600.6219 770.3892 optimization 20 15681.0697 155309.9496 4.2697 23.4208 7.1059 604.1702 796.0589
下载: 导出CSV
-
[1] 王建强, 戴志敏, 徐洪杰. 核能综合利用研究现状与展望[J]. 中国科学院院刊, 2019, 34(4):460-468. (Wang Jianqiang, Dai Zhimin, Xu Hongjie. Research status and prospect of comprehensive utilization of nuclear energy[J]. Bulletin of the Chinese Academy of Sciences, 2019, 34(4): 460-468 [2] 吴宜灿. 铅基反应堆研究进展与应用前景[J]. 现代物理知识, 2018, 30(4):35-39. (Wu Yican. Research progress and application prospects of lead-based reactors[J]. Modern Physics, 2018, 30(4): 35-39 [3] Zameer A, Mirza S M, Mirza N M. Core loading pattern optimization of a typical two-loop 300 MWe PWR using Simulated Annealing (SA), novel crossover Genetic Algorithms (GA) and hybrid GA(SA) schemes[J]. Annals of Nuclear Energy, 2014, 65: 122-131. doi: 10.1016/j.anucene.2013.10.024 [4] de Moura Meneses A A, Machado M D, Schirru R. Particle Swarm Optimization applied to the nuclear reload problem of a Pressurized Water Reactor[J]. Progress in Nuclear Energy, 2009, 51(2): 319-326. doi: 10.1016/j.pnucene.2008.07.002 [5] Khoshahval F, Minuchehr H, Zolfaghari A. Performance evaluation of PSO and GA in PWR core loading pattern optimization[J]. Nuclear Engineering and Design, 2011, 241(3): 799-808. doi: 10.1016/j.nucengdes.2010.12.023 [6] 王成. 新型优化算法开发及其在核动力装置优化中的应用[D]. 哈尔滨: 哈尔滨工程大学, 2018Wang Cheng. The development of new optimization algorithms and applications in optimal design for nuclear power plant[D]. Harbin: Harbin Engineering University, 2018 [7] 张扬. 多参数非线性系统全局敏感性分析与动态代理模型研究[D]. 长沙: 湖南大学, 2014Zhang Yang. The study on global sensitivity analysis and dynamic metamodel of multiple-parameters nonlinear system[D]. Changsha: Hunan University, 2014 [8] Kempf S, Forget B, Hu Linwen. Kriging-based algorithm for nuclear reactor neutronic design optimization[J]. Nuclear Engineering and Design, 2012, 247: 248-253. doi: 10.1016/j.nucengdes.2012.03.001 [9] Zeng Kaiyue, Stauff N E, Hou J, et al. Development of multi-objective core optimization framework and application to sodium-cooled fast test reactors[J]. Progress in Nuclear Energy, 2020, 120: 103184. doi: 10.1016/j.pnucene.2019.103184 [10] Kim K Y, Lee S M. Shape optimization of inlet plenum in a PBMR-type gas-cooled nuclear reactor[J]. Journal of Nuclear Science and Technology, 2009, 46(7): 649-652. doi: 10.1080/18811248.2007.9711571 [11] 李淞, 杨红义, 周志伟, 等. 基于克里金方法的快堆燃料组件设计[J]. 原子能科学技术, 2018, 52(7):1288-1293. (Li Song, Yang Hongyi, Zhou Zhiwei, et al. Design of fast reactor fuel assembly based on Kriging method[J]. Atomic Energy Science and Technology, 2018, 52(7): 1288-1293 doi: 10.7538/yzk.2017.youxian.0650 [12] Pebesma E J, Heuvelink G B M. Latin hypercube sampling of Gaussian random fields[J]. Technometrics, 1999, 41(4): 303-312. doi: 10.1080/00401706.1999.10485930 [13] Jin R, Chen W, Simpson T W. Comparative studies of metamodelling techniques under multiple modelling criteria[J]. Structural and Multidisciplinary Optimization, 2001, 23(1): 1-13. doi: 10.1007/s00158-001-0160-4 [14] 毛凤山, 陈昌富, 朱世民. 代理模型方法及其在岩土工程中的应用综述[J]. 地基处理, 2020, 2(4):295-306. (Mao Fengshan, Chen Changfu, Zhu Shimin. Surrogate model method and its application in geotechnical engineering[J]. Journal of Ground Improvement, 2020, 2(4): 295-306 [15] Younis A, Dong Zuomin. Metamodelling and search using space exploration and unimodal region elimination for design optimization[J]. Engineering Optimization, 2010, 42(6): 517-533. doi: 10.1080/03052150903325540 [16] Wang Kan, Li Zeguang, She Ding, et al. RMC – A Monte Carlo code for reactor core analysis[J]. Annals of Nuclear Energy, 2015, 82: 121-129. doi: 10.1016/j.anucene.2014.08.048 [17] Zhao Pengcheng, Liu Zijing, Yu Tao, et al. Code development on steady-state thermal-hydraulic for small modular natural circulation lead-based fast reactor[J]. Nuclear Engineering and Technology, 2020, 52(12): 2789-2802. doi: 10.1016/j.net.2020.05.023 [18] 赵鹏程. 小型自然循环铅冷快堆SNCLFR-100一回路主冷却系统热工安全分析[D]. 合肥: 中国科学技术大学, 2017Zhao Pengcheng. Thermal-hydraulic safety analysis of primary cooling system for small modular natural circulation LFR SNCLFR-100[D]. Hefei: University of Science and Technology of China, 2017 [19] 刘紫静, 赵鹏程, 张斌, 等. 超长寿命小型自然循环铅铋快堆堆芯概念设计研究[J]. 原子能科学技术, 2020, 54(7):1254-1265. (Liu Zijing, Zhao Pengcheng, Zhang Bin, et al. Research on core concept design of ultra-long life small natural circulation lead-based fast reactor[J]. Atomic Energy Science and Technology, 2020, 54(7): 1254-1265 doi: 10.7538/yzk.2019.youxian.0720 [20] 刘紫静, 赵鹏程, 任广益, 等. 长寿命小型自然循环铅基快堆燃料选型[J]. 原子能科学技术, 2020, 54(5):944-953. (Liu Zijing, Zhao Pengcheng, Ren Guangyi, et al. Fuel selection of long life small natural circulation lead-based fast reactor[J]. Atomic Energy Science and Technology, 2020, 54(5): 944-953 doi: 10.7538/yzk.2019.youxian.0402 [21] Jooeun Lee. Conceptual neutronic design of inverted core for lead-bismuth cooled small modular reactor[D]. Seoul: Graduate School of Seoul National University, 2017. [22] Kwak J, Kim H R. Development of innovative reactor-integrated coolant system design concept for a small modular lead fast reactor[J]. International Journal of Energy Research, 2018, 42(13): 4197-4205. doi: 10.1002/er.4177 [23] Shin Y H, Choi S, Cho J, et al. Advanced passive design of small modular reactor cooled by heavy liquid metal natural circulation[J]. Progress in Nuclear Energy, 2015, 83: 433-442. doi: 10.1016/j.pnucene.2015.01.002 [24] Shin Y H, Choi S, Cho J, et al. ICONE23-2135 design status of small modular reactor cooled by lead-bismuth eutectic natural circulation: Uranus[C]//Proceedings of ICONE-23 23rd International Conference on Nuclear Engineering. Chiba, Japan: 2015. [25] Driscoll N J, Hejzlar P. Reactor physics challenges in Gen-IV reactor design[J]. Nuclear Engineering and Technology, 2005, 37(1): 1-10. [26] Zhang Yan, Wang Chenglong, Lan Zhike, et al. Review of thermal-hydraulic issues and studies of lead-based fast reactors[J]. Renewable and Sustainable Energy Reviews, 2020, 120: 109625. doi: 10.1016/j.rser.2019.109625 [27] Grasso G, Petrovich C, Mattioli D, et al. The core design of ALFRED, a demonstrator for the European lead-cooled reactors[J]. Nuclear Engineering and Design, 2014, 278: 287-301. doi: 10.1016/j.nucengdes.2014.07.032 [28] Wallenius J, Suvdantsetseg E, Fokau A. ELECTRA: European lead-cooled training reactor[J]. Nuclear Technology, 2012, 177(3): 303-313. doi: 10.13182/NT12-A13477 [29] 杨红义, 过明亮. 中国实验快堆的设计创新与实现[J]. 原子能科学技术, 2020, 54(S1):199-205. (Yang Hongyi, Guo Mingliang. Design innovation and fulfillment of China experimental fast reactor[J]. Atomic Energy Science and Technology, 2020, 54(S1): 199-205 期刊类型引用(3)
1. 刘紫静，赵鹏程，李琼. 微型铅铋反应堆小型化与轻量化设计优化方法研究. 原子能科学技术. 2024(11): 2299-2309 . 
百度学术2. 王军健，李华鑫，李红菊，郑文健，闾川阳，马英鹤，任森栋，包士毅，贺艳明，杨建国. 静态腐蚀条件下铁素体/马氏体钢和奥氏体不锈钢与液态铅铋合金相容性研究进展. 强激光与粒子束. 2023(05): 138-149 . 本站查看3. 张家川，徐志刚，王军义，杨啸，王元钰，侯赓舜，董祺成. 固体火箭发动机对接装配密封圈应力在线预测方法. 固体火箭技术. 2023(02): 287-296 . 百度学术其他类型引用(4)
-
下载:
点击查看大图
计量
- 文章访问数: 936
- HTML全文浏览量: 410
- PDF下载量: 64
- 被引次数: 7
