Prediction of coupling cross section of hexagonal aperture array based on BP neural network
-
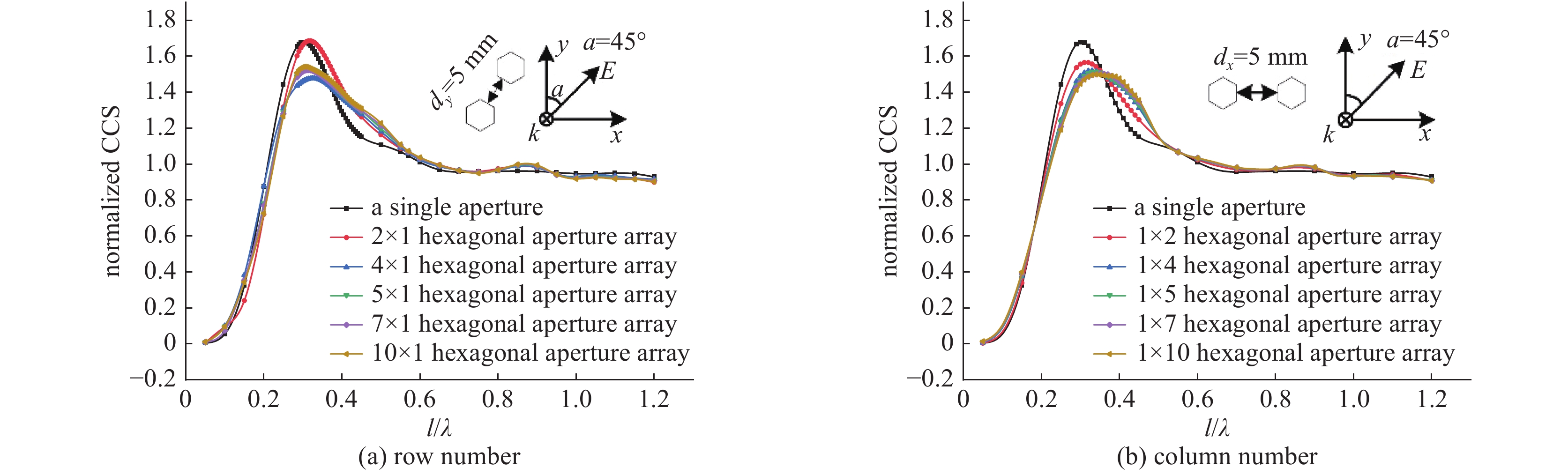
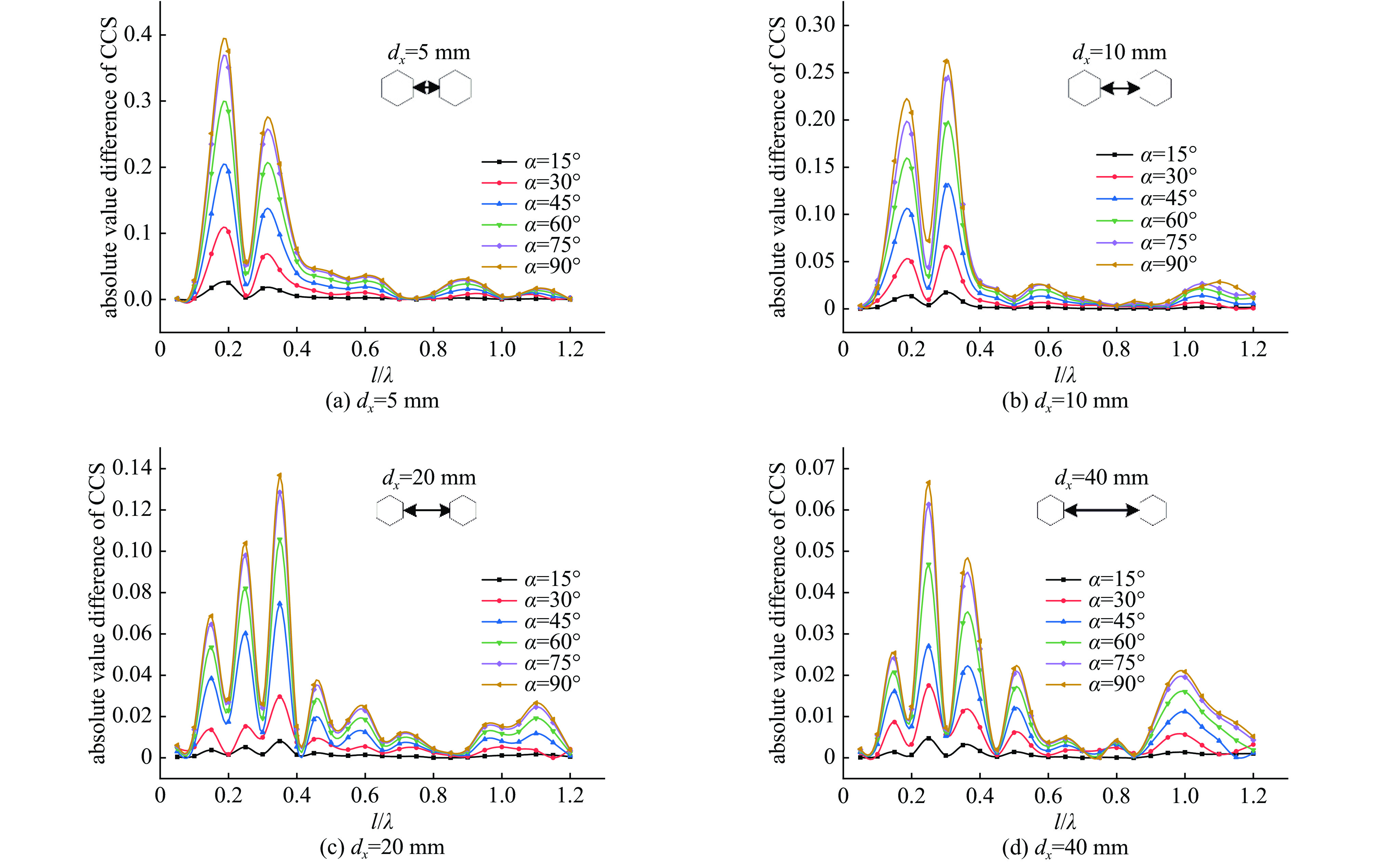
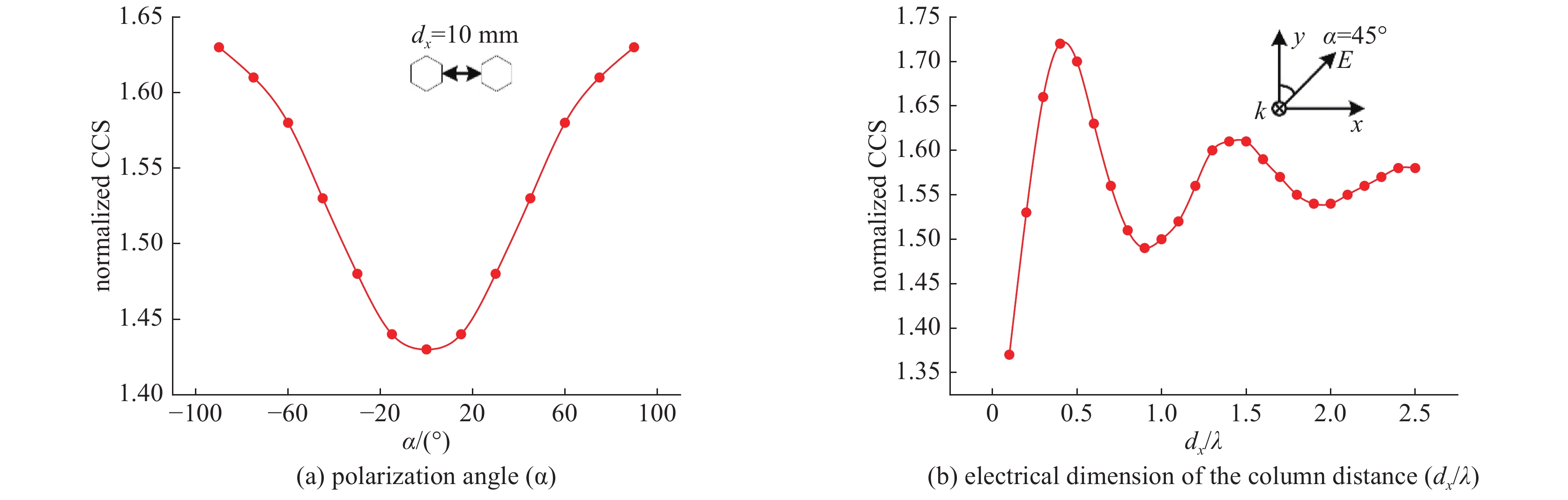
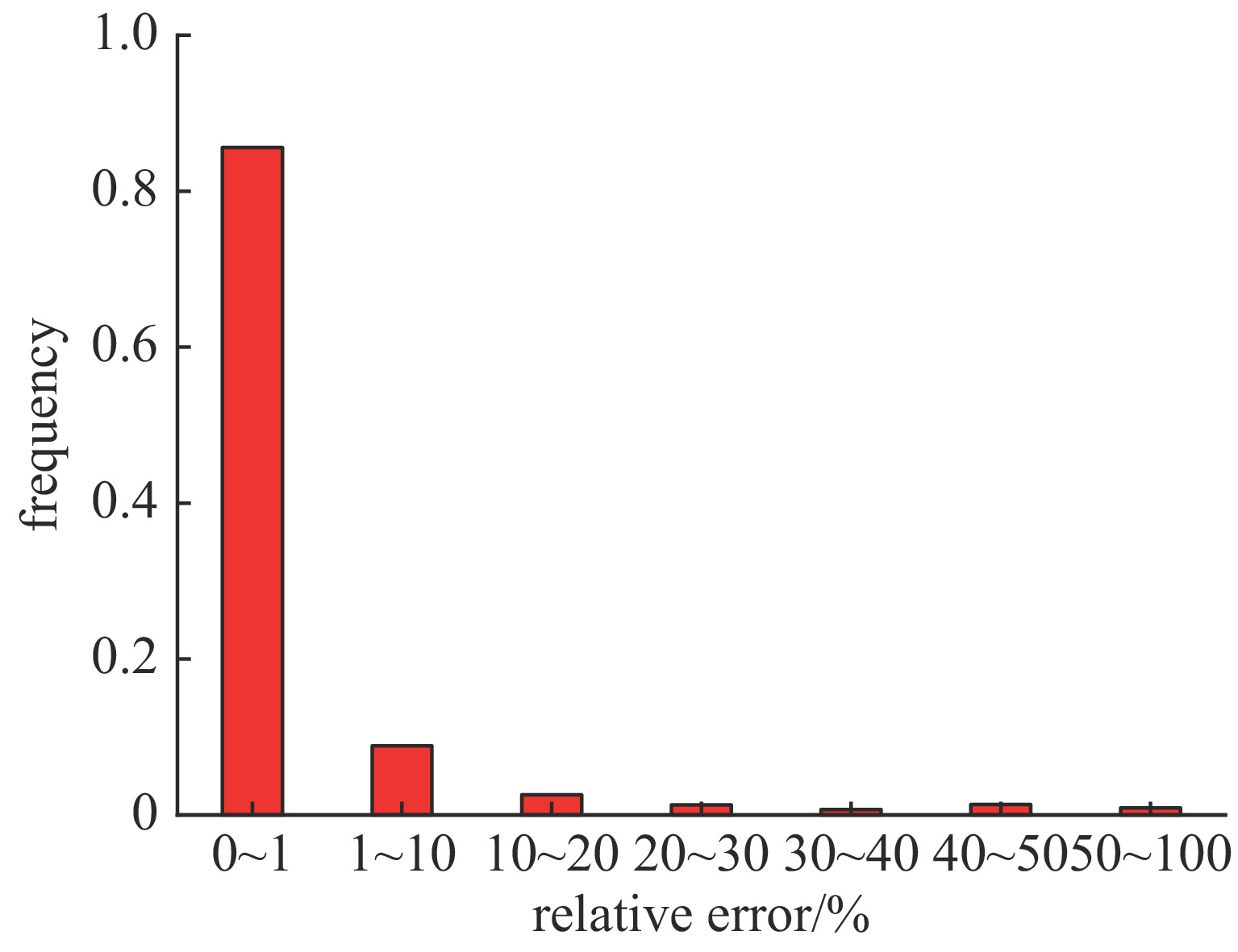
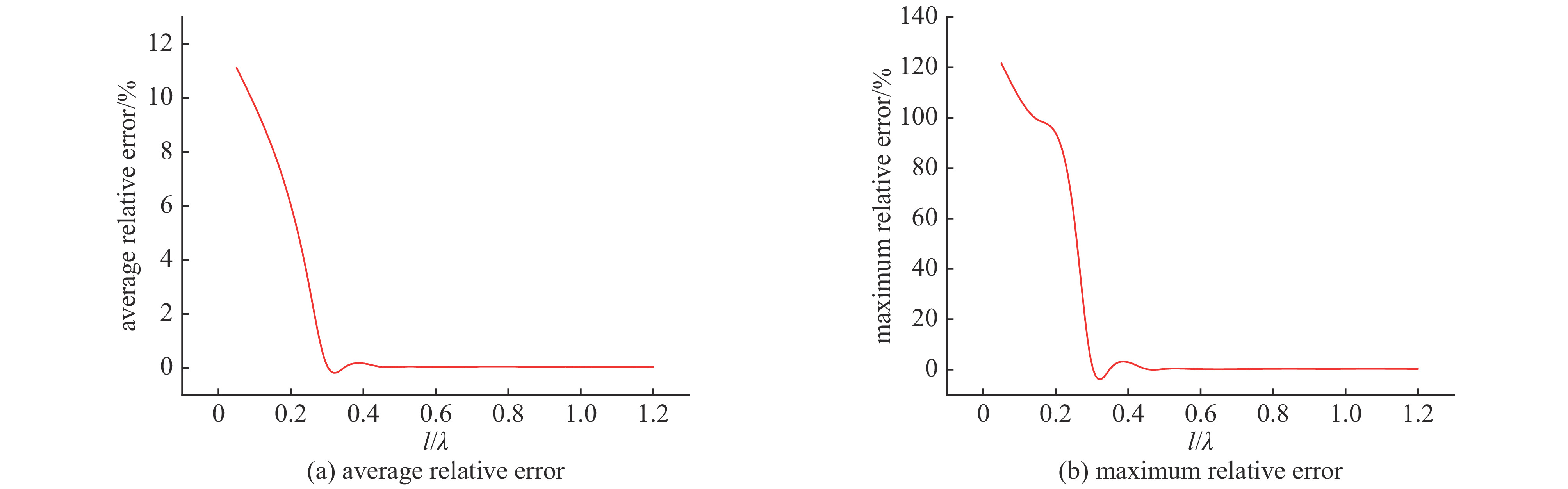
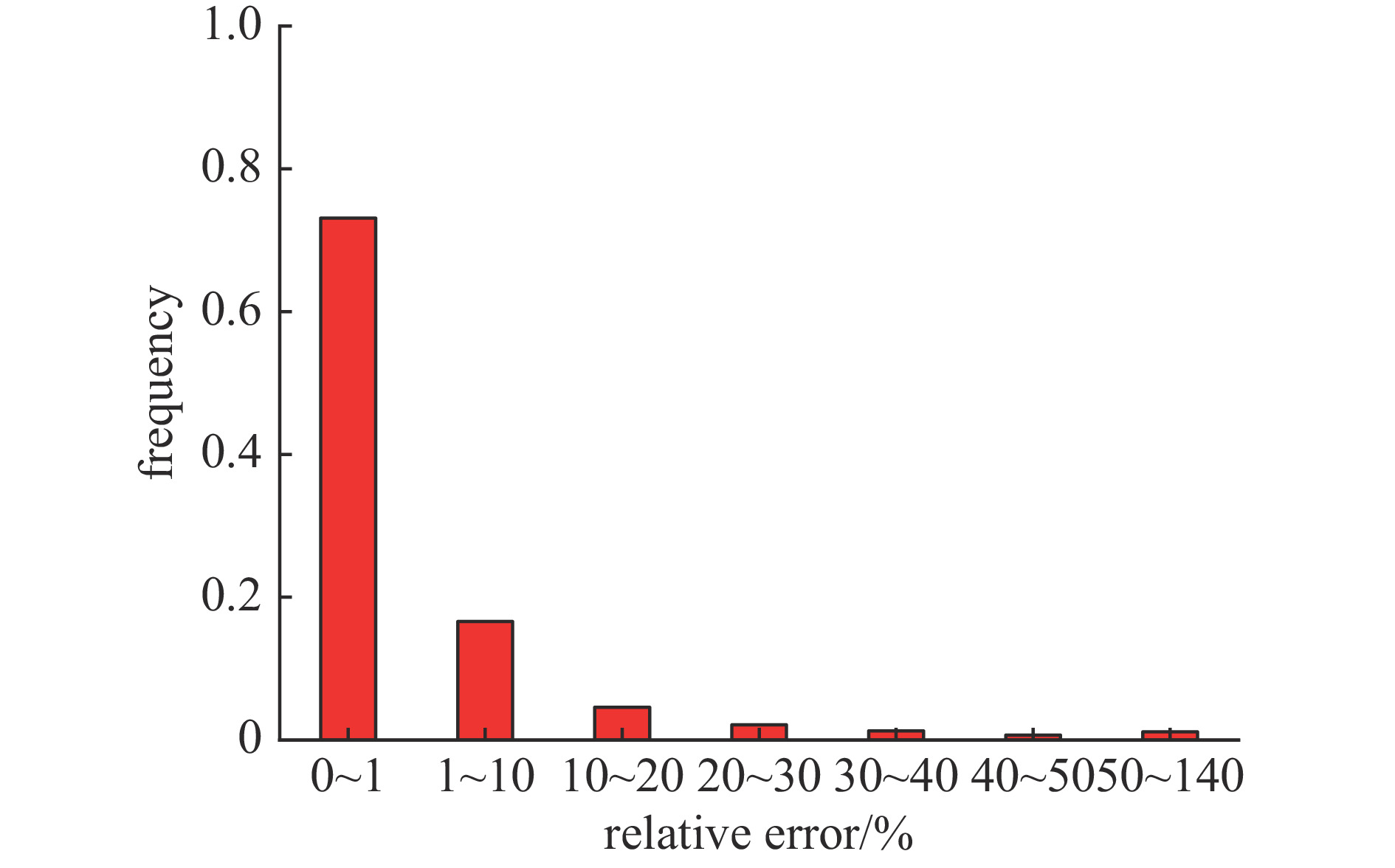
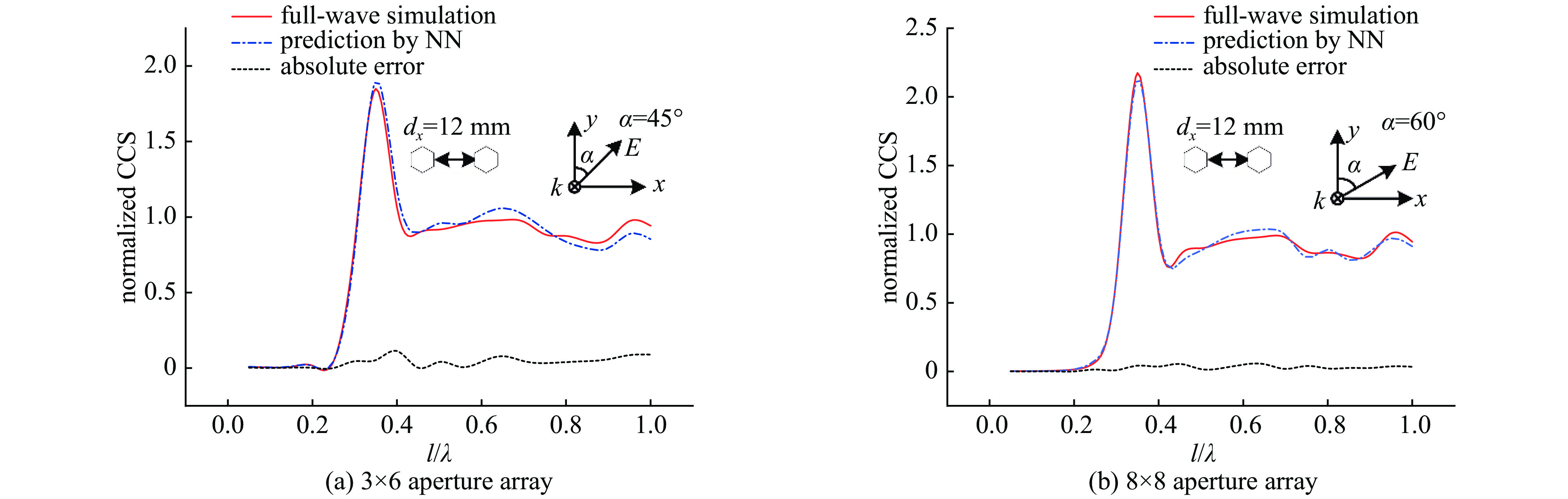
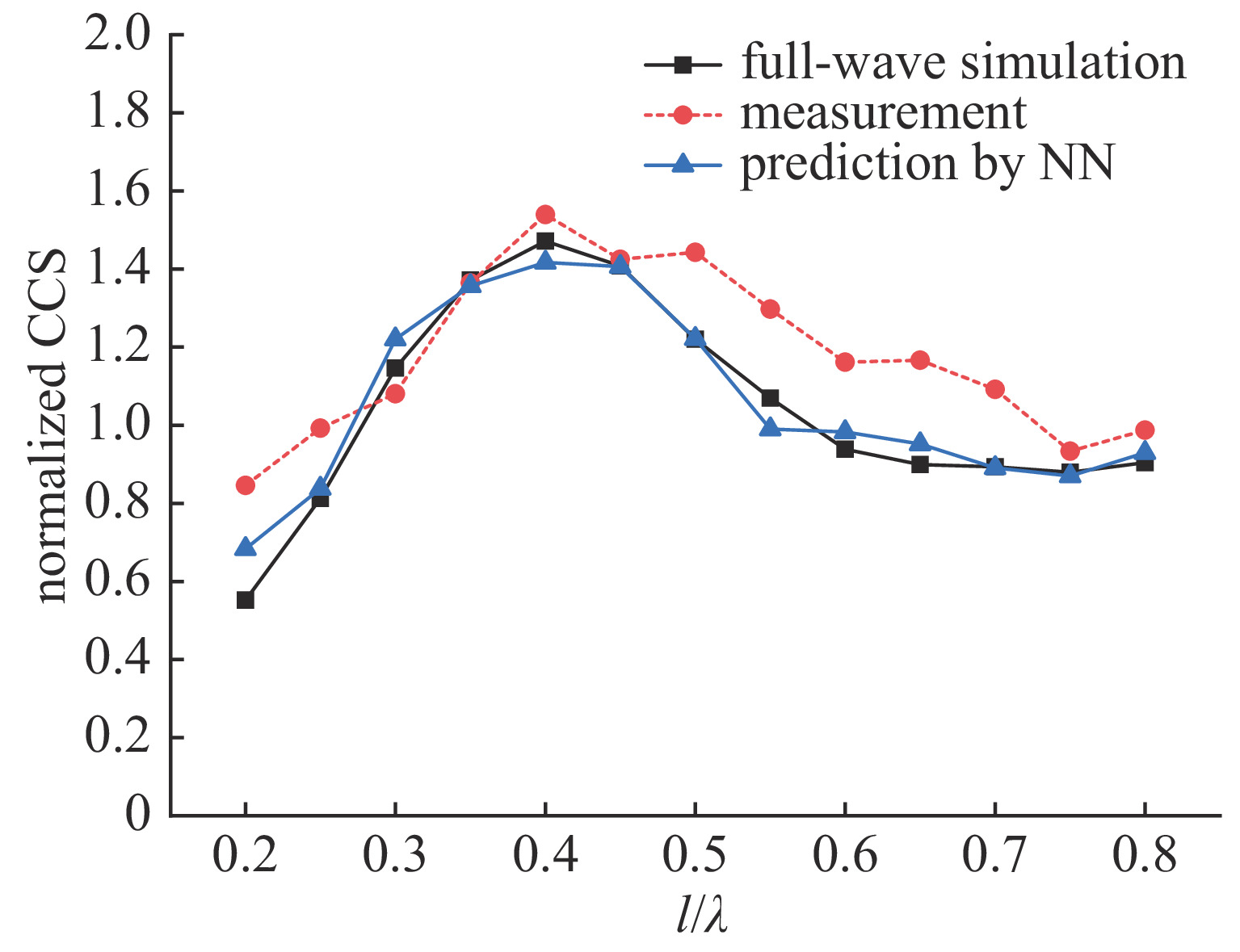
摘要: 孔缝耦合截面作为度量电磁能量经孔缝泄漏强弱的重要参数，一直没有一个普适快速且精度较高的获取方法。针对六边形孔阵归一化耦合截面的获取问题，分析了垂直入射条件下各因素对六边形孔阵耦合截面的影响，选择合适的参数并使用全波分析法共获取13820组耦合截面数据。对部分输入参数进行预处理后输入神经网络进行训练，构建了一个以孔单元电尺寸、行/列数、行/列间距电尺寸、孔壁厚度电尺寸、入射波极化角度等7个参数为输入，归一化耦合截面为输出的BP神经网络模型。该模型在预测电尺寸为[0.1，1.2]时的归一化耦合截面平均相对误差为3.8%。选取未出现在神经网络训练集与测试集中的输入参数，比较全波分析法计算值和神经网络预测值共480组数据，其平均相对误差为7.27%。最后通过实验测量，进一步验证了该模型的普适性和有效性。Abstract: As an important parameter to measure the leakage of electromagnetic energy through apertures, there has not been a universal, fast and high precision method to obtain the coupling cross section (CCS). For obtaining the hexagonal aperture array normalized CCS, we analyze the influence of various factors on it under the condition of vertical incidence. A total of 13820 sets of CCS data are obtained by selecting appropriate parameters and using full-wave analysis method. After some input parameters are preprocessed and the neural network is trained, a BP neural network model has been constructed with seven parameters including the electrical dimension of the aperture unit, row/column number, the electrical dimension of the row/column distance, the electrical dimension of the aperture wall thickness and polarization angle of incident wave as the input and the normalized CCS as the output. The model has an average relative error of 3.8% when the predicted normalized CCS of the hexagonal aperture array has the electrical dimensions [0.1, 1.2]. A total of 480 CCSs with input parameters not appearing in both the training set and the test set are predicted by the neural network and compared with the full-wave analysis results, and the average relative error is 7.27%. Finally, the universality and effectiveness of the model are validated further by experimental measurement.
-
图 4 其他极化角度与0°归一化耦合截面绝对差值
Figure 4. Absolute difference of normalized CCS between other polarization angles and 0°
图 5 电尺寸为0.295时孔阵归一化耦合截面随极化角度和孔间距电尺寸的变化
Figure 5. Variation of normalized CCS with α and
$ {d}_{x}/\lambda $ while l/λ is 0.295
图 6 神经网络拟合结果相对误差分布直方图
Figure 6. Histogram of relative error distribution of neural network fitting results
图 7 电尺寸与神经网络拟合结果误差关系图
Figure 7. Relation between
$ l/\lambda $ and error of neural network fitting result
图 8 神经网络预测结果相对误差分布直方图
Figure 8. Histogram of relative error distribution of neural network prediction results
图 9 神经网络预测值与真实值比较图
Figure 9. Comparison of predicted values of neural network and true values
图 11 实验测量结果与神经网络预测结果对比
Figure 11. Comparison of predicted values of neural network and experimental result
表 1 输入参数变化范围
Table 1. Range of input parameters
$ \mathit{l}/\mathit{\lambda } $ $ {\mathit{n}}_{\mathit{x}} $ $ {\mathit{n}}_{\mathit{y}} $ $ {\mathit{d}}_{\mathit{x}}/\mathit{\lambda } $ $ {\mathit{d}}_{\mathit{y}}/\mathit{\lambda } $ $ \mathit{\alpha } $ $ \mathit{h}/\mathit{\lambda } $ 0.05～1.20 1～8 1～8 0.025～3.000 0.025～3.000 0～$ \mathrm{\pi }/2 $ 0.0005～3.0000 
下载: 导出CSV
-
[1] Cho Y, Son H W, Choi J Y. Transmission resonance through small apertures[C]//2012 International Symposium on Antenna Technology and Applied Electromagnetics. 2012: 1-3. [2] Lee S W, Zarrillo G, Law C L. Simple formulas for transmission through periodic metal grids or plates[J]. IEEE Transactions on Antennas and Propagation, 1982, 30(5): 904-909. doi: 10.1109/TAP.1982.1142923 [3] Martin T, Backstrom M, Loren J. Semi-empirical modeling of apertures for shielding effectiveness simulations[J]. IEEE Transactions on Electromagnetic Compatibility, 2003, 45(2): 229-237. doi: 10.1109/TEMC.2003.810818 [4] Gunnarsson R, Bäckström M. Transmission cross section for apertures and arrays calculated using time-domain simulations[C]//International Symposium on Electromagnetic Compatibility. 2014: 169-174. [5] Hill D A, Ma M T, Ondrejka A R, et al. Aperture excitation of electrically large, lossy cavities[J]. IEEE Transactions on Electromagnetic Compatibility, 1994, 36(3): 169-178. doi: 10.1109/15.305461 [6] Holloway C L, Hill D A, Sandroni M, et al. Use of reverberation chambers to determine the shielding effectiveness of physically small, electrically large enclosures and cavities[J]. IEEE Transactions on Electromagnetic Compatibility, 2008, 50(4): 770-782. doi: 10.1109/TEMC.2008.2004580 [7] Levine H, Schwinger J. On the theory of electromagnetic wave diffraction by an aperture in an infinite plane conducting screen[J]. Communications on Pure and Applied Mathematics, 1950, 3(4): 355-391. doi: 10.1002/cpa.3160030403 [8] Huang C, Kodis R D. The measurement of aperture transmission coefficients[R]. Cruft Lab Harvard University, 1953: 165. [9] Huang Cha’ang, Kodis R D, Levine H. Diffraction by apertures[J]. Journal of Applied Physics, 1955, 26(2): 151-165. doi: 10.1063/1.1721953 [10] Koch G F, Kolbig K S. The transmission coefficient of elliptical and rectangular apertures for electromagnetic waves[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(1): 78-83. doi: 10.1109/TAP.1968.1139108 [11] Rahmat-Samii Y, Mittra R. Electromagnetic coupling through small apertures in a conducting screen[J]. IEEE Transactions on Antennas and Propagation, 1977, 25(2): 180-187. doi: 10.1109/TAP.1977.1141554 [12] Davis J G, Shakespeare P, Kiley N. Evaluation of circular aperture transmission coefficients in the presence of obscurations[C]//IET 8th International Conference on Computation in Electromagnetics (CEM 2011). 2011: 1-2. [13] 祝磊, 刘强, 赵翔, 等. 基于BP神经网络的圆形孔缝耦合截面预测[J]. 强激光与粒子束, 2019, 31:033201. (Zhu Lei, Liu Qiang, Zhao Xiang, et al. Prediction of coupling section of circular aperture based on BP neural network[J]. High Power Laser and Particle Beams, 2019, 31: 033201 doi: 10.11884/HPLPB201931.190011 [14] 丁星丽, 赵翔, 闫丽萍, 等. 基于神经网络的圆孔阵列垂直入射耦合截面预测[J]. 无线电工程, 2020, 50(5):383-389. (Ding Xingli, Zhao Xiang, Yan Liping, et al. Prediction of vertical incident coupling cross section of circular aperture array based on neural network[J]. Radio Engineering, 2020, 50(5): 383-389 doi: 10.3969/j.issn.1003-3106.2020.05.009 [15] Paoletti U, Suga T, Osaka H. Average transmission cross section of aperture arrays in electrically large complex enclosures[C]//2012 Asia-Pacific Symposium on Electromagnetic Compatibility. 2012: 677-680. [16] Olyslager F, Laermans E, De Zutter D, et al. Numerical and experimental study of the shielding effectiveness of a metallic enclosure[J]. IEEE Transactions on Electromagnetic Compatibility, 1999, 41(3): 202-213. doi: 10.1109/15.784155 [17] 李锐. 微波脉冲与带孔阵腔体、带介质窗口腔体耦合的研究[D]. 长沙: 国防科学技术大学, 2007Li Rui. Study on the coupling of microwave pulses into the cavity with aperture arrays and the cavity with a dielectric slot[D]. Changsha: National University of Defense Technology, 2007 -
点击查看大图
计量
- 文章访问数: 784
- HTML全文浏览量: 241
- PDF下载量: 29
- 被引次数: 0
