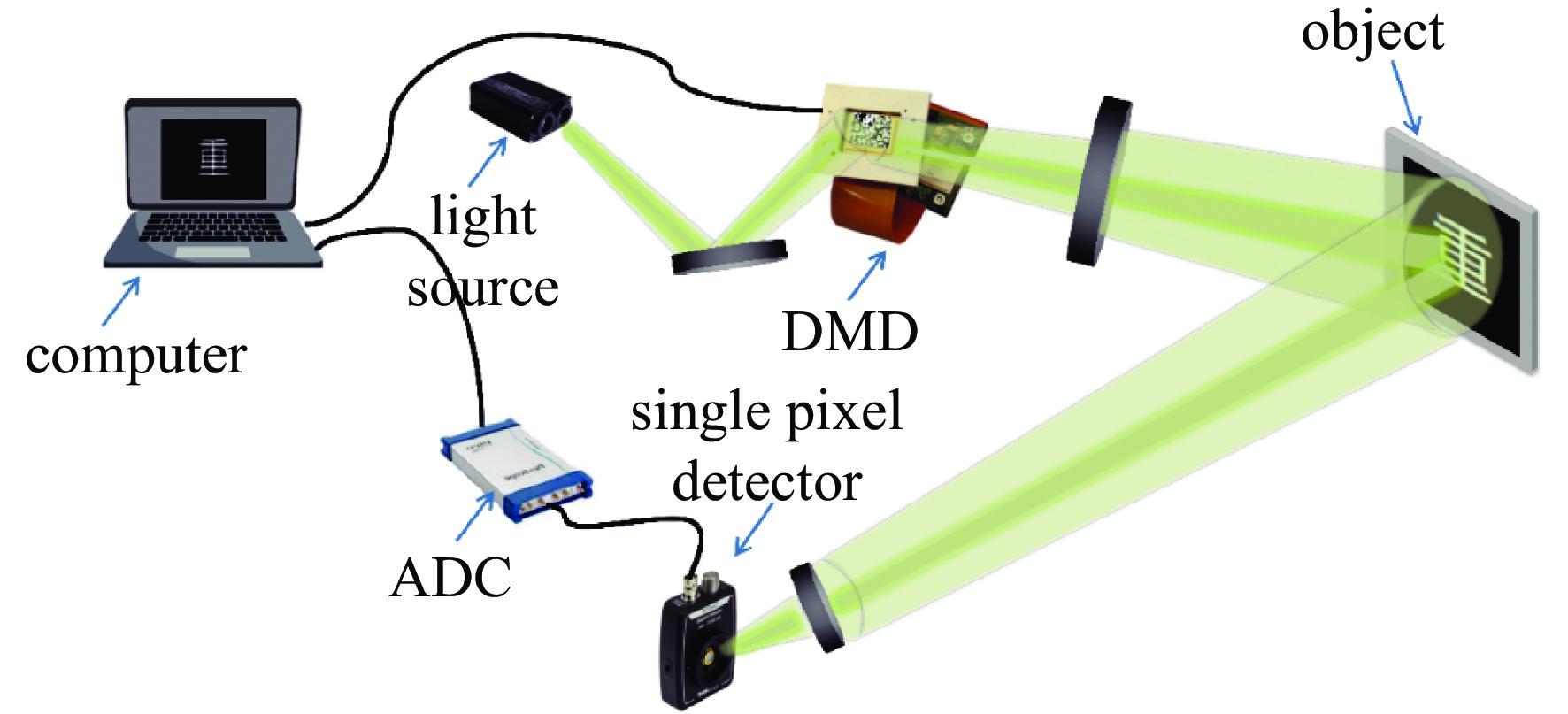
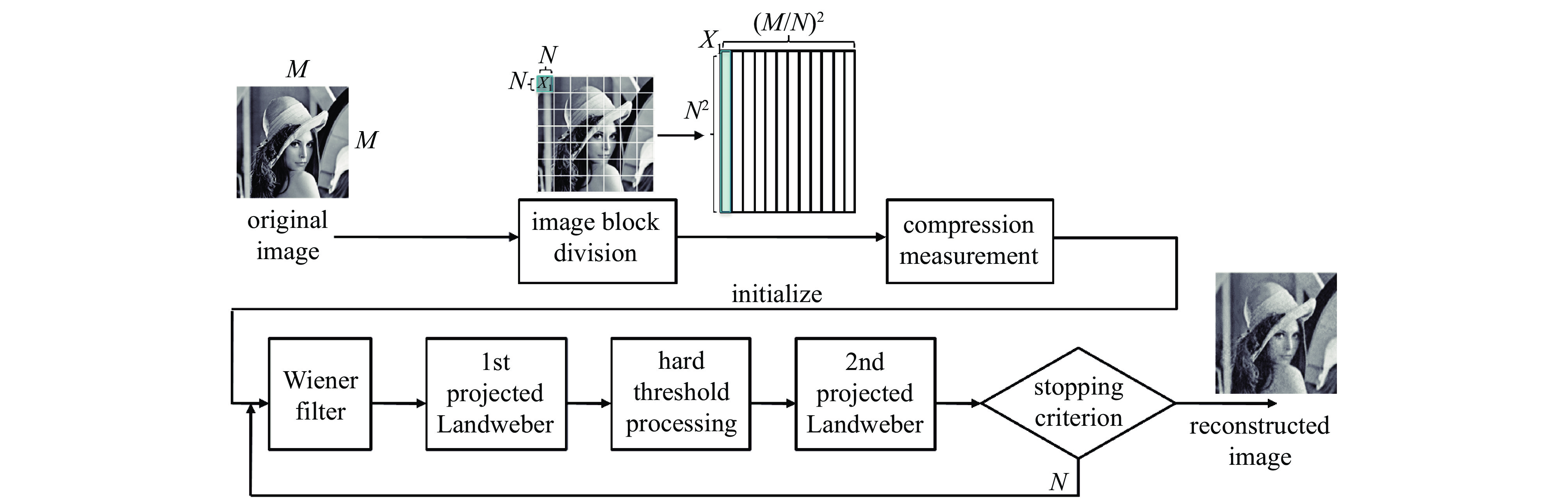
Single-pixel imaging system based on block smoothed projected quadratic reconstruction algorithm
-
摘要: 单像素成像系统是通过无空间分辨能力的单像元探测器来获取目标二维分布信息的计算光学成像技术,与传统直接成像技术相比具有高能量收集效率、高灵敏度等一系列优点,在高能物理诊断技术领域有着广阔的应用前景。针对实际单像素压缩感知成像系统在复杂诊断环境中存在的重建噪声较大的问题,提出并实现了基于分块平滑投影Landweber二次重构算法的单像素成像系统。根据算法观测矩阵分布特性以及数字微镜硬件输入要求实现了实际投影观测矩阵的变换,利用二次重构算法实现了单像素诊断的仿真分析与实验测试。仿真结果表明,在采样率为20%~30%的条件下,重建图像峰值信噪比大于20 dB,结构相似性高于0.8。进一步搭建单像素成像平台完成实验研究及验证,实验结果表明,利用二次重构算法模型对目标场景进行恢复的效果优于其余两种传统算法。二次重构单像素成像系统在采样率仅为20%的条件下能够重建出清晰的原始图像,具有较好的噪声抑制特性。
-
关键词:
- 单像素成像 /
- 光学成像系统 /
- 压缩感知 /
- 平滑投影Landweber算法 /
- 观测矩阵
Abstract: The single-pixel imaging system is a computational optical imaging technology that obtains the two-dimensional distribution information of the target through a single-pixel detector without spatial resolution. Compared with traditional direct imaging technology, it has a series of advantages such as high energy collection efficiency and high sensitivity. In the field of high-energy physical diagnosis technology it has broad application prospects. Aiming at the problem that the actual single-pixel compressed sensing imaging system has large reconstruction noise in complex diagnostic environments, this paper proposes and implements a single-pixel imaging system based on the block smooth projection Landweber quadratic reconstruction algorithm. According to the distribution characteristics of the algorithm's observation matrix and the digital micromirror hardware input requirements, the transformation of the actual projection observation matrix is realized, and the simulation analysis and experimental test of the single-pixel diagnosis are realized by using the quadratic reconstruction algorithm. The simulation results show that under the condition of a 20% to 30% sampling rate, the peak signal-to-noise ratio of the reconstructed image is greater than 20 dB, and the structural similarity is higher than 0.8. The single-pixel imaging platform is further built to complete the experimental research and verification. The experimental results show that the recovery effect of the target scene using the quadratic reconstruction algorithm model is better than the other two traditional algorithms. The quadratic reconstruction single-pixel imaging system can reconstruct a clear original image with a sampling rate of only 20%, and has good noise suppression characteristics. -
当宇宙空间中的高能粒子(主要是质子)克服地磁场的屏蔽作用进入到地球空间时,便会与大气中的氮、氧等原子发生核反应,产生大量的次级粒子,如中子、质子、电子、γ、π介子和μ子等,由此构成主要的大气辐射环境,其中中子是最主要的辐射粒子[1-2]。中子可通过与微电子器件的材料发生核反应产生的次级重离子在其敏感区域的电离来引发单粒子效应(SEE)。目前,大气中子被认为是临近空间(距地面20~100 km所包含的空域)、航空空间(距地面20 km以下空域)和地面附近的微电子器件发生单粒子效应的主因[3-6]。
国际航空界非常重视大气中子环境及其辐射效应的研究,并制定了相关的技术标准,例如IEC TS 62396-1[7]。近年来,由于军事需求的牵引和技术进步的推动,临近空间的战略价值也逐渐引起各国的重视。各国在加强对临近空间进行全面探测的同时,临近空间飞行器也因具有航空器、航天器所不具有的优势,在通信保障、情报收集、侦察监视、气象预报等方面极具发展潜力,从而成为各国的研究热点[8-9]。显然,大气中子导致的单粒子效应会对临近空间飞行器的可靠运行构成重要威胁。大气中子在地面附近产生的单粒子效应自1993年开始被观察到[6],而这将给通信、金融、大数据、互联网等领域带来不利的影响。美国Renesas技术公司在几个不同海拔的地点对广泛应用于手机的低功耗静态随机存取存储器(SRAM)进行了实时软错误率(RTSER)实验[10]。法国国家科学研究院在阿尔卑斯山建立的海拔SEE实验欧洲平台自2006年起开始运行[11]。可见,国际上对大气中子在地面附近诱发的单粒子效应越来越重视。随着半导体工艺的发展,微电子器件的特征尺寸不断缩小,工作电压不断减小,工作频率不断增加,从而其SEE敏感性也越来越高[12],大气中子诱发器件发生单粒子效应的潜在危害也越来越大。
中子SEE截面的能量依赖关系是中子SEE研究中最重要的内容,该关系可用于预估微电子器件在各种不同中子辐射环境中的单粒子效应错误率。这方面的实验研究一般利用单能、准单能中子源装置来开展。一般引发微电子器件产生单粒子效应的中子能量阈值为几MeV,只有能量在其之上的中子才可引发单粒子效应[10]。几MeV至20 MeV能区内的单能中子主要通过不同的轻离子诱发核反应如T(p, n),7Li(p, n),D(d, n),T(d, n)等来获得[13]。其中,14 MeV左右的中子可使用造价低廉的高压倍加器通过T(d, n)反应产生,其工作电压不高,仅为几百kV,但粒子束流大,可达mA量级。由于这个原因,14 MeV中子源在世界各地被广泛建立并有效应用于SEE实验中[10, 14-15]。中国原子能科学研究院(CIAE)的高压倍加器产生的14 MeV中子源也已多次应用于中子SEE实验研究中[16]。
在20 MeV以上能区,由于更高的入射能量会引发多体破裂过程,因而仅能获得准单能中子源。中子SEE饱和截面对于预估微电子器件在大气中子辐射环境中的错误率具有极其重要的意义,而中子SEE截面一般在20 MeV以上才会饱和。此外,JEDEC-JESD89标准推荐使用14,50,100,150 MeV的中子进行单粒子效应测试[17]。因此,建设准单能中子源并用于开展中子SEE研究是极为必要的。本文将对准单能中子源及准单能中子SEE实验所涉及的各个方面进行系统介绍。目前,我国还没有已建成的准单能中子源,中国原子能科学研究院正在100 MeV质子回旋加速器上进行准单能中子源的建设,本文将为其提供重要参考。
1. 准单能中子源
1.1 7Li(p, n)7Be核反应
在20 MeV以上能区,7Li(p, n)7Be反应提供了强度最高、单色性最好的中子源,其原因在于[13]:质子质量较小,在材料中的能损和岐离最小;剩余核7Be的第一激发态和基态仅相差0.43 MeV,产生的两组中子的能量差小于靶厚引起的中子能量分辨(1~2 MeV),并且7Be处于基态和第一激发态的中子产额较高,处于其他激发态的中子产额很小,这使得其单色性较好;该反应的反应能小(小于2 MeV),因而产生的中子的能量较高。另外,金属Li有较好的热学性质,材料容易获取并能做成自支撑靶。鉴于此,国际上各个实验室均采用7Li(p, n)7Be反应来建立准单能中子源装置(见表 1)。表 1中ΔE指的是靶厚,即一定能量的质子在确定厚度的7Li靶中的能量损失。
institution country energy/MeV beam current/μA ΔE/MeV distance/m flux/(cm-2·s-1) UC Davis USA 40~60 10 1 3 6×105 UCL Belgium 20~65 10 2 3.3 106 TRIUMF Canada 70~200 0.3 0.7 ~1 105 TSL Sweden 25~180 10 1 3 3×105 RCNP Japan 392 1.0 1 ~1 3×105 TIARA Japan 30~85 3 2 5.2 1.2×105 CYRIC Japan 50~8520~50 3(H+)10(H-) 1 1.0 1.0×106~107 7Li(p, n)7Be反应产生的单能峰中子是前倾的,故一般使用0°角产生的中子作为中子源。如图 1所示,7Li(p, n)反应在0°角产生中子的能谱包含了一个单能峰和一个尾部连续谱,前者是由二体反应7Li(p, n0, 1)产生,后者是由像7Li(p, n3He)α这样的三体反应产生的,其中单能峰中子约占全部中子的40%~50%。7Li(p, n0, 1)反应的0°角微分截面在质子能量较高时几乎为常数:Baba等人的实验表明,在43~87 MeV能区,该值基本上在33~35 mb/sr之间[19];Watson等人在文献[20]中指出,在60~400 MeV能区该值为(35.5±1.5) mb/sr。一般单能峰的峰值能量要比入射质子能量小几MeV,这是由质子在靶中的能损以及7Li(p, n0, 1)7Be反应的反应能为负值造成的。
 图 1 日本理化学研究所(RIKEN)使用飞行时间法测量得到的不同能量质子轰击10 mm厚7Li靶在0°散射角距离靶12 m处的中子能谱[21]Figure 1. Energy spectra of quasi-monoenergetic neutron sources generated from a 10 mm thick 7Li target bombarded by protons of different energies at RIKEN. They were measured on the neutron beam line at 12 m from the 7Li target by the TOF method[21]
图 1 日本理化学研究所(RIKEN)使用飞行时间法测量得到的不同能量质子轰击10 mm厚7Li靶在0°散射角距离靶12 m处的中子能谱[21]Figure 1. Energy spectra of quasi-monoenergetic neutron sources generated from a 10 mm thick 7Li target bombarded by protons of different energies at RIKEN. They were measured on the neutron beam line at 12 m from the 7Li target by the TOF method[21]1.2 准单能中子源装置布局
下面选择日本原子能机构高崎先进辐射研究所(TIARA)的准单能中子源装置[19]作为一种典型装置(见图 2)对其布局加以详细介绍。TIARA通过一台方位磁场可变回旋加速器(能量常数K=110)提供质子束轰击7Li靶(含99.8%的7Li)来产生中子。为兼顾产生的单能峰中子的能量分辨和产额,靶厚选择为质子穿过靶产生的能损为2 MeV时所对应的厚度,靶厚的选择与入射质子的能量有关。在可以远程控制的靶转换器上安装有7块7Li靶、1块氧化铝荧光屏(可观察质子束流)。当提供的质子束能量不同时,可方便地通过靶转换器选择厚度合适的7Li靶来产生相应的准单能中子。另外,考虑到质子在穿过7Li靶时会产生一定的热量(表 1质子流强为3 μA、靶厚为2 MeV的情况下产生的热功率为6 W),该靶转换器还能够进行水冷。由于7Li靶为薄靶,绝大多数质子将穿透7Li靶,这些质子由一个清扫磁铁偏离出中子束,进入一个屏蔽好的法拉第筒中,该法拉第筒可测量偏转过来的质子束流强度,同时起到束流收集器的作用。质子绝大部分能量损失在法拉第筒中,这会产生大量的热量,需对其冷却。旋转快门(由铁和聚乙烯构成)、铁过滤器、铁块以及外围的约3 m厚的混凝土墙可对0°角产生的中子束流进行准直和屏蔽,从而可在距7Li靶约为5.2 m的实验区获得准直较好的、本底较低的直径为11 cm或者更小的中子束斑用于SEE实验。真空系统在图 2所示的过滤器的末端结束,由一块2 mm厚的不锈钢板使之与大气隔绝。238U裂变电离室放置在7Li靶附近,232Th裂变电离室放置在偏转磁铁之后,二者均未放在中子束流中心位置,但二者的计数率均与产生的中子注量率成正比,此外法拉第筒测量的电流也与其成正比,故可利用这三个探测器作为束流监督器。该装置产生的中子注量率在104~105 (cm-2·s-1)量级,尽管强度比较低,但已有效应用到SEU研究中,用于观察SEU瞬变过程中的电流波形。国际上其他的准单能中子装置布局与TIARA大体都是相似的。
1.3 中子注量率
根据表 1中国际上用于SEE研究的各7Li(p, n)中子源装置的相关参数可知,这些准单能中子源装置的质子束流为1~10 μA,靶厚为1~2 MeV,靶与实验点之间的距离为1~5 m,实验点的中子注量率为105~107 (cm-2·s-1)。中子与质子均是通过核反应引起单粒子效应,且在50 MeV以上时可认为二者引起的SEE截面是相等的[17]。用于SEE实验的质子注量率一般为108 cm-2·s-1量级,因此中子注量率最好也能达到该量级。若考虑到准单能中子有50%~60%的尾部连续中子,而这部分中子能量比单能峰中子低,引起的SEE截面应该也比单能峰中子低,故用于SEE实验的准单能中子注量率应该比以相应入射质子进行质子SEE实验时的质子注量率高一些才好。准单能中子是由质子核反应产生,而核反应发生的几率很小,这就导致准单能中子源的强度受到一定限制。日本东北大学回旋加速器和同位素中心(CYRIC)的准单能中子源在表 1中各中子源中的中子注量率最高,达到了107 cm-2·s-1量级。该装置对经过加固的DRAM器件进行SEE测试一般需几小时的实验时间[22],时间仍然偏长。显然,注量率不足是国际上各准单能中子源都存在的问题。
中子注量率是准单能中子源装置设计中的关键问题,它与使用的质子流强I、7Li靶厚d、靶与实验点之间的距离L、冷却装置设计以及中子的准直和屏蔽设计等问题紧密相关。显然,实验点中子注量率
(1) 式中:NV为单位体积靶核数,e为元电荷电量,(0°)为0°角中子产生的微分截面。一般中子源的注量率均难以达到108 cm-2·s-1量级,能够做到的只是通过合理设计在一定范围内使中子注量率增大。由式(1)可见,增大质子流强、使用厚靶、减小靶与实验点之间的距离是提高中子注量率的三种方法。其中增大质子流强比较简单,但是大部分加速器的质子流强也有一定限值,一般小于10 μA,另外这种方法在一定程度上会加大加速器设备的辐射损伤和活化。而7Li靶不宜太厚,否则会破坏中子的单能性,一般取靶厚为1~2 MeV。对中子进行准直和屏蔽,使得靶与实验点之间一般有数m的距离,而注量率与距离的平方成反比,故使该距离减小对于增大注量率极为有效。比如,瑞典Svedberg实验室(TSL)最初的中子源,其靶与实验点之间距离长达11 m,导致SEE实验能够获得的中子注量率十分有限,后经改造将此距离缩减至3 m,从而将注量率提高了1个量级以上。CYRIC为获得高的中子注量率,通过模块化的屏蔽结构设计,使靶与实验点之间的距离近至1 m。加拿大TRIUMF实验室和日本大阪大学核物理研究中心(RCNP)也采用较短的靶与实验点之间距离(1 m)以补偿其质子流强的不足。此外,CYRIC对50 MeV以下的质子采用负离子束流,这样质子流强可由3 μA提高到10 μA,从而增大中子注量率。
1.4 中子能谱的理论计算与实验测量
质子与7Li核反应属于轻核反应,其相应的核能级间隔较大,故基于预平衡反应理论和平衡衰变理论的较成熟的核反应模型对其不适用,这给核反应的计算带来了一定难度[23]。图 3为核反应计算程序TALYS[24]以及处理粒子与物质相互作用的蒙特卡罗程序Geant4[25],Fluka[26]计算的100 MeV质子与7Li核反应产生的准单能中子能谱。可见,TALYS计算的能谱中有两个相隔较远的单能峰,且峰的位置偏低;Geant4计算的能谱中没有单能峰的存在;Fluka计算的能谱中单能峰中子占比过少。将100 MeV质子与7Li核反应产生中子的0°角微分截面的单能峰中子部分按35.5 mb/sr计算,单能峰中子占产生的全部中子的比例按40%计算[27],则产生中子的0°角微分截面为88.75 mb/sr。TALYS,Geant4计算的0°角微分截面均约为21 mb/sr,过小;Fluka计算的结果约为88 mb/sr,基本合理。此外,蒙特卡罗程序PHITS通过结合核内级联模型和考虑分立核能级的扭曲波波恩近似能够给出正确的单能峰部分的中子能谱,但尾部中子的谱形仍偏离于正确的形状[28]。这些程序在计算该反应时给出错误结果的原因应该在于其采用的核反应模型不适用。
在7Li(p, n)反应的理论计算方面,一般是对产生单能峰中子的二体反应和产生尾部连续中子的三体反应分别进行研究的。对于二体反应7Li(p, n0, 1),Taddeuchi等人指出,其微分截面dσ/dΩ可视为动量转移的函数,并给出了计算其值的参数化模型[29]。另外,Uwamino等人给出了由7Li(p, n0, 1)截面确定0°角微分截面的经验公式[30]。对于7Li(p, n3He)α等三体反应,Ohlsen发现,产生的中子的能谱可用三体相空间方法来进行计算[31]。一般而言,仅考虑7Li(p, n3He)α反应就可以计算出较好的尾部连续中子谱。由于该方法计算出的尾部较高能部分中子在相空间分布有所偏离,Prokofiev等人对50~200 MeV质子能区提供了一个半经验公式来对其进行修正[27]。Mashnik等人[23]依据现有的7Li(p, n0, 1)反应截面的实验数据对150 MeV以下质子能区的7Li(p, n)反应进行了核数据评价,质心系的7Li(p, n0, 1)反应微分截面可采用勒让得多项式进行拟合得到,尾部连续中子采用GNASH核反应程序[32]计算得到。经蒙特卡罗程序MCNP6检验,该方法得出的核数据与实验吻合得较好[33]。
在准单能中子能谱的实验测量方面,主要有三种方法:反冲质子法、飞行时间法和多球中子谱仪法。
反冲质子法多采用聚乙烯为辐射体,以ΔE-E探测器对反冲质子进行探测。该方法的优点是能量分辨率较高、信噪比较高,缺点是探测效率太低。为提高探测效率,Baba等人在TIARA准单能中子源上使用长的铜棒将束流中心处的中子屏蔽掉,而边缘处的中子进入环形聚乙烯辐射体后产生的反冲质子用ΔE-E探测器进行探测[19]。由于质子在探测器元件和空气中的能损,该方法只能测量到低至约12 MeV的中子能谱。在这种情况下,可用三体相空间方法将能谱外推至更低能段。
飞行时间法多使用液体闪烁体(BC501或NE213)和238U裂变电离室为探测器。使用液体闪烁体作探测器时,与反冲质子法一样,由于20 MeV以上能区的n-p散射微分截面缺乏实验数据,相应的数据处理中会引入较大误差[34]。由蒙特卡罗程序SCIFUL和CECIL计算的液体闪烁体探测器响应函数与实验值相差较大[35-36],因此Baba等人使用在反冲质子法中得到的中子能谱对其响应函数进行标定,并依此对程序中的相关参数进行修正,进而应用到飞行时间法中[19]。飞行时间法测量中子能谱的能量下限与脉冲重复周期、探测器响应阈值、数据获取系统的量程及其对粒子的甄别能力等均有关系。为实现对低能量中子的探测,一般要采取束流调制器来增大脉冲重复周期(1 μs),以避免相邻两脉冲中前一脉冲的低能中子信号与后一脉冲的高能中子信号的叠加效应。Nakao等人使用NE213液体闪烁体作为探测器,通过改进数据获取系统来增大其量程并有效去除光子及逃逸质子造成的干扰,从而获得了低至7 MeV左右的准单能中子能谱[37]。238U裂变电离室对光子及1.4 MeV以下的中子几乎完全不响应,Schuhmacher等人以其作为探测器获得了低至2 MeV左右的准单能中子能谱[34]。飞行时间法测量结果的精确度较高,与反冲质子法获得的结果,在误差范围内一致。
多球中子谱仪采用不同尺寸的聚乙烯球作慢化体。为了提高对能量大于20 MeV中子的探测效率,需嵌入Cu, Pb, W等辅助材料层,并将3He气体探测器置于其中心作探测器,通过使用不同慢化体时探测器计数率的不同对中子能谱进行反推。该方法的优点是能谱测量范围宽,从热中子到单能峰中子都可以探测,从而可测量到前两种方法不能测量的低能区域的中子,补充前两种方法的不足。缺点是能量分辨率差,且解谱过程对最终得到的中子能谱的影响较大。Bedogni等人使用多球中子谱仪对TSL的50~180 MeV质子产生的准单能中子进行了实验测量[38]。
1.5 中子束流轮廓及其均匀性
SEE实验一般对入射粒子的束斑大小及其均匀性有一定的要求,故应当对准单能中子束流轮廓进行实验测量。显然,这与7Li(p, n)反应产生的中子的角分布、准直器的内径以及测量位置与准直器出口之间的距离密切相关。在实验上,由于中子难以直接测量,通常应用转换体配合影像板对其进行测量。常用的转换体有高密度聚乙烯、铝箔等。快中子与高密度聚乙烯发生核反应的产物(主要是散射的质子)进入到影像板中,使其荧光层发光,影像板的光激励发光(PSL)值即反映了入射中子的强度[39]。快中子与铝箔发生核反应产生的轻带电粒子可进入到影像板中,使其荧光层发光,此外反应27Al(n, α)的产物24Na具有的β和γ放射性也可使其发光[40]。Shikaze等人利用高密度聚乙烯转换体和富士膜影像板(BAS-SR)对TIARA准单能中子源距准直器出口0.68,2,8 m位置处的中子束流轮廓进行了实验测量,由此确定相应的束斑大小[39]。Baba等人用铝箔转换体配合影像板对CYRIC准单能中子源在距7Li靶1 m的位置的中子束流轮廓进行了实验测量,结果(图 4)表明,中子束斑为直径约5 cm的圆形束斑,束斑的不均匀性为10%[22]。除了这种方法外,Schuhmacher等人应用铝箔转换体配合多丝正比室(MWPC)的方法对比利时鲁汶大学(UCL)准单能中子的束流轮廓进行了实验测量[34],多丝正比室面积较大,且对入射带电粒子具有位置分辨能力,在效果上相当于影像板。此外,Pomp等人利用薄膜击穿计数器(TFBC)对TSL的准单能中子源的中子束流轮廓进行了实验测量[41]。
1.6 热中子本底
微电子器件中一般会有一些含B材料,比如硼磷硅玻璃(BPSG)用于器件平整化。如果测试器件中存在大量B,热中子可通过10B(n, a)反应引起单粒子效应[42]。因此,产生的热中子需要被屏蔽,这通常采用Cd片或者B片来进行[43]。热中子的注量率通常采用金箔活化法来测量。Baba等人采用金箔活化法测量得到CYRIC准单能中子源的热中子本底在1×104 cm-2·s-1左右,在快中子注量率的1%以下[22]。
2. 准单能中子单粒子效应实验
进行准单能中子SEE实验时,需获取辐照微电子器件的中子注量Φ、辐照期间器件产生的SEE数目NSEE两个量。要得到中子注量Φ,需提前对辐照器件位置的中子能谱(cm-2·s-1·MeV-1)进行实验测量,由中子能谱对能量积分可得到中子注量率(cm-2·s-1),并对中子注量率与中子束流监督器的计数率之间的比例K进行实验标定。若辐照器件期间,中子束流监督器的累积计数为Nmon,则Φ=K×Nmon。准单能中子SEE实验的目的在于获取单能峰峰值能量对应的SEE截面,从而获得SEE截面的能量依赖关系。然而中子注量Φ中既包含了单能峰中子又包含了尾部连续中子,且尾部连续中子也可导致SEE,故峰值能量对应的SEE截面σ应该在NSEE/Φ与NSEE/Φpeak之间,其中:Φpeak为单能峰中子的注量;NSEE为实验期间测得的器件单粒子效应数目[44]。为获得较为准确的峰值能量对应的SEE截面,要对其尾部进行修正。
目前,主要有三种准单能中子SEE截面的尾部修正方法:迭代逆卷积方法、蒙特卡罗模拟方法和非零度中子实验扣除方法。一般认为SEE截面曲线σ(E)是平滑的,在迭代逆卷积方法[45-47]中假定曲线的形式可表达为线性的、双参数Bendel函数或Weibull函数。σ(E)满足方程
(2) 式中: 为实验期间辐照到器件上的中子的能谱(cm-2·MeV-1);Eth为σ(E)的阈值,一般需要开展刚超过阈值的低能单能中子SEE实验对Eth进行确定。峰值能量记为Epeak,先取σ(Epeak)=NSEE/Φ,其他能量处的截面根据所取的曲线形式进行确定,然后将此时的截面曲线代入式(2)右端进行积分,结果记为N′SEE。取σ(Epeak)为其上次取值的NSEE/N′SEE倍,同时调整其他能量处的截面,再代入式(2)右端进行积分,根据积分结果再对σ(Epeak)进行调整。不断重复此迭代过程,直到最后积分结果与NSEE极其接近为止,最后一次的σ(Epeak)即是修正后的峰值能量对应的SEE截面。
在蒙特卡罗模拟方法中,可根据微电子器件进行重离子、质子SEE的实验结果,利用处理粒子与物质相互作用的蒙特卡罗程序(常用的如Geant4,Fluka等)建立起该器件的RPP几何仿真模型[48],确定相应的敏感体积和临界电荷等关键参数,然后利用程序抽样出全能谱中子、单能峰中子,依次辐照器件的仿真模型,利用RPP模型的原理确定出这两种情况下的SEE数目Nall, Npeak,得到系数Cpeak=Npeak/Nall,则峰值能量中子导致的SEE截面为σ(Epeak)=CpeakNSEE/Φpeak。Lambert等人在TSL进行的准单能中子SEE实验即使用了这种方法进行尾部修正[46]。
南非国家加速器中心(NAC)对7Li(p, n)反应产生的中子进行的实验测量表明,当入射质子能量为100 MeV时,其输送到16°方向的中子几乎没有单能峰,谱形与0°方向连续本底中子情形十分接近[49],如图 5所示,其中N为监视器读数。因此,可同时在0°和16°方向进行SEE实验,通过用0°方向的SEE截面数据减去16°方向数据的方法来对尾部连续中子的影响予以扣除[10],即非零度中子实验扣除法。目前,NAC尚未将该方法应用于SEE研究,而CYRIC正在计划新增一个角度为20°左右的束流通道,使该方法的应用成为可能[10]。
3. 总结与讨论
大气中子是临近空间、航空空间和地面附近的微电子器件发生单粒子效应的最主要因素,对航空器、临近空间飞行器的可靠运行构成重要威胁,并给通信、金融、大数据、互联网等领域带来不利的影响。建设准单能中子源并用其开展SEE实验,对中子SEE截面的能量依赖关系进行研究,对于评估器件在大气中的抗中子辐照能力具有重要意义。本文对国际上用于SEE研究的准单能中子源进行了相关调研,对产生准单能中子的7Li(p, n)7Be核反应、装置布局以及中子注量率、中子能谱、中子束流轮廓及其均匀性、热中子本底等表征中子场性质的参数的理论计算及实验测量进行了系统介绍。在准单能中子场相关参数的实验测量方面:中子能谱可用反冲质子法、飞行时间法、多球中子谱仪法进行实验测量,其中前两种方法准确性较高,第三种可在低能区对前两者测得的中子能谱进行补充;中子束流轮廓及均匀性可采用转换体配合影像板进行测量;热中子本底可采用金箔活化法进行测量。中子注量率不能通过实验直接测量,只能由实验测量到的中子能谱积分得到,其准确性依赖于中子能谱的准确性。进行准单能中子SEE实验要求中子源应有较高的中子注量率水平,这样可缩短实验时间并减少实验数据的统计误差。同时,要求中子源能提供较大的束流轮廓、较好的束流均匀性以及较低的热中子本底,这样可提高实验数据的可靠性。此外,本文对如何进行准单能中子SEE实验以及SEE截面的尾部修正方法进行了简单介绍。从三种尾部修正方法的原理中可看出,在这三种方法中实验测量的中子能谱的准确性都是极其重要的,它在很大程度上决定了截面修正结果的准确性。
中国原子能研究院的100 MeV质子回旋加速器可提供70~100 MeV的质子,在准单能中子束线端可提供流强为20 μA的质子束流。为保证中子场良好的准单能性,屏蔽和准直系统设计得较为庞大,使得靶到实验点之间的距离约为5 m。经简单估算,在使用2 MeV能损的7Li靶情况下,100 MeV质子在实验点产生的全能谱中子注量率可达到1.26×106 cm-2·s-1。该准单能中子源装置的建设及中子场相关参数的实验测量预计将在2021年完成。将来可考虑在此准单能中子源装置上建设一条束流孔道将p与7Li核反应产生的16°角中子引出用于准单能中子SEE截面的尾部修正。该装置建成后除了用于单粒子效应研究外,也可进行核数据测量、辐射防护、中子治癌等方面的研究,还可以作为标准中子参考辐射场对中子探测器进行标定。
-
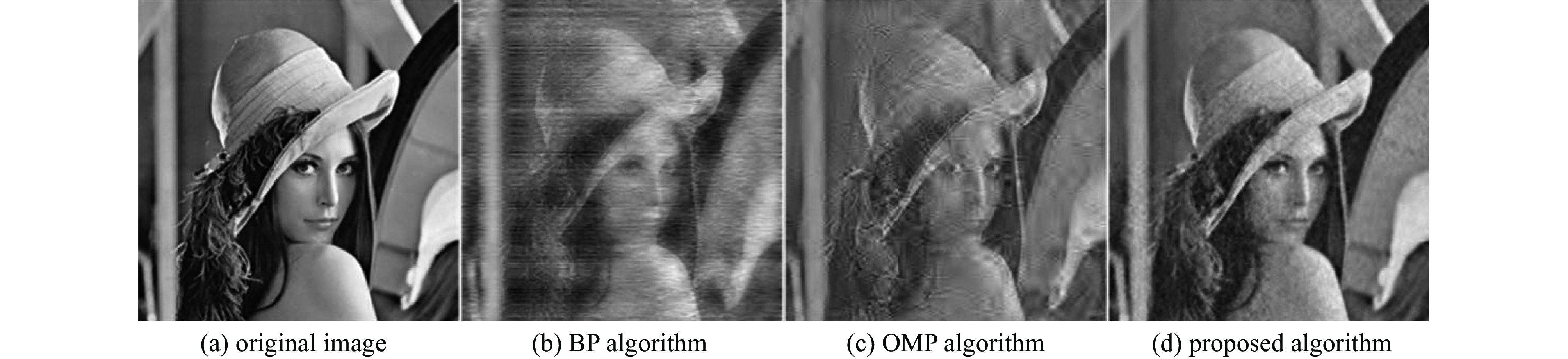
表 1 采样率30%时,不同重构算法间性能的比较
Table 1. Performance comparison between different reconstruction algorithms at 30% sampling rate
algorithm SSIM PSNR/dB reconstruction time/s BP 0.44 19.19 79.5 OMP 0.53 22.26 1.4 proposed algorithm 0.76 27.61 4.6 表 2 不同采样率下重建图像的PSNR和SSIM
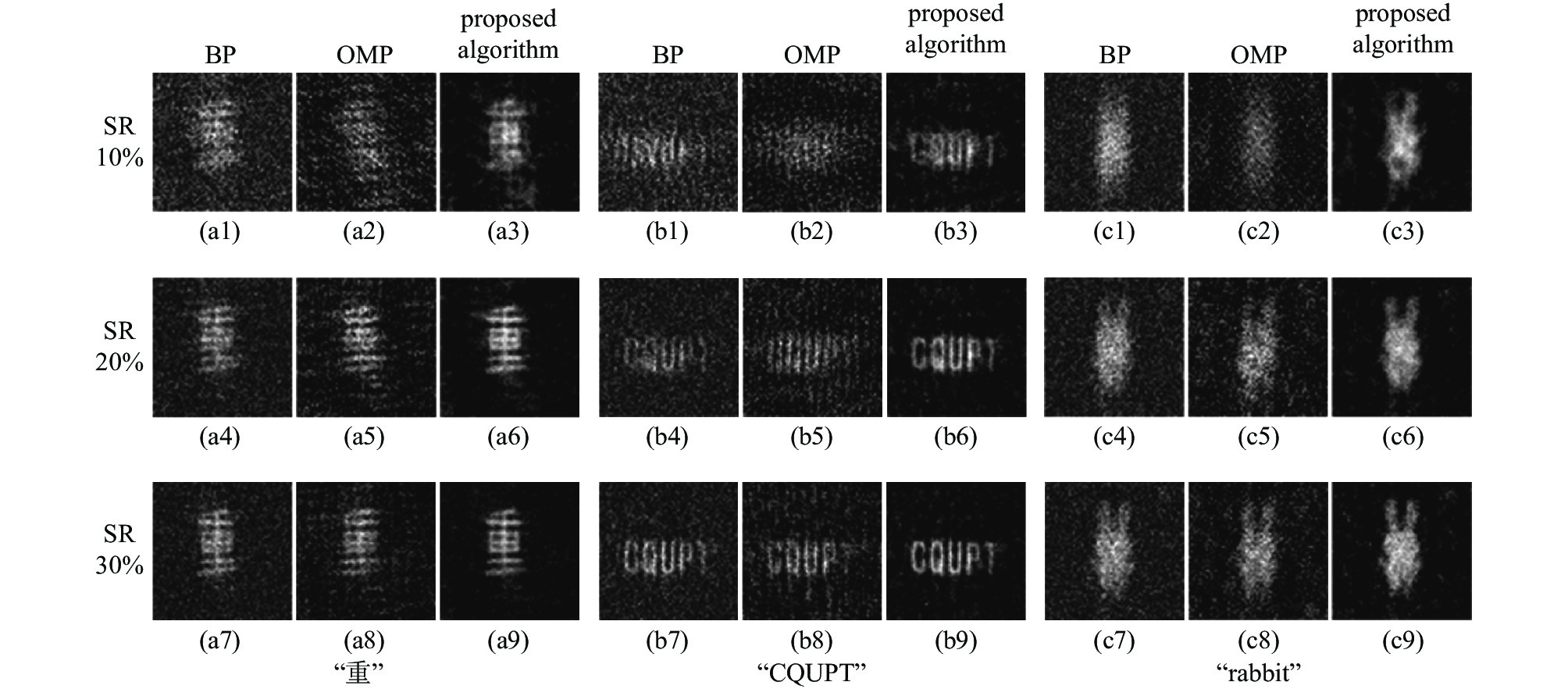
Table 2. PSNR and SSIM of reconstructed images at different sampling rates
image PSNR at different sampling rate/dB SSIM at different sampling rate 10% 20% 30% 10% 20% 30% “重” 19.46 21.60 23.66 0.61 0.83 0.86 “CQUPT” 16.90 20.44 23.19 0.56 0.80 0.82 rabbit 18.56 21.48 22.70 0.58 0.81 0.83 表 3 不同算法和采样率下图像重构所需时间
Table 3. Time required for image reconstruction under different algorithms and sampling rates
image algorithm time at different sampling rate/s 10% 20% 30% “重” BP 161.5 566.7 1026.1 OMP 0.9 1.8 2.9 proposed algorithm 2.6 3.6 4.7 “CQUPT” BP 155.5 566.6 1026.1 OMP 0.9 1.8 2.9 proposed algorithm 2.5 3.6 4.8 rabbit BP 155.8 589.1 1204.3 OMP 0.9 1.9 2.8 proposed algorithm 2.6 3.8 4.7 -
[1] 王峰, 关赞洋, 理玉龙, 等. 基于神光Ⅲ装置的光学诊断系统介绍[J]. 中国科学:物理学、力学、天文学, 2018, 48(6):48-58Wang Feng, Guan Zanyang, Li Yulong, et al. Optical diagnostic systems based on Shenguang Ⅲ[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2018, 48(6): 48-58 [2] Donoho D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. doi: 10.1109/TIT.2006.871582 [3] Candes E J, Romberg J, Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory, 2006, 52(2): 489-509. doi: 10.1109/TIT.2005.862083 [4] Candes E J, Tao T. Near-optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, 2006, 52(12): 5406-5425. doi: 10.1109/TIT.2006.885507 [5] Guan Zanyang, Li Yulong, Wang Feng, et al. Study on the length of diagnostic time window of CUP-VISAR[J]. Measurement Science and Technology, 2021, 32: 125208. doi: 10.1088/1361-6501/ac29d4 [6] 王峰, 理玉龙, 关赞洋, 等. 压缩感知技术在激光惯性约束聚变研究中的应用[J]. 强激光与粒子束, 2022, 34:031021 doi: 10.11884/HPLPB202234.210250Wang Feng, Li Yulong, Guan Zanyang, et al. Application of compressed sensing technology in laser inertial confinement fusion[J]. High Power Laser and Particle Beams, 2022, 34: 031021 doi: 10.11884/HPLPB202234.210250 [7] Duarte M F, Davenport M A, Takhar D, et al. Single-pixel imaging via compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 83-91. doi: 10.1109/MSP.2007.914730 [8] 李明飞, 阎璐, 杨然, 等. 基于Hadamard矩阵优化排序的快速单像素成像[J]. 物理学报, 2019, 68:064202 doi: 10.7498/aps.68.20181886Li Mingfei, Yan Lu, Yang Ran, et al. Fast single-pixel imaging based on optimized reordering Hadamard basis[J]. Acta Physica Sinica, 2019, 68: 064202 doi: 10.7498/aps.68.20181886 [9] 马彦鹏, 王亚南, 王义坤, 等. 基于压缩感知的单点探测计算成像技术研究[J]. 光学学报, 2013, 33:1211007 doi: 10.3788/AOS201333.1211007Ma Yanpeng, Wang Yanan, Wang Yikun, et al. Study of single-pixel detection computational imaging technology based on compressive sensing[J]. Acta Optica Sinica, 2013, 33: 1211007 doi: 10.3788/AOS201333.1211007 [10] 陈涛, 李正炜, 王建立, 等. 应用压缩传感理论的单像素相机成像系统[J]. 光学 精密工程, 2012, 20(11):2523-2530 doi: 10.3788/OPE.20122011.2523Chen Tao, Li Zhengwei, Wang Jianli, et al. Imaging system of single pixel camera based on compressed sensing[J]. Optics and Precision Engineering, 2012, 20(11): 2523-2530 doi: 10.3788/OPE.20122011.2523 [11] Wu Shaohua, Zhang Tiantian, Wu Bo, et al. Single-pixel camera in the visible band with fiber signal collection[J]. IEEE Access, 2018, 6: 17768-17775. doi: 10.1109/ACCESS.2018.2819358 [12] Wei Ziran, Zhang Jianlin, Xu Zhiyong, et al. Optimization methods of compressively sensed image reconstruction based on single-pixel imaging[J]. Applied Sciences, 2020, 10: 3288. doi: 10.3390/app10093288 [13] Mun S, Fowler J E. Block compressed sensing of images using directional transforms[C]//2009 16th IEEE International Conference on Image Processing (ICIP). Cairo: IEEE, 2009: 3021-3024. [14] Candès E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9/10): 589-592. [15] Chen S S, Donoho D L, Saunders M A. Atomic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing, 1998, 20(1): 33-61. doi: 10.1137/S1064827596304010 [16] Figueiredo M A T, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597. doi: 10.1109/JSTSP.2007.910281 [17] Mallat S G, Zhang Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. doi: 10.1109/78.258082 [18] Tropp J A, Gilbert A C. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12): 4655-4666. doi: 10.1109/TIT.2007.909108 [19] Needell D, Tropp J A. CoSaMP: iterative signal recovery from incomplete and inaccurate samples[J]. Communications of the ACM, 2010, 53(12): 93-100. doi: 10.1145/1859204.1859229 [20] 苏杰, 翟爱平, 赵文静, 等. 自适应斜Z字形采样Hadamard单像素成像[J]. 光子学报, 2021, 50:0311003 doi: 10.3788/gzxb20215003.0311003Su Jie, Zhai Aiping, Zhao Wenjing, et al. Hadamard single-pixel imaging using adaptive oblique zigzag sampling[J]. Acta Photonica Sinica, 2021, 50: 0311003 doi: 10.3788/gzxb20215003.0311003 [21] Gan Lu. Block compressed sensing of natural images[C]//2007 15th International Conference on Digital Signal Processing. Cardiff: IEEE, 2007: 403-406. [22] Van Trinh C, Dinh K Q, Jeon B. Edge-preserving block compressive sensing with projected Landweber[C]//2013 20th International Conference on Systems, Signals and Image Processing (IWSSIP). Bucharest: IEEE, 2013: 71-74. [23] 张赛文, 于斌, 陈丹妮, 等. 基于压缩感知的高密度分子定位算法比较[J]. 中国激光, 2018, 45:0307014 doi: 10.3788/CJL201845.0307014Zhang Saiwen, Yu Bin, Chen Danni, et al. Comparison of algorithms of high-density molecule localization based on compressed sensing[J]. Chinese Journal of Lasers, 2018, 45: 0307014 doi: 10.3788/CJL201845.0307014 [24] 吴光文, 张爱军, 王昌明. 一种用于压缩感知理论的投影矩阵优化算法[J]. 电子与信息学报, 2015, 37(7):1682-1687 doi: 10.11999/JEIT141450Wu Guangwen, Zhang Aijun, Wang Changming, et al. Novel optimization method for projection matrix in compress sensing theory[J]. Journal of Electronics & Information Technology, 2015, 37(7): 1682-1687 doi: 10.11999/JEIT141450 [25] Li Shufeng, Cao Guangjing, Wei Shanshan. Improved measurement matrix and reconstruction algorithm for compressed sensing[C]//2018 8th International Conference on Electronics Information and Emergency Communication (ICEIEC). 2018: 136-139. [26] Wan Rentao, Zhou Jinjia, Huang Bowen, et al. APMC: adjacent pixels based measurement coding system for compressively sensed images[J]. IEEE Transactions on Multimedia, 2021, 24: 3558-3569. [27] Kuusela T A. Single-pixel camera[J]. American Journal of Physics, 2019, 87(10): 846-850. doi: 10.1119/1.5122745 [28] 王之润, 赵文静, 翟爱平, 等. 不同正交变换深度Q网络单像素成像性能比较[J]. 光子学报, 2022, 51:0311003 doi: 10.3788/gzxb20225103.0311003Wang Zhirun, Zhao Wenjing, Zhai Aiping, et al. Comparison on performance of deep Q network based single-pixel imaging using different orthogonal transformations[J]. Acta Photonica Sinica, 2022, 51: 0311003 doi: 10.3788/gzxb20225103.0311003 [29] Sun Mingjie, Xu Zihao, Wu Ling’an. Collective noise model for focal plane modulated single-pixel imaging[J]. Optics and Lasers in Engineering, 2018, 100: 18-22. doi: 10.1016/j.optlaseng.2017.07.005 -





 下载:
下载:




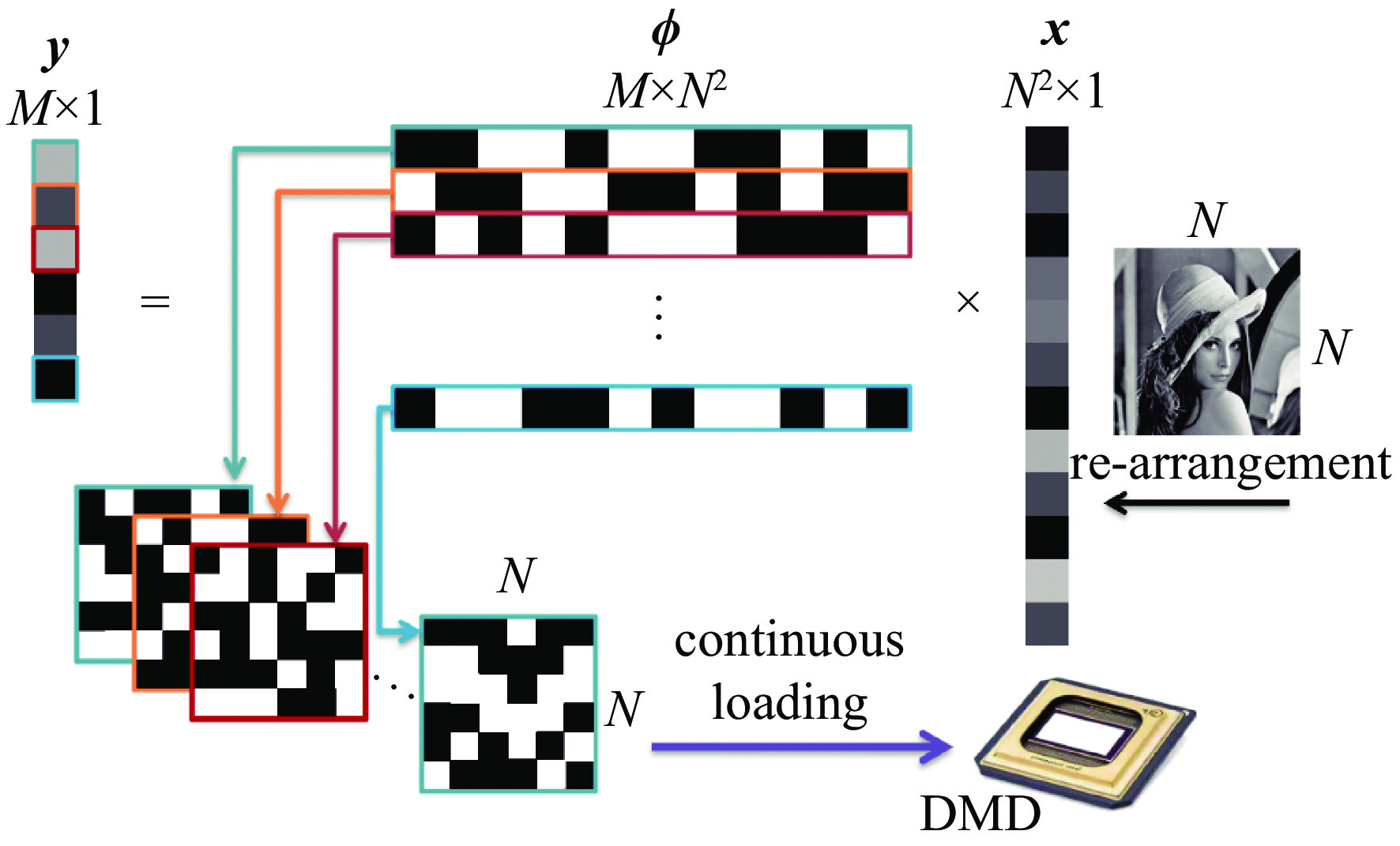
 下载:
下载: