基于Kriging模型的水中放电沉积能量优化分析

赵景林; 王志强; 王进君; 张东东; 李国锋

doi:10.11884/HPLPB202335.220240

基于Kriging模型的水中放电沉积能量优化分析

doi: 10.11884/HPLPB202335.220240

大连理工大学电气工程学院，辽宁大连 116024

基金项目: 国家自然科学基金项目(51607023)；辽宁省科学技术计划项目（2021-BS-293）

详细信息

作者简介:
赵景林，2855806591@qq.com

通讯作者:
王志强，wangzq@dlut.edu.cn

中图分类号: TM89
计量
- 文章访问数: 623
- HTML全文浏览量: 266
- PDF下载量: 68
- 被引次数: 0
出版历程
- 收稿日期: 2022-08-05
- 修回日期: 2022-10-12
- 录用日期: 2022-10-14
- 网络出版日期: 2022-10-18
- 刊出日期: 2023-03-01

Deposited energy optimization analysis of discharge in water based on Kriging model

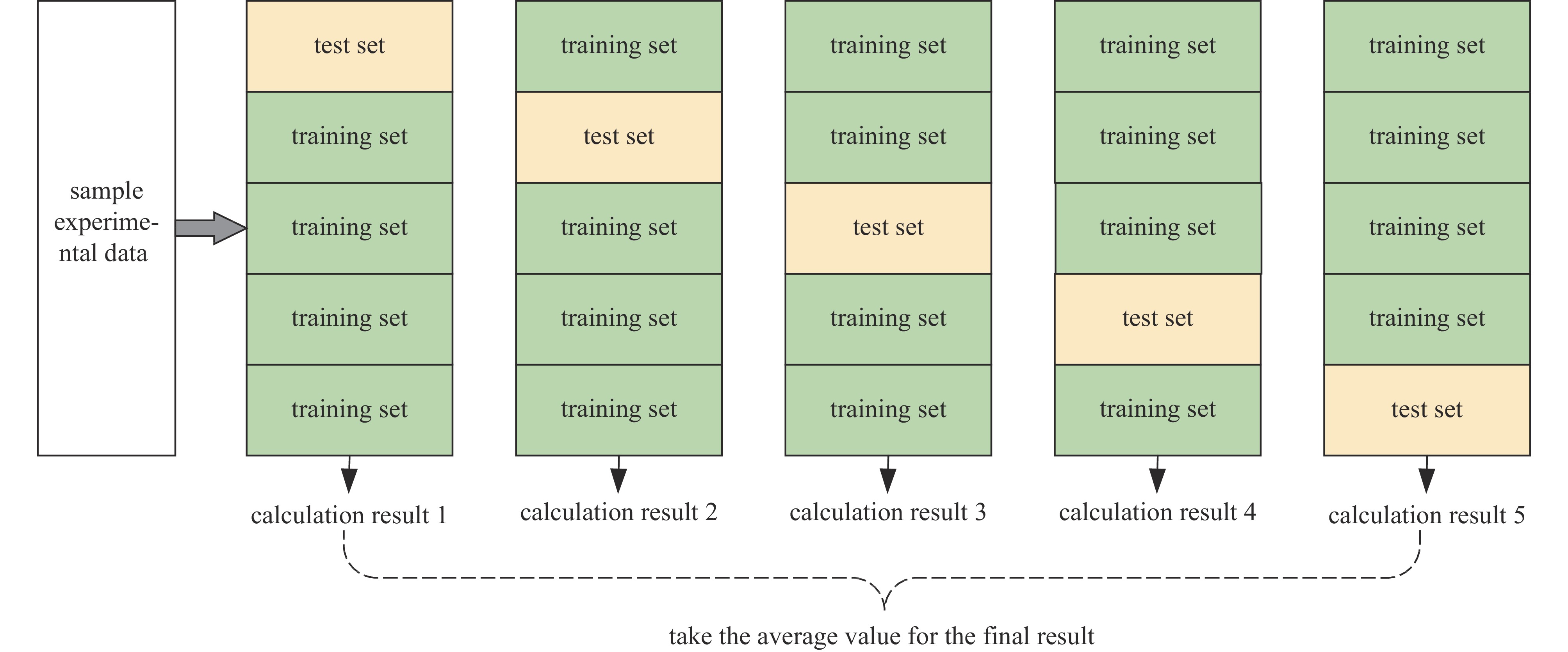
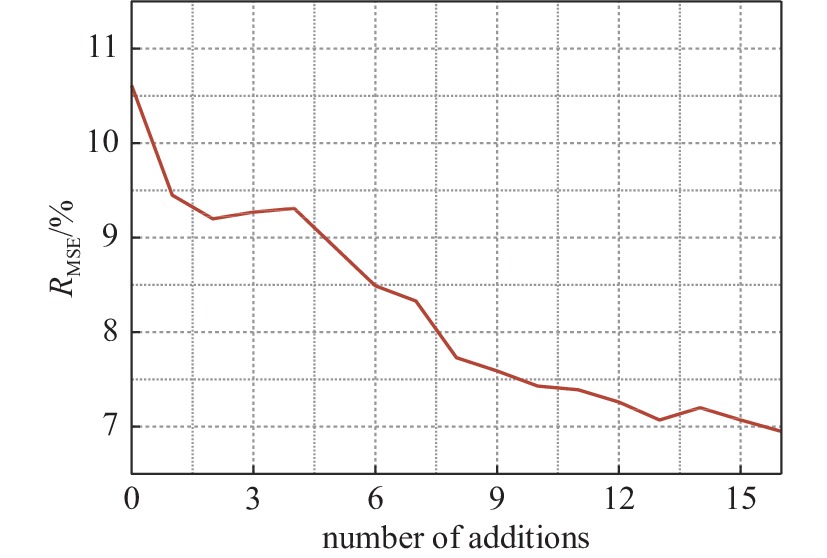
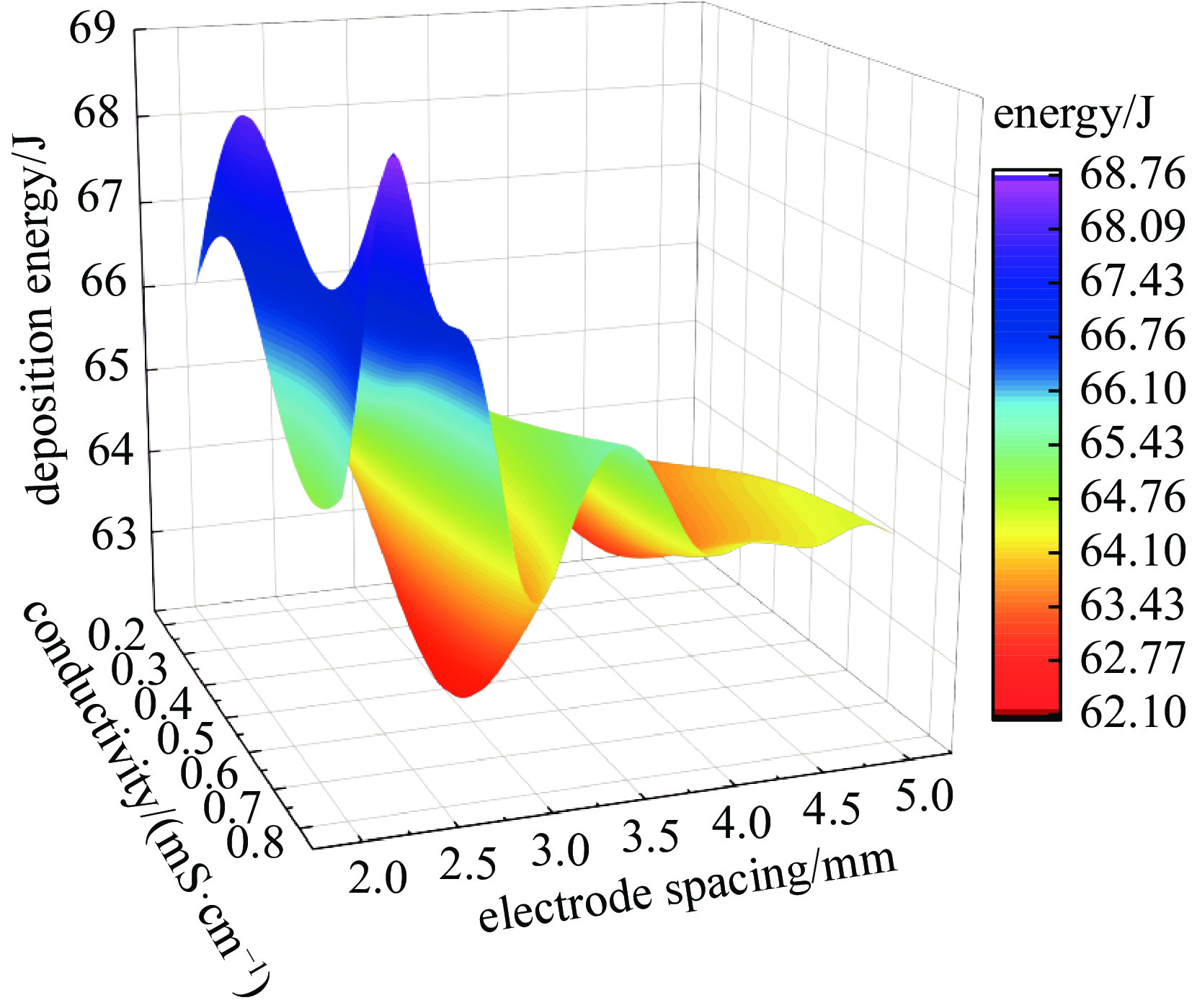
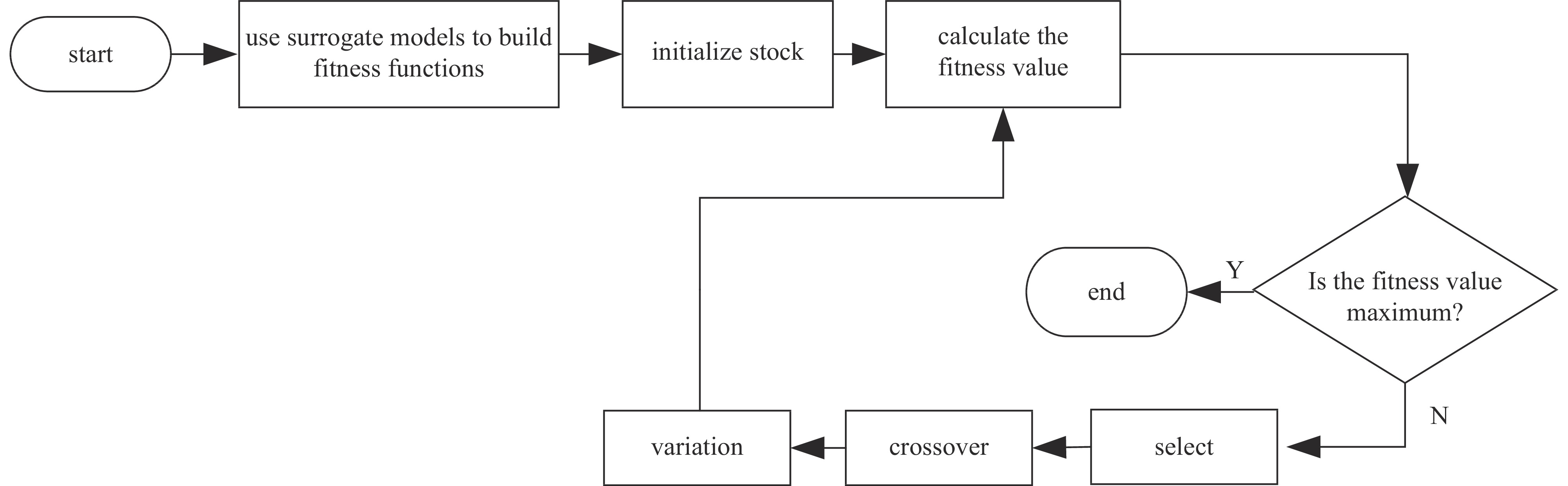
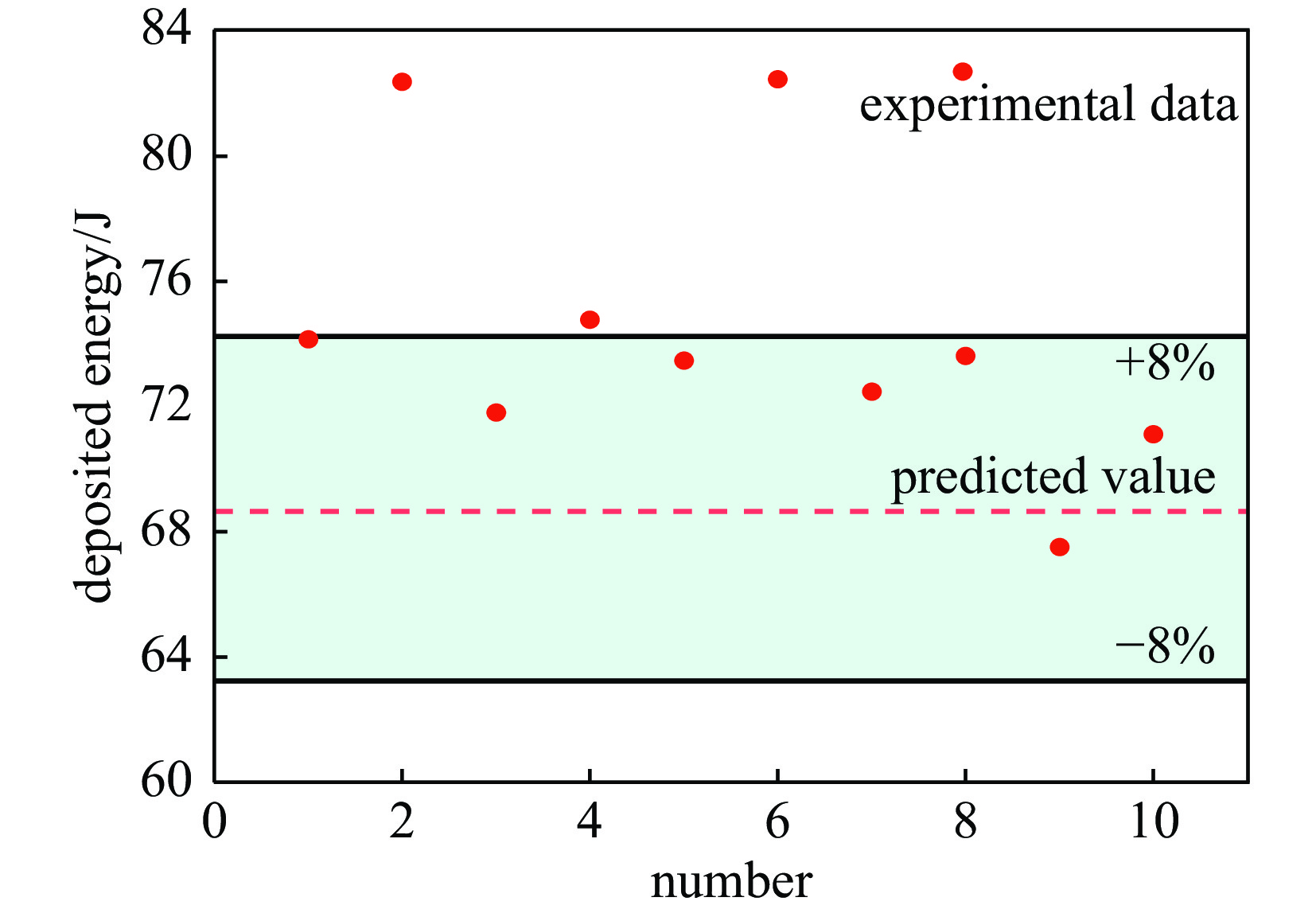
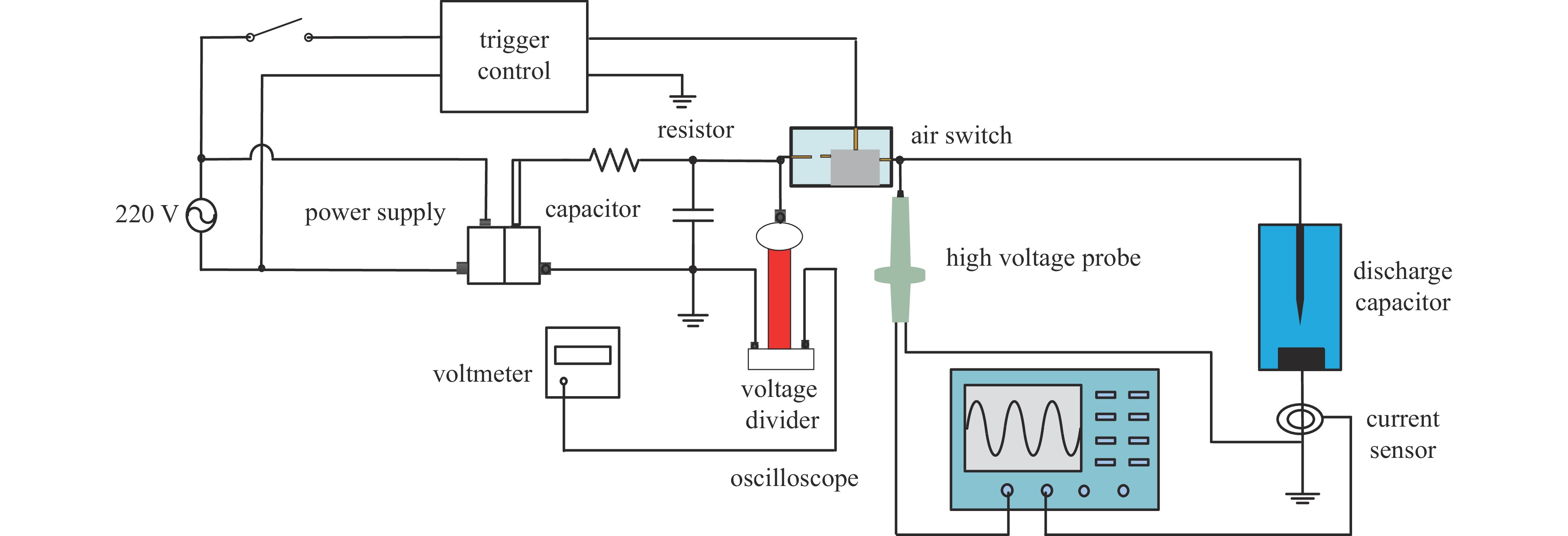
College of Electrical Engineering, Dalian University of Technology, Liaoning Dalian 116024

摘要

摘要: 水中脉冲放电过程较为复杂，放电参数与放电沉积能量之间没有明确的函数关系。为了获得最佳沉积能量，明晰不同放电参数相互作用对沉积能量的影响，获得最佳放电参数组合，本文搭建了水中高压脉冲放电实验平台，结合Kriging代理模型探究了电压、电极间距和电导率三种放电参数对水中放电沉积能量的影响；利用遗传算法进行全局寻优，确定了最佳放电参数组合。研究结果表明：通过交叉验证评估该模型的均方根误差为6.95%，满足精度要求；外加电压一定时，在电极间距和电导率的协同作用下，沉积能量的变化呈现多峰值特性；在电压、电极间距和电导率分别为17 kV、2.28 mm和0.8 mS/cm的条件下产生的沉积能量最大，为最佳参数组合；通过实验验证了在最佳点的预测值和实际值相对偏差在8%以内。
- 水中放电 /
- 代理模型 /
- 沉积能量 /
- 放电参数 /
- 交叉验证
Abstract: The pulsed discharge process in water is complex and there is no clear functional relationship between the discharge parameters and the discharge deposition energy. To obtain the optimum deposition energy, clarify the influence of different discharge parameters on the deposition energy and obtain the best combination of discharge parameters, this paper builds a high-voltage pulse discharge test platform in water and investigates the influence of three discharge parameters, namely voltage, electrode spacing and conductivity, on the deposition energy of discharge in water by combining with the Kriging agent model. The optimal combination of discharge parameters was determined by using a genetic algorithm. The results of the study show that: the root mean square error of the model is 6.95%, which satisfies the accuracy requirement through cross-validation; the deposition energy varies with multiple peaks under the synergistic effect of electrode spacing and conductivity at a certain applied voltage; the best combination of voltage, electrode spacing and conductivity is 17 kV, 2.28 mm and 0.8 mS/cm respectively, which produces the highest deposition energy. The relative deviation between predicted and actual values at the optimum point were experimentally verified to be within 8%.
- discharge in water /
- surrogate model /
- deposited energy /
- discharge parameters /
- cross validation

HTML全文

图 1 水中高压脉冲放电实验平台示意图

Figure 1. Schematic diagram of underwater high-voltage pulse discharge experiment system

下载: 全尺寸图片幻灯片

图 2 水中高压脉冲放电典型电压电流波形图

Figure 2. Typical voltage and current waveform of high voltage pulse discharge in water

下载: 全尺寸图片幻灯片

图 3 流注发展过程

Figure 3. Plasma channel development process

下载: 全尺寸图片幻灯片

图 4 沉积能量的计算结果图

Figure 4. Results of deposited energy calculation

下载: 全尺寸图片幻灯片

图 5 优化设计流程图

Figure 5. Flowchart of the optimization search analysis

下载: 全尺寸图片幻灯片

图 6 20个初始样本点的空间分布

Figure 6. Spatial distribution of the 20 initial sample points

下载: 全尺寸图片幻灯片

图 7 交叉验证计算过程

Figure 7. Cross-validation of the computational process

下载: 全尺寸图片幻灯片

图 8 均方根误差随加点次数的变化

Figure 8. Variation of root mean square error with the number of additions

下载: 全尺寸图片幻灯片

图 9 沉积能量的多峰值特性

Figure 9. Multi-peak characteristics of deposited energy

下载: 全尺寸图片幻灯片

图 10 全局寻优流程图

Figure 10. Global optimization search flow chart

下载: 全尺寸图片幻灯片

图 11 实验结果与最优值的对比

Figure 11. Comparison between experimental results and optimal deposited energy

下载: 全尺寸图片幻灯片

表 1 实验变量及其范围

Table 1. Experimental variables and their scope

voltage/kV	electrode spacing/mm	conductivity/(mS·cm⁻¹)
13−17	2−5	0.2−0.8

下载: 导出CSV

表 2 反归一化后的部分初始样本点及对应的实验结果

Table 2. Some of the initial sample points after inverse normalization and the corresponding experimental results

voltage/kV	conductivity/(mS·cm⁻¹)	electrode spacing/mm	deposited energy/J
14.1	0.26	4.53	40.46
13.4	0.77	4.37	26.00
16.2	0.33	2.16	62.3
15.1	0.45	4.68	46.87
15.7	0.64	2.32	51.81
14.5	0.52	2.00	41.74
13.8	0.39	2.79	40.09
16.8	0.55	2.95	59.76

下载: 导出CSV

表 3 反归一化后的部分新增点及对应的实验结果

Table 3. After the normalization of some of the new points and the corresponding experimental results

voltage/kV	conductivity/(mS·cm⁻¹)	electrode spacing/mm	deposited energy/J
17	0.331	2.28	67.41
17	0.425	2	66.78
17	0.2	2.04	66.51
17	0.8	3.5	65.6
17	0.65	2.19	66.93

下载: 导出CSV

表 4 不同电导率下，电极间距变化对沉积能量的影响

Table 4. Effect of electrode spacing variation on deposited energy at different conductivities

conductivity/(mS·cm⁻¹)	spacing variation Δd/mm	deposited energy variation/J
0.2	4	17.59
0.4	4	5.04
0.6	4	8.96
0.8	4	13.56
1	4	11.4

下载: 导出CSV

表 5 模型的全局最优解

Table 5. Global optimal solution of the model

voltage/kV	conductivity/(mS·cm⁻¹)	electrode spacing/mm	optimal deposited energy/J
17	0.8	2.28	68.73

下载: 导出CSV

参考文献(26)

[1]	尤特金. 液电效应[M]. 北京: 科学出版社, 1962: 1-2 Yutkin. Electro-hydraulic effect[M]. Beijing: Science Press, 1962: 1-2
[2]	于海平, 郑秋丽, 安云雷. 电液成形技术研究现状及发展趋势[J]. 精密成形工程, 2017, 9(3):65-72 doi: 10.3969/j.issn.1674-6457.2017.03.013 Yu Haiping, Zheng Qiuli, An Yunlei. Research status and development tendency of electrohydraulic forming (EHF) technology[J]. Journal of Netshape Forming Engineering, 2017, 9(3): 65-72 doi: 10.3969/j.issn.1674-6457.2017.03.013
[3]	王志强, 曹云霄, 邢政伟, 等. 高压脉冲放电破碎菱镁矿石的实验研究[J]. 电工技术学报, 2019, 34(4):863-870 Wang Zhiqiang, Cao Yunxiao, Xing Zhengwei, et al. Experimental study on fragmentation of magnesite ores by pulsed high-voltage discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 863-870
[4]	李沼萱, 闫铁, 侯兆凯, 等. 液相高压脉冲放电致裂岩石技术研究进展[J]. 特种油气藏, 2021, 28(4):1-9 doi: 10.3969/j.issn.1006-6535.2021.04.001 Li Zhaoxuan, Yan Tie, Hou Zhaokai, et al. Study progress of rock fracturing technology with high-voltage pulse discharge in liquid[J]. Special Oil & Gas Reservoirs, 2021, 28(4): 1-9 doi: 10.3969/j.issn.1006-6535.2021.04.001
[5]	付荣耀, 孙鹞鸿, 樊爱龙, 等. 高压电脉冲在页岩气开采中的压裂实验研究[J]. 强激光与粒子束, 2016, 28:079001 doi: 10.11884/HPLPB201628.079001 Fu Rongyao, Sun Yaohong, Fan Ailong, et al. Research of rock fracturing based on high voltage pulse in shale gas drilling[J]. High Power Laser and Particle Beams, 2016, 28: 079001 doi: 10.11884/HPLPB201628.079001
[6]	Li Xiandong, Liu Yi, Liu Siwei, et al. Influence of deposited energy on shock wave induced by underwater pulsed current discharge[J]. Physics of Plasmas, 2016, 23: 103104. doi: 10.1063/1.4964663
[7]	刘毅, 李志远, 李显东, 等. 水中大电流脉冲放电激波影响因素分析[J]. 中国电机工程学报, 2017, 37(9):2741-2749 Liu Yi, Li Zhiyuan, Li Xiandong, et al. Effect factors of the characteristics of shock waves induced by underwater high current pulsed discharge[J]. Proceedings of the CSEE, 2017, 37(9): 2741-2749
[8]	童得恩, 朱鑫磊, 邹晓兵, 等. 水中放电预加热过程的数值模拟研究[J]. 高电压技术, 2019, 45(5):1461-1467 Tong De’en, Zhu Xinlei, Zou Xiaobing, et al. Numerical simulation of the preheating process of pulse discharge in water[J]. High Voltage Engineering, 2019, 45(5): 1461-1467
[9]	卞文娟, 周明华, 雷乐成. 高压脉冲液相放电降解水中邻氯苯酚[J]. 化工学报, 2005, 56(1):152-156 doi: 10.3321/j.issn:0438-1157.2005.01.028 Bian Wenjuan, Zhou Minghua, Lei Lecheng. Degradation of o-CP by pulsed high voltage discharge in water[J]. Journal of Chemical Industry and Engineering (China), 2005, 56(1): 152-156 doi: 10.3321/j.issn:0438-1157.2005.01.028
[10]	Rond C, Desse J M, Fagnon N, et al. Influence of applied voltage and electrical conductivity on underwater pin-to-pin pulsed discharge[J]. Journal of Physics D: Applied Physics, 2019, 52: 025202. doi: 10.1088/1361-6463/aae681
[11]	Zingerman Z. Pressure on the shockwave front from the slope impulse energy in an electric discharge[J]. Zhurnal Tekhnicheskoi Fiziki (Journal of Technical Physics), 1956, 26(11): 2539-2540.
[12]	Liu Yi, Li Zhiyuan, Li Xiandong, et al. Intensity improvement of shock waves induced by liquid electrical discharges[J]. Physics of Plasmas, 2017, 24: 043510. doi: 10.1063/1.4980848
[13]	喻越, 朱鑫磊, 黄昆, 等. 应用于石油解堵增产的水中脉冲放电特性实验研究[J]. 高电压技术, 2020, 46(8):2951-2959 Yu Yue, Zhu Xinlei, Huang Kun, et al. Experimental study on pulse discharge characteristics in water applied to oil plugging and increasing production[J]. High Voltage Engineering, 2020, 46(8): 2951-2959
[14]	吴敏干, 刘毅, 林福昌, 等. 液电脉冲激波特性分析[J]. 强激光与粒子束, 2020, 32:045002 doi: 10.11884/HPLPB202032.190356 Wu Min’gan, Liu Yi, Lin Fuchang, et al. Characteristics analysis of electrohydraulic shockwave[J]. High Power Laser and Particle Beams, 2020, 32: 045002 doi: 10.11884/HPLPB202032.190356
[15]	黄海, 雷开卓, 黄建国. 水下等离子体声源的正交试验设计与分析[J]. 声学技术, 2012, 31(4):381-384 doi: 10.3969/j.issn.1000-3630.2012.04.008 Huang Hai, Lei Kaizhuo, Huang Jianguo. The orthogonal experimental design and analysis of underwater plasma sound source[J]. Technical Acoustics, 2012, 31(4): 381-384 doi: 10.3969/j.issn.1000-3630.2012.04.008
[16]	李元, 温嘉烨, 李林波, 等. 液体介质微/纳秒脉冲放电的特性与机理: 现状及进展[J]. 强激光与粒子束, 2021, 33:065001 Li Yuan, Wen Jiaye, Li Linbo, et al. Characteristics and mechanisms of streamer discharge in liquids under micro/nano-second pulsed voltages: status and advances[J]. High Power Laser and Particle Beams, 2021, 33: 065001
[17]	Li Bin, Xue Sheng, Yuan Liang. Experimental study on pressure wave characteristics of high-voltage discharge in water with hemispherical electrodes[J]. IEEE Access, 2021, 9: 87173-87181. doi: 10.1109/ACCESS.2021.3075488
[18]	邢政伟, 王志强, 曹云霄, 等. 水中脉冲电弧放电等离子体通道直接冲击压力特性[J]. 高电压技术, 2019, 45(3):832-838 Xing Zhengwei, Wang Zhiqiang, Cao Yunxiao, et al. Direct impact pressure characteristics of pulsed arc discharge plasma channel in water[J]. High Voltage Engineering, 2019, 45(3): 832-838
[19]	刘毅, 吴敏干, 林福昌, 等. 液电脉冲激波碎煤能量转换效率分析[J]. 煤炭科学技术, 2021, 49(12):217-224 Liu Yi, Wu Min’gan, Lin Fuchang, et al. Analysis of energy conversion efficiency of coal crushed by hydroelectric pulse shock wave[J]. Coal Science and Technology, 2021, 49(12): 217-224
[20]	李显东, 刘毅, 李志远, 等. 不均匀电场下水中脉冲放电观测及沉积能量对激波的影响[J]. 中国电机工程学报, 2017, 37(10):3028-3036 Li Xiandong, Liu Yi, Li Zhiyuan, et al. Observation of underwater pulse discharge and influence of deposited energy on shock wave in non-uniform electric field[J]. Proceedings of the CSEE, 2017, 37(10): 3028-3036
[21]	王林涛, 栾鹏龙, 孙伟, 等. 盾构推进液压系统参数优化[J]. 机械设计与制造, 2021(7):54-57 doi: 10.3969/j.issn.1001-3997.2021.07.013 Wang Lintao, Luan Penglong, Sun Wei, et al. Parameter optimization of shield propulsion hydraulic system[J]. Machinery Design & Manufacture, 2021(7): 54-57 doi: 10.3969/j.issn.1001-3997.2021.07.013
[22]	Forrester A I J, Sóbester A, Keane A J. Engineering design via surrogate modelling: a practical guide[M]. Southern Gate: John Wiley & Sons Ltd. , 2008: 37-104.
[23]	Lv Zhaoyan, Lu Zhenzhou, Wang Pan. A new learning function for Kriging and its applications to solve reliability problems in engineering[J]. Computers & Mathematics with Applications, 2015, 70(5): 1182-1197.
[24]	汪学清, 刘爽, 李秋燕, 等. 基于K折交叉验证的SVM隧道围岩分级判别[J]. 矿冶工程, 2021, 41(6):126-128,133 doi: 10.3969/j.issn.0253-6099.2021.06.031 Wang Xueqing, Liu Shuang, Li Qiuyan, et al. Classification and discrimination of surrounding rock of tunnel based on SVM of K-fold cross validation[J]. Mining and Metallurgical Engineering, 2021, 41(6): 126-128,133 doi: 10.3969/j.issn.0253-6099.2021.06.031
[25]	Zhan Dawei, Xing Huanlai. Expected improvement for expensive optimization: a review[J]. Journal of Global Optimization, 2020, 78(3): 507-544. doi: 10.1007/s10898-020-00923-x
[26]	李显东. 不均匀电场下水中微秒脉冲放电过程及机理研究[D]. 武汉: 华中科技大学, 2018: 8-10 Li Xiandong. Research on process and mechanism of underwater microsecond pulsed discharges under nonuniform electric fields[D]. Wuhan: Huazhong University of Science and Technology, 2018: 8-10