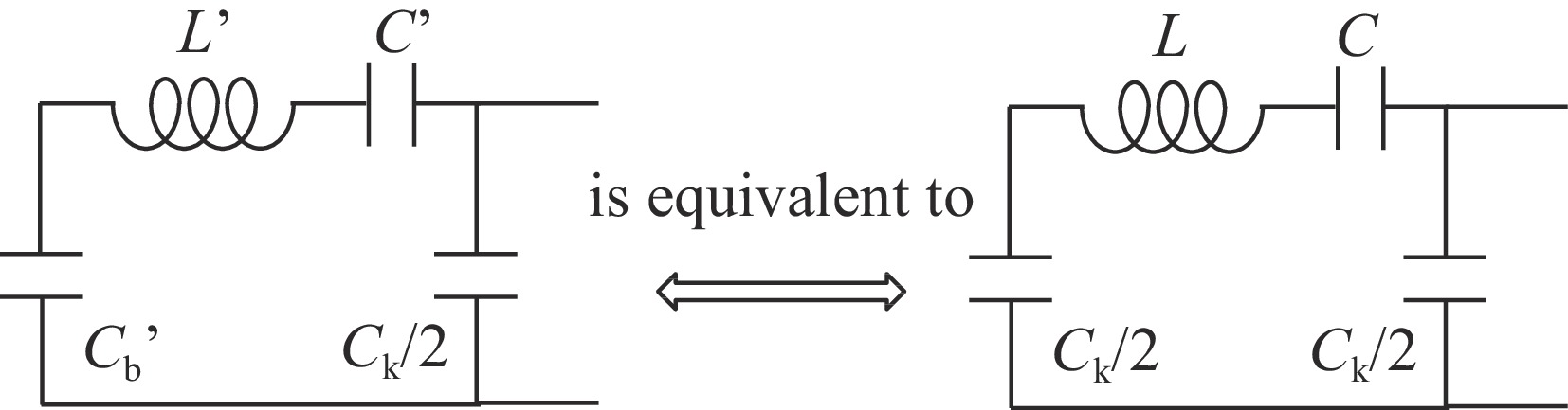Simulation studies on the field flatness tuning of multi-cell superconducting radio-frequency cavities
-
摘要:
简述了用于分析多胞超导射频腔场平坦度调节的微扰理论，推导了场平坦度的理论计算方法。针对超导腔微小范围内的纵向拉伸/挤压，进行理论计算分析与结构-电磁多物理场模拟计算以求得变形前后腔体场平坦度及其变化趋势，所得结果表明：理论分析结果与仿真计算结果基本一致，进一步深入验证了该微扰理论的有效性。在多胞超导射频腔的加工制造、运行过程中的关键环节，国际上广泛采用的两种方法——包括预调谐过程中的“先单胞后整腔”和运行时腔体调谐过程中“整腔拉伸/挤压”方法，基于分析结果，这两种方法正确性和合理性均在理论上得以验证。在超导射频腔腔型设计的第一阶段——单胞优化设计过程中加入结构-电磁多物理场分析，可使腔型优化设计过程更加高效，结果表明：优化后的单胞（包括端胞和中间胞）的频率敏感度应尽可能接近或相等，以保证在腔变形期间始终保持较好的场平坦度。
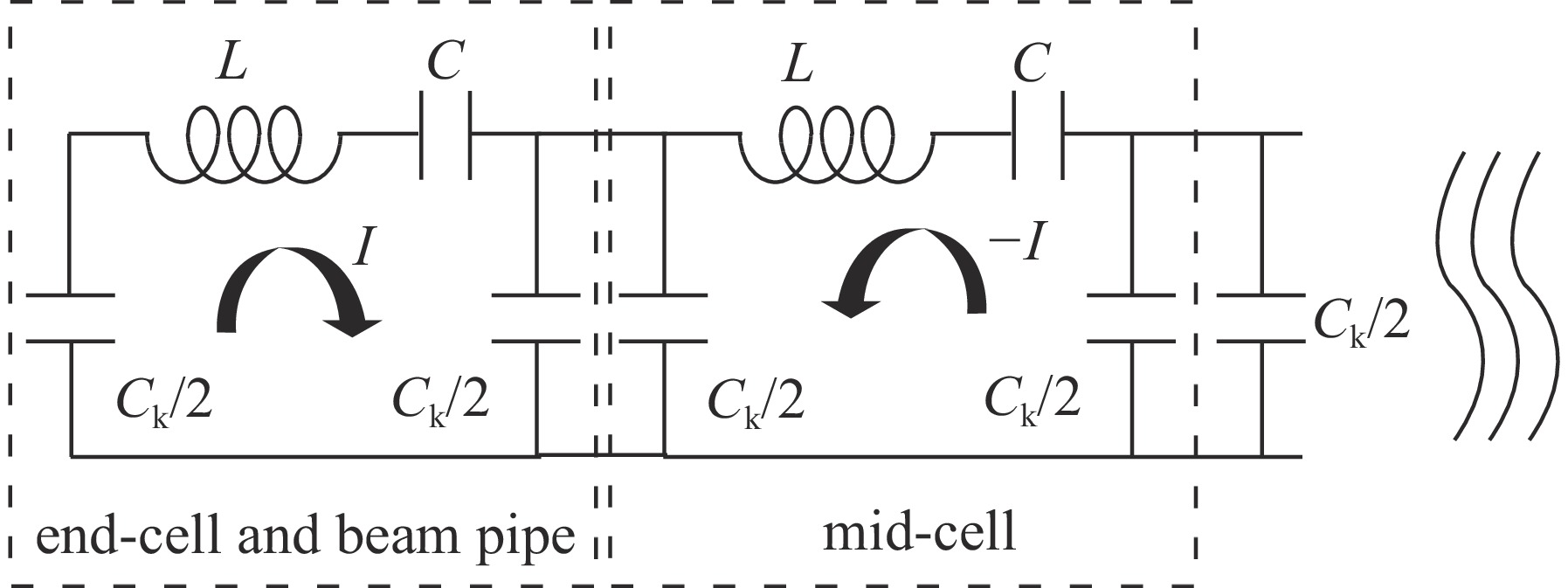
Abstract:Perturbation theory of multi-cell superconducting radio-frequency (SRF) cavities, which is widely used in analysis of field flatness adjustment, is briefly described, and theoretical calculation method of field flatness is deduced. Multi-field coupled simulation calculations are performed for resonant cavities with minor longitudinal deformation, the field flatness and its trend with deformation quantity are obtained. For two widely adopted methods for SRF cavity development, including ‘first-single-then-the-whole pre-tuning’ and ‘whole-cavity stretching/squeezing’ during tuning process, theoretical analysis is carried out based on the capacitively coupled LC oscillator model of perturbation theory for multi-cell cavities, and meanwhile further verifying multi-field coupled simulation calculations are performed by combination of CST MWS and ANSYS for three typical SRF 9-cell cavities - for main Linac of XFEL, TRIUMF e-Linac, and for injector of SHINE as a candidate. It is shown that theoretical analysis results and simulation results are perfectly consistent with each other. The validity and feasibility of the two widely adopted methods above are verified and proved to be correct in the scope of perturbation. Cavity shape structure with excellent acceleration performance and field flatness can be obtained just by adding multi-physics field analysis to the optimization design of single-cell, which makes the design process of cavity shape more efficient. It is illustrated that the tuning sensitivity factors of optimized single-cells including end-cells and mid-cell should be as close or equal as possible to maintain field-flatness during cavity deformation.
-
图 1 含束管N胞射频腔的等效电路模型
Figure 1. The model of equivalent circuit for N-cell cavity with beam tubes
图 2 工作于具有理想平坦度的π模基模场条件下的N胞射频腔等效电路
Figure 2. The model of equivalent circuit for N-cell cavity operating in fundamental π-mode with ideal field flatness
图 3 N胞射频腔端腔胞及束管等效电路的等效变换
Figure 3. Equivalent transformation of the models of equivalent circuit for end-cell and tube of N-cell cavity
图 4 不同的A=B时，场平坦度随中间腔胞微扰的变化规律
Figure 4. Field flatness F variation with minor perturbation emid of cell capacity, given different A=B
图 5 不同中间腔胞微扰
$ {e}_{\mathrm{m}\mathrm{i}\mathrm{d}} $ 、B=0.5情况下，场平坦度随A的变化规律Figure 5. Field flatness F variation with A, given B=0.5, for different minor perturbation of mid-cell emid
图 7 无加强筋和有加强筋的1.3 GHz 9-cell裸腔结构示意图
Figure 7. Structure diagram of 1.3 GHz 9-cell superconducting radio-frequency cavities without/with enhancement rings
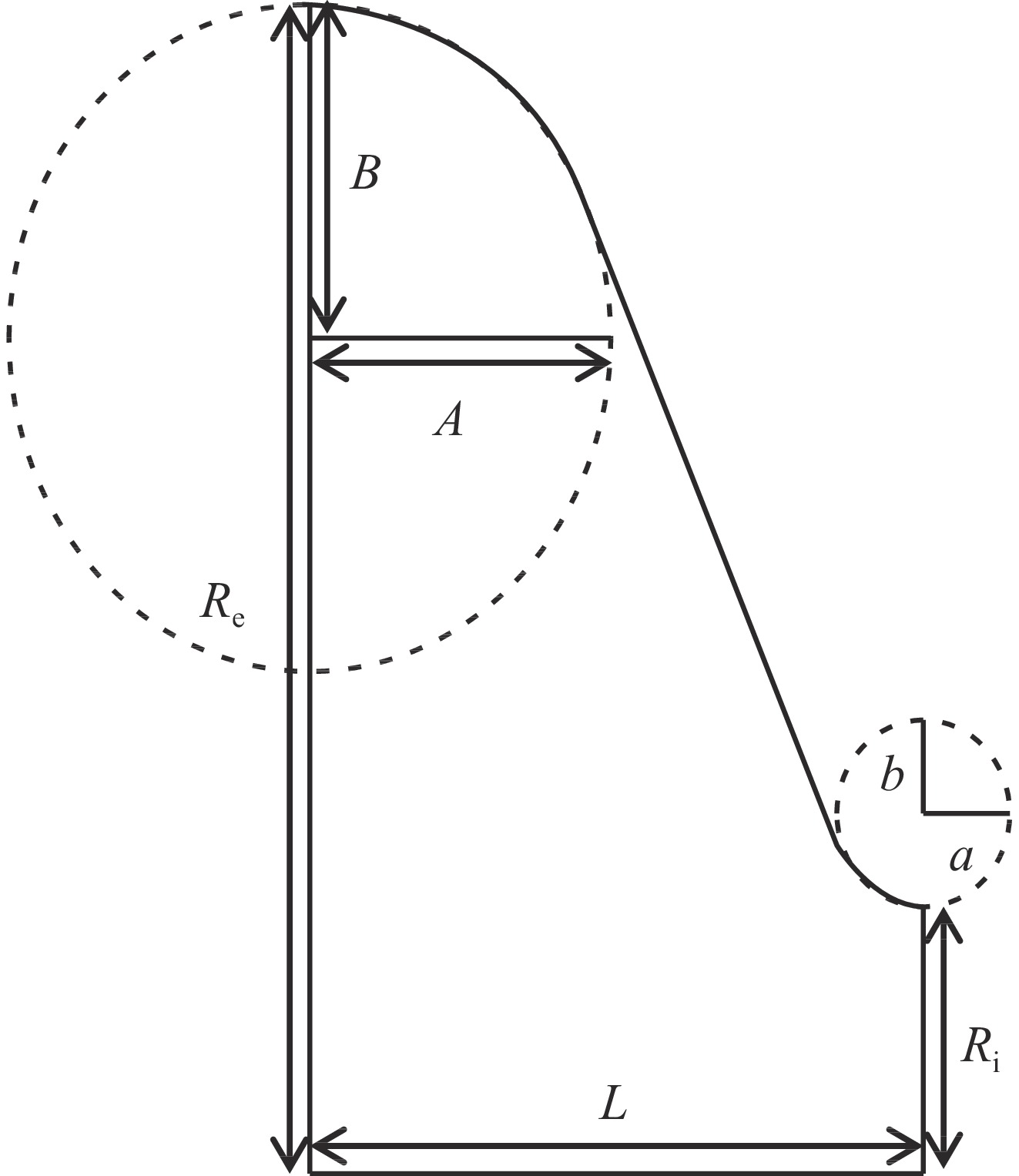
表 1 XFEL的主直线加速器、TRIUMF 电子直线加速器和用于SHINE 的注入器候选的1.3 GHz 9-cell腔型结构参数尺寸
Table 1. Geometry parameters of three types of 1.3 GHz 9-cell cavities for main LINAC of XFEL, TRIUMF e-Linac, and for injector of SHINE as a candidate
Types of cavity cell Re/mm Ri/mm A/mm B/mm a/mm b/mm L/mm Middle half-cell XFEL 103.3 35.0 42.0 42.0 12.0 19.0 57.7 TRIUMF 103.3 35.0 42.0 42.0 12.0 19.0 57.7 SHINE 103.3 35.0 42.0 42.0 12.0 19.0 57.7 Pick-up side
half-cellXFEL 103.3 39.0 42.0 42.0 9.0 12.8 56.7 TRIUMF 103.3 39.0 42.0 42.0 9.0 12.8 56.7 SHINE 103.3 39.0 42.0 42.0 9.0 12.8 56.7 Coupler side
half-cellXFEL 103.3 39.0 40.34 40.34 10.0 13.5 55.7 TRIUMF 103.3 48.0 45.0 40.5 10.0 13.5 56.0 SHINE 103.3 55.0 48.9 36.7 9.0 12.8 58.1 
下载: 导出CSV
表 3 不同调谐力对应的三种无加强筋1.3 GHz 9-cell腔型结构的腔胞微扰量理论计算值
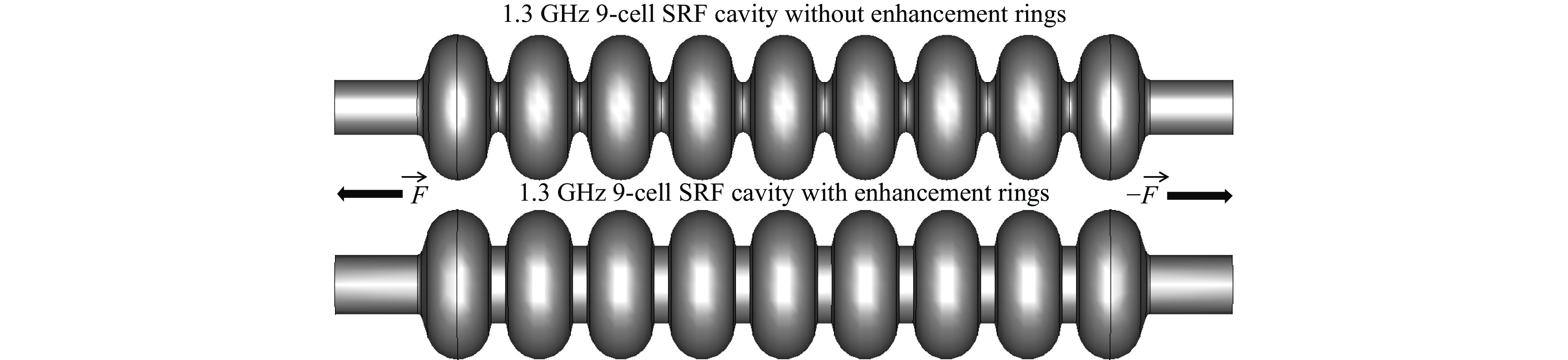
Table 3. Minor perturbations due to different tuning force for XFEL, TRIUMF and SHINE candidate 1.3 GHz 9-cell SRF cavities without enhancement rings
Tuning force/kN (squeezed) emid/105 eend1/105 eend2/105 0, undeformed XFEL 0 0 0 TRIUMF 0 0 0 SHINE 0 0 0 2, deformed XFEL 4.877 4.149 4.149 TRIUMF 4.877 4.149 4.133 SHINE 4.877 4.149 3.062 4, deformed XFEL 10.327 7.946 7.946 TRIUMF 10.327 7.946 7.931 SHINE 10.327 7.946 5.894
下载: 导出CSV
表 6 不同调谐力对应的三种有加强筋1.3 GHz 9-cell腔型结构的腔胞微扰量理论计算值
Table 6. Minor perturbations due to different tuning force for XFEL, TRIUMF and SHINE candidate 1.3 GHz 9-cell SRF cavities with enhancement rings
Tuning force/kN (squeezed) emid/105 eend1/105 eend2/105 0, undeformed XFEL 0 0 0 TRIUMF 0 0 0 SHINE 0 0 0 2, deformed XFEL 2.526 2.620 2.620 TRIUMF 2.526 2.620 2.796 SHINE 2.526 2.620 3.326 4, deformed XFEL 5.208 5.485 5.485 TRIUMF 5.208 5.485 5.610 SHINE 5.208 5.485 6.668 6, deformed XFEL 7.820 8.333 8.333 TRIUMF 7.820 8.333 8.441 SHINE 7.820 8.333 10.028
下载: 导出CSV
表 2 不同调谐力对三种无加强筋1.3 GHz 9-cell腔型结构腔胞0模与π模谐振频率的影响
Table 2. Variation of resonant frequency due to different tuning force for XFEL, TRIUMF and SHINE 1.3 GHz 9-cell SRF cavities without enhancement rings
Tuning force/kN (squeezed) Types of cavity cell Resonant frequency/MHz 0-mode π-mode 0, undeformed Middle half-cell XFEL 1275.748 1300 TRIUMF 1275.748 1300 SHINE 1275.748 1300 Pick-up side half-cell with beam pipe XFEL 1287.78 1300 TRIUMF 1287.78 1300 SHINE 1287.78 1300 Coupler side half-cell with beam pipe XFEL 1287.78 1300 TRIUMF 1288.136 1300 SHINE 1288.827 1300 2, deformed Middle half-cell XFEL 1275.468 1299.745 TRIUMF 1275.468 1299.745 SHINE 1275.468 1299.745 Pick-up side half-cell with beam pipe XFEL 1287.544 1299.78 TRIUMF 1287.544 1299.78 SHINE 1287.544 1299.78 Coupler side half-cell with beam pipe XFEL 1287.544 1299.78 TRIUMF 1287.901 1299.781 SHINE 1288.653 1299.836 4, deformed Middle half-cell XFEL 1275.155 1299.569 TRIUMF 1275.155 1299.569 SHINE 1275.155 1299.569 Pick-up side half-cell with beam pipe XFEL 1287.328 1299.574 TRIUMF 1287.328 1299.574 SHINE 1287.328 1299.574 Coupler side half-cell with beam pipe XFEL 1287.328 1299.574 TRIUMF 1287.685 1299.574 SHINE 1288.492 1299.68
下载: 导出CSV
表 4 不同调谐力对应的三种无加强筋1.3 GHz 9-cell射频腔场平坦度的理论计算值与仿真计算值结果对比
Table 4. Results comparison of field flatness between theoretical and simulation calculations for XFEL, TRIUMF and SHINE 1.3 GHz 9-cell SRF cavities without enhancement rings
Tuning force/kN (squeezed) F, (Field flatness) Theoretical calculation value Simulation calculation value 0, undeformed XFEL 100% 99.95% TRIUMF 100% 99.94% SHINE 100% 99.92% 2, deformed XFEL 98.79% 97.7% TRIUMF 98.74% 97.6% SHINE 95.35% 93.9% 4, deformed XFEL 96.03% 96.8% TRIUMF 95.99% 96.7% SHINE 89.86% 89.0%
下载: 导出CSV
表 5 不同调谐力对三种有加强筋1.3 GHz 9-cell腔型结构腔胞0模与π模谐振频率的影响
Table 5. Variation of resonant frequency due to different tuning force for XFEL, TRIUMF and SHINE 1.3 GHz 9-cell SRF cavities with enhancement rings
Tuning force/kN (squeezed) Types of cavity cell Resonant frequency/MHz 0-mode π-mode 0, undeformed Middle half-cell XFEL 1275.748 1300 TRIUMF 1275.748 1300 SHINE 1275.748 1300 Pick-up side half-cell with beam pipe XFEL 1287.78 1300 TRIUMF 1287.78 1300 SHINE 1287.78 1300 Coupler side half-cell with beam pipe XFEL 1287.78 1300 TRIUMF 1288.136 1300 SHINE 1288.827 1300 2, deformed Middle half-cell XFEL 1275.603 1299.857 TRIUMF 1275.603 1299.857 SHINE 1275.603 1299.857 Pick-up side half-cell with beam pipe XFEL 1287.631 1299.855 TRIUMF 1287.631 1299.855 SHINE 1287.631 1299.855 Coupler side half-cell with beam pipe XFEL 1287.631 1299.855 TRIUMF 1287.977 1299.848 SHINE 1288.638 1299.865 4, deformed Middle half-cell XFEL 1275.449 1299.708 TRIUMF 1275.449 1299.708 SHINE 1275.449 1299.708 Pick-up side half-cell with beam pipe XFEL 1287.468 1299.695 TRIUMF 1287.468 1299.695 SHINE 1287.468 1299.695 Coupler side half-cell with beam pipe XFEL 1287.468 1299.695 TRIUMF 1287.817 1299.688 SHINE 1288.448 1299.733 6, deformed Middle half-cell XFEL 1275.299 1299.558 TRIUMF 1275.299 1299.558 SHINE 1275.299 1299.558 Pick-up side half-cell with beam pipe XFEL 1287.306 1299.534 TRIUMF 1287.306 1299.534 SHINE 1287.306 1299.534 Coupler side half-cell with beam pipe XFEL 1287.306 1299.534 TRIUMF 1287.656 1299.529 SHINE 1288.257 1299.600
下载: 导出CSV
表 7 不同调谐力对应的三种有加强筋1.3 GHz 9-cell射频腔场平坦度理论计算值与仿真计算值结果对比
Table 7. Results comparison of field flatness between theoretical and simulation calculations for XFEL, TRIUMF and SHINE candidate 1.3 GHz 9-cell SRF cavities with enhancement rings
Tuning force/kN (squeezed) F, (Field flatness) Theoretical calculation value Simulation calculation value 0, undeformed XFEL 100% 99.95% TRIUMF 100% 99.94% SHINE 100% 99.92% 2, deformed XFEL 99.84% 99.16% TRIUMF 99.27% 98.77% SHINE 97.35% 98.48% 4, deformed XFEL 99.54% 98.85% TRIUMF 99.17% 98.26% SHINE 95.48% 96.66% 6, deformed XFEL 99.14% 98.32% TRIUMF 98.85% 97.56% SHINE 93.44% 94.27%
下载: 导出CSV
-
[1] Aune B, Bandelmann R, Bloess D, et al. Superconducting TESLA cavities[J]. Physical Review Accelerators and Beams, 2000, 3: 092001. doi: 10.1103/PhysRevSTAB.3.092001 [2] Padamsee H, Knobloch J, Hays T. RF superconductivity for accelerators[M]. New York: Wiley, 1998. [3] Tajima T, Furuya T, Suzuki T. Pre-tuning of TRISTAN superconducting RF cavities[C]//Proceedings of the 4th Workshop on RF Superconductivity. 1989: 821-847. [4] Sekutowicz J, Chen Yinghua, Wei Yixiang. A different tuning method for accelerating cavities[C]//Proceedings of the 4th Workshop on RF Superconductivity. 1989: 849-857. [5] 朱航, 翟纪元, 戴建枰. 9-cell超导腔快速预调谐方法研究[J]. 强激光与粒子束, 2022, 34:104015Zhu Hang, Zhai Jiyuan, Dai Jianping. Research on fast pre-tuning method of 9-cell superconducting cavities[J]. High Power Laser and Particle Beams, 2022, 34: 104015 [6] Sun An, Wang Haipeng, Wu Genfa. Effect of the tuner on the field flatness of SNS superconducting RF cavities[C]//Proceedings of LINAC 2004. 2004: 815-817. [7] Sun An. Superconducting RF cavity frequency and field distribution sensitivity simulation[C]//Proceedings of 2005 Particle Accelerator Conference. 2005: 4194-4196. [8] 李波, 刘华昌, 王云, 等. CSNS-II超导椭球腔形变电场平坦度仿真分析[J]. 强激光与粒子束, 2021, 33:034001 doi: 10.11884/HPLPB202133.200259Li Bo, Liu Huachang, Wang Yun, et al. Simulating analysis on electric field flatness of deformed superconducting elliptical cavity for CSNS-II linac[J]. High Power Laser and Particle Beams, 2021, 33: 034001 doi: 10.11884/HPLPB202133.200259 [9] Posen S, Liepe M. Mechanical optimization of superconducting cavities in continuous wave operation[J]. Physical Review Accelerators and Beams, 2012, 15: 022002. doi: 10.1103/PhysRevSTAB.15.022002 [10] Zvyagintsev V, Beard C D, Grassellino A, et al. Nine-cell elliptical cavity development at TRIUMF[C]//Proceedings of SRF2011. 2011: 107-109. -
点击查看大图
计量
- 文章访问数: 577
- HTML全文浏览量: 203
- PDF下载量: 92
- 被引次数: 0
