Application development of RPT module based on OpenMC for double-heterogeneous system
-
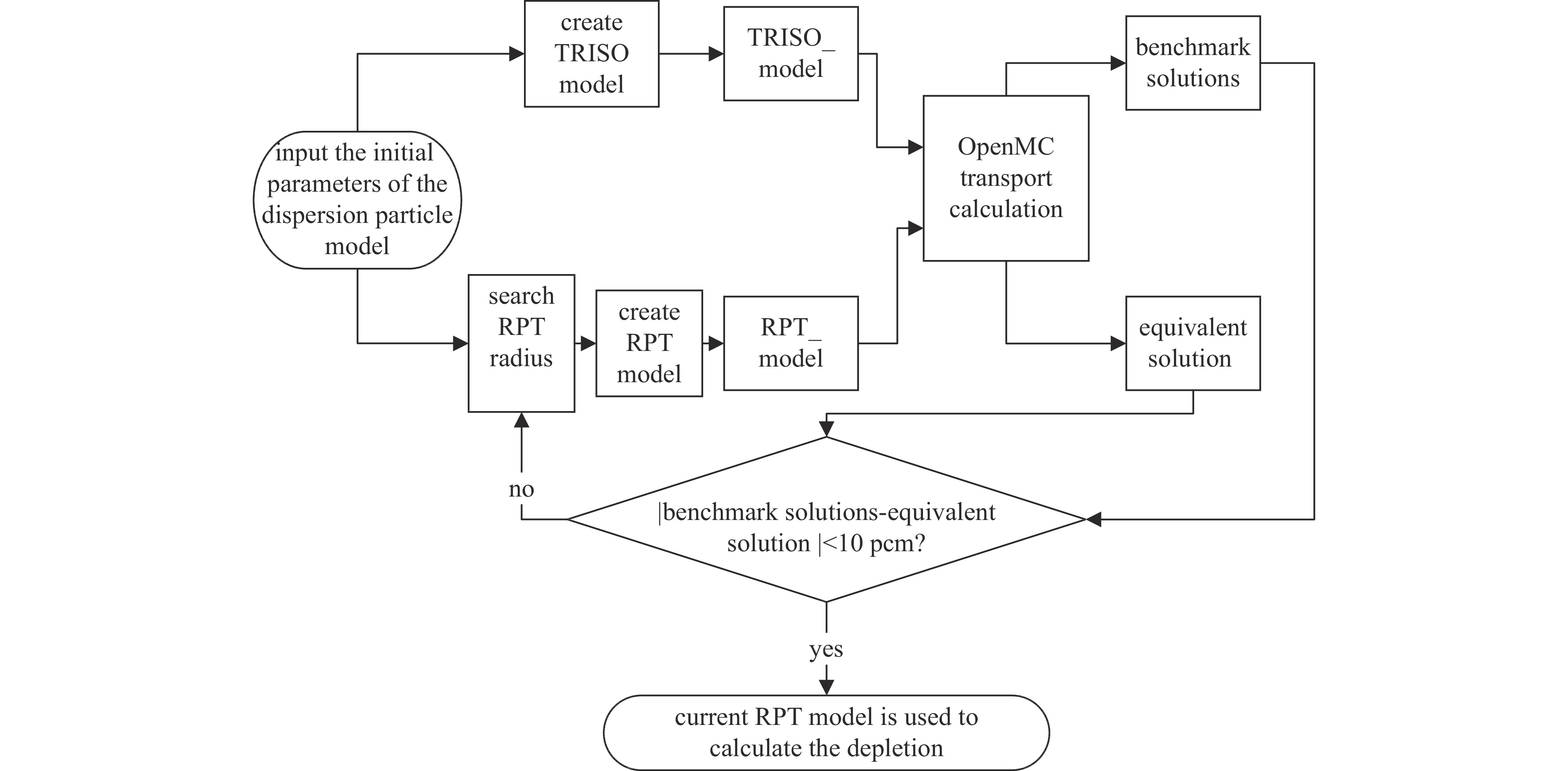
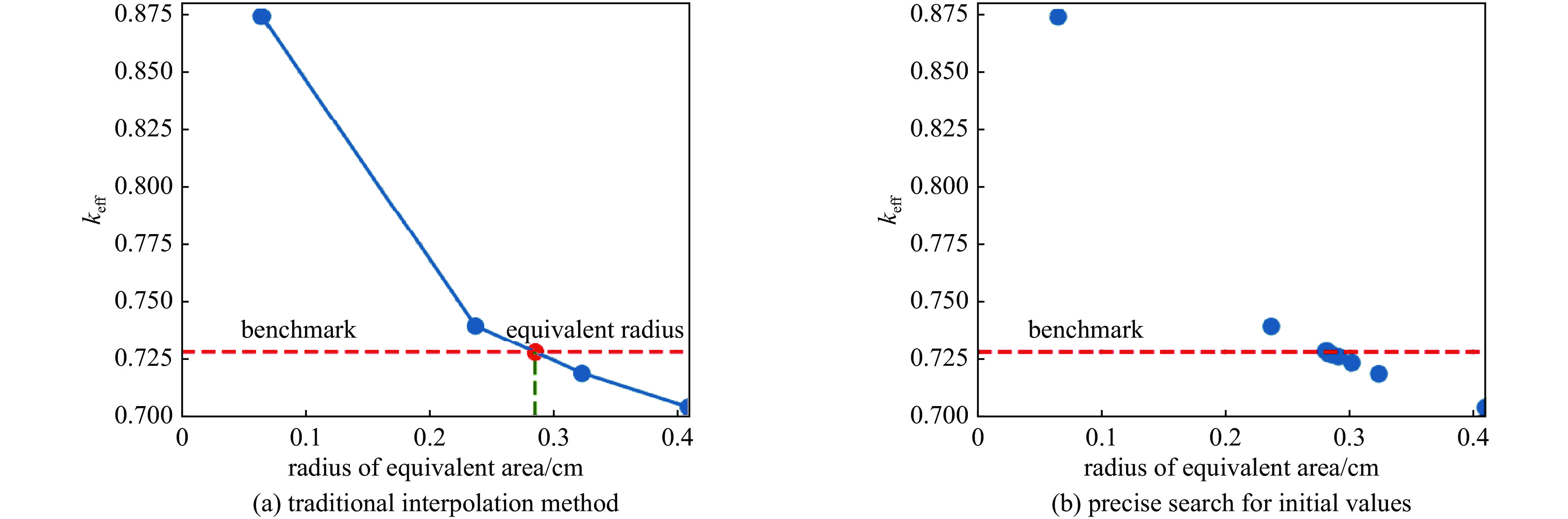
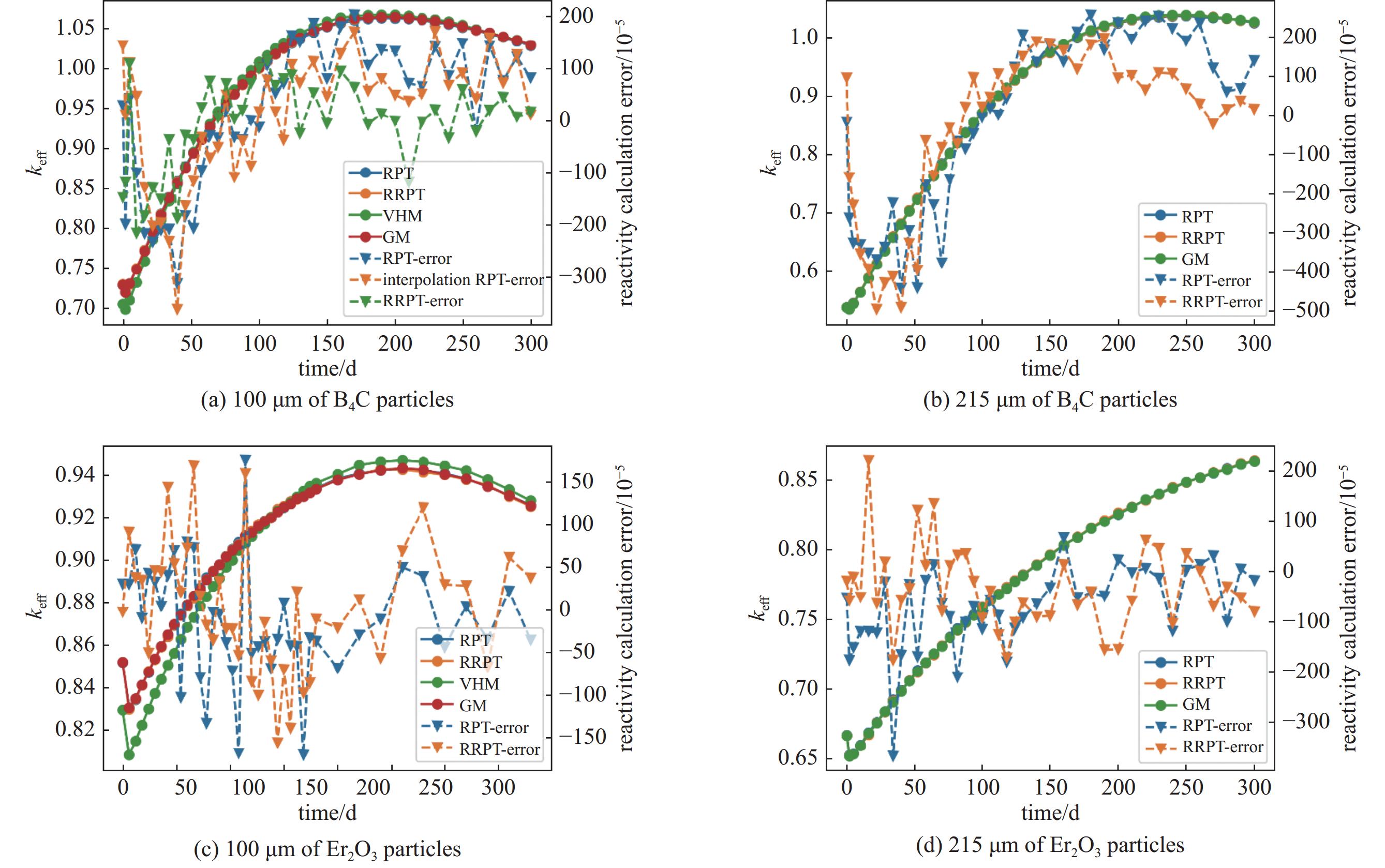
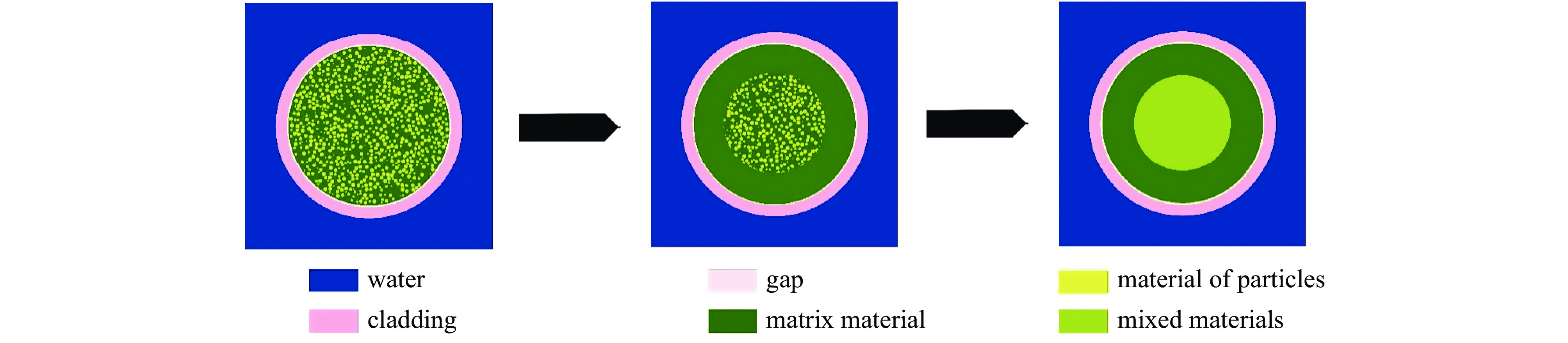
摘要: 由于基体中有着大量随机分布的弥散颗粒,双重非均匀系统具有复杂的几何结构,传统中子学计算方法往往难以处理双重非均匀系统,反应性等效物理转换(RPT)方法是常用的近似处理方法。通过分析RPT方法的三个关键步骤:精确初始值的求解、等效半径的求解、燃耗算法的选取,探讨了各步骤采用不同算法对RPT方法效率和精度的影响,并基于OpenMC在Python应用程序接口之上开发了RPT模块。数值结果表明,优化后的RPT模块,在保持良好计算效率的同时,也能满足工程计算精度的需要。
-
关键词:
- OpenMC /
- 双重非均匀系统 /
- 弥散颗粒燃料 /
- 反应性等效物理转换方法
Abstract: Due to the large number of randomly distributed dispersed particles in the matrix, the double heterogeneous (DH) system has a complex geometric structure, and it is often difficult to deal with the DH system using the traditional neutronics calculation method. The reactivity equivalent physical transformation (RPT) method is a commonly used approximation method. This paper analyzes the three key steps of the RPT method: the solution of the exact initial value, the solution of the equivalent radius, and the selection of the depletion algorithm. The influence of different algorithms on the efficiency and accuracy of the RPT method is discussed. Based on OpenMC, an RPT module is developed on the Python API. The numerical results show that the optimized RPT module can meet the needs of engineering calculation accuracy while maintaining good calculation efficiency. -
高功率微波(HPM)技术的不断发展[1-9]对高功率微波的功率、模式、频率等方面的测量要求越来越高。在HPM的测量技术中,HPM的在线测量是一种非常重要的测试方式和手段。HPM的在线测量不仅能够监测HPM系统的工作状态是否稳定,而且在良好标定的前提下也可以实现HPM的功率测量[10-17]。由于HPM一般在圆波导中传输,因此设置圆波导在线耦合器是常见的在线功率测量方法[18]。传统的耦合器往往只开有一个耦合孔,耦合孔内设置金属探针,将HPM功率耦合出一小部分后进行HPM功率的测量[19]。在HPM的在线测量中,除了要求对HPM功率进行测量之外,还对HPM系统内部混入的少量杂模的混合比也提出了测量的要求,而关于这方面的研究也仅限于模式的方向性测量[20],缺少确切的模式诊断方法。在实际的HPM系统中,一般使用的是圆波导TM01模式,但是由于种种原因,也往往混入了TE11模式。例如,在高功率微波系统中,为了提高功率和效率,微波系统往往采用过模波导,波导中可能激励出多种微波模式。再如,在虚阴极振荡器之类的高功率微波系统中,微波多模且模式不确定。此外在高功率微波的传输系统中,在一些不匹配连接处往往也会产生出其他干扰模式。但是这些干扰模式中,最有可能出现的是比TM01低的基模TE11模式,其他杂模如TE21和TE01等模式,仿真结果显示其含量非常小。因此,本文主要就TM01和TE11混模系统中如何提取 TE11模式信息的方法开展了研究。由于圆波导TM01模式在圆波导角向是旋转对称的,而TE11模式在角向是非对称的,因此TM01和TE11模式混合后,场分布在角向将出现非旋转对称的特点。所以,可以考虑在圆波导的角向设置多个耦合孔对TE11模式的信息进行提取。本文基于角向均匀分布的8孔耦合器进行了从TM01模式中提取TE11模式混合比和极化方向的分析和仿真研究,结果表明,采用8孔耦合器中相互正对的孔之间的平均功率,可以实现对TE11模式的混合比和极化角度进行提取,提取方法简单实用。
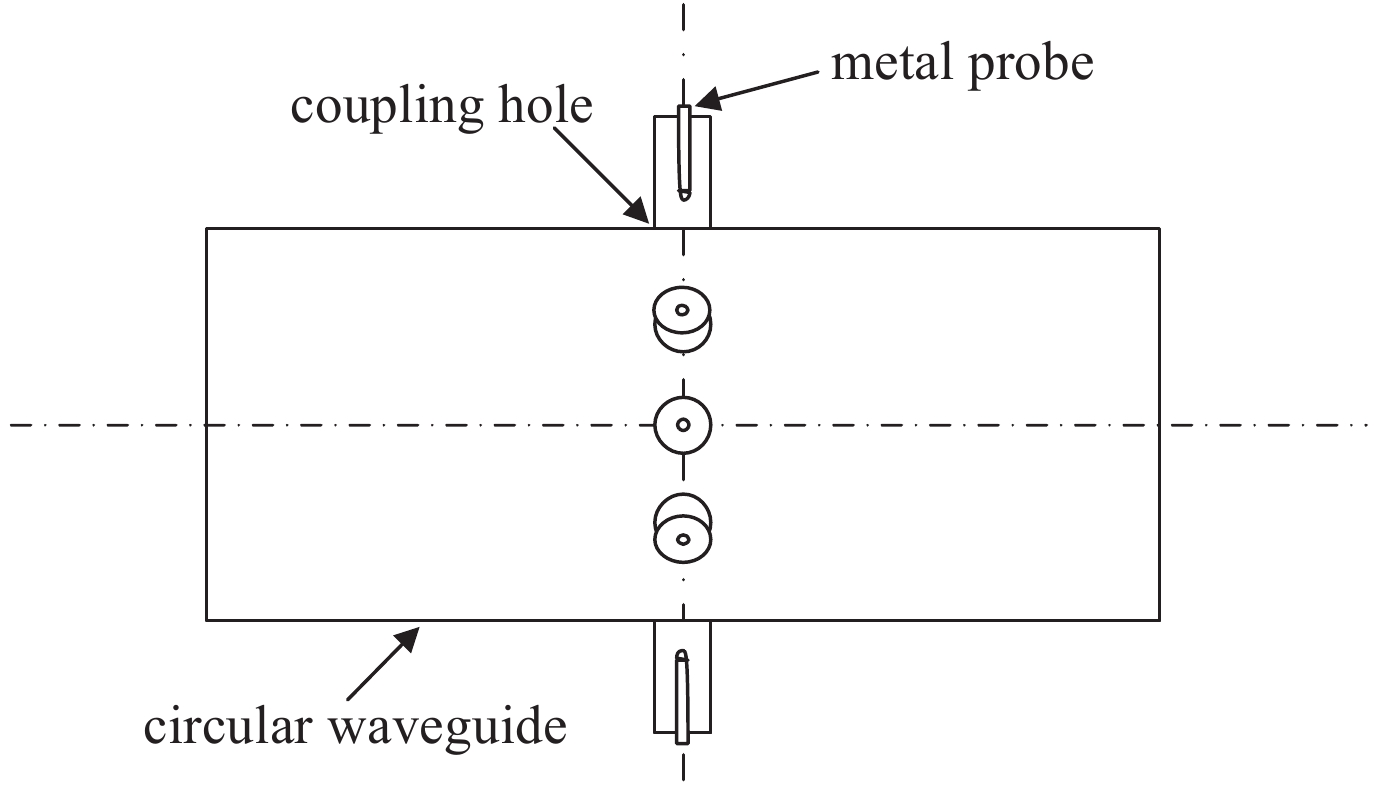
1. 圆波导八孔耦合器
1.1 圆波导八孔耦合器的结构
圆波导八孔耦合器采用电探针的耦合方式,于圆波导壁上,八个耦合孔沿圆波导的角向均匀分布,如图1所示。根据微波频率,耦合器被设计成只能传输TM01及以下的低次模。相比传统的单孔耦合器和三孔耦合器,八孔耦合器可以利用对向端口的平均功率对波导的传输模式进行分析和诊断。
1.2 圆波导中TM01模式和TE11模式
图2给出了TM01模式和TE11模式的场分布示意图,TM01模式的电场在圆波导角向均匀分布,而TE11模式的电场在圆波导中沿某种极化方向呈对称分布,因此当TM01模式混合入TE11模式时,圆波导内壁的电场强度将从均匀分布逐渐变为沿TE11极化方向对称的不均匀分布。通过对这种不均匀性变化规律进行模拟分析,可为模式混合的诊断提供指导。
2. 提取TE11模式信息的原理
2.1 混合模式在耦合孔处的电场分析
由文献[10]可知,经电探针耦合出来的功率与耦合孔处的径向电场相关。因此,在圆波导壁的耦合孔处,设ETM01、ETE11分别为TM01和TE11模式的径向电场幅度,φ1、φ2分别为TM01和TE11模式的相位,则TM01和TE11模式在耦合孔处的径向电场E01、E02分别为
{E01=ETM01sinφ1E02=ETE11sinφ2 (1) 混合模式在该处的径向电场
E=E01+E02=ETM01sinφ1+ETE11sinφ2 (2) 混合模式的径向电场也可以表示为模式幅度和相位的正弦函数,即
E=E0sin(ETM01,φ1,ETE11,φ2) (3) 其中,混合电场的幅度
E20=ETM012+ETE112+2ETM01ETE11cos(φ1−φ2) (4) 两个模式的相位差Δφ=φ1−φ2,为
tan(Δφ)=ETM01sinφ1+ETE11sinφ2ETM01cosφ1+ETE11cosφ2 (5) 考虑耦合度后,从各耦合孔检测出的功率Pi(i=1,2,…,8)为
Pi=C2TM01ETM012+C2TE11,iETE11,i2+2CTM01CTE11,iETM01ETE11,icos(Δφ) (6) 式中:C代表相应模式的耦合度。对于TM01模式,8个孔的耦合度相等,但是对于TE11模式,8个孔的耦合度是有差别的,与TE11模式的极化角度有关。
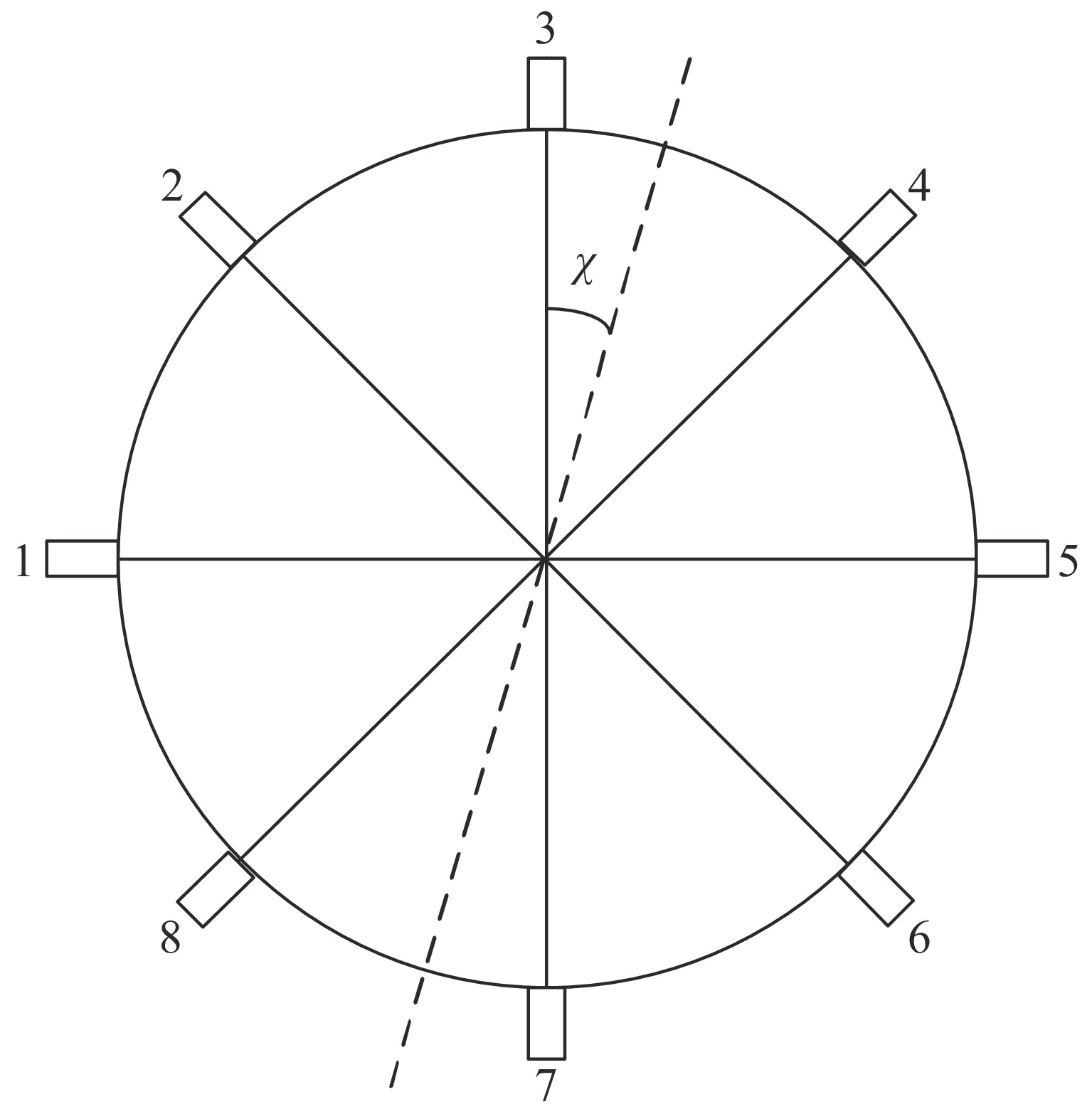
图3为耦合孔端口编号的示意图。由图2所示的TM01和TE11模式的电场分布,并结合图3的端口序号,不难看出,下列关系是成立的
{ETE11,1=−ETE11,5ETE11,2=−ETE11,6ETE11,3=−ETE11,7ETE11,4=−ETE11,8 (7) {CTE11,1=CTE11,5CTE11,2=CTE11,6CTE11,3=CTE11,7CTE11,4=CTE11,8 (8) 将式(7)和式(8)代入式(6)后,得到8个孔的平均功率
ˉP 以及相互正对孔的平均功率,即,3、7号孔的平均功率ˉP3,7 ,2、6号孔的平均功率ˉP2,6 ,4、8号孔的平均功率ˉP4,8 以及1、5号孔的平均功率ˉP1,5 分别为ˉP=C2TM01E2TM01+C2TE11,1E2TE11,1+C2TE11,2E2TE11,2+C2TE11,3E2TE11,3+C2TE11,4E2TE11,48+C2TE11,5E2TE11,5+C2TE11,6E2TE11,6+C2TE11,7E2TE11,7+C2TE11,8E2TE11,88=C2TM01E2TM01+C2TE11,1E2TE11,1+C2TE11,2E2TE11,2+C2TE11,3E2TE11,3+C2TE11,4E2TE11,44 (9) {ˉP1,5=C2TM01E2TM01+C2TE11,1E2TE11,12+C2TE11,5E2TE11,52ˉP2,6=C2TM01E2TM01+C2TE11,2E2TE11,22+C2TE11,6E2TE11,62ˉP3,7=C2TM01E2TM01+C2TE11,3E2TE11,32+C2TE11,7E2TE11,72ˉP4,8=C2TM01E2TM01+C2TE11,4E2TE11,42+C2TE11,8E2TE11,82 (10) 结果表明,上述各平均功率只是与圆波导中通过的总功率、各模式的比例以及TE11模式在各端口的耦合度有关,而与相位差无关,这对实际测量TE11模式的混合比和极化角度提供了极大的方便,这就是用8孔耦合器的原因。
2.2 提取TE11模式信息的思路
如图3所示,若TE11模式极化方向为3号端口和7号端口的连线方向,即χ=0(°)的情况,那么可以定性分析得出,随着TE11模式混合比的增加,此时3、7端口的耦合度增加,而1、5端口的耦合度减小,因此
ˉP3,7 随之增加而ˉP1,5 减小。同时,由于端口的对称性,2、6号端口的耦合度与4、8端口的耦合度均相等,因此ˉP2,6=ˉP4,8 。随着TE11模式混合比的增加,ˉP3,7−ˉP1,5 逐渐增大,但始终有ˉP2,6=ˉP4,8 成立。这说明,ˉP3,7−ˉP1,5 是提取TE11模式混合比的关键。然而,在实际的微波系统中,TE11模式的极化方向通常是随机的,而极化方向又影响了各耦合孔的耦合度,因此TE11模式的极化方向对8个端口测得的功率都有影响。假定TE11模式极化方向与3端口和7端口的连线方向成χ夹角,如图3所示,此时必然
ˉP2,6−ˉP4,8≠0 ,且当TE11的极化角度增加时,ˉP2,6 与ˉP4,8 的差别越来越大。这种非对称性为判断TE11极化方向奠定了基础。另外,为了消除圆波导中总功率对各端口功率的影响,研究功率比
(ˉP2,6−ˉP4,8)/ˉP 、(ˉP3,7−ˉP1,5)/ˉP 与TE11模式混合比以及极化角度的关系,是实现对TE11模式信息提取的合理思路。3. 提取TE11模式信息的仿真研究
选取频率为9.7 GHz,采用CST仿真了8个端口的功率与TE11模式混合比和极化角度的关系。由于8个端口角向间隔为45°,因此只需要考虑χ在0°~22.5°范围内的情况即可。仿真时,圆波导中设置激励为TM01模式与TE11模式混合输入,由截止波导内的电探针采集耦合信号,即可得到各端口的功率。
3.1 相位差对端口输出功率比的影响
在圆波导中输入总功率为1 GW、TE11模式的功率为0.3 GW,即混合比ρ=30%,以及TE11模式的极化角度χ=12.5°的情况下,我们仿真了两模式之间的相位差从0~360˚变化时,8个端口的功率变化情况,并计算了相互正对端口的平均功率与8个端口平均功率的比。结果如表1所示,
ˉP1,5/ˉP 、ˉP2,6/ˉP 、ˉP3,7/ˉP 、ˉP4,8/ˉP 与相位差无关,验证了2.1的分析。表 1 功率比与相位差的关系Table 1. Relationship between power ratio and phase differenceΔφ/(°) ˉP3,7/ˉP ˉP2,6/ˉP ˉP4,8/ˉP ˉP1,5/ˉP 0 1.165 0.923 1.076 0.834 70 1.165 0.923 1.076 0.834 140 1.165 0.923 1.076 0.834 210 1.165 0.924 1.076 0.834 280 1.165 0.923 1.076 0.834 350 1.165 0.923 1.076 0.834 3.2 TE11模式的混合比和极化角度对端口输出功率比的影响
固定圆波导的输入总功率,并设两个模式的相位差为0˚,模拟了TE11模式的极化角度χ为0~22.5˚时且模式混合比ρ为0~10%时,8个端口的功率变化规律。
仿真结果显示,当圆波导中传输的为纯TM01模式时,8个端口功率基本一致。当传输的微波中混有TE11模式时,端口3与端口7功率发生明显变化,且这种变化随着TE11模式混合比增加而增大。当存在TE11模式时,端口2和端口4的功率以及端口6和端口8的功率从对称变化成非对称,且当TE11模式的极化角度增加时,这种非对称现象表现的越明显。
研究发现,
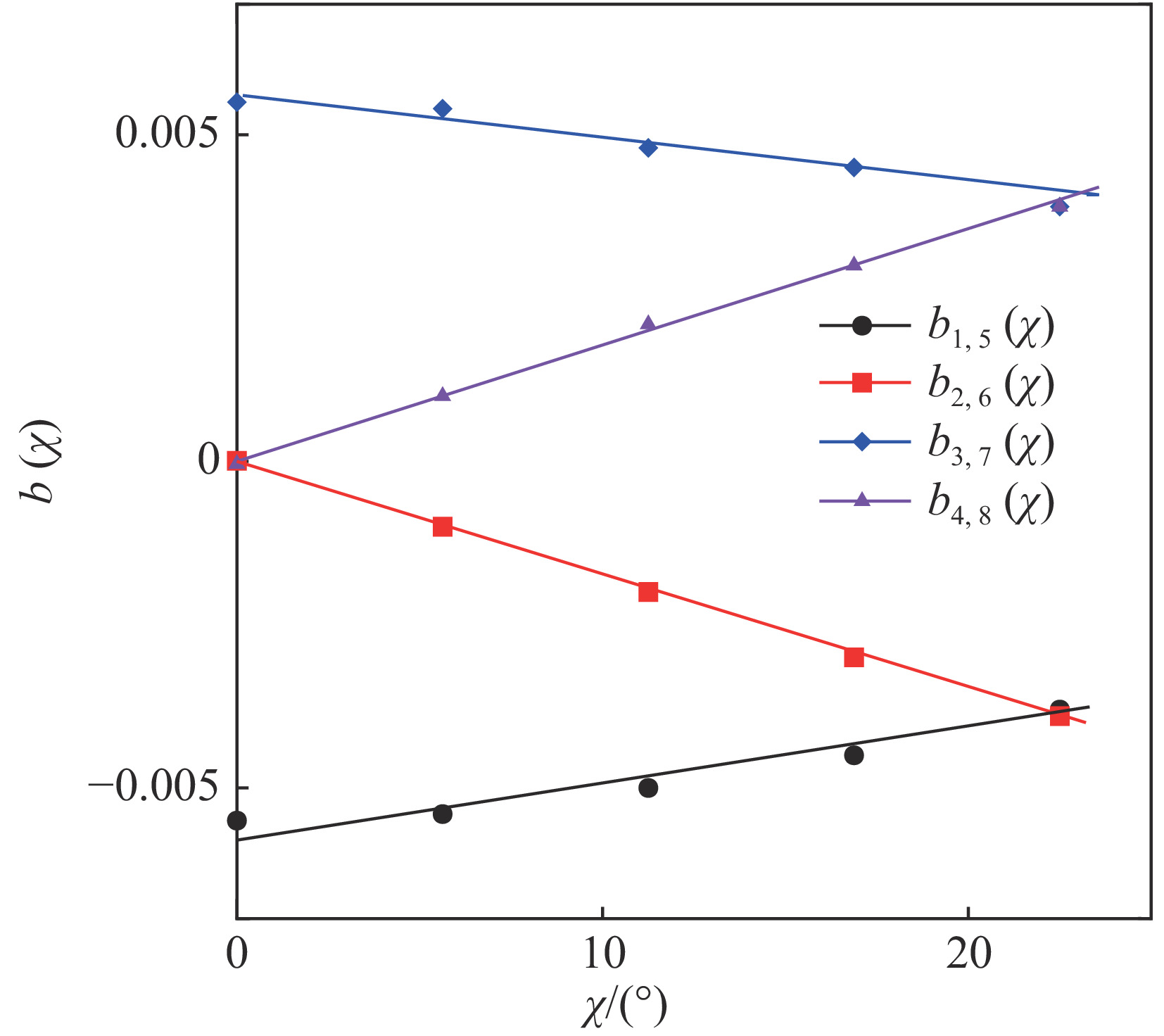
ˉP1,5/ˉP 、ˉP2,6/ˉP 、ˉP3,7/ˉP 、ˉP4,8/ˉP 都与TE11模式的极化角度χ和模式混合比ρ有关,如表2所示。由表2可以看出,在给定的混合比范围内,各功率比均可以用式(11)所示的线性关系表示,其中系数b与极化角度χ有关。表 2 功率比与极化角度和模式混合比的关系Table 2. Relationship between power ratio and polarization angle and mode mixing ratioχ/(°) ρ/% ˉP1,5/ˉP ˉP2,6/ˉP ˉP3,7/ˉP ˉP4,8/ˉP 0 0 0.999 0.999 1.000 1.000 2 0.989 1.000 1.010 1.000 4 0.978 1.000 1.021 1.000 6 0.968 0.998 1.032 1.000 8 0.956 1.000 1.043 0.999 10 0.945 1.000 1.054 0.9991 5.625 0 0.999 0.999 1.000 1.000 2 0.989 0.997 1.010 1.002 4 0.979 0.995 1.020 1.004 6 0.968 0.993 1.031 1.006 8 0.957 0.991 1.042 1.008 10 0.946 0.989 1.053 1.010 11.25 0 0.999 0.999 1.000 1.000 2 0.988 0.993 1.015 1.002 4 0.980 0.991 1.019 1.008 6 0.970 0.987 1.029 1.012 8 0.960 0.983 1.040 1.016 10 0.949 0.979 1.050 1.020 16.875 0 0.999 0.999 1.000 1.000 2 0.991 0.994 1.008 1.006 4 0.982 0.988 1.017 1.011 6 0.973 0.982 1.026 1.017 8 0.964 0.975 1.035 1.024 10 0.954 0.969 1.045 1.030 22.5 0 0.999 0.999 1.000 1.000 2 0.992 0.992 1.007 1.007 4 0.985 0.985 1.015 1.014 6 0.977 0.977 1.022 1.022 8 0.969 0.969 1.030 1.031 10 0.961 0.961 1.038 1.038 {ˉP4,8ˉP=b4,8(χ)⋅ρ+1ˉP2,6ˉP=b2,6(χ)⋅ρ+1ˉP3,7ˉP=b3,7(χ)⋅ρ+1ˉP1,5ˉP=b1,5(χ)⋅ρ+1 (11) 对表2数据进行分析后,发现b与极化角度
χ 基本上符合线性关系,如图4所示。因此,根据式(11)可以得到经过数据拟合后的公式为
{ˉP2,6−ˉP4,8ˉP=(−0.0004χ−0.00007)⋅ρˉP3,7−ˉP1,5ˉP=(−0.0001χ+0.0113)⋅ρ (12) 由此得到计算TE11模式极化角度和混合比的表达式为
{χ=−0.00007ˉP3,7−ˉP1,5ˉP−0.0113ˉP2,6−ˉP4,8ˉP−0.0001ˉP2,6−ˉP4,8ˉP+0.0004ˉP3,7−ˉP1,5ˉPρ=ˉP3,7−ˉP1,5ˉP−0.0001χ+0.0113 (13) 式(13)表明,在实际测量中,只要我们通过8孔耦合器测量出各孔的输出功率,就可以按照式(13)计算出TE11模式的相关信息。
3.3 式(13)可行性的验证
为了验证式(13)的可行性,设置不同的相位差、TE11模式混合比和极化角度,采用CST计算出各端口的输出功率,然后按照式(13)计算出TE11模式的相关信息,并与设定值进行比较,结果如表3所示,其中ρs和χs为仿真中的设定值,ρc和χc为按照式(13)计算所得结果。
表 3 计算结果与设定值的比较Table 3. Comparison of calculation result and set valueΔφ/(°) ρs/% χs/(°) ρc/% χc/(°) Δρ/% Δχ/% values of parameters in simulation calculation results by formula-13 error 0 3 12.5 2.819 11.764 6.033 5.888 70 3 12.5 2.810 11.800 6.333 5.600 140 3 12.5 2.817 11.689 6.100 6.488 210 3 12.5 2.817 11.689 6.100 6.488 280 3 12.5 2.808 11.724 6.400 6.208 350 3 12.5 2.819 11.764 6.033 5.888 0 5 12.5 4.760 11.640 4.800 6.880 70 5 12.5 4.754 11.706 4.920 6.352 140 5 12.5 4.768 11.619 4.640 7.048 210 5 12.5 4.749 11.616 5.020 7.072 280 5 12.5 4.749 11.616 5.020 7.072 350 5 12.5 4.770 11.664 4.600 6.688 0 7 12.5 6.741 11.619 3.700 7.048 70 7 12.5 6.749 11.604 3.585 7.168 140 7 12.5 6.731 11.602 3.842 7.184 210 7 12.5 6.726 11.537 3.914 7.704 280 7 12.5 6.737 11.555 3.757 7.560 350 7 12.5 6.749 11.604 3.585 7.168 0 3 0 2.795 −0.259 6.833 70 3 0 2.802 −0.344 6.600 140 3 0 2.794 −0.344 6.866 210 3 0 2.777 −0.345 7.433 280 3 0 2.787 −0.260 7.100 350 3 0 2.806 −0.175 6.466 0 5 0 4.717 −0.225 5.660 70 5 0 4.726 −0.225 5.480 140 5 0 4.713 −0.327 5.740 210 5 0 4.711 −0.378 5.780 280 5 0 4.713 −0.327 5.740 350 5 0 4.715 −0.276 5.700 0 7 0 6.681 −0.283 4.557 70 7 0 6.669 −0.356 4.728 140 7 0 6.669 −0.356 4.728 210 7 0 6.665 −0.428 4.785 280 7 0 6.669 −0.356 4.728 350 7 0 6.685 −0.355 4.500 从表3的验算结果可以看出,用式(13)计算出的TE11模式混合比和极化角度与仿真设定的基本吻合,误差均小于10%,说明用式(13)计算TE11模式的相关信息是可行的。
4. 讨 论
4.1 式(13)的应用范围
在相位差为0的情况下,我们随机选取了对应于表4中的极化角度,在此情况下,仿真了不同混合比时,用式(13)计算出的TE11模式混合比和极化角度的相对误差。可以看出,极化角度的误差均在10%以内。当设定的混合比超过30%时,混合比的误差明显增大,并超过10%。由于实际使用中要求误差不超过10%,因此式(13)的应用范围在 0~30%之间。事实上,当 TE11 模式的混合比超过 30%之后,式(11)中的 b 与极化角度 χ 偏离线性关系,是造成误差增加的主要原因。此时,若将 b与极化角度 χ以复杂的非线性关系进行拟合的话,本文方法仍将适合于混合比超过 30%的情况。但是实际使用过程中,通过以往辐射场测量的结果显示,TE11 模式的混合比不会超过 5%,因此本文主要考虑混合比为0~10%的情况,故采用了最简单的线性拟合,以方便实际应用。
表 4 式(13)的应用范围Table 4. Application range of formula (13)ρs/% χs/(°) ρc/% χc/(°) Δρ/% Δχ/% values of parameters in simulation calculation results by formula-13 error 2 5.625 1.911 5.378 4.450 −2.343 3 12.500 2.819 11.764 6.033 5.888 4 5.625 3.851 5.143 3.725 4.005 5 12.500 4.760 11.640 4.800 6.880 6 11.250 5.795 10.407 3.416 7.493 7 12.500 6.741 11.619 3.700 7.048 8 5.625 7.895 5.085 1.312 9.600 10 16.875 9.371 16.052 6.290 4.877 30 12.500 32.653 11.510 −8.843 7.920 50 12.500 61.130 11.518 −22.26 7.856 70 12.500 97.920 11.490 −39.885 8.080 4.2 TE11模式相关信息的具体判断方法
在实际HPM情况下使用时,应避免在耦合器中通过过高的微波功率,以免造成耦合器损坏或工作不稳定。因此,选取合适的耦合孔处的倒角半径和加工光滑程度,继而提升耦合器的功率容量是非常必要的。在满足功率容量的情况下,以及在对耦合器输出功率精确测量的前提下,具体判断TE11模式的信息方法如下。
首先,用纯TM01模式的激励器,对耦合器进行耦合度的标定,也就是调整探针的位置,对耦合器的各个端口的耦合度进行调整,使其一致。
其次,在TM01和TE11混合模式下,测量各端口的输出功率。
第三,观察图1中各端口的输出功率数据是否对称,判断传输微波中是否含有TE11模式,若不对称,且最大值和最小值的连线在耦合器的某一直径线上,说明有TE11模式。
第四,依据输出功率最大值与最小值对应的端口,标出对应的3端口和7端口,并按照图3标出相应的其它端口编号。
第五,利用端口2与端口4,端口6与端口8功率的非对称性,判断出极化角度落在端口3与端口7连线的某一侧。若
(ˉP2,6−ˉP4,8)/ˉP<0 ,则表示落在端口3与4之间,即图3所示的那样,反之,落在3与2之间。最后,采用用式(13),计算出TE11模式的混合比ρ和具体的极化角度χ。
5. 结 论
针对HPM系统中,圆波导中传输的TM01与TE11混合模式的实际情况,本文采用角向均匀分布的8孔耦合器,对TE11模式的混合比和极化角度等信息进行了提取方法的研究。
通过对圆波导中TM01模式和TE11模式在耦合器耦合孔处电场的分析,得出相互正对耦合孔之间的平均功率与8个孔的平均功率之比
ˉP1,5/ˉP 、ˉP2,6/ˉP 、ˉP3,7/ˉP 、ˉP4,8/ˉP 与模式之间的相位差无关,并通过CST仿真得到了验证。分析还表明,为了消除圆波导中总功率对各端口功率的影响,以功率比(ˉP2,6−ˉP4,8)/ˉP 、(ˉP3,7−ˉP1,5)/ˉP 为研究目标,更加有利于实际场合中用8孔耦合器进行TE11模式混合比和极化角度的提取,使提取方法简单实用。CST仿真结果还表明,在TE11模式的混合比小于30%的情况下,功率比
(ˉP2,6−ˉP4,8)/ˉP 、(ˉP3,7−ˉP1,5)/ˉP 正比于TE11模式的混合比ρ,比例系数b是极化角度χ的线性函数。进而给出了计算TE11模式混合比和极化方向的表达式(13)。反演结果验证了式(13)是可行的,在TE11模式混合比小于30%时,用它计算TE11模式的混合比和极化角度误差均不超过10%。
在此基础上,本文给出了实际情况下TE11模式相关信息的具体判断方法。
-
表 1 棒状几何燃料栅元主要参数
Table 1. Main parameters of fuel pin
pitch/cm radius
of fuel
region/cmthickness
of air
gas/cmmaterial
of
matrixmatrix
enrichment
ratio/%density of
matrix/
(g·cm−3)material
of
cladding/cmthickness of
zirconium
cladding/cmdensity of
zirconium cladding/
(g·cm−3)density of
moderate H2O/
(g·cm−3)temperature/K 1.26 0.4096 0.0084 UO2 20 10.5 Zr 0.057 6.5 1.0 300 表 2 随机弥散毒物颗粒模型参数
Table 2. Parameters of dispersed poison particles
material of particles radius of particles/μm volumetric fraction of particles/% density of fuel particles/(g·cm−3) B4C 100/215 5 1.9 Er2O3 100/215 5 8.6 表 3 不同晶格划分方法对弥散颗粒系统计算的影响
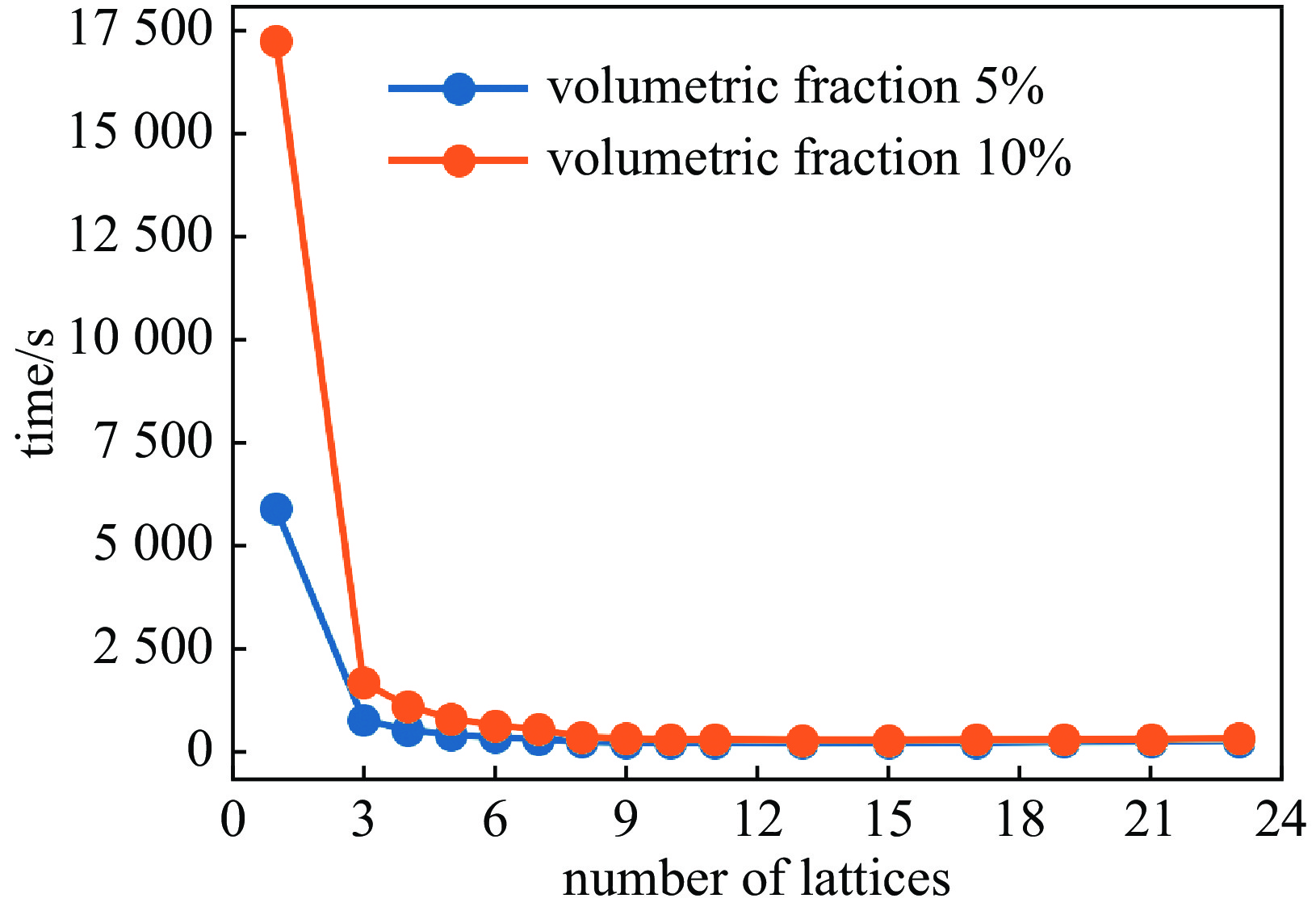
Table 3. Effects of different lattice partition methods on the calculation of dispersed particle system
lattice division
methodcomputing time/s Kinf volumetric fraction 5% volumetric fraction 10% volumetric fraction 5% volumetric fraction 10% 1×1×1(no lattice) 5868.359 17236.021 1.45644 1.61679 3×3×3 732.663 1639.056 1.45538 1.61731 5×5×5 376.934 769.323 1.45602 1.61757 7×7×7 270.646 503.730 1.45558 1.61638 10×10×10 177.279 262.550 1.45651 1.61755 13×13×13 174.607 247.808 1.45698 1.61752 15×15×15 177.633 246.969 1.45634 1.61741 17×17×17 182.233 254.476 1.45673 1.61613 19×19×19 200.549 260.858 1.45546 1.61734 21×21×21 206.945 271.748 1.45615 1.61748 表 4 OpenMC生成颗粒时间
Table 4. Particle generation time of OpenMC
volumetric
fraction/%particle
numberconsumption
time/s5 5033 0.67583202 10 10066 1.49383474 20 20132 3.50719374 30 30198 17.73238749 40 40265 156.2571 -
[1] 娄磊, 柴晓明, 姚栋, 等. 弥散颗粒系统双重非均匀性物理边界研究[J]. 核动力工程, 2021, 42(s2):82-88 doi: 10.13832/j.jnpe.2021.S2.0082Lou Lei, Chai Xiaoming, Yao Dong, et al. Research of double-heterogeneity physical boundary on dispersed particle-type systems[J]. Nuclear Power Engineering, 2021, 42(s2): 82-88 doi: 10.13832/j.jnpe.2021.S2.0082 [2] Brown F B, Martin W R. Stochastic geometry capability in MCNP5 for the analysis of particle fuel[J]. Annals of Nuclear Energy, 2004, 31(17): 2039-2047. doi: 10.1016/j.anucene.2004.08.006 [3] 刘仕倡, 王 侃, 陈义学. 改进弦长抽样方法开发及在弥散燃料蒙特卡罗模拟的应用[J]. 原子能科学技术, 2020(9):54Liu Shichang, Wang Kan, Chen Yixue. Development of Improved chord-length sampling method and its application in Monte Carlo simulation of dispersion fuel[J]. Atomic Energy Science and Technology, 2020(9): 54 [4] Murata I, Takahashi A, Mori T, et al. New sampling method in continuous energy Monte Carlo calculation for pebble bed reactors[J]. Journal of Nuclear Science and Technology, 1997, 34(8): 734-744. doi: 10.1080/18811248.1997.9733737 [5] Ji Wei, Martin W R. Monte Carlo simulation of VHTR particle fuel with chord length sampling[C]//Proceedings of 2007 Joint International Topical Meeting on Mathematics & Computation and Supercomputing in Nuclear Applications. 2007: 42104-48109. [6] Liang C. Radiation transport computation in stochastic media: method and application[D]. Troy: Rensselaer Polytechnic Institute, 2014. [7] She Ding, Liu Zhihong, Shi Lei. An equivalent homogenization method for treating the stochastic media[J]. Nuclear Science and Engineering, 2017, 185(2): 351-360. doi: 10.1080/00295639.2016.1272363 [8] Hebért A. A collision probability analysis of the Double-Heterogeneity problem[J]. Nuclear Science and Engineering, 1993, 115(2): 177-184. doi: 10.13182/NSE115-177 [9] Sanchez R, Pomraning G C. A statistical analysis of the double heterogeneity problem[J]. Annals of Nuclear Energy, 1991, 18(7): 371-395. doi: 10.1016/0306-4549(91)90073-7 [10] 朱彤, 陈玉清, 李昂, 等. 基于SuperMC的随机介质程序在双重非均匀性问题中的应用[J]. 强激光与粒子束, 2022, 34:026013 doi: 10.11884/HPLPB202234.210301Zhu Tong, Chen Yuqing, Li Ang, et al. Application of random media program based on SuperMC in solving double-heterogeneity[J]. High Power Laser and Particle Beams, 2022, 34: 026013 doi: 10.11884/HPLPB202234.210301 [11] Kim Y, Kim K S, Noh J M. Reactivity-equivalent physical transformation for homogenization of double-heterogeneous fuels[C]//Transactions of the Korean Nuclear Society Autumn Meeting. 2005. [12] Romano P K, Horelik N E, Herman B R, et al. OpenMC: a state-of-the-art Monte Carlo code for research and development[J]. Annals of Nuclear Energy, 2015, 82: 90-97. doi: 10.1016/j.anucene.2014.07.048 [13] Li Jian, She Ding, Shi Lei. An improved reactivity-equivalent physical transformation for treating FCM fuel with burnable poisons[J]. Annals of Nuclear Energy, 2018, 121: 577-581. doi: 10.1016/j.anucene.2018.08.024 [14] Lou Lei, Peng Xingjie, Chai Xiaoming, et al. The ring RPT method for DH systems containing dispersed particle-type of fuel and burnable poisons[J]. Frontiers in Energy Research, 2021, 9: 704307. doi: 10.3389/fenrg.2021.704307 [15] Lou Lei, Yao Dong, Chai Xiaoming, et al. A novel reactivity-equivalent physical transformation method for homogenization of double-heterogeneous systems[J]. Annals of Nuclear Energy, 2020, 142: 107396. doi: 10.1016/j.anucene.2020.107396 [16] Lou Lei, Chai Xiaoming, Yao Dong, et al. Research of ring RPT method on spherical and cylindrical Double-Heterogeneous systems[J]. Annals of Nuclear Energy, 2020, 147: 107741. doi: 10.1016/j.anucene.2020.107741 [17] Torquato S, Uche O U, Stillinger F H. Random sequential addition of hard spheres in high Euclidean dimensions[J]. Physical Review E, 2006, 74: 061308. doi: 10.1103/PhysRevE.74.061308 [18] Yu Jiankai, Forget B. Verification of depletion capability of OpenMC using VERA depletion benchmark[J]. Annals of Nuclear Energy, 2022, 170: 108973. doi: 10.1016/j.anucene.2022.108973 期刊类型引用(3)
1. 陈家辉,周振宇,翁明,曹猛. 圆波导TM_(01)模式转换器中TE_(11)和TE_(21)模式对圆波导耦合器耦合度的影响. 真空科学与技术学报. 2024(06): 492-502 .  百度学术
百度学术2. 雷乐,周振宇,翁明,林舒,曹猛. S波段矩形波导TE_(10)-圆波导TM_(01)模式转换器的研究. 真空科学与技术学报. 2023(06): 537-546 .  百度学术
百度学术3. 周振宇,陈家辉,翁明,林舒,曹猛. 同轴横电磁波转圆波导横磁波01模式的转换器研究. 西安交通大学学报. 2023(11): 171-180+205 .  百度学术
百度学术其他类型引用(0)
-






 下载:
下载:

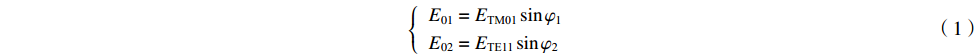
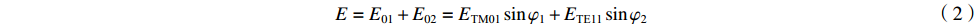

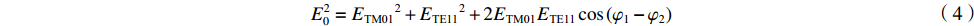
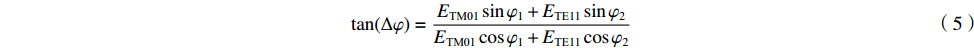



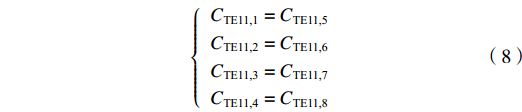
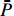
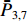
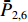
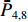
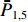
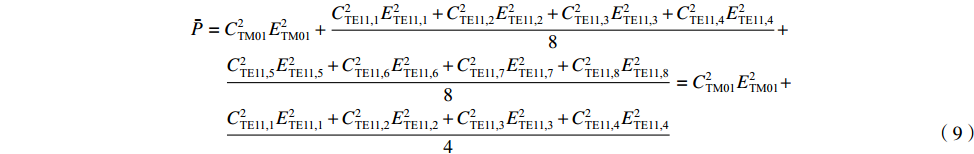
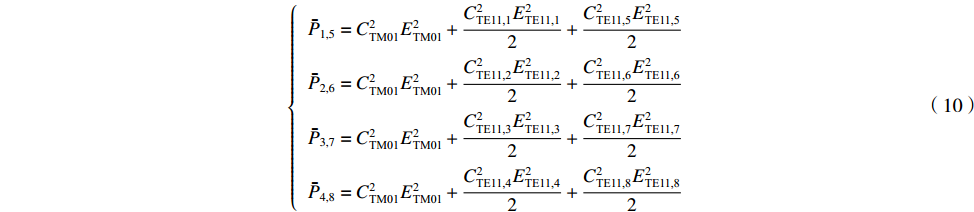
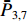
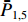
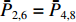
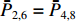
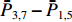
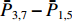
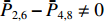
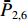
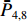
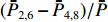
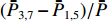
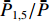
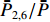
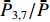
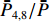
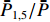
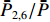
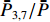
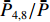
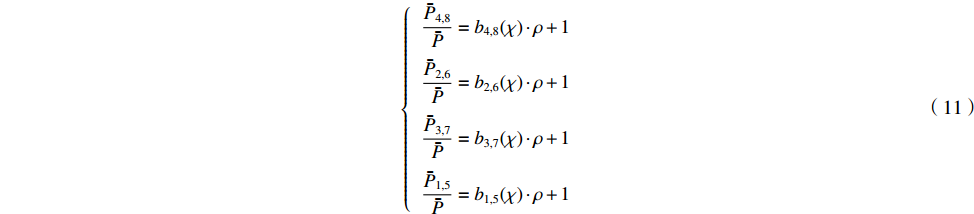


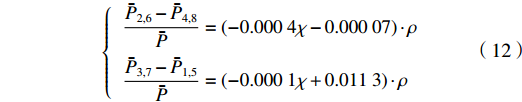
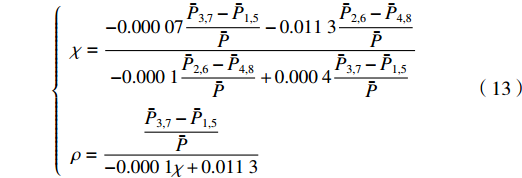
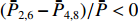
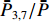
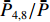
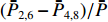
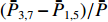
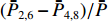
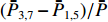
 下载:
下载: