基于高能逃逸电子机制的气体开关自击穿稳定性

耿玖源; 崔言程; 王海涛; 朱丹妮

doi:10.11884/HPLPB202436.240305

基于高能逃逸电子机制的气体开关自击穿稳定性

doi: 10.11884/HPLPB202436.240305

海军工程大学军用电气科学与技术研究所，武汉 430000

基金项目: 国家自然科学基金项目(62301585)

详细信息

作者简介:
耿玖源，gengjiuyuan@foxmail.com

中图分类号: TL503
计量
- 文章访问数: 227
- HTML全文浏览量: 65
- PDF下载量: 30
- 被引次数: 6
出版历程
- 收稿日期: 2024-09-04
- 修回日期: 2024-10-11
- 录用日期: 2024-10-14
- 网络出版日期: 2024-10-15
- 刊出日期: 2024-11-01

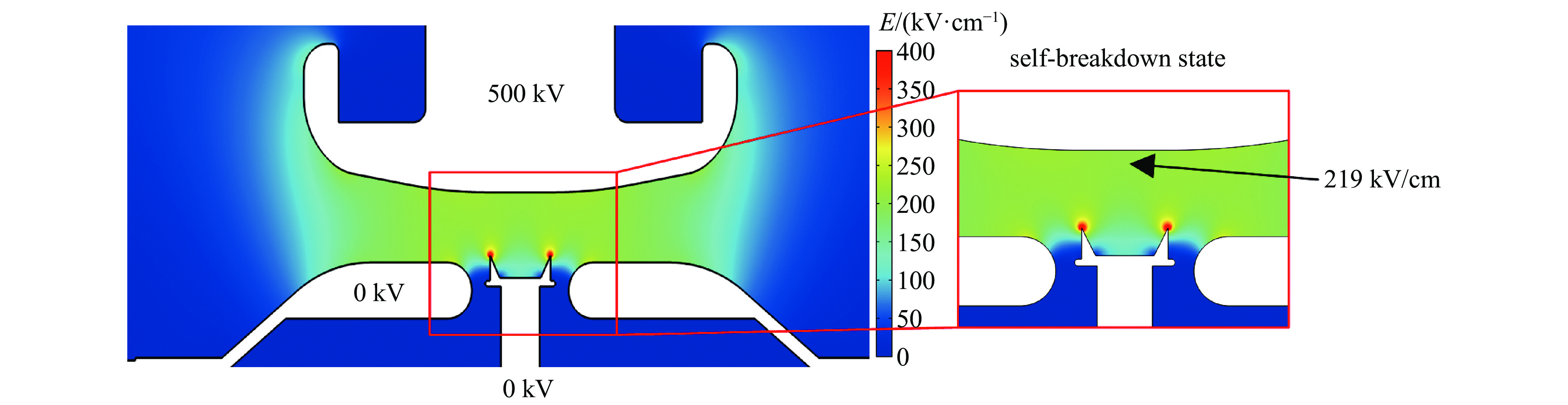
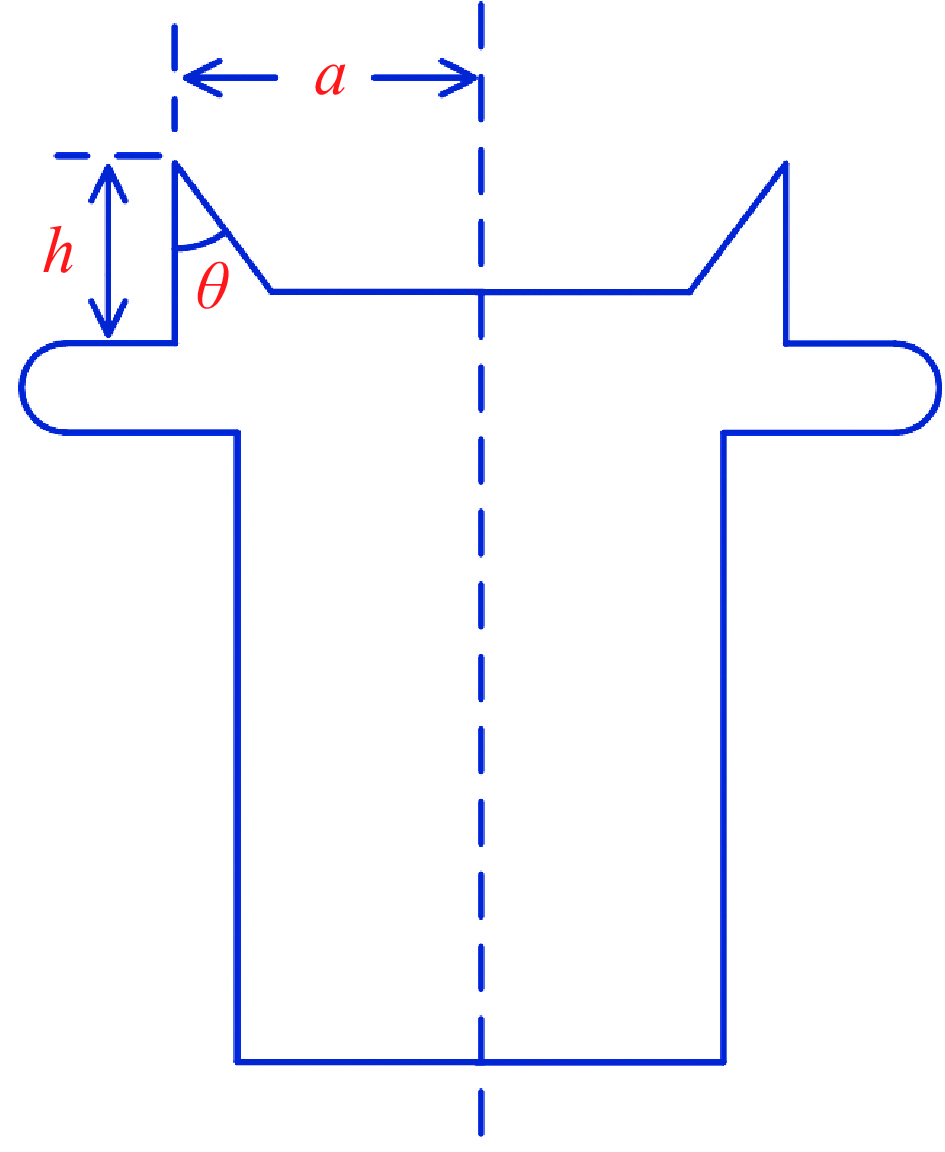
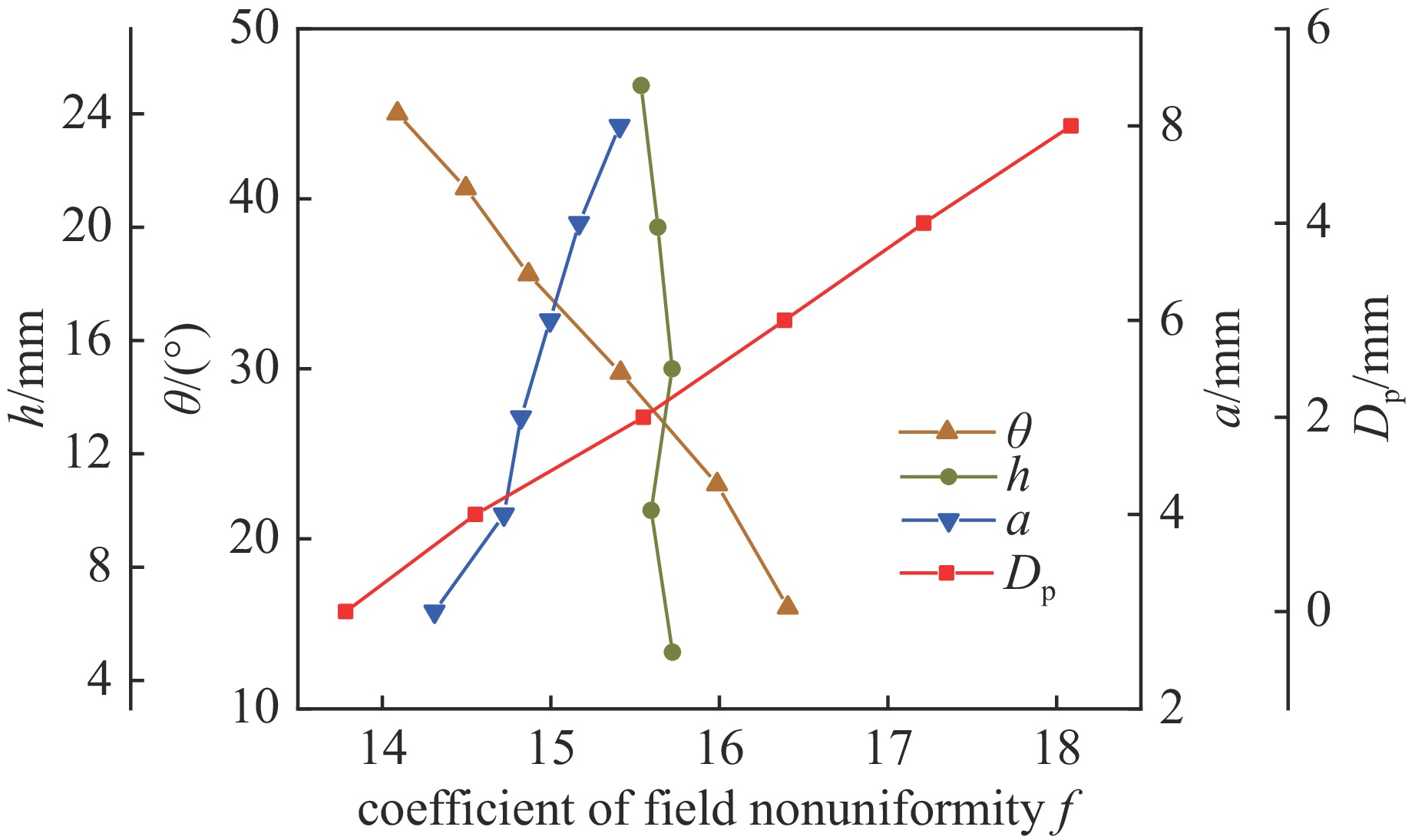
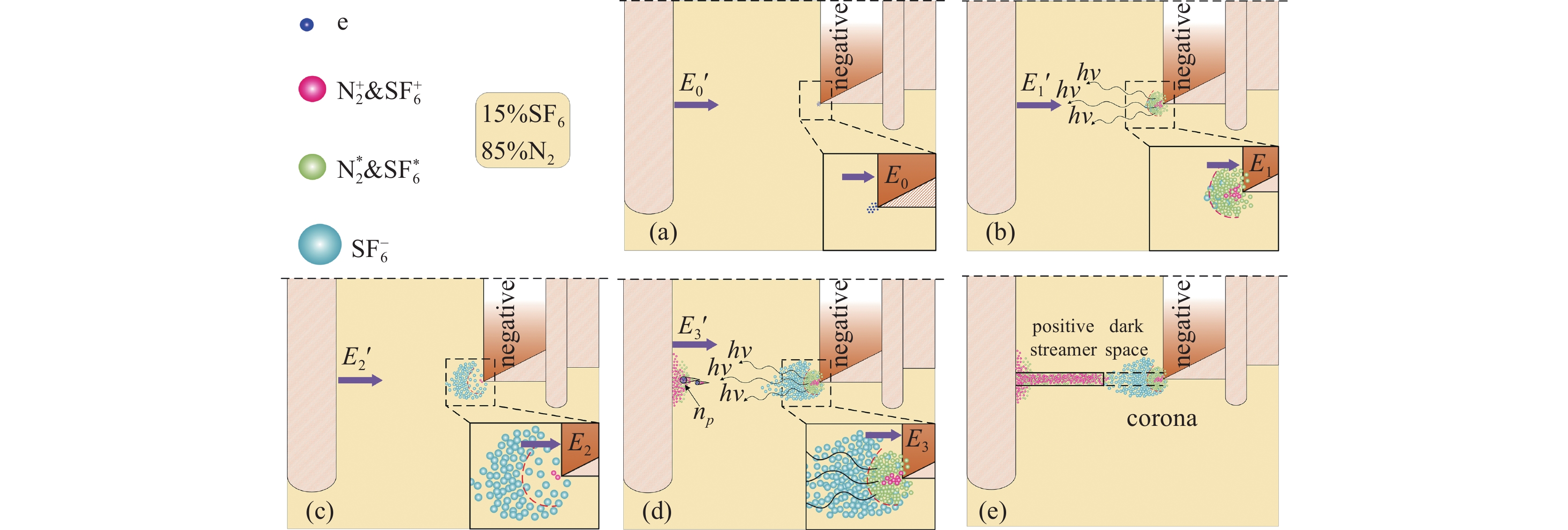
Self-breakdown stability of gas switch based on high-energy runaway electron mechanism

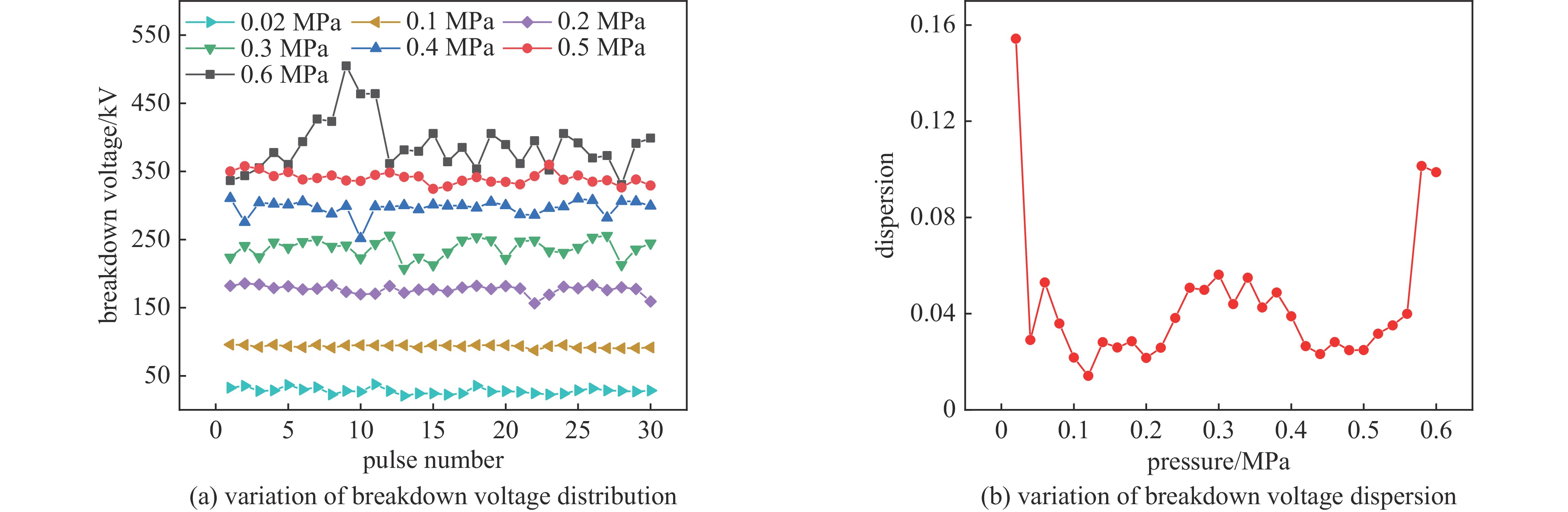
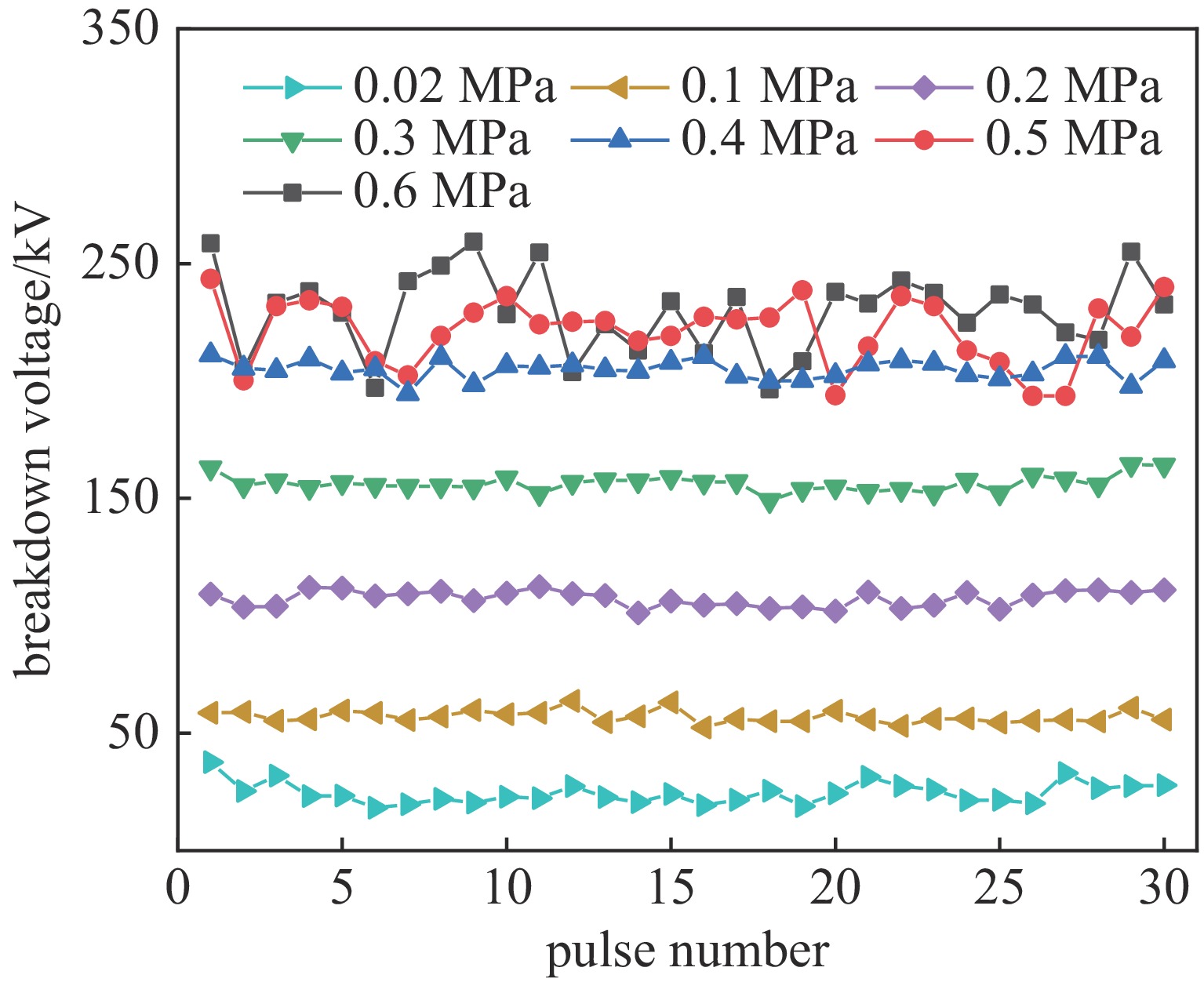
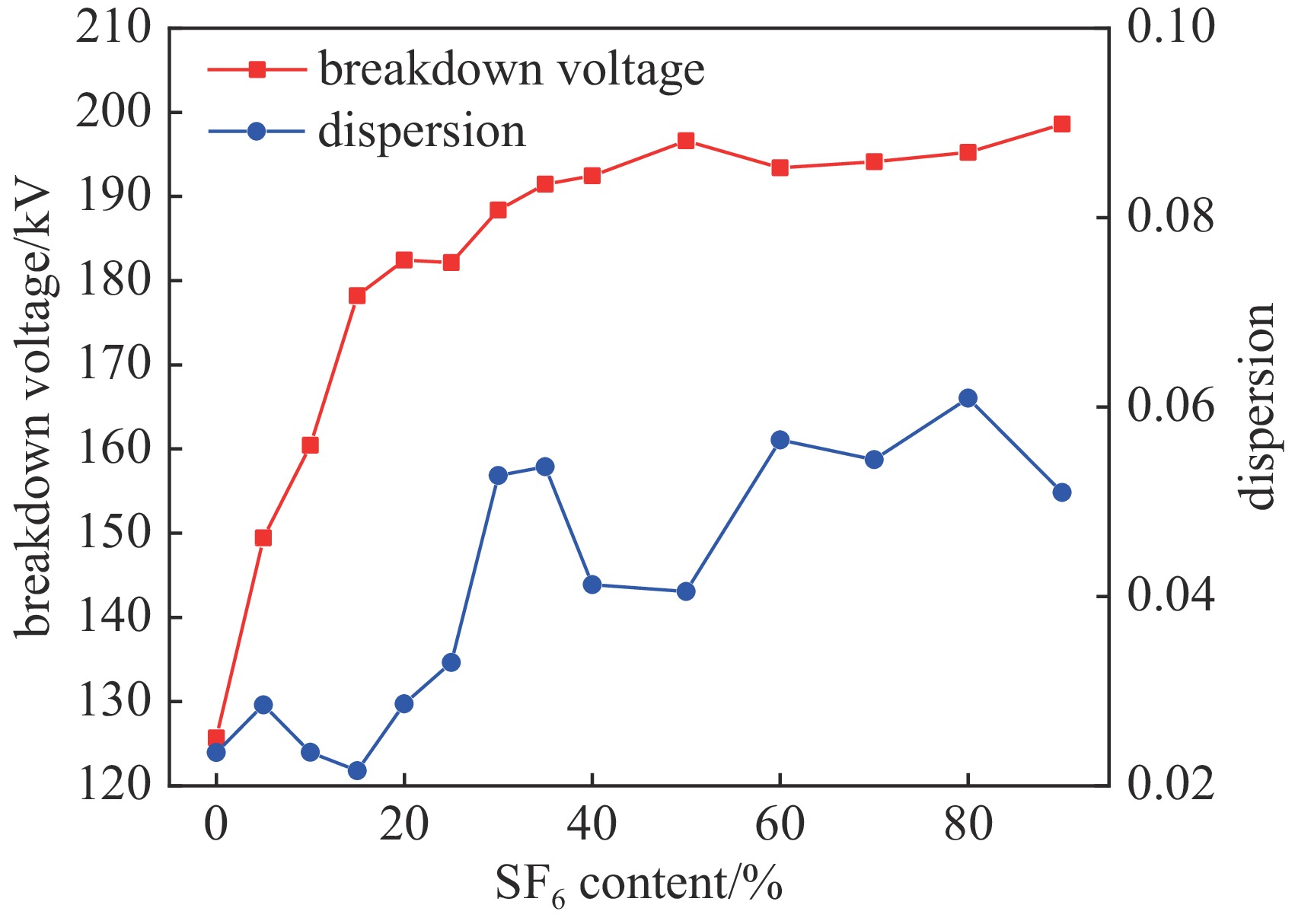
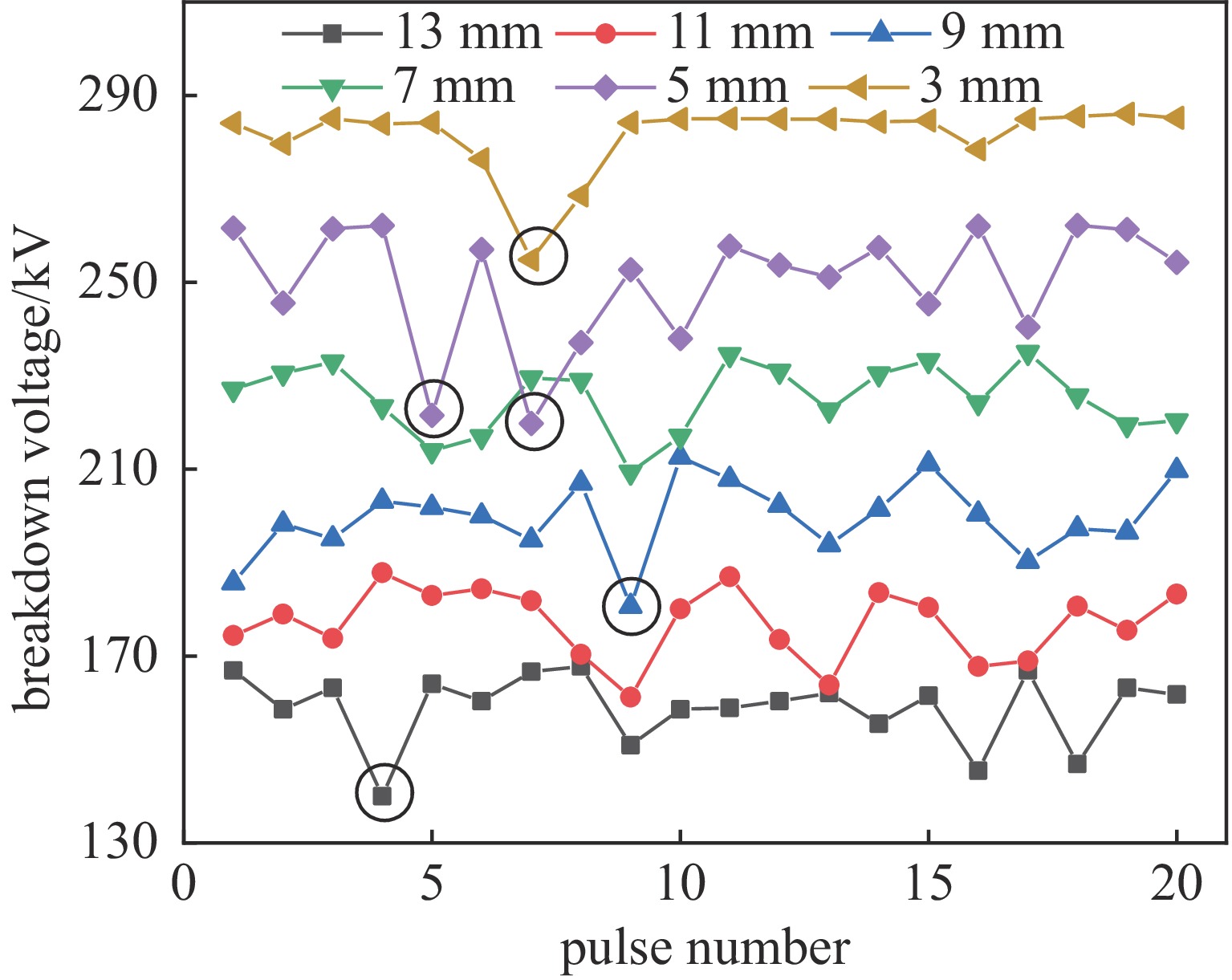
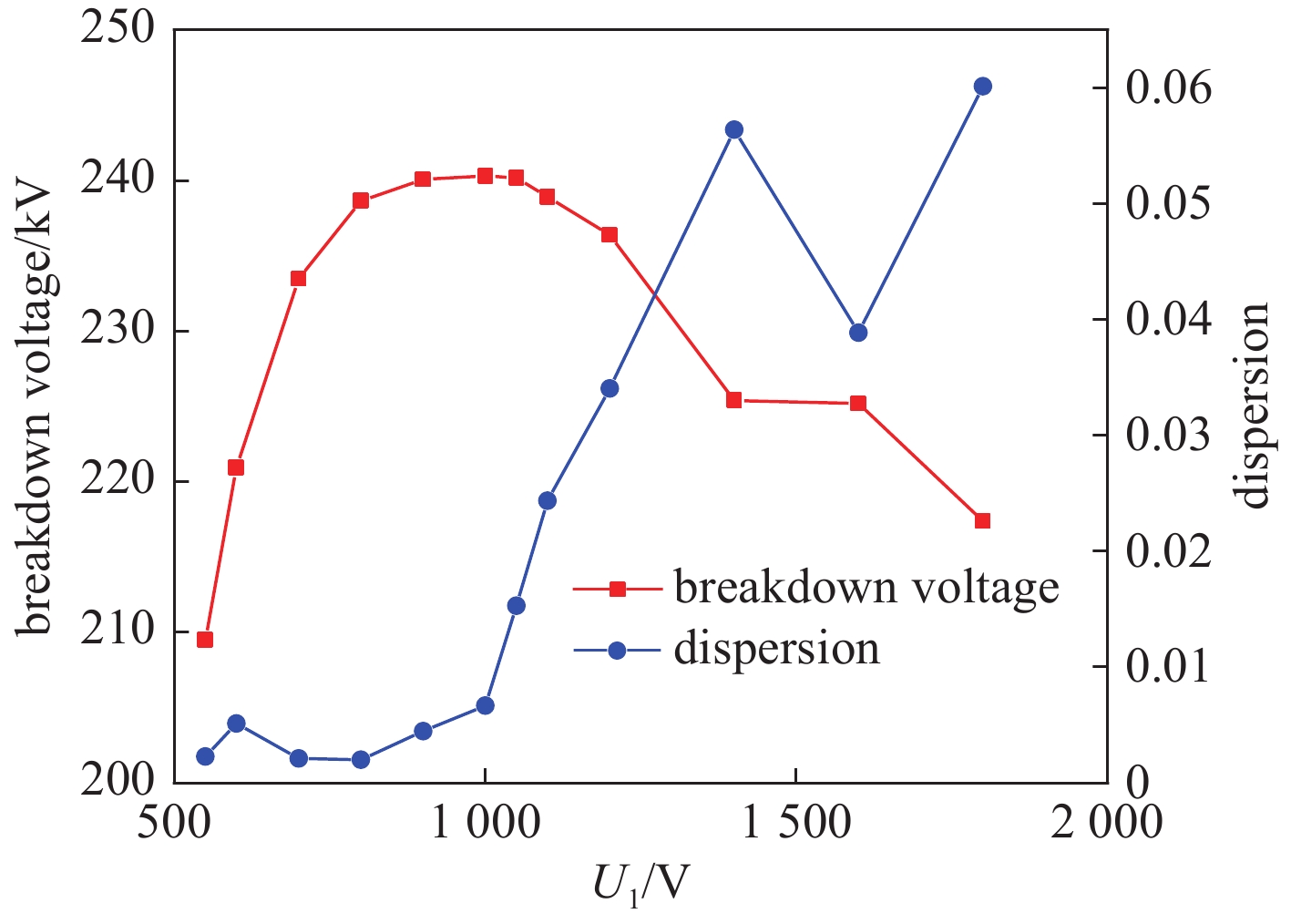
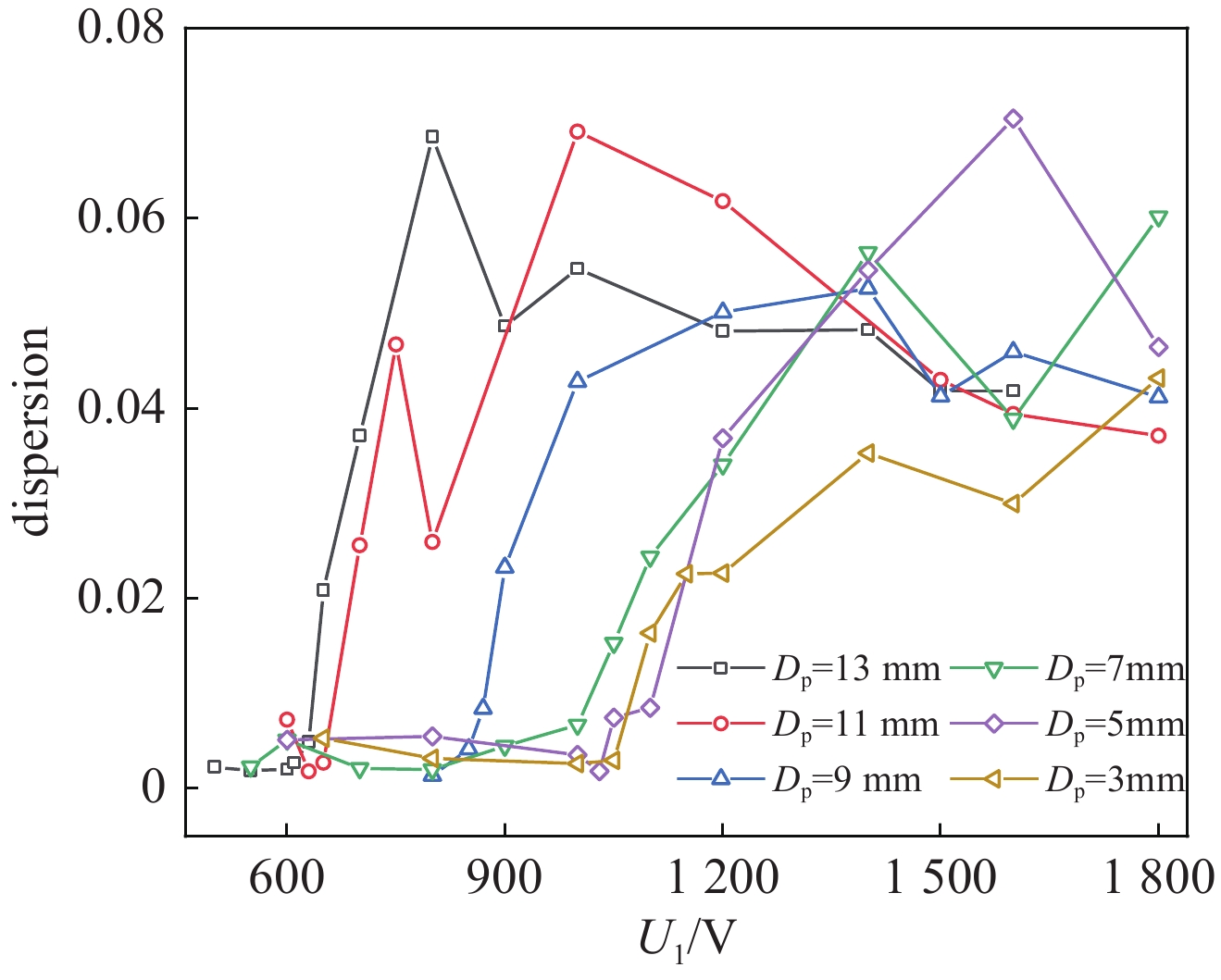
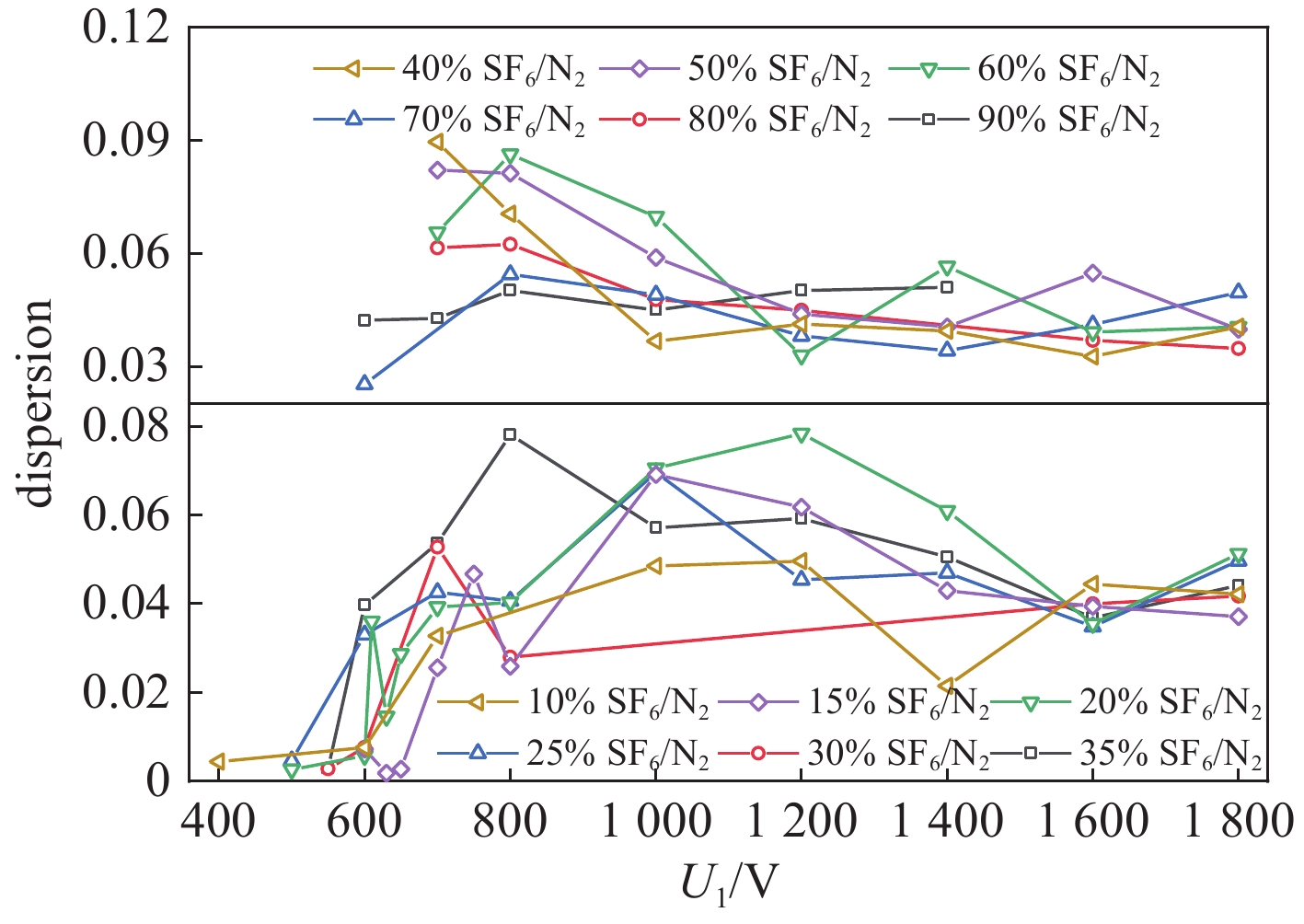
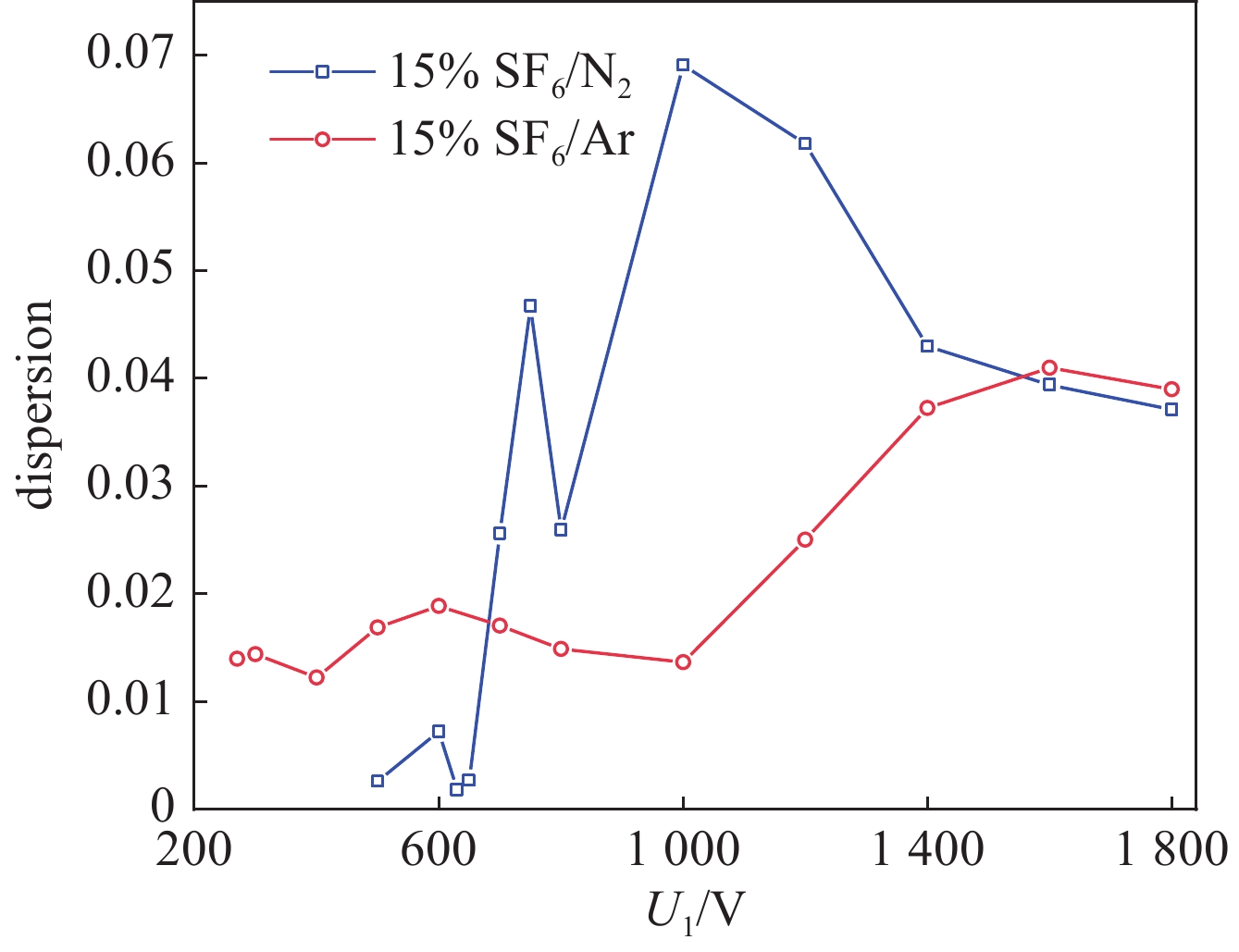
National Key Laboratory of Electromagnetic Energy, Naval University of Engineering, Wuhan 430000, China

摘要

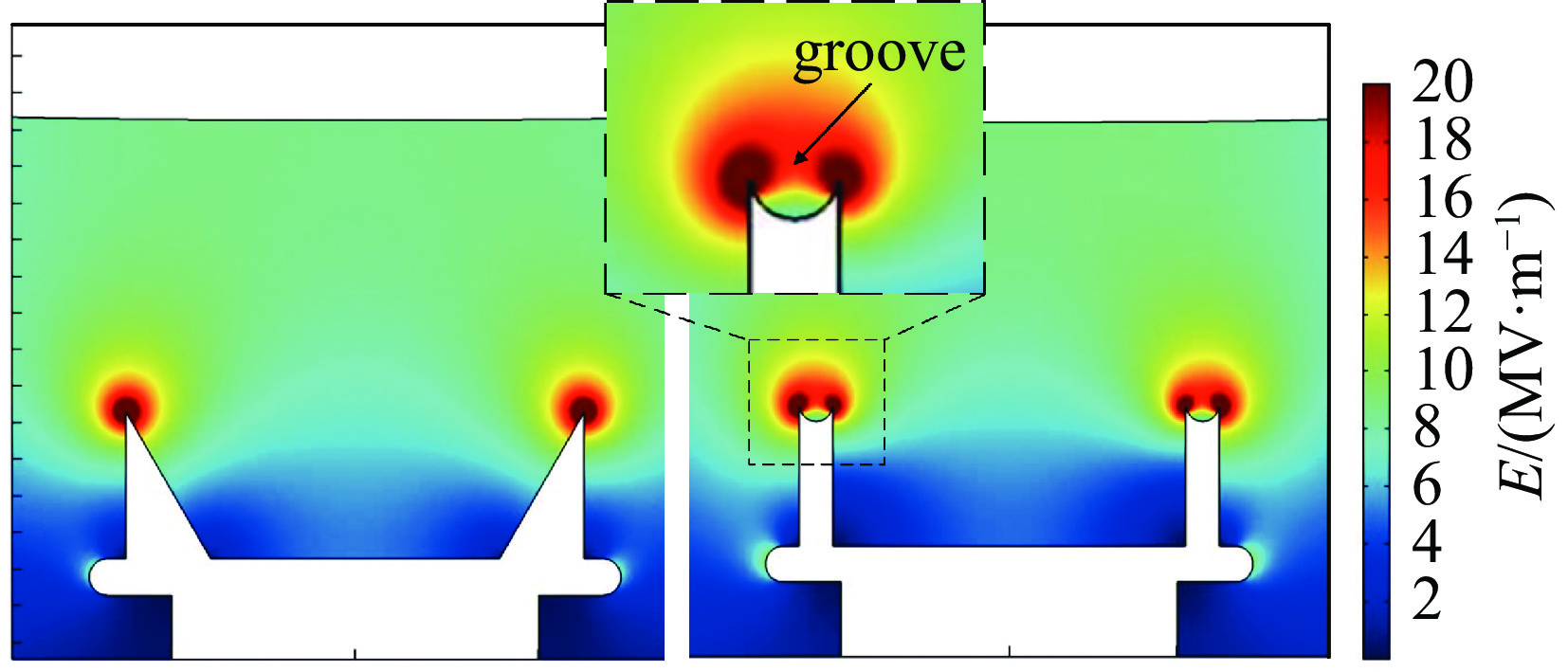
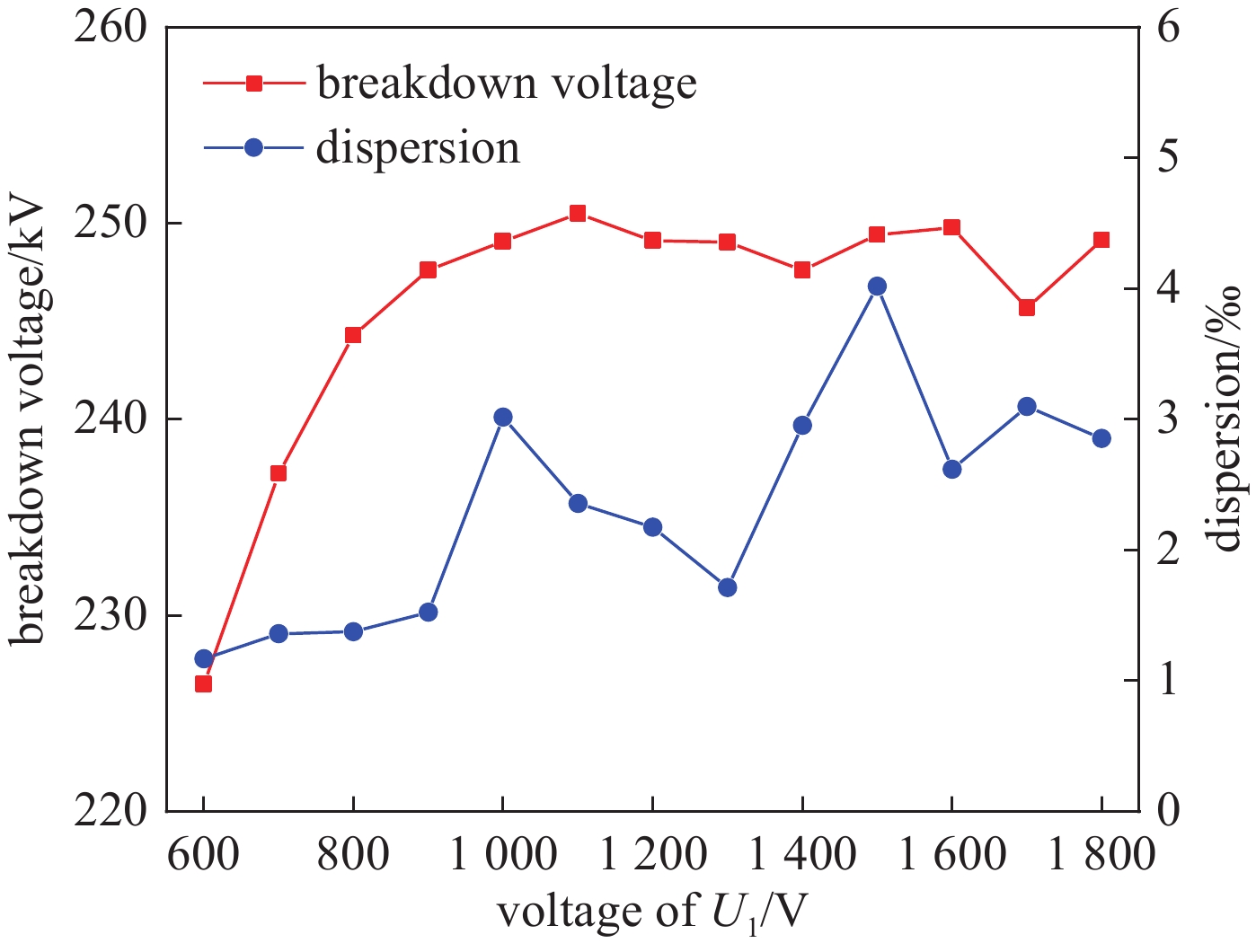
摘要: 为实现脉冲驱动源气体主开关的精确控制技术，研制了基于电晕稳定机理的气体触发开关，并对稳定电晕放电过程以及高能逃逸电子对击穿稳定性的影响进行分析，揭示了抑制高能逃逸电子产生有助于增加气体开关自击穿稳定性的机制。从气体介质和电场条件两个方面进行实验研究，对比该型气体开关的自击穿稳定性，实验结果表明：在气压0.06 MPa至0.56 MPa范围内，气体开关充15%SF₆/N₂混合气体，其自击穿离散度不超过6%，最低可达1.4%；当SF₆/N₂混合气体内的电负性气体占比小于30%时，气体开关的自击穿电压离散度保持在2%~4%范围内；在充电电压小于1800 V范围内，改变间隙内电场的时域变化速度，可降低自击穿电压的离散度，当电压上升速度为12.4 kV/μs时，自击穿电压为242 kV，离散度为0.2%；在0.3 MPa的15%SF₆/N₂混合气体内，降低触发极尖端的场不均匀系数，击穿稳定性未得到明显改善，但是在电场时域变化速度增加时，自击穿电压离散度依然可以保持在1%以下；利用沟槽型触发极代替楔形触发极，击穿电压离散度最低可达0.15%，且击穿电压稳定在248 kV附近。
- 逃逸电子 /
- 电晕稳定触发开关 /
- SF₆/N₂混合气体放电 /
- 不均匀场 /
- 脉冲功率技术
Abstract: To achieve precise control of the main triggered switch of the pulsed power source, a triggered gas switch based on the principle of corona stabilization was developed. The process of stabilized corona discharge and the influence of high-energy runaway electrons on the stability of breakdown were analyzed. This study also revealed the mechanism by which suppressing high-energy runaway electrons was beneficial in increasing the stability of gas switch self-breakdown. The experimental study was carried out from the perspectives of gas medium and E-field conditions, and the self-breakdown stability of the gas switch was compared. The self-breakdown dispersion of the gas switch filled with 15% SF₆/N₂ mixed gas was no more than 6% within the pressure of 0.06 MPa to 0.56 MPa, while the lowest value was 1.4%. The self-breakdown voltage dispersion remained within the range of 2%-4% when the electrically negative gas content in the SF₆/N₂ mixed gas was less than 30%. Within the charging voltage range of less than 1800 V, by changing the time-domain variation speed of the E-field in the gap, the self-breakdown voltage dispersion could be reduced to 0.2% with the breakdown voltage of 242 kV, while the voltage on the high voltage electrode rising speed was 12.4 kV/μs. However, reducing the field non-uniform coefficient didn`t significantly improve the breakdown stability in the 15% SF₆/N₂ mixed gas at 0.3 MPa, but the self-breakdown voltage dispersion was still kept below 1% when the voltage rising speed increased on the high voltage electrode. By replacing the wedge-shaped trigger electrode with a groove-shaped trigger electrode, the minimum self-breakdown voltage dispersion could be as low as 0.15%, and the breakdown voltage was stabilized around 248 kV.
- runaway electrons /
- corona stabilized triggered switch /
- SF₆/N₂ mixed gas discharge /
- non-uniform E-field /
- pulsed power technology

HTML全文

静止无功补偿器(SVC)相对于机械投切电容器组式的无功补偿装备，实现了无功功率精确、平滑补偿，是目前较为先进实用的无功补偿装置，已经得到了广泛应用。另外，SVC装置具有良好的分相补偿能力，对于电弧炉工作中造成的三相电压、电流不平衡有着独特的治理效果; 且晶闸管比全控型半导体开关器件造价低，有着更高的额定电压电流参数，适合拓展于高压、大容量场合。静止无功发生器(SVG)有着更快的响应时间，且可以不借助于无源支路，灵活的产生容性或感性无功功率进行调节。虽受限于目前全控型开关器件的电压容量及经济成本，然而在已经装设了SVC装置的工业现场，不改动已有的无源滤波支路，使用SVG配合SVC进行剩余无功功率补偿，具有非常大的应用拓展空间。本文针对广西某钢厂电弧炉现场，通过PSCAD/EMTDC对SVC和SVG联合方案进行了系统仿真验证^[1-4]。

1. SVC与SVG无功补偿的基本原理

工业现场SVC有多种类型，主要有五种型式：磁阀控制电抗器型(MCR型)、可控硅控制空芯电抗器型(TCR型)、可控硅阀控制高阻抗变压器型(TCT型)、可控硅开关控制电容器型(TSC型)及自饱和电抗器型(SSR型)。基本原理及仿真主要围绕TCR型SVC。而本文所述的某钢厂电弧炉现场的负荷及SVC+SVG补偿装置的电压等级均为35 kV，并联于同一条母线下。

1.1 基于斯坦门茨理论的SVC补偿原理

TCR型SVC的基本原理是以母线三相电压矢量为基准，SVC装置发出与负荷基波无功电流幅值相等、相位相反的基波电流抵消负荷无功，而无源支路的容性无功容量与负荷最大感性无功基本持平，晶闸管阀控制单元根据负荷功率的变化调控电抗器感值灵活控制SVC需要补偿的无功功率^[5]，其基本结构如图 1所示。

图 1 TCR型SVC结构图

Figure 1. TCR+FC type SVC

下载: 全尺寸图片幻灯片

根据斯坦门茨(Steinmetz, Charles Proteus)平衡化补偿原理^[6]，控制单元根据负荷无功计算出相应的电纳值，然后由电纳值推导出相应的触发角发送到晶闸管阀组。电纳值B与触发角α的关系式为

$B(\alpha)=\frac{1}{\omega L} \frac{2 \pi+\sin 2 \alpha-2 \alpha}{\pi}$

(1)

式中：ω为角频率; L为电抗值。

而斯坦门茨平衡化原理是由三相参考电压与负荷电流分别求出各相的电纳值。其基本关系式为

${B_{{\rm{ab}}}} = \frac{{\left( {{\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{bc}}}}{{\tilde{ \dot {I}}}_{{\rm{al}}}}} \right) + {\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{ca}}}}{{\tilde{ \dot {I}}}_{{\rm{bl}}}}} \right) - {\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{ab}}}}{{\tilde{ \dot {I}}}_{{\rm{cl}}}}} \right)} \right)}}{{\sqrt 3 U_{{\rm{ab}}}^2}}$

(2)

${B_{{\rm{bc}}}} = \frac{{\left( {{\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{ca}}}}{{\tilde{ \dot {I}}}_{{\rm{bl}}}}} \right) + {\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{ab}}}}{{\tilde{ \dot {I}}}_{{\rm{cl}}}}} \right) - {\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{bc}}}}{{\tilde{ \dot {I}}}_{{\rm{al}}}}} \right)} \right)}}{{\sqrt 3 U_{{\rm{bc}}}^2}}$

(3)

${B_{{\rm{ca}}}} = \frac{{\left( {{\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{ab}}}}{{\tilde{ \dot {I}}}_{{\rm{cl}}}}} \right) + {\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{bc}}}}{{\tilde{ \dot {I}}}_{{\rm{al}}}}} \right) - {\mathop{\rm Re}\nolimits} \left( {{{\dot U}_{{\rm{ca}}}}{{\tilde{ \dot {I}}}_{{\rm{bl}}}}} \right)} \right)}}{{\sqrt 3 U_{{\rm{ca}}}^2}}$

(4)

式中： ${{\dot U}_{{\rm{ab}}}}, {{\dot U}_{{\rm{bc}}}}, {{\dot U}_{ca}}$ 为母线三相参考电压矢量; ${{\tilde{ \dot {I}}}_{{\rm{al}}}}, {{\tilde{ \dot {I}}}_{{\rm{b}}1}}, {{\tilde{ \dot {I}}}_{{\rm{cl}}}}$ 是负荷三相相电流矢量。

根据斯坦门茨原理公式(2)，(3)和(4)求出的电纳B值，由式(1)查表，分别求出三相触发角，实现无功开环算法^[7]，其结构如图 2所示。

图 2 SVC控制结构框图

Figure 2. SVC control block

下载: 全尺寸图片幻灯片

1.2 基于瞬时功率理论的SVG补偿原理

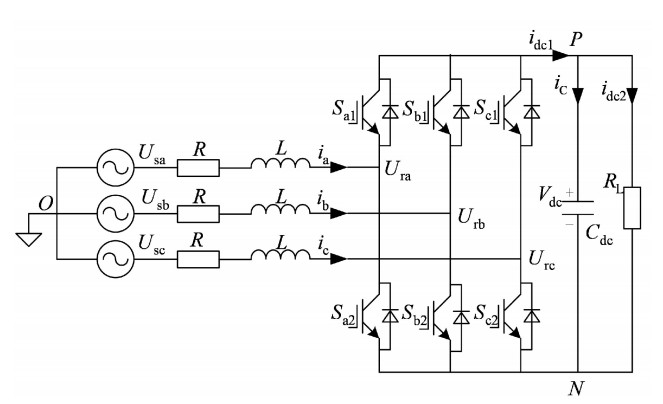
SVG，相较于基于半控型晶闸管控制的SVC装置，有着更快的响应时间。不同于根据斯坦门茨原理来计算电路的等值电纳，SVG装置使用脉冲调制技术来驱动开关管器件。而目前常用的控制技术主要有基于快速傅里叶变换的电流控制技术和基于瞬时无功功率理论的控制方法。由于基于傅里叶变换的控制技术在原理上至少存在一个周期的延时，因此在快速响应的补偿场合，大多使用基于无功功率理论的控制方法。图 3所示典型SVG逆变器的电路拓扑。

图 3 典型SVG逆变器的电路拓扑

Figure 3. Typical topology of SVG

下载: 全尺寸图片幻灯片

求解上述电路的数学模型，并将态电路函数先进行PARK变换到d-q域，然后进行拉普拉斯变换，可有

$\left\{\begin{array}{l} (s L+R) i_{\mathrm{d}}=u_{\mathrm{sd}}-u_{\mathrm{rd}}+w L i_{\mathrm{q}} \\ (s L+R) i_{\mathrm{q}}=u_{\mathrm{sq}}-u_{\mathrm{rq}}+w L i_{\mathrm{d}} \\ u_{\mathrm{dc}}=\frac{3}{2} s C\left(S_{\mathrm{d}} i_{\mathrm{d}}+S_{\mathrm{q}} i_{\mathrm{q}}\right) \end{array}\right.$

(5)

式中：i_d，i_q为i_a，i_b，i_c经过PARK变换在旋转p-q坐标系下的分量; S_a，S_b，S_c为三相桥臂的开关状态，S＝1表示该相桥臂上管开通，下管关断; S＝0表示该相下管导通，上管关断，经过p-q变换后为S_d，S_q。

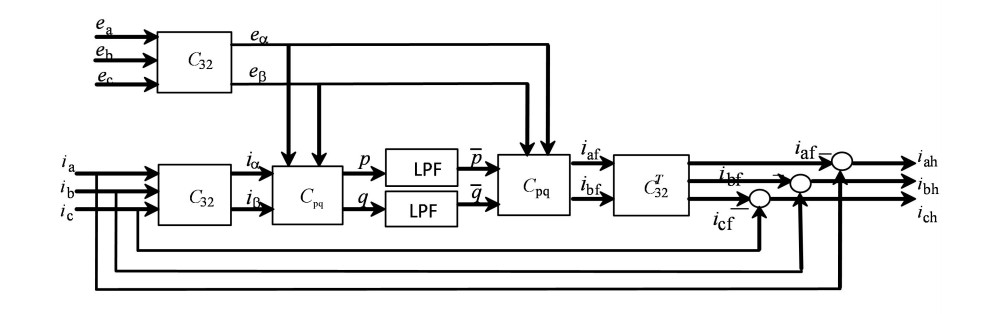
针对参考电流，根据瞬时无功功率理论，如图 4所示，先经p-q变换求出其在旋转坐标系下的直流量，然后经过低通滤波器、p-q反变换得出其基波无功电流的参考量^[8]。

图 4 基于p-q理论的谐波检测算法

Figure 4. Harmonic detection algorithm based on p-q theory

下载: 全尺寸图片幻灯片

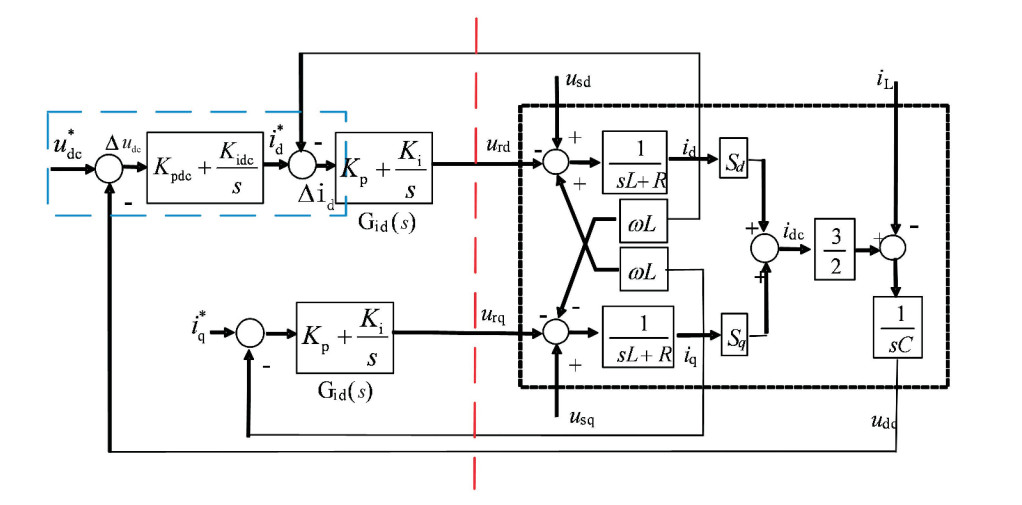
根据瞬时无功功率理论得出参考电流量后，逆变器的控制器和实际控制框图如图 5所示。

图 5 SVG逆变器的控制框图

Figure 5. Control block of SVG

下载: 全尺寸图片幻灯片

在工业现场，通常将SVG装置直接并联于负荷母线下进行无功补偿^[9-10]。本文提出的方案将SVG与SVC并联然后并联于同一母线的负荷下。

2. 广西某钢厂电弧炉的无功补偿现状

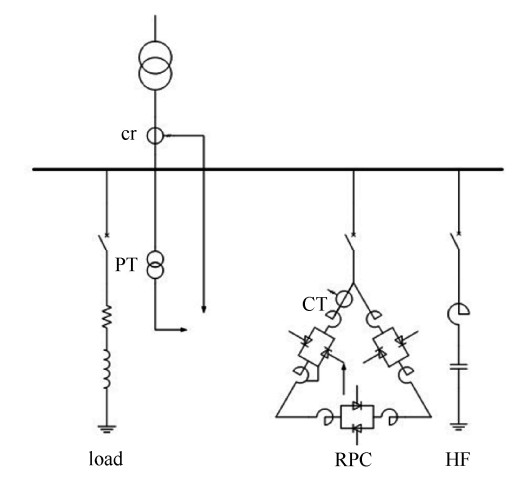
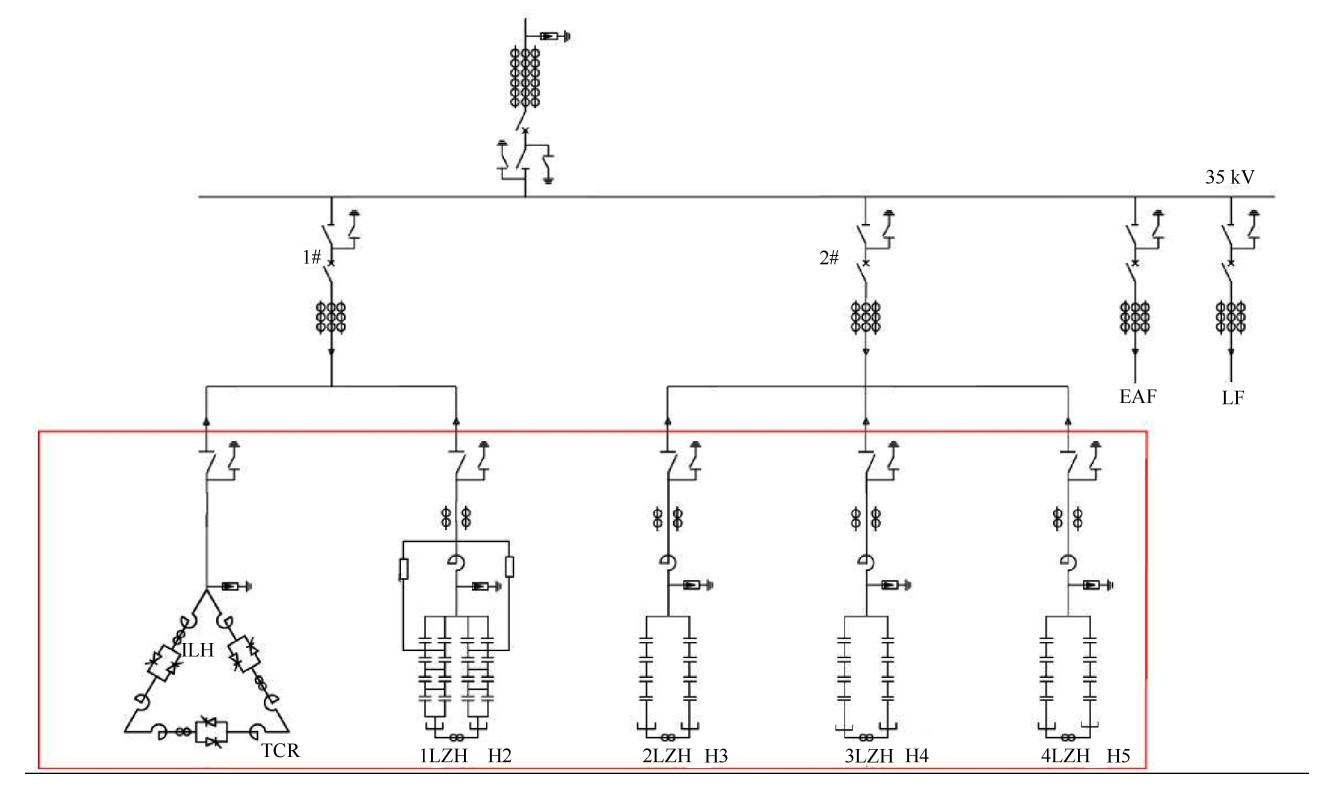
广西某钢厂110 kV高压变电站母线接入最小短路容量576 MV·A，安装50 MV·A主变压器一台，主变压器中压侧负荷主要为电弧炉和精炼炉负荷，低压侧主要为高压电动机负荷，目前场内35 kV母线侧安装TCR+FC型SVC，设置2次C型、3次、4次及5次单调谐滤波支路，总基波补偿容量25 Mvar(兆乏)，系统主接线如下图 6所示。

图 6 某钢厂电弧炉系统主接线图

Figure 6. Main topology of EAF system in a steel mill

下载: 全尺寸图片幻灯片

而该钢厂电弧炉经过改造后，发出的无功功率远超原始无功量，因此需重新计算，并于实际比对。无功需量计算应综合考虑初炼交流电弧炉(EAF)和精炼电弧炉(LF)的最大无功发生量和同时率，工程推荐值按照下式确定

$Q_{\mathrm{D}}=k_1 Q_{\mathrm{EAF}, \max }+k_2 Q_{\mathrm{L}, \mathrm{F}, \max }$

(6)

式中：k₁为EAF无功发生量的计算系数，工程推荐值为0.9~1.2;k₂为LF无功发生量的计算系数，工程推荐值为0.4~0.6;Q_{EAF, max}为EAF最大无功发生量，单位为兆乏(Mvar); Q_{LF, max}为LF最大无功发生量，单位为兆乏(Mvar); Q_D为无功需量，单位为兆乏(Mvar)。

根据计算，EAF，LF同时运行时35 kV所需最大无功发生量为35.25 Mvar。

35 kV母线所带轧机总装机容量为11 MV·A，取功率因数为0.7，功率因数提高至0.92，按公式可知

$Q=P\left(\sqrt{\frac{1}{\cos \varphi_1^2}-1}-\sqrt{\frac{1}{\cos \varphi_2^2}-1}\right)=4.57 \mathrm{Mvar}$

(7)

式中：φ₁为EAF的功率因数角; φ₂为LF的功率因数角。因此，35 kV母线总无功补偿容量为39.82 Mvar，考虑一定的补偿裕度并结合电能质量测试报告，最终确定主变35 kV母线SVC装置的基波补偿容量为40 Mvar。针对原先25 Mvar的SVC系统，出现将近15 Mvar的无功缺口。

3. 基于PSCAD/EMTDC的SVC/SVG联合应用仿真

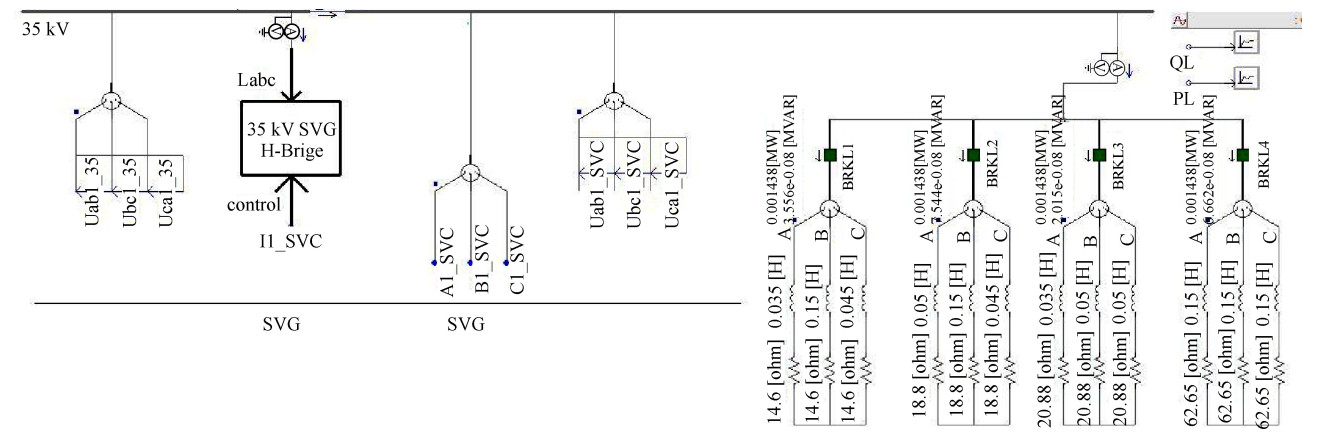
SVC具备良好的分相补偿能力，能更好适应三相不平衡工况，但响应时间较长; 而SVG有着更快响应时间。结合二者优点，针对该钢厂电弧炉现场无功补偿实际，仍可利用原先的SVC装置，由SVG填补电弧炉改造产生的增多的无功功率。将SVG单元前置与SVC单元之前，两装置独立检测、独立工作。先投入SVC及SVG装置，稳定之后一定时间内投入负荷无功源，使用PSCAD/EMTDC进行系统仿真，电弧炉负荷利用无功波动源模拟，仿真步长设为156 μs。系统的仿真结构图如图 7所示，SVG，SVC和无功波动源都接于35 kV母线。

图 7 系统仿真结构图

Figure 7. System simulation block

下载: 全尺寸图片幻灯片

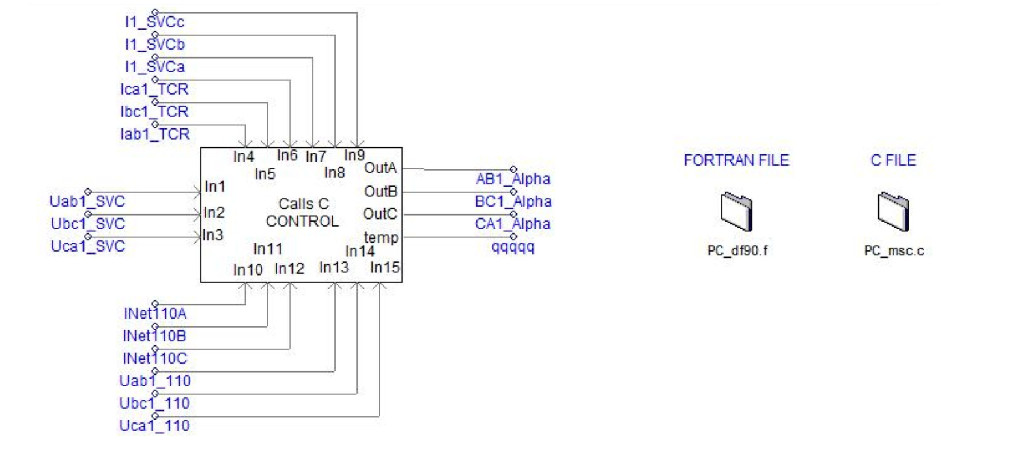
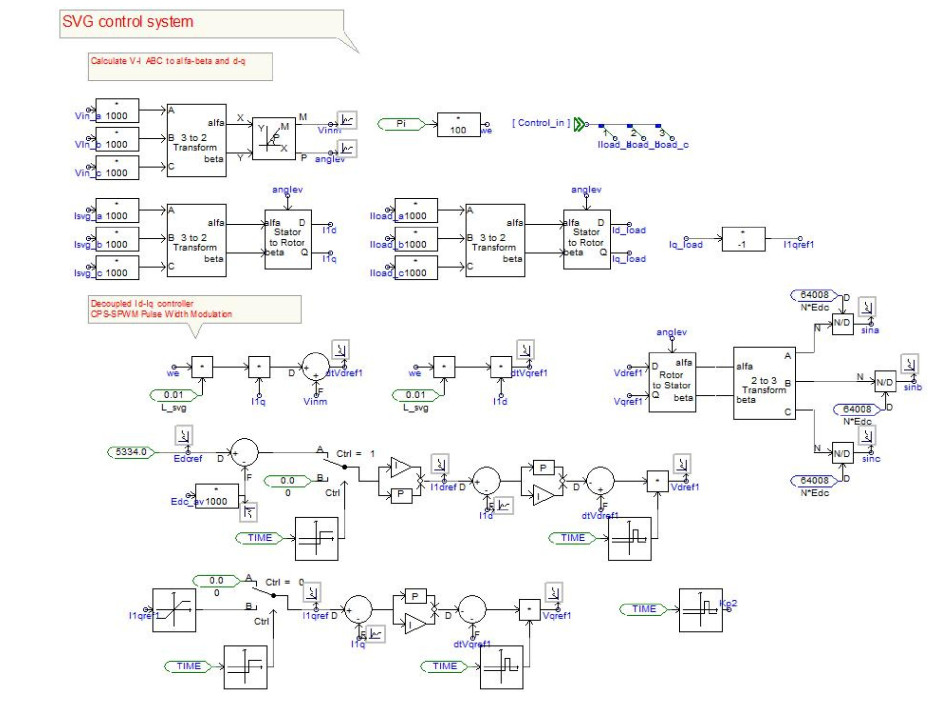
SVC控制算法是根据式(1)，(2)，(3)，(4)编写而成的C语言模块，然后由FORTRAN文件编写接口^[11-12]。而SVG单元是由基本模块串联而成的三相桥^[13]，控制模块根据式(5)及图 4、图 5所示的控制算法搭建。SVC及SVG控制模块如图 8和图 9所示。

图 8 SVC控制模块

Figure 8. SVC control block

下载: 全尺寸图片幻灯片

图 9 SVG控制模块

Figure 9. SVG control block

下载: 全尺寸图片幻灯片

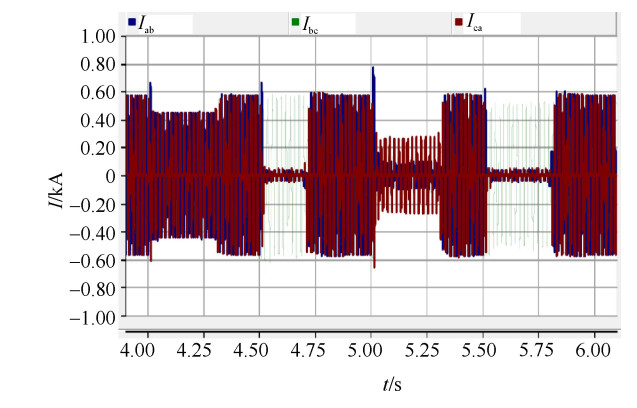
无功波动源是最大0~40 Mvar可变的三相不平衡感性无功波动源，充分模拟该钢厂的电弧炉无功功率变化。图 10为投入无功源之后TCR环内电流，可以看出三相TCR环内电流并不同步，响应了相应的不平衡。

图 10 TCR环内电流

Figure 10. Phase current of TCR

下载: 全尺寸图片幻灯片

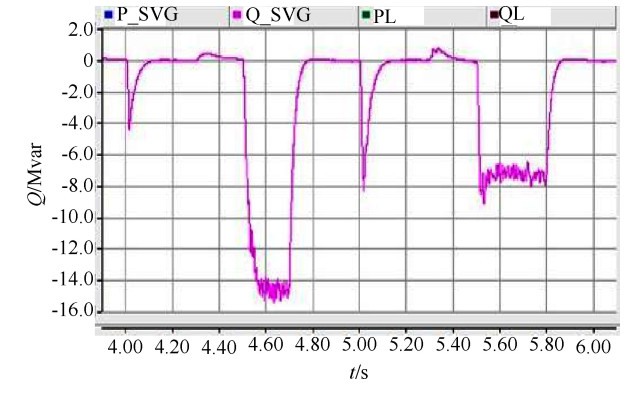
图 11为无功源投入之后，SVG发出的无功功率。SVG发出最大近16 Mvar的容性无功功率，且感性无功值基本均小于0.3 Mvar，从另一个角度可以看出SVG响应速度优异。

图 11 SVG发出的无功量

Figure 11. Reactive power generated by SVG

下载: 全尺寸图片幻灯片

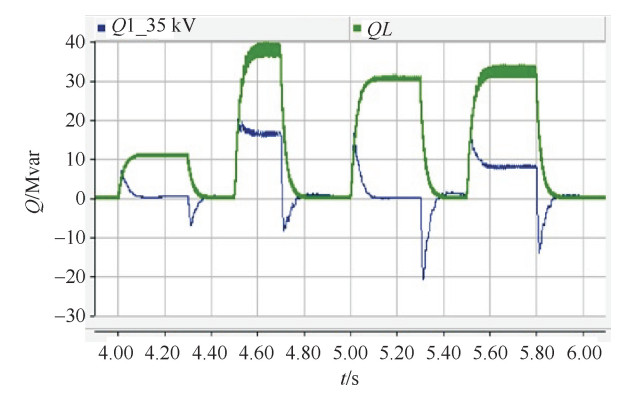
为了考察SVG补充功率的真实效果，首先投入SVC，然后投入波动无功负荷，并不投入SVG，仿真结果如图 12所示。

图 12 投入SVC，未投SVG负荷和母线的无功功率

Figure 12. Reactive power on load and grid without SVG

下载: 全尺寸图片幻灯片

在图 12中，QL为负荷无功波动源无功功率，Q1_35 kV为35 kV母线处的无功功率，在4.5 s负荷产生较大的无功波动，而此时只投入SVC，母线处仍有将近18 Mvar的感性无功，这种现象在5.5 s处负荷波动中也有类似的情况，证明在进行电弧炉改造后，SVC系统并不能完全补偿负荷的无功功率; 而在5.3s处，母线有将近20Mvar的容性无功过冲，对比图 11可知，此处的容性无功冲击在SVG并没有呈现，且不是负荷造成，因此是由于SVC不能及时响应造成的，也说明SVC较SVG响应较慢^[14-15]。

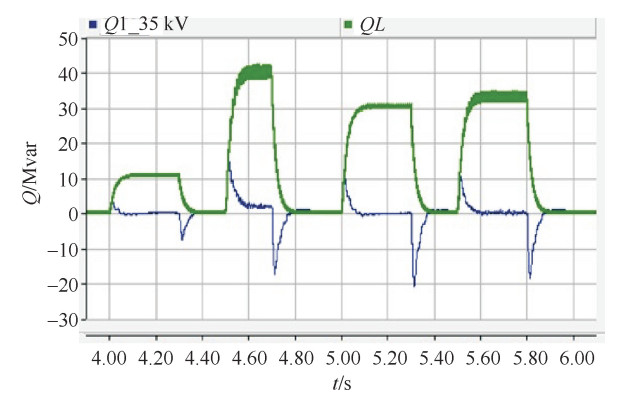
进一步将SVC和SVG联合注入后，如图 13所示。与图 12相比，在4.5 s和5.5 s处母线的无功缺口功率基本得到了抑制，结合图 11，SVG起到了快速抑制剩余无功的作用。

图 13 负荷与母线的无功功率

Figure 13. Reactive power on load and grid with SVG and SVC

下载: 全尺寸图片幻灯片

4. 结论

电弧炉现场无功补偿系统进行SVC和SVG联合应用探索，需要明确两种装置各自的功能空间，即以TCR配套FC为无功功率补偿主体，并特别针对不平衡、负序等工况; 而SVG以其优良的更快速的响应性能，承担剩余无功功率抑制的任务。在这种分工前提下，参考补偿点位置至关重要，本文提出的方案SVC装置是无法捕捉到SVG功率补偿信息，即SVG参考位置在SVC上端，进行剩余无功功率补偿。但在实际中，SVC和SVG不可能同时响应，存在一定延时，因此对于容量有限的SVG，必须做前置限幅来防止过容量补偿指令带来的系统故障保护。处理完善参考点之后进行了PACAD/EMTDC系统仿真，从仿真结果来看，SVC和SVG联合应用可以起到预定的功率补偿效果，为其向广西电弧炉现场应用提供了理论和仿真级参考。

图 1 电晕稳定触发开关结构图

Figure 1. Structure of corona stabilized triggered switch (CSTS）

下载: 全尺寸图片幻灯片

图 2 自击穿状态场位形

Figure 2. E-field configuration in self-breakdown state

下载: 全尺寸图片幻灯片

图 3 触发极结构

Figure 3. Structure of trigger electrode

下载: 全尺寸图片幻灯片

图 4 不同触发极结构参数下场不均匀系数f对比

Figure 4. Comparison of the non-uniform coefficient f of different trigger electrode structure

下载: 全尺寸图片幻灯片

图 5 极不均匀场下混合气体放电过程示意图

Figure 5. Schematic diagram of mixed gas discharge process under extremely non-uniform field

下载: 全尺寸图片幻灯片

图 6 开关自击穿实验平台电路原理图及开关高压极脉冲电压波形

Figure 6. Schematic of CSTS self-breakdown experiment and the charging voltage on HV electrode

下载: 全尺寸图片幻灯片

图 7 15%SF₆/N₂混合气体中不同气压下气体开关击穿电压分布及离散度变化

Figure 7. Variation of breakdown voltage distribution and dispersion of gas switch under different pressure in 15%SF₆/N₂ gas mixture

下载: 全尺寸图片幻灯片

图 8 15%SF6/Ar混合气体中不同气压下气体开关击穿电压分布

Figure 8. 15% breakdown voltage distribution of gas switch under different pressure in SF₆/Ar gas mixture

下载: 全尺寸图片幻灯片

图 9 SF₆/N₂中不同SF₆占比对击穿电压及其离散度的影响

Figure 9. Influence of SF₆ ratio on breakdown voltage and dispersion in SF₆/N₂ gas mixture

下载: 全尺寸图片幻灯片

图 10 不同D_p下开关自击穿电压分布

Figure 10. Distribution of self-breakdown voltage under different D_p

下载: 全尺寸图片幻灯片

图 11 不同U₁下的平均自击穿电压及其离散变化

Figure 11. Variation of average self-breakdown voltage and dispersion under different U₁

下载: 全尺寸图片幻灯片

图 12 不同D_p下击穿电压离散度对电压U₁的变化关系

Figure 12. Variation of the breakdown voltage dispersion with voltage U₁ under different D_p

下载: 全尺寸图片幻灯片

图 13 不同SF₆占比下气体开关自击穿离散度随电压U₁的变化

Figure 13. Variation of the breakdown voltage dispersion with voltage U₁ under different SF₆ proportion

下载: 全尺寸图片幻灯片

图 14 SF₆与N₂和Ar混合气体中气体开关自击穿离散度随电压U₁的变化

Figure 14. Variation of the breakdown voltage dispersion with voltage U₁ in gas mixture of SF₆, N₂ and Ar

下载: 全尺寸图片幻灯片

图 15 电晕稳定阶段高能RAEs示意图

Figure 15. Schematic diagram of high-energy RAEs during corona stabilization stage

下载: 全尺寸图片幻灯片

图 16 楔形触发极和沟槽型触发极场位形结构对比

Figure 16. Comparison of E-field configuration between wedge-shaped trigger and groove-shaped trigger

下载: 全尺寸图片幻灯片

图 17 沟槽型触发极20次重复频率自击穿典型波形，U₁=1 300 V，D_p=5 mm

Figure 17. Typical breakdown waveform of 20 pulses of groove trigger, U₁=1 300 V, D_p=5 mm

下载: 全尺寸图片幻灯片

图 18 沟槽型触发极的自击穿电压及离散度随U₁变化

Figure 18. Variation of the self-breakdown voltage and dispersion of the groove-shaped trigger with U₁

下载: 全尺寸图片幻灯片

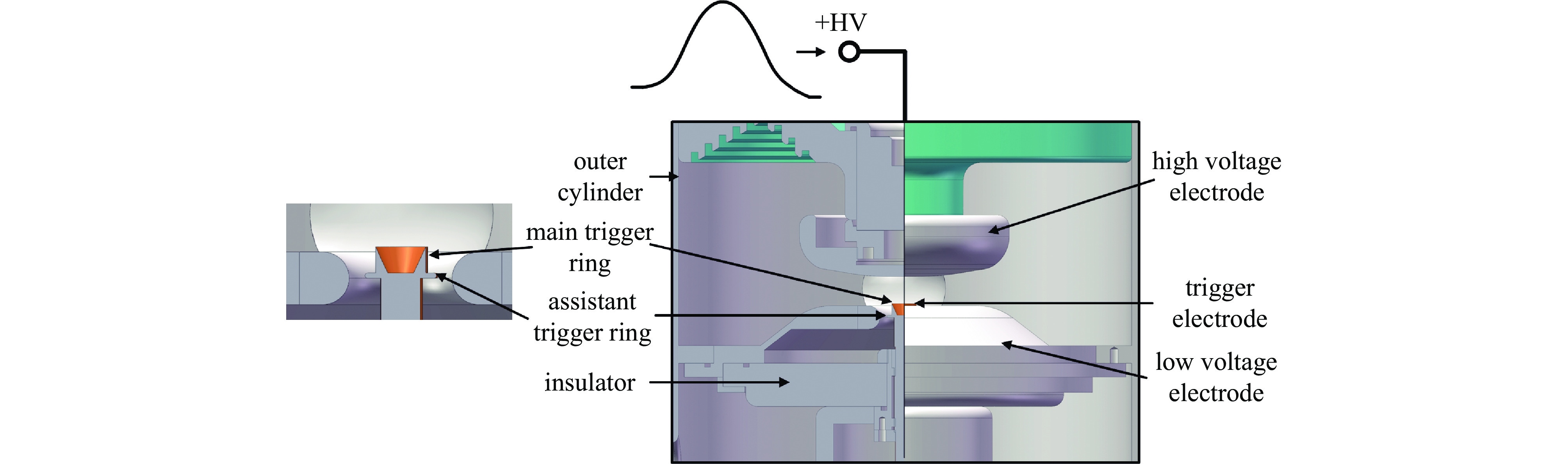
表 1 电晕稳定触发开关主要结构参数

Table 1. Main parameters of the CSTS

main gap length/cm	low voltage electrode outer radius/cm	low voltage electrode inner radius/cm	main trigger ring radius/cm	assistant trigger ring radius/cm	main trigger ring height/cm	outer cylinder radius/cm
2.65	7.5	2	1.25	1.45	1	20

下载: 导出CSV

参考文献(15)

[1]	张嘉焱, 舒挺, 袁成卫. 高功率微波空间功率合成的初步研究[J]. 强激光与粒子束, 2007, 19(6):915-918 Zhang Jiayan, Shu Ting, Yuan Chengwei. Primary study on spatial powers combining of parallel and intersectant beams of high power microwave[J]. High Power Laser and Particle Beams, 2007, 19(6): 915-918
[2]	Granatstein V L, Parker R K, Armstrong C M. Vacuum electronics at the dawn of the twenty-first century[J]. Proceedings of the IEEE, 1999, 87(5): 702-716. doi: 10.1109/5.757251
[3]	Liu Zhenbang, Song Falun, Jin Hui, et al. Coherent combination of power in space with two X-band gigawatt coaxial multi-beam relativistic klystron amplifiers[J]. IEEE Electron Device Letters, 2022, 43(2): 284-287. doi: 10.1109/LED.2021.3137927
[4]	MacGregor S J, Turnbull S M, Tuema F A, et al. A 100 kV, 1 kHz triggered pulse generator[C]//Proceedings of 1996 International Power Modulator Symposium. 1996: 153-156.
[5]	Beveridge J R, Macgregor S J, Timoshkin I V, et al. A corona-stabilised plasma closing switch[C]//IEEE International Power Modulators and High-Voltage Conference, 2008: 487-490.
[6]	Larsson A, Yap D, Lim Y W. Time jitter study of a corona-stabilized closing switch[J]. IEEE Transactions on Plasma Science, 2012, 40(10): 2646-2652. doi: 10.1109/TPS.2012.2208103
[7]	Liang Tianxue, Jiang Xiaofeng, Wang Zhiguo, et al. Characteristics study of multigaps gas switch with corona discharge for voltage balance[J]. IEEE Transactions on Plasma Science, 2014, 42(2): 340-345. doi: 10.1109/TPS.2013.2295096
[8]	Gao Pengcheng, Su Jiancang, Zeng Bo, et al. A low-jitter self-break repetitive multi-stage gas switch[J]. Review of Scientific Instruments, 2017, 88: 024705. doi: 10.1063/1.4973420
[9]	Tarasenko V F, Zhang Cheng, Baksht E K, et al. Review of supershort avalanche electron beam during nanosecond-pulse discharges in some gases[J]. Matter and Radiation at Extremes, 2017, 2(3): 105-116. doi: 10.1016/j.mre.2016.10.004
[10]	邵涛. 重复频率纳秒脉冲气体击穿研究[D]. 北京: 中国科学院研究生院(电工研究所), 2006: 60-88 Shao Tao. Study on repetitive nanoseeond-pulse breakdown in gases[D]. Beijing: Graduate School of the Chinese Academy of Sciences, 2006: 60-88
[11]	Stankevich Y L, Kalinin V G. Fast electrons and X-ray radiation during the initial stage of growth of a pulsed spark discharge in air[J]. Soviet Physics Doklady, 1968, 12: 1042.
[12]	Gurevich A V, Milikh G M, Roussel-Dupre R. Runaway electron mechanism of air breakdown and preconditioning during a thunderstorm[J]. Physics Letters A, 1992, 165(5/6): 463-468.
[13]	邵涛, 章程, 王瑞雪, 等. 大气压脉冲气体放电与等离子体应用[J]. 高电压技术, 2016, 42(3):685-705 Shao Tao, Zhang Cheng, Wang Ruixue, et al. Atmospheric-pressure pulsed gas discharge and pulsed plasma application[J]. High Voltage Engineering, 2016, 42(3): 685-705
[14]	Shea J J. Physics of pulsed breakdown in gases[J]. IEEE Electrical Insulation Magazine, 2001, 17(5): 60-61.
[15]	耿玖源, 杨建华, 舒挺, 等. 10 GW甘油介质双螺旋Blumlein脉冲形成线[J]. 强激光与粒子束, 2023, 35:065004 doi: 10.11884/HPLPB202335.230005 Geng Jiuyuan, Yang Jianhua, Shu Ting, et al. 10 GW dual-spiral Blumlein pulse forming lines in glycerol medium[J]. High Power Laser and Particle Beams, 2023, 35: 065004 doi: 10.11884/HPLPB202335.230005

施引文献

期刊类型引用(4)

1.	黄港，王祖军，吕伟，聂栩，赖善坤，晏石兴，王敏文，卓鑫，于俊英，王忠明. 不同能量质子辐照诱发CCD图像传感器性能退化实验与分析. 光学学报. 2023(11): 201-208 . 百度学术
2.	王兴鸿，王祖军，蔡星会，尹利元，唐宁，晏石兴，李传洲. 光电半导体材料辐照诱发微观缺陷的演化特性研究. 半导体光电. 2023(06): 869-875 . 百度学术
3.	谭群，范杰清，赵强，张芳，李尧，郝建红，董志伟. CCD电子辐照效应三维蒙特卡罗模拟研究. 强激光与粒子束. 2022(04): 115-120 . 本站查看
4.	丁曼. γ射线作用下氧化铪基MOS结构总剂量效应研究. 强激光与粒子束. 2019(06): 118-122 . 本站查看

其他类型引用(2)

资源附件(0)

访问统计

点击查看大图

图(18) / 表(1)

计量

文章访问数: 227
HTML全文浏览量: 65
PDF下载量: 30
被引次数: 6

1. SVC与SVG无功补偿的基本原理
1.1 基于斯坦门茨理论的SVC补偿原理
1.2 基于瞬时功率理论的SVG补偿原理
2. 广西某钢厂电弧炉的无功补偿现状
3. 基于PSCAD/EMTDC的SVC/SVG联合应用仿真
4. 结论

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

基于高能逃逸电子机制的气体开关自击穿稳定性

doi: 10.11884/HPLPB202436.240305

作者简介:
耿玖源，gengjiuyuan@foxmail.com

计量

Self-breakdown stability of gas switch based on high-energy runaway electron mechanism

1. SVC与SVG无功补偿的基本原理

1.1 基于斯坦门茨理论的SVC补偿原理

1.2 基于瞬时功率理论的SVG补偿原理

2. 广西某钢厂电弧炉的无功补偿现状

3. 基于PSCAD/EMTDC的SVC/SVG联合应用仿真

4. 结论

期刊类型引用(4)

其他类型引用(2)

计量

目录

1. SVC与SVG无功补偿的基本原理

1.1 基于斯坦门茨理论的SVC补偿原理

1.2 基于瞬时功率理论的SVG补偿原理

2. 广西某钢厂电弧炉的无功补偿现状

3. 基于PSCAD/EMTDC的SVC/SVG联合应用仿真

4. 结论

留言板

基于高能逃逸电子机制的气体开关自击穿稳定性

doi: 10.11884/HPLPB202436.240305

作者简介: 耿玖源，gengjiuyuan@foxmail.com

计量

出版历程

Self-breakdown stability of gas switch based on high-energy runaway electron mechanism

1. SVC与SVG无功补偿的基本原理

1.1 基于斯坦门茨理论的SVC补偿原理

1.2 基于瞬时功率理论的SVG补偿原理

2. 广西某钢厂电弧炉的无功补偿现状

3. 基于PSCAD/EMTDC的SVC/SVG联合应用仿真

4. 结论

期刊类型引用(4)

其他类型引用(2)

计量

出版历程

目录

1. SVC与SVG无功补偿的基本原理

1.1 基于斯坦门茨理论的SVC补偿原理

1.2 基于瞬时功率理论的SVG补偿原理

2. 广西某钢厂电弧炉的无功补偿现状

3. 基于PSCAD/EMTDC的SVC/SVG联合应用仿真

4. 结论

作者简介:
耿玖源，gengjiuyuan@foxmail.com