High average power spectral beam combining employing volume Bragg gratings
-
摘要: 使用透射型体布拉格光栅组束两束光纤激光,实现了856 W光谱组束输出。总的光谱组束效率为73.7%,组束光束的横向质量因子为7.9,纵向质量因子为2.7。研究结果显示,虽然体光栅的角色散严重影响衍射光束的光束质量,但其并不影响透射光束的光束特性。由于当前宽谱光纤激光器的输出功率远大于窄线宽输出,使用宽谱光纤激光器(光谱带宽超过4 nm)作为透射光束,能够在不降低组束效率和组束光束质量的前提下,有效提升使用体布拉格光栅进行光谱组束的总输出功率。Abstract: We have achieved 856 W spectral beam combining output of two fiber lasers employing a transmitting volume Bragg grating (TVBG), which is the highest combining power of spectral beam combination by VBGs. The total spectral combining efficiency is 73.7% and the beam quality of combining beam is 7.9 and 2.7 in x and y direction, respectively. Though the diffraction beam is seriously stretched by angular dispersion of TVBG, the transmission beam preserves its beam properties in the high average power spectral beam combining. This indicates that the broadband fiber lasers (the spectral bandwidth is over 4 nm) can be used as transmission beam in high efficiency spectral beam combination of VBGs for higher combining power output.
-
Key words:
- laser beam combining /
- spectral beam combining /
- volume gratings /
- diffraction efficiency /
- beam quality
-
增材制造(AM)技术是指将计算机辅助设计的构件模型按照一定厚度进行切片分层,然后将粉末或丝材采用逐层熔化叠加方式制造出具有复杂几何形状零部件的一种近净成形工艺[1]。选区激光熔化(SLM)技术是AM技术中较为成熟的一种方式,是一种以激光为能量源的增材制造技术,SLM成形具有结构件精度高,成形零部件不受结构复杂度限制,能直接成形零部件等优势[2]。
SLM增材制造过程中,在激光快速扫描经过金属粉末时,金属粉末迅速升温从而熔化形成熔池,由固相变为液相,然后再迅速降温,熔池冷却凝固由液相变为固相。熔池在快速熔化快速凝固的过程中温差较大,温度梯度较高,形成不均匀的温度场,在凝固及冷却收缩过程中极易形成较大的残余应力。残余应力是一种内应力,内应力较大时将影响金属构件机械强度,产生较大变形,严重时还会产生缺陷或者裂纹[3-4]。
研究发现,SLM工艺参数对残余应力影响较大,其中激光功率、扫描速度、扫描路径、铺粉层厚以及粉末预热温度等因素影响尤为明显[5-7],而这些参数相互耦合在一起,具有非线性特点。龚丞等人[3]研究了不同工艺参量时残余应力的分布规律;杨健等人[4]研究了扫描方式和堆积层数对残余应力的影响;李九霄等人[6]介绍了SLM制造过程中残余应力的产生机制和检测方法,综述了SLM工艺参数对残余应力的影响。
利用有限元分析软件进行数值模拟是预测残余应力常用的方法。数值模拟方法的优点是成本较低、效率较高、数据量较大,并且能够分析出SLM整个过程的关键数据。然而,数值模拟需要对SLM成形过程中热源模型、金属粉末特性热传导性、熔池行为等工作条件进行理想化处理,而实际上,这些理想化处理的条件,会对实验结果产生一定的影响。因此,目前对模拟方法和模型建立等方面的研究仍然不成熟,还未形成统一的建立模型的标准或规则[8]。
神经网络可以对高度非线性函数进行逼近,通过对已知样本进行自适应学习,找到输出量与输入量的关系,其容错能力和非线性信息并行处理能力都较高,适用于不确定复杂非线性系统模型的建模方法,得到了广泛应用。尤其是利用神经网络确定输入参数与输出参数之间的关系模型,在优化SLM工艺参数方面具有很大优势[9-11]。Akbari M等人[10]开发了不同的人工神经网络,用于焊接熔池温度分布和焊缝几何形状的逐步预测,降低了成本,缩短了时间。雷凯明等人[12]利用遗传算法优化BP神经网络初始的权值和阈值,建立激光熔覆工艺参数与熔池特征参数之间的网络预测模型,实现熔池特征参数的精确预测。姜淑娟等人[13]建立利用激光工艺参数预测熔覆高度的误差BP神经网络模型,验证了该预测模型在理论和实践上的可行性与有效性。
1. 实 验
1.1 实验思路与采用设备
实验采用英国Renishaw公司的生产的AM400型号选区激光熔化系统制备试样,对试样残余应力影响较大的激光功率、扫描速度、铺粉层厚以及粉末预热温度等关键参数采用正交方法进行设置。材料选用316L不锈钢粉末,其成分如表1所示。
表 1 316L不锈钢粉末化学成分比重Table 1. Chemical composition of 316L stainless steel by weightelement content/% element content/% Fe balance N 0.1max Cr 16~18 O 0.1max Ni 10~14 P 0.045max Mo 2~3 C 0.03max Mn 2max S 0.03max Si 1max 采用Phenom XL扫描电镜观察不同参数制备试样的微观结构,首先从微观结构上分析不同参数对试样残余应力的影响。采用HXT-M-72残余应力测试仪对试样进行残余应力测定,得到不同参数对应的残余应力值。将试样的工艺参数作为输入,残余应力值作为输出,输入到BP神经网络模型进行训练,得到预测模型。用此模型预测试样残余应力,并与实际测量值进行对比,验证神经网络预测模型的可靠性。
1.2 实验理论依据和实验方法、模型的确定
1.2.1 超声波检测残余应力基本理论与方法
目前测量SLM工件残余应力的方法主要为间接方法,常用的方法有盲孔法、X射线衍射法、超声波法。
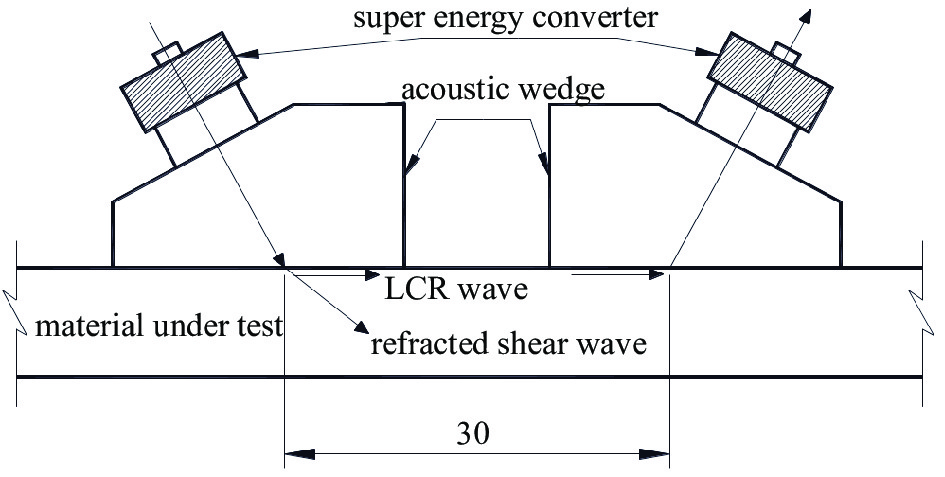
盲孔法为有损检测法,对被测工件具有破坏性,无法进行后续的力学拉伸实验,工件制作成本较高,造成较大浪费。X射线衍射法为无损检测方法,但检测深度较浅,且如果工件和靶含有相同元素,测量结果会受到较大干扰,316L不锈钢Cr含量较高,使用Cr靶仪器就很难测出残余应力值。超声临界折射纵波(LCR波)对应力较为敏感,而LCR波主要是沿着被测物体表面、亚表面进行传播,因此这种方法不仅可用于表面残余应力的检测,也可以对物体亚表面的残余应力进行检测[14]。
根据相关理论和实验研究发现,沿应力方向传播临界折射纵波(LCR)在固定传播距离内(测量两点间距3 cm),被检测波速与被测物体内应力之间的关系推导出应力与声速的简化式[15]
Δσ=KΔt (1) 式中:K为声弹性常数,可通过拉伸实验标定获得;
Δσ=σ−σ0 ,σ 为被测试样残余应力,σ0 为标定试样残余应力,因为标定试样需进行热处理消除应力,σ0 接近为0;Δt=t−t0 ,t0 为零应力条件下LCR波传播固定距离所需要的时间,t 为LCR波沿被测试样内传播相同距离所需要的时间。根据式(1),可以通过精确测量LCR波在被测物体内传播的声时差,就可以计算得到对应的应力值。由式(1)还可看出,在被测物体内沿残余应力方向传播的LCR波传播所用时间的变化量与物体内的残余应力变化量成线性关系,所以根据声时的变化量就可以计算出对应的残余应力值。残余应力有拉应力和压应力,如果测量出残余应力值为正,表示物体内的残余应力为拉应力,如果测量出残余应力值为负,表示物体内的残余应力为压应力[14]。LCR波传播示意图如图1所示。
1.2.2 SLM残余应力神经网络模型
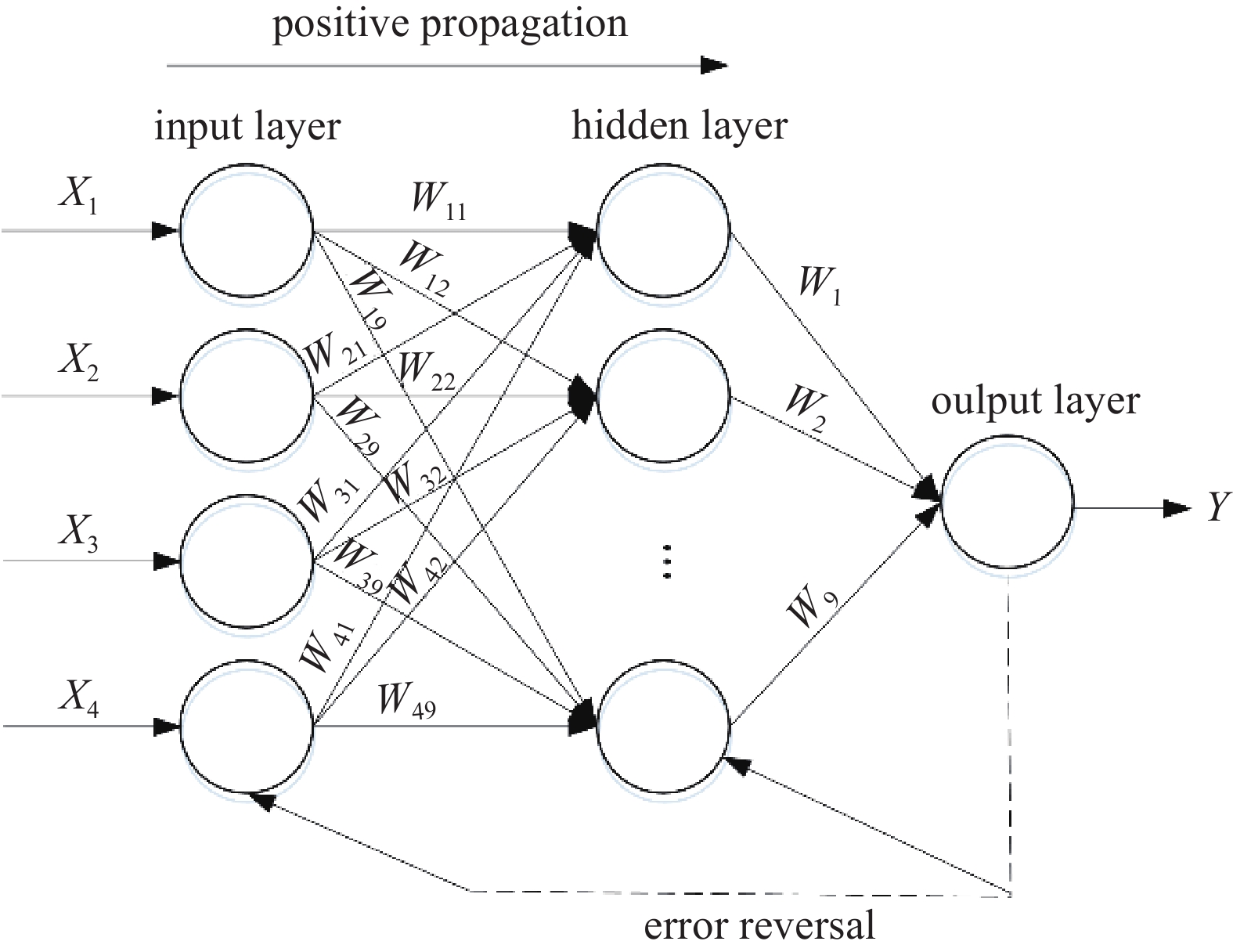
BP神经网络是一种按输出误差反向传播算法进行训练的自适应前馈神经网络,由输入层、隐含层和输出层组成,是目前该研究领域使用非常广泛、十分成熟的神经网络模型,该模型具有逼近能力强、训练算法成熟、计算量较小、并行性较强等优点[12-13,16]。
如图2所示,建立根据SLM工艺参数预测残余应力的BP神经网络模型。输入层有4个神经元:激光功率X1、扫描速度X2、铺粉层厚X3以及粉末预热温度X4,虽然扫描路径对残余应力也有较大影响,但由于扫描路径的量化还有待进一步研究,暂不作为输入参量。隐含层数量为1层,根据Kolmogorov定理[17-18]确定神经元个数=输入层节点数×2+1=9个;输出层有1个神经元:残余应力Y。这样整个BP神经网络结构为4×9×1三层结构。
1.2.3 实验步骤
首先采用AM400型号选区激光熔化系统制备试样,试样分两种:第一种为零应力标定试样A,如图3(a)所示;第二种为用于检测残余应力试样B,如图3(b)所示。
试样A制作3个,经热处理消除残余应力后,使用超声波检测仪测量传播一定距离所用平均时间
t0 ,用加载外部拉力使其内部产生拉应力,用超声波检仪器测量其传播固定距离声时,测出一组在弹性阶段加载不同的拉应力对应的声时,然后用数据拟合的方法计算出样本的声弹性常数K。试样B的参数设置如下:激光功率范围为50~400 W,激光扫描速度范围为0.25~1.5 m/s,铺粉厚度50,80 μm,基板预热温度50,100 ℃。由4种参数共设置188组不同组合的样本,用于模型构建的样本180个,具体参数设置如表2所示,另外有8个独立样本用于测试模型,为了减少实验误差,该实验中所有样本为同批次试样。由于激光功率和扫描速度参数级别较多,不适合采取全部正交方式,只将激光功率的100,200,300 W,扫描速度的0.25,0.5,0.75 m/s,铺粉厚度50,80 μm以及基板预热温度50,100 ℃几种设置为正交方式,共36个样本。试样实物照片如图4所示。
表 2 训练样本SLM工艺参数Table 2. Training process parameters of experiments in SLMprocess parameter laser power/W scanning speed/(m·s−1) powder thickness/μm preheating temperature/℃ level 1 50 0.25 50 50 level 2 100 0.375 80 100 level 3 150 0.5 − − level 4 200 0.625 − − level 5 250 0.75 − − level 6 300 0.875 − − level 7 350 1 − − level 8 400 1.125 − − level 9 − 1.25 − − level 10 − 1.5 − − 用超声波仪器对188个试样进行同距离测量超声传播所用时间
ti (第i个样本所用时间),得到Δt=ti−t0 。代入式(1)即可计算出所有样本的残余应力值。利用Matlab仿真软件构建合理的神经网络模型,对样本进行分类,训练集样本占70%,用于神经网络的训练。验证集样本占15%,测试集样本占15%,用于对模型进行验证和测试。
2. 实验结果及分析
2.1 微观结构分析
由于神经网络需要基于有效的样本进行训练,所建模型才能进行有效预测。因此需要对所选用试样进行遴选,剔除不合格的试样,而进行微观结构观测是挑选合格样品的一种基本方法。图5是试样B不同区域的微观结构图,从图中可以清晰看到柱状晶、等轴晶、胞状晶,以及熔池分界线。所选试样中无球化、欠熔合和气孔等对残余应力有较大干扰的缺陷,这类试样能够代表正常SLM工艺试样进行有效建模实验。
2.2 宏观测量结果分析
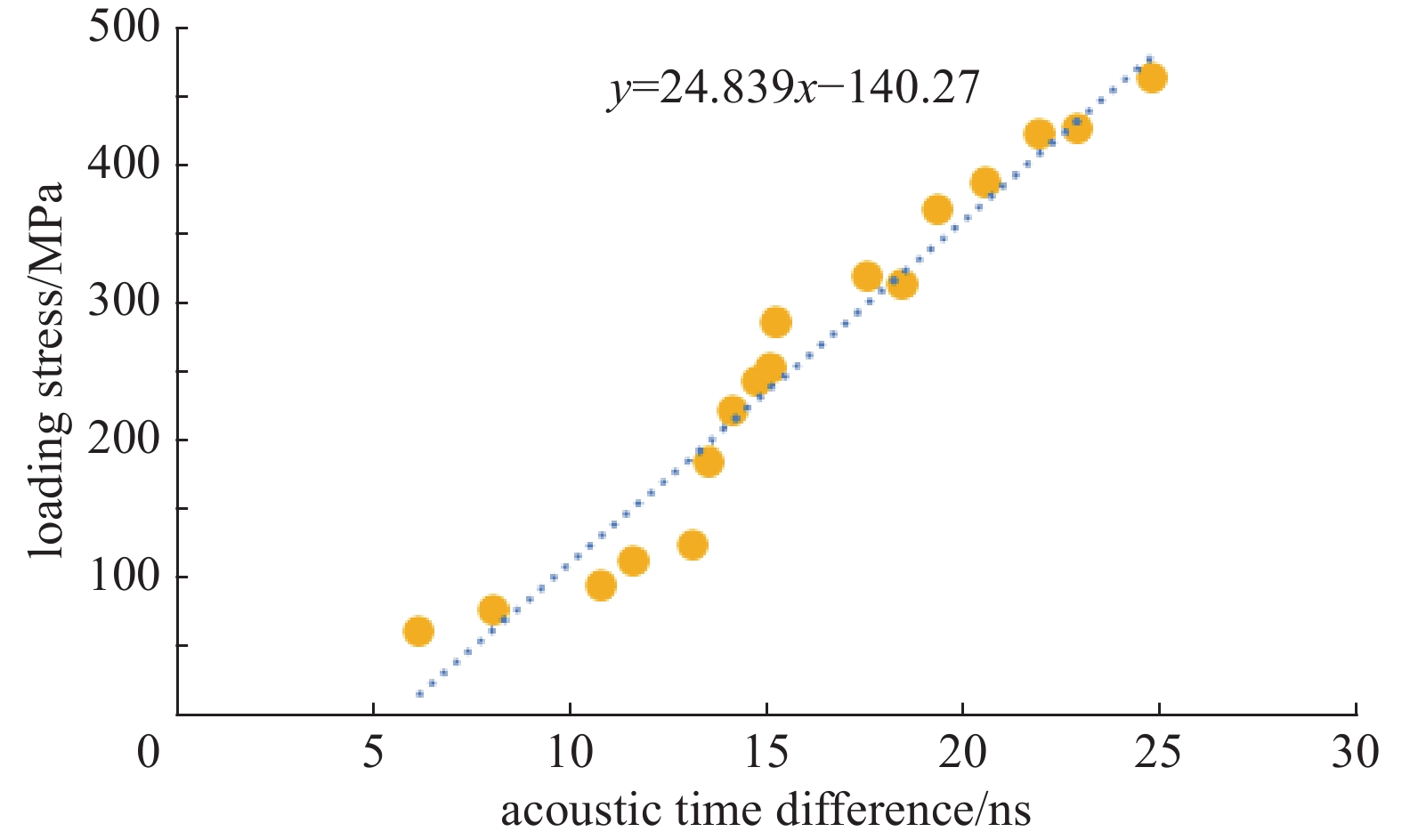
对3个试样A进行5次拉伸实验,对加载相应拉力的声时差取平均值,根据数据拟合出声时差-加载应力曲线如图6所示,求得K=24.839。
将试样A标定为零应力基准,测量188个试样B的声时差,并计算出测量两点间的平均残余应力,其中训练样本126个,验证样本27个,测试样本27个,独立测试样本8个。
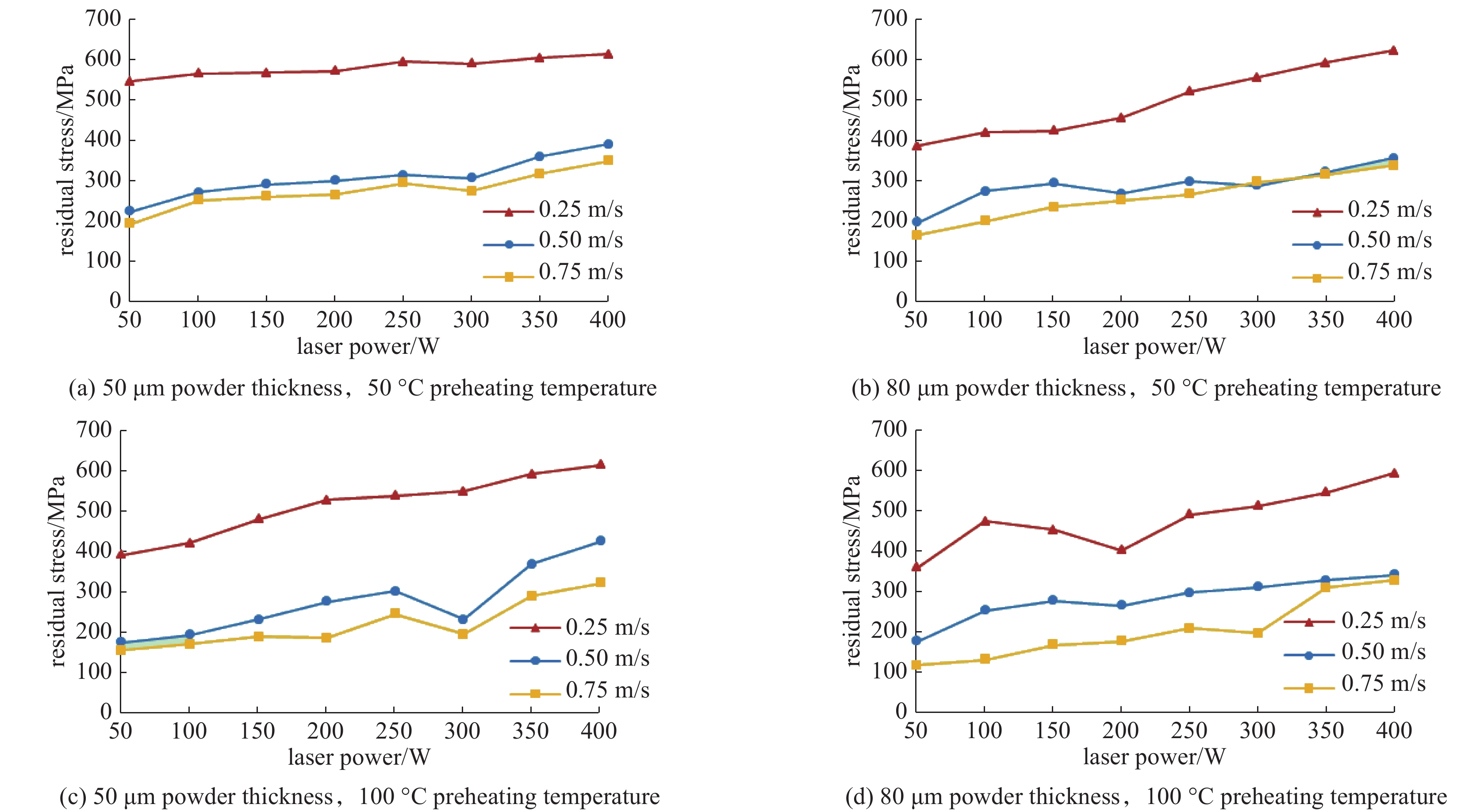
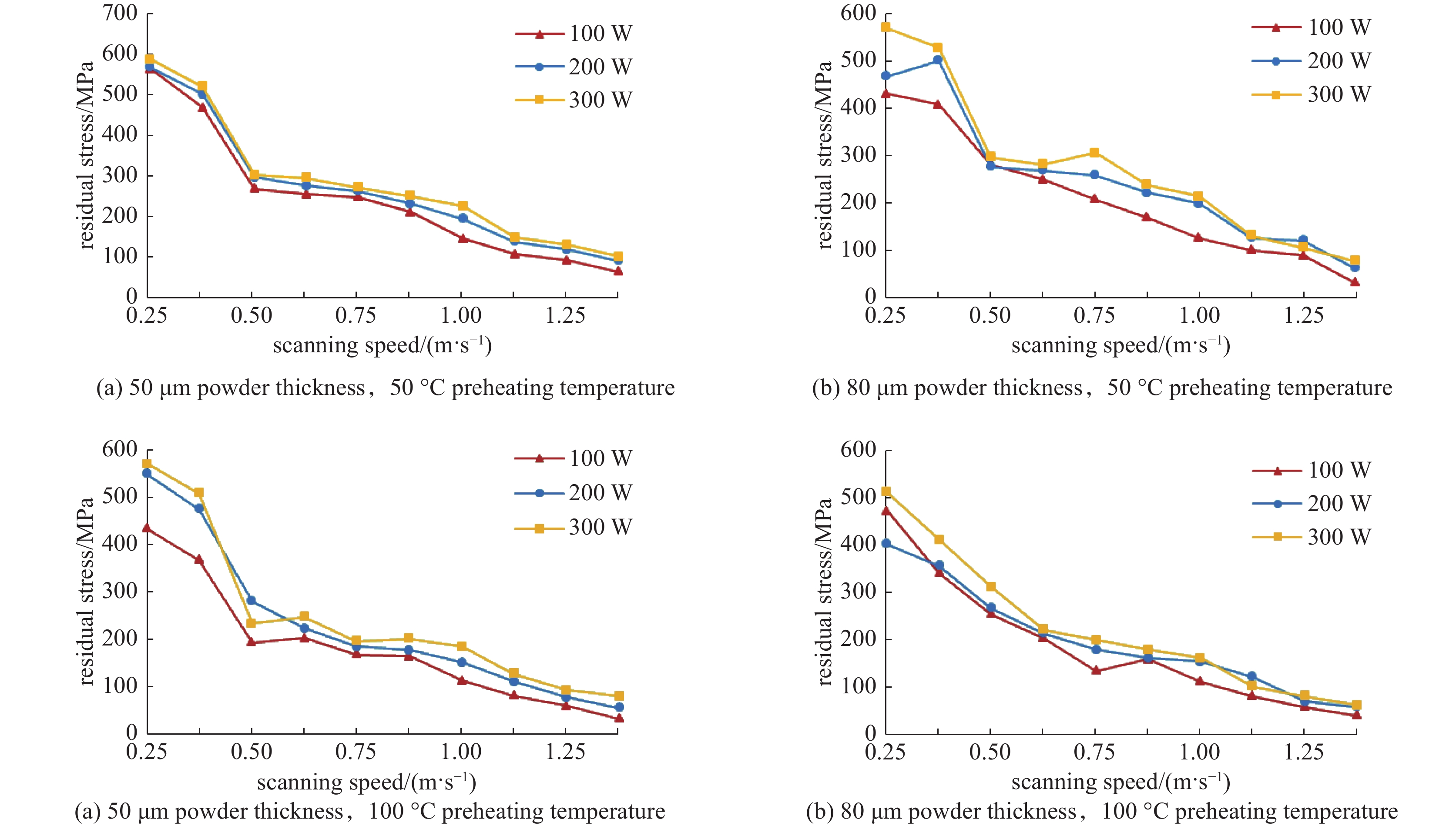
根据训练样本工艺参数及所测残余应力值,生成了残余应力随功率及扫描速度变化曲线。图7为功率-残余应力曲线,由图7可以看出,残余应力随着激光功率的增大总体呈上升趋势,而随扫描速度、铺粉厚度、基板预热温度增大而减小。图8为扫描速度-残余应力曲线,由图8可以看出,残余应力随着扫描速度的增加总体呈减少趋势,随功率增大而增大,随铺粉厚度和基板预热温度增加而减小。实验结果与文献[6-7]所述理论基本吻合。
2.3 神经网络模型残余应力预测结果分析
利用188个样本数据进行神经网络BP模型的训练、验证和测试,实验采用Matlab软件nftool工具箱进行,传递函数采用双曲正切S型,收敛误差设置为1×10−7。经过10次训练,模型均能在迭代5000次以内收敛,平均迭代次数为1108次,其中一次的迭代次数为1087次,权值和阈值为
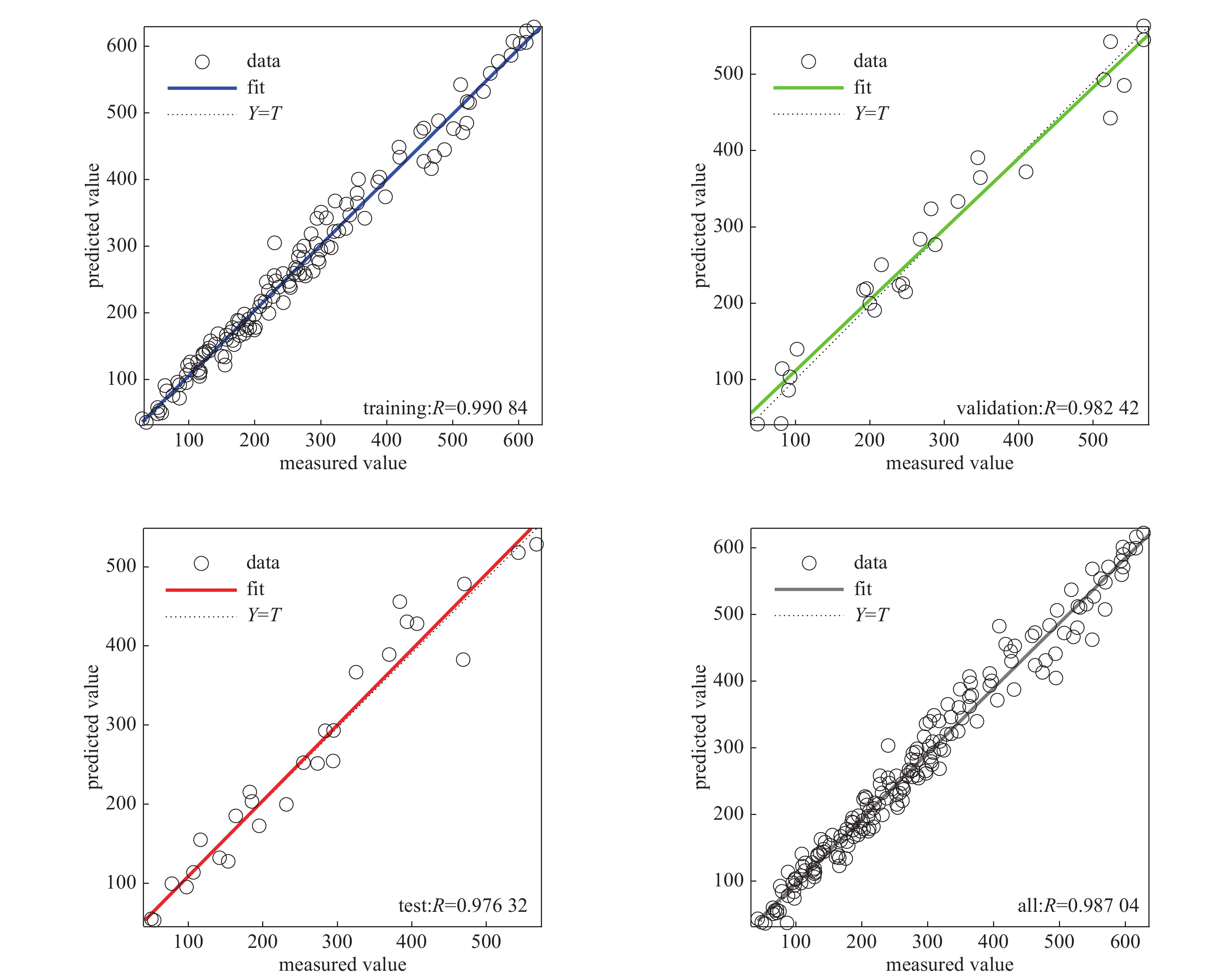
w1 =[0.0085 1.4333 0.0826 0.0495; −0.8120 −3.6343 0.0198 −0.1223; 0.4819 0.6551 −0.1803 −3.3366; −0.5859 −0.7200 0.2120 0.0336];θ1 =[−13.4804 −1.4298 3.0762 −0.7379]T;w2 =[1.0531 4.3820 −2.8806 −2.6033; 2.1871 1.2762 2.2849 −4.3661; 2.2429 −1.7579 2.0951 5.2451; 1.4588 0.8342 −1.4820 −1.4310; 0.2308 −3.1152 6.0000 1.5555; −2.8464 −1.1307 −2.8373 2.7147; 0.7400 −3.6950 1.3990 4.9451; 4.1972 −1.5955 −1.7148 −5.3371; −0.4752 −3.6304 −1.6067 −2.6885];θ2= [1.0374 −2.4766 −1.5273 0.0725 0.4017 0.6768 1.7951 −0.4645 3.6426]T。利用构建好的神经网络预测模型,对训练样本、验证样本和测试样本进行预测,预测值和实测值的线性回归分析如图9所示,回归模型拟合程度比较好,预测误差较小。
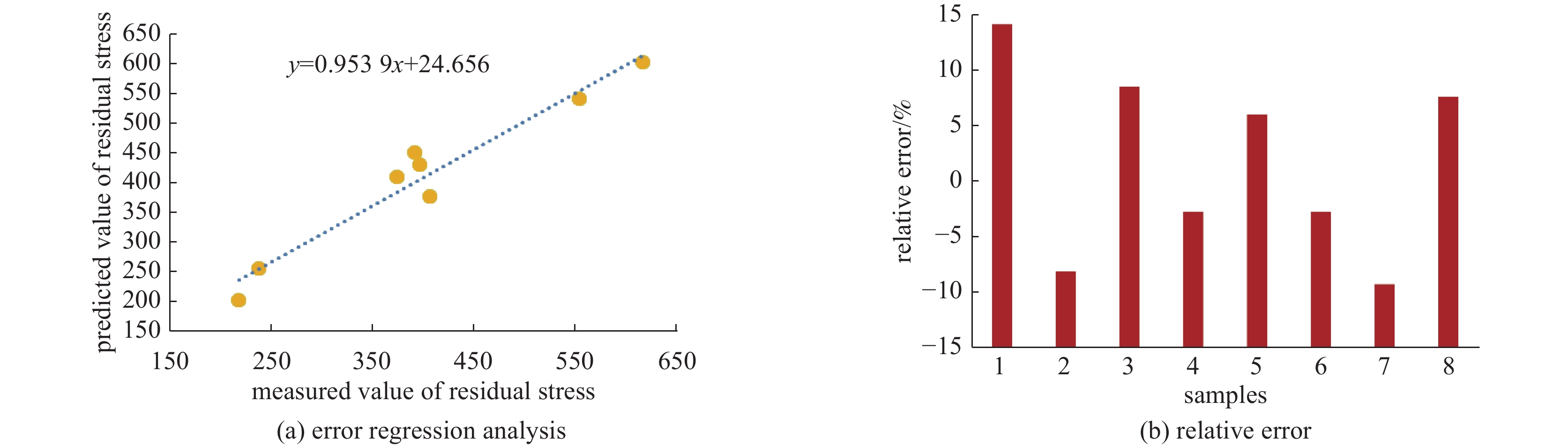
为了进一步验证预测模型的有效性,将8个独立验证样本输入训练好的模型进行预测,其预测值和实测值回归分析结果的拟合程度较高,如图10(a)所示,相对误差都在±15%以内,平均误差为7.34%,如图10(b)所示。姜淑娟等人[13]所做实验中超声波轴向应力检测平均误差在10%以内,徐春广等人[19]所做实验中当应力值为20 MPa时,相对误差小于25%,大于100 MPa时,相对误差小于5%。利用有限元数值模拟方法参考文献中,黄本生等人[20]所做实验平均误差为7.5%,于宝义等人[21]做实验平均误差为19%。由于本文所做实验并未考虑试样样本因在基板摆放位置产生的散热不同而产生的温度差异,训练样本数量还不够多,测量方法也存在一定误差,所以模型预测的准确度还有提升的空间。
3. 结 论
利用BP神经网络高度非线性函数进行逼近能力和自适应学习能力,构建了适合预测SLM工艺参数和残余应力的神经网络模型。根据超声临界折射纵波传播声时差与残余应力差的线性关系,检测出SLM试样训练样本的残余应力值,残余应力随工艺参数的变化趋势与理论分析大体一致:残余应力随激光功率增大而增大,随扫描速度、铺粉厚度、基板预热温度增大而减小。根据样本训练出的神经网络模型预测结果与残余应力变化趋势大体一致,总体预测效果较为理想。目前只采用了316L粉末进行实验验证了本文提出的方法,对于其他金属材料粉末是否适用还需要进一步实验研究。本文个别样本预测误差较大,还需要进行深入研究,优化实验环节,建立恒温恒湿环境,减少环境温度不一致造成的误差,考虑基板不同位置因热量扩散速度不一致导致温度的差异,找出温度场的变化规律,对基板预热温度做出修正,减少模型误差,提高预测准确度,并能在确定各种误差源的基础上,定量分析模型预测的准确度。
期刊类型引用(5)
1. 袁显宝,刘曾豪,张彬航,张永红,唐海波,杨森权,肖云龙. 基于BEAVRS基准题的三维堆芯建模计算及不同均匀化方案比较分析. 核技术. 2024(01): 108-118 .  百度学术
百度学术2. 沈芷睿,孙启政,何东豪,潘清泉,张滕飞,彭良辉,杨伟焱. 基于BEAVRS基准题高保真建模的OpenMC程序和NECP-X程序的对比验证. 核技术. 2022(01): 73-81 .  百度学术
百度学术3. 秦凯文,杨波,刘义保,张洁茹,郝鹏飞,刘豪杰. BEAVRS堆芯k_(eff)的敏感性与不确定性分析. 核技术. 2022(02): 71-77 .  百度学术
百度学术4. 郝鹏飞,杨波,秦凯文,张洁茹,刘义保. 基于BEAVRS基准例题的OpenMC程序建模及计算验证. 能源研究与管理. 2021(04): 80-84+95 .  百度学术
百度学术5. 张新营,刘滨,付鹏,盛洁. 电子加速器驱动次临界系统的靶物理设计及耦合计算. 核科学与工程. 2021(05): 1047-1054 .  百度学术
百度学术其他类型引用(5)
-

 点击查看大图
点击查看大图
计量
- 文章访问数: 1491
- HTML全文浏览量: 260
- PDF下载量: 823
- 被引次数: 10




 下载:
下载:
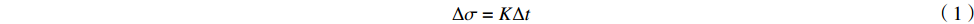
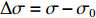
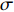
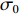
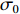
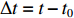
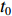
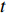



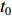

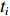
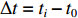




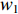
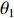


 下载:
下载: