Monte Carlo simulation of Cherenkov light generated by underwater Co-60 source
-
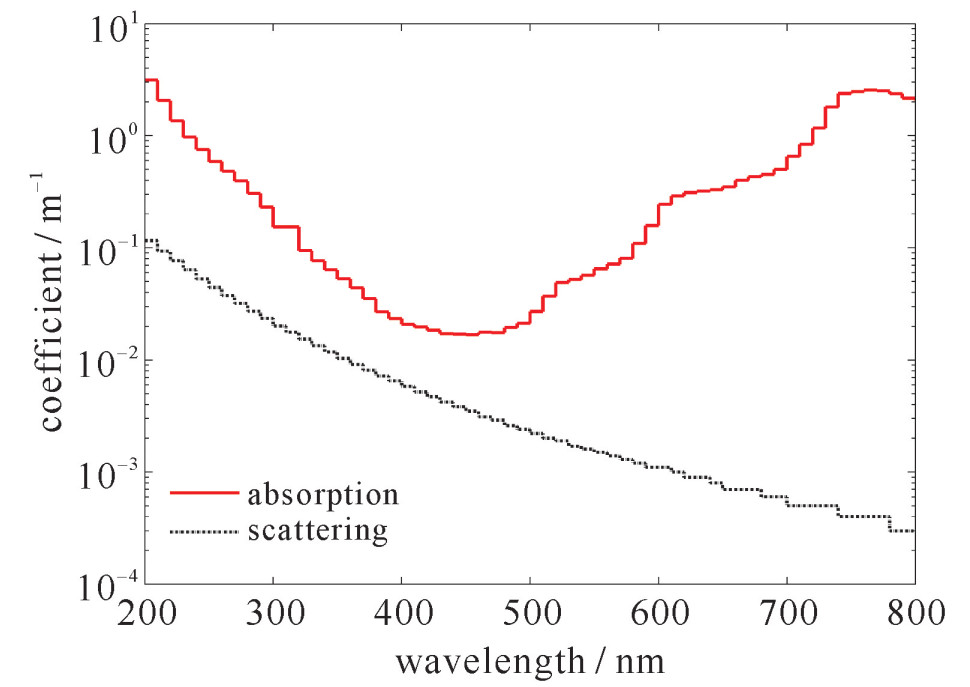
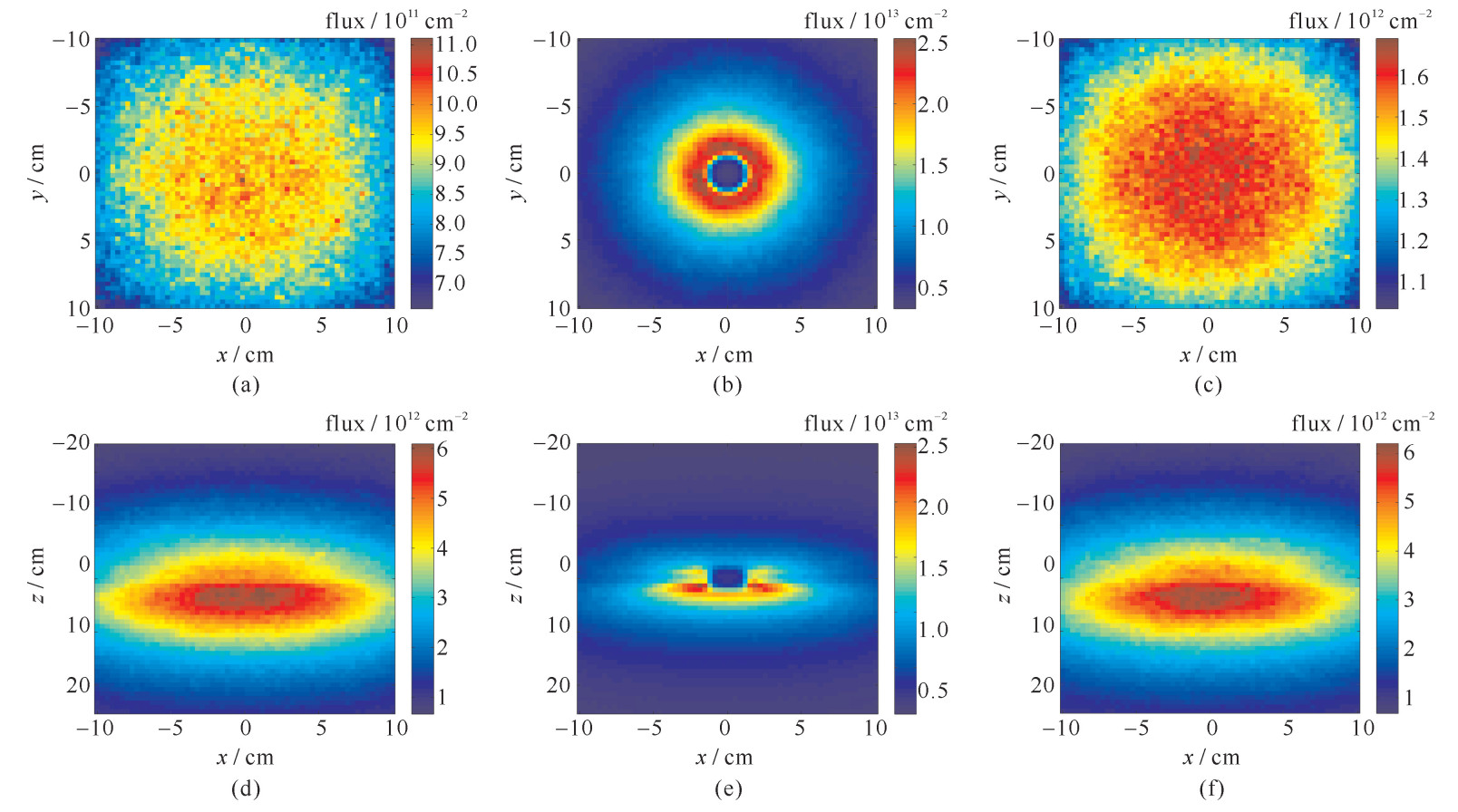
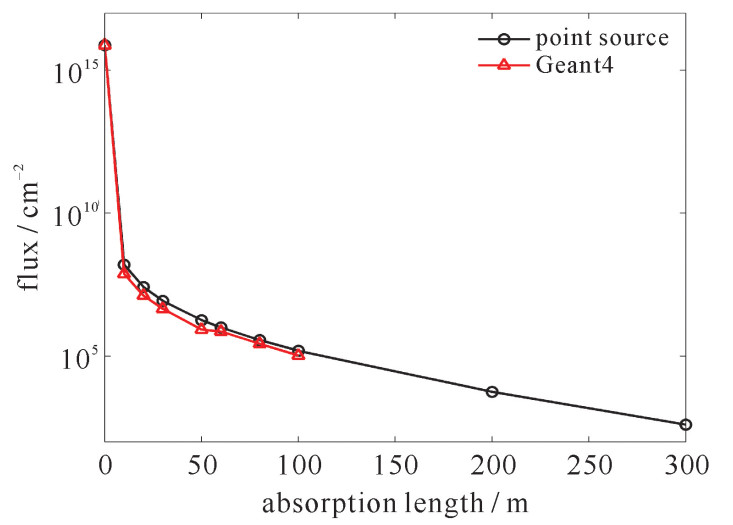
摘要: 随着核应用领域的不断拓宽,放射源丢失事故发生的概率也随之增加。机载伽马谱仪可有效搜寻地面放射源,然而对于放射源丢失于水域的情况,由于伽马射线经由水层屏蔽后可探测性降低,故利用放射源在水中产生的切伦科夫辐射对其进行搜寻显得十分重要。采用MCNP与Geant4相结合的方法,以及在Geant4程序中采用接续计算技巧,对Co-60源在水中的切伦科夫光产生以及传输进行了计算,计算表明,切伦科夫光经水中传播后,主要波段在300~600 nm,强度呈由边缘到中心渐强的特征分布,分布范围大致与放射源在水中的深度一致,在水中传输300 m后其光通量约为100 cm-2,可利用光谱特征和强度分布特征对其进行测量。
-
关键词:
- 放射源丢失 /
- 切伦科夫辐射 /
- MCNP耦合Geant4计算 /
- Geant4接续计算 /
- 光学测量
Abstract: With wide application of nuclear techniques, accidents of lost radioactive sources increase. The airborne gamma spectrometer can be used for searching the lost radiation sources on the ground level. However, for radioactive sources lost in water, the use of gamma spectrometer is limited as a result of the shielding of gamma rays by water. So detection of underwater radioactive source based on Cherenkov light generated by the radioactive source is becoming important. With applications of combined simulation of Geant4 and MCNP, and continuation simulation method in Geant4, distributions and transmission of Cherenkov light generated by underwater Co-60 sealed source were simulated. The simulation reveals that wavelength of Cherenkov light is between 300~600 nm through transmission in water. The light intensity becomes stronger from the edge to the center, and the distribution range approximately equals to the depth of the radioactive source in water. The light flux is about 100 Cherenkov photons·cm-2 after 300 m transmission in water. The Cherenkov light can be detected by the characteristics of its wavelength spectrum and intensity distribution. -
High-resolution flow field data play an important role in fluid mechanics, fluid dynamics research, engineering design and technological innovations. Accurate acquisition and analysis of high-resolution flow field data is of great significance for understanding flow phenomena. There are two main ways to obtain high-resolution flow field data, one is experimental measurements, such as Particle Image Velocimetry (PIV)[1], the other is Computational Fluid Dynamics (CFD)[2], such as Direct Numerical Simulation (DNS)[3-5]. However, obtaining high-resolution flow field data through experiments or CFD is either costly or time-consuming, thus new methods need to be developed.
Artificial intelligence technology has been booming unprecedentedly nowadays[6]. As the main method of artificial intelligence, Convolutional Neural Networks (CNN)[7] has been widely used in various fields and promoted many innovations and progress. CNN is a deep learning model inspired by the biological vision system. The development of CNN has experienced many milestones. The earliest CNN model can be traced back to the 1990s, such as LeNet[8] proposed by LeCun for handwritten digit recognition. In the 2012 ImageNet Large-Scale Visual Recognition Challenge, the emergence of the AlexNet[9] model has greatly promoted the development of CNN, which uses a deeper networks structure and a large amount of image data for training, and achieved breakthrough results. Since then, various improved CNN models have emerged, such as VGGNet[10], GoogLeNet[11], ResNet[12], etc., which have achieved excellent performance in different computer vision tasks.
The vigorous development of CNN has been spread to various fields, including fluid mechanics. Especially in recent years, fluid mechanics has been closely combined with CNN. In 2018, Jin et al designed a fused CNN model[13]. Through this model, the velocity field around the cylinder can be predicted only according to the pressure fluctuation on the cylinder. This model has good performance under different Reynolds numbers. In 2019, Sekar et al first used CNN to extract the geometric features of the airfoil[14], and to predict the flow field around the airfoil through the fully connected layer with the help of other state information. In the direction of high-resolution reconstruction of the flow field, Fukaimi et al proposed a hybrid Down sampled Skip-Connection Multi-Scale model to reconstruct the flow field[15] in 2019. In this model, only dozens of training samples are used to produce a good performance. At the same year, Deng et al constructed two models based on generative adversarial networks to enhance the spatial resolution of the complex wake behind two side-by-side cylinders[16]. In 2020, Liu et al developed the multi-time-path CNN model for high-resolution reconstruction of turbulence[17]. In 2021, Zhou et al used the geometric parameters of the coarse velocity field and the pore structure as the input of the CNN model to achieve super-resolution reconstruction of the pore flow field in porous media[18]. In 2022, Jagodinski et al designed a three-dimensional CNN model to identify significant structures related to ejection events in wall-bounded turbulent flows[19].
The ablative Rayleigh–Taylor instability (ARTI)[20] flow field data is mainly obtained by numerical simulations and experiments. At present, high-precision simulation requires fine meshing, however, it is costly and time-consuming. Low-precision simulation takes a short time, but it cannot describe the physical characteristics of the flow field in detail. Therefore, we need to develop a new method that can obtain high-precision ablation Rayleigh-Taylor instability flow field data at a relatively small computational cost. In this study, two different CNN models are given out to perform the high-resolution reconstruction. These two models can quickly transform low-resolution data into high-resolution data, which allows us to obtain high-resolution ARTI flow field data rapidly.
1. Methods
1.1 ARTI and DNS
The Rayleigh–Taylor instability (RTI) occurs at the perturbation interface of two fluids with different densities, where the light fluid accelerates or supports the heavy fluid[21]. In inertial confinement fusion (ICF), RTI can break the symmetry of implosions by dismantling the integrity of the spherical ablator-fuel shell. Therefore, it is crucial to predict the growth of RTI to improve the success probability of ICF. The inclusion of thermal conduction influences leads to a different hydrodynamic instability, which is then identified as ARTI, occurring between the internal and external layers during the implosion phase of ICF[22].
The control equations of the ARTI over a constantly accelerating 2D reference frame are as follows
∂tρ=−∂x(ρu)−∂y(ρv), (1) ∂t(ρu)=−∂x(ρu2+p)−∂y(ρuv)+ρg, (2) ∂t(ρv)=−∂x(ρuv)−∂y(ρv2+p), (3) ∂t(ρe)=−∂x[(ρe+p)u]−∂y[(ρe+p)v]+∂x(κ∂xT)+∂y(κ∂yT)+ρug, (4) where
ρ , u, v and T represent density, x-axis velocity component, y-axis velocity component and temperature, respectively. g is acceleration,p=ΓρT is the pressure, ande=CvρT+ρv22 is the total energy, whereCv=Γ/(γh−1) is the constant-volume specific heat. For CH material,γh=5/3 andΓ=57.51cm2/(μs2⋅MK) .κ=κSHf(T)h is the coefficient of thermal conductivity, whereκSH∝T5/2 is the classical electron thermal conductivity coefficient.f(T)=1+bT+c/T3/2 is the preheating function, andh=1/[1+B⋅ln(TmaxT0)] because there is a large temperature gradient near the critical surface,T0 andTmax are the initial electron temperature and the maximum electron temperature, respectively, in the corona region, and B is an adjustable parameter, usuallyB=1 . For the strong preheat case discussed in this paper, we set h=1, b=8.6, c=1.6.The data used in this work are derived from the DNS of ARTI in Ref.[4], and the Euler code which has been usually applicated in high energy density physics is used in our study. Before the formal training of the CNN model, we process the original DNS data through region selection, dislocation stitching, pooling and other processes to obtain the sample data. In this paper, both maximum pooling and average pooling are used to implement down-sampling.
1.2 Two CNN models
In this paper, the application of ordinary CNN model and multi-time-path CNN model are discussed, and the results are also compared with those of the BiCubic interpolation method[23].
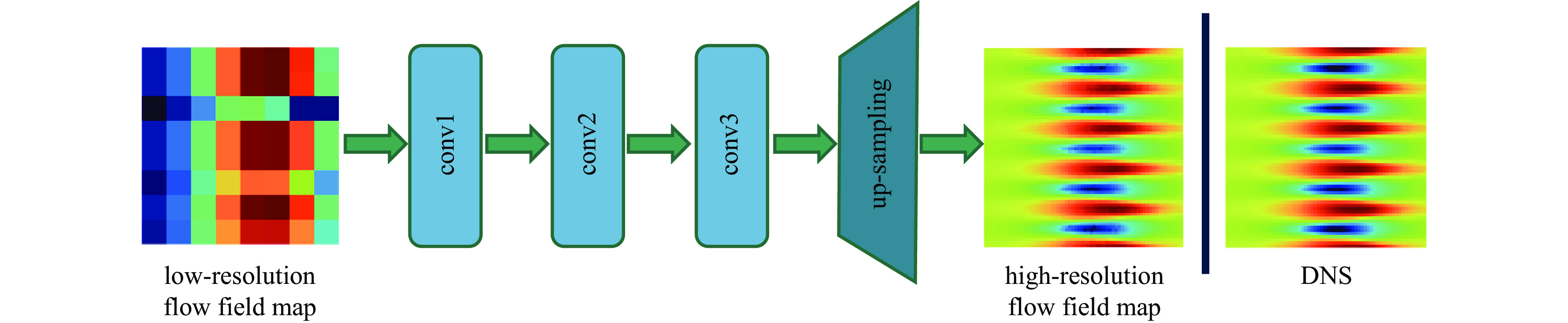
The ordinary CNN model consists of three convolution layers and an up-sampling layer, as shown in Fig.1. The input of the model is the low-resolution flow field data and the output is the high-resolution flow field data at the same time. The role of the convolution layer is to extract the characteristics of the flow field data. The size of the convolution kernel is
3×3 . The function of the up-sampling layer is to integrate and enlarge the feature maps obtained by convolution operation, so as to achieve high-resolution reconstruction. The PixelShuffle up-sampling method[24] is adopted to transform the feature map with the input size of(r2×C,H,W) into the flow field map with the input size of(C,r×H,r×W) by pixel recombination of the low-resolution feature map,where r is the reconstruction magnification, C is the number of channels, H is the height of the feature map, W is the width of the feature map.The second model is a multi-time-path CNN. The schematic diagram of the model is shown in Fig.2.
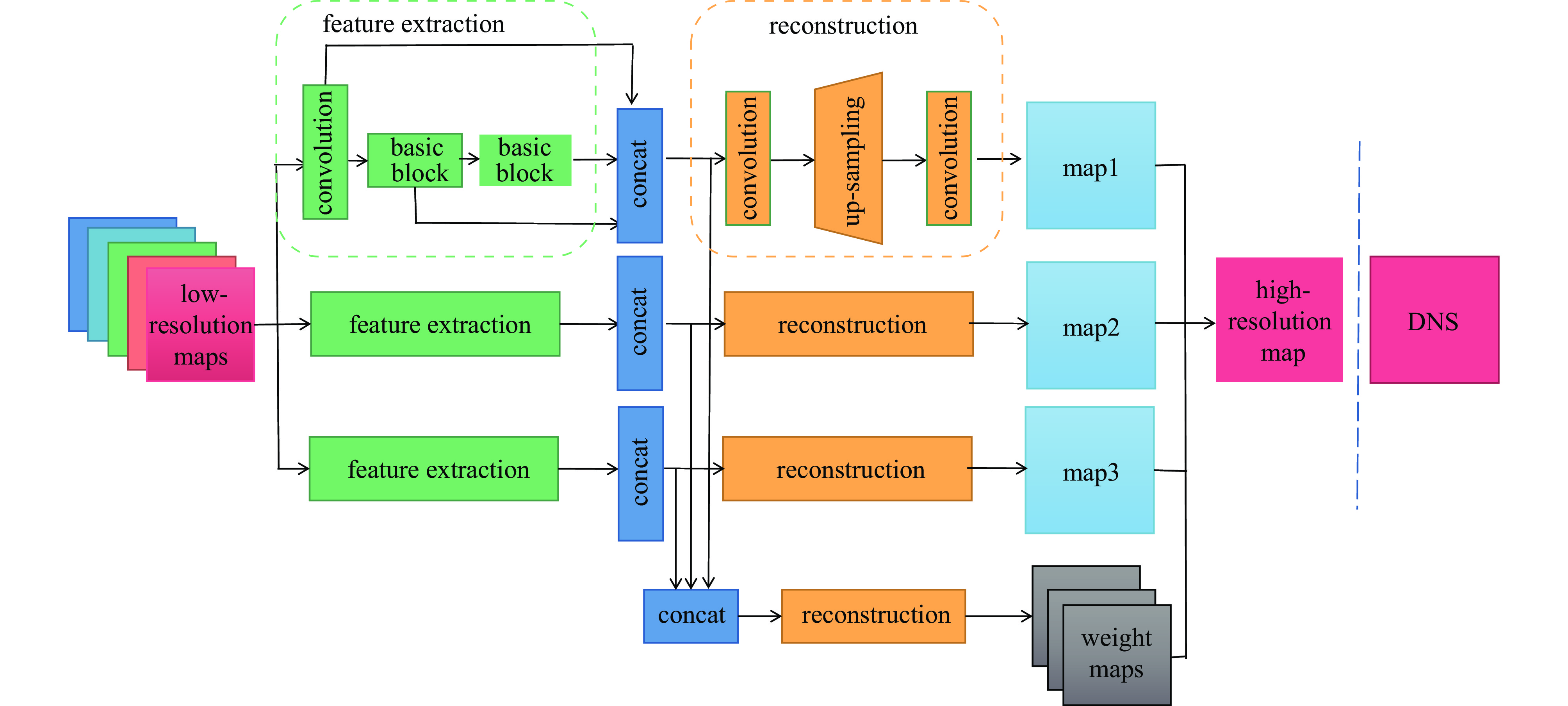
The input of the multi-time-path CNN is the low-resolution flow field data of the five moments at
t−2Δt ,t−Δt , t,t+Δt ,t+2Δt respectively and the output is the high-resolution flow field data of the moment t. The model includes four paths, three of which are time paths and the other is the weight path. The time paths include the backward time path, central time path and forward time path. The input of each time path is the low-resolution flow field data at three consecutive moments. The input of the backward time path is the flow field data at three moments oft−2Δt ,t−Δt , t. The input of the central time path is the flow field data at three moments oft−Δt , t,t+Δt . The input of the forward time path is the flow field data at three moments of t,t+Δt ,t+2Δt . Therefore, a set of input data of the model contains low-resolution flow field data at five moments. The structures of all the time paths are the same, including feature extraction module and reconstruction module. The feature extraction module consists of two basic blocks, each of which is an enhanced multi-scale residual block[25], and a jump connection method is used on each time path to avoid the loss of features caused by convolution operations. In the weight path, the input is the feature maps extracted by the feature extraction module of the three time paths, and the output is three weight maps. The summation of the products of the obtained weight map and the reconstructed flow field map obtained by the three time paths will finally give the high-resolution flow field map at the moment t. In other words, the final high-resolution flow field data is actually the weighted average of the high-resolution flow field data obtained by the three time paths.Compared with the ordinary CNN, multi-time-path CNN has more input data and more complex networks structure, thus the expected results should also be better than those of the ordinary CNN. It is worth mentioning that the multi-time-path CNN takes the time series as the model input, combines the timing of the flow field changing with time, and has the superiority that the ordinary CNN cannot achieve.
1.3 Model training
After a series of data processing, we randomly divided
2000 samples into 80% training set (1600 samples) and 20% test set (400 samples). Taking a magnification of 4 as an example, the input size of our ordinary CNN model is [C, 16, 16], and the input size of the multi-time-path CNN is [3, C * 3, 16, 16]. Because the multi-time-path CNN has three paths, there is an additional dimension on the input scale. Each path of the multi-time-path CNN contains data of three moments, thus, the number of channels is C * 3. The last two dimensions represent the height and width of the feature map. We set the batch size to be 32 and Epoch to be 2000.Before putting into training, the input data should be normalized, which will make the model converge faster. We select activation function as the ReLU function, which is often used in neural networks. Because our super-resolution reconstruction task is actually a regression task, we cannot use the activation function in the last convolution layer. For weight initialization, we also use the corresponding initialization method of ReLU function.
The loss function in the above two models is written as
L=∑Ni=1(Hi−Pi)2N, (5) where L is also called as Mean Square Error (MSE), N is the number of data point, H, P are the real value and the predicted value of the point, respectively.
All the models in this paper are in Python, which mainly depends on PyTorch to realize the construction of CNN model. As for gradient update, Adam[26] (Adaptive Moment Estimation) optimization algorithm is used to adaptively adjust the parameters in the neural networks, which can converge to the optimal solution quickly. In the parameter setting of Adam, we choose the learning rate 0.0001. The training process of the model involves iterating through 2000 epochs. The ordinary CNN takes 4 h and 2 min, and the multi-time-path CNN takes 4 h and 23 min. The structure of the multi-time-path CNN is more complex and has more parameters than the ordinary CNN, thus requiring a slightly longer computation time. After the model training is completed, the high-resolution reconstruction task can be achieved in a few seconds.
2. Results and analysis
The DNS data used here are ARTI flow field data with a disturbance wavelength
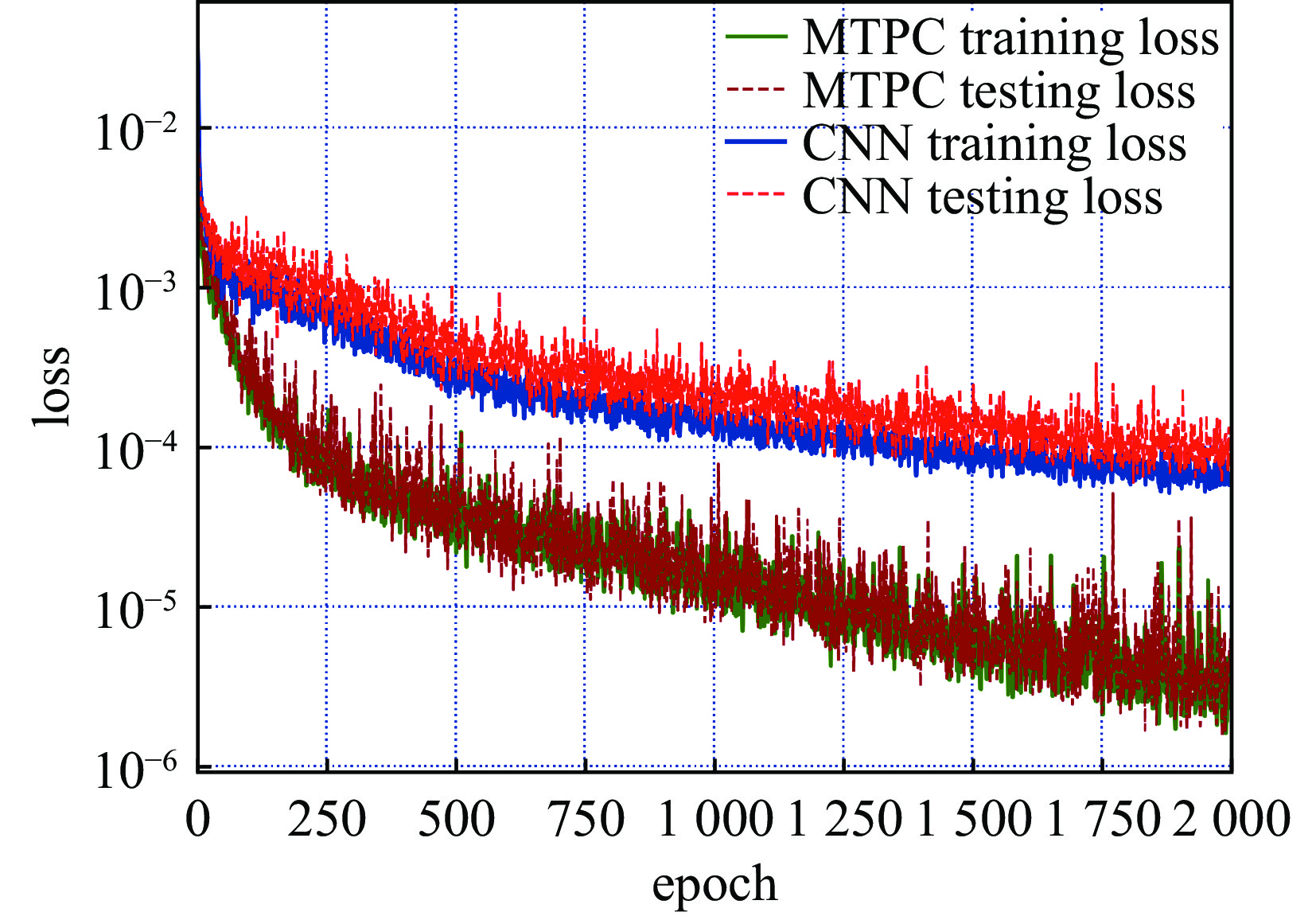
Ld=12μm . Firstly, the velocity field is reconstructed by using the data of the two channels in the x, y directions as the input of the model. The training error and test set error of the ordinary CNN model and the multiple CNN model are shown in Fig.3.In Fig.3, CNN represents the ordinary CNN, MTPC represents the multi-time-path CNN, training loss refers to the training set error, and testing loss refers to the test set error. Compared with the ordinary CNN, the error of the multi-time-path CNN is smaller, reduced by nearly 10 times. It can be said that the multi-time-path CNN has better reconstruction performance than the ordinary CNN.
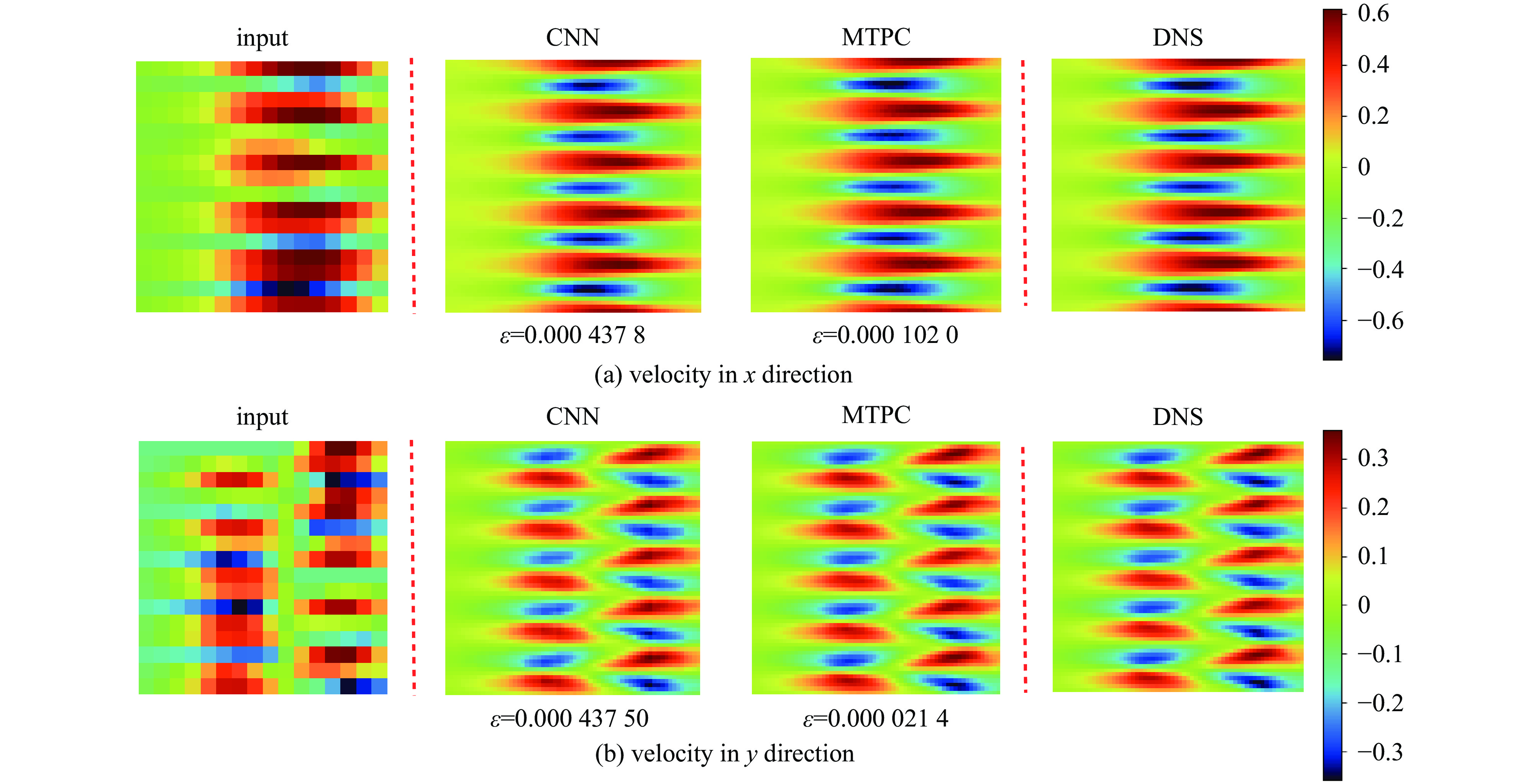
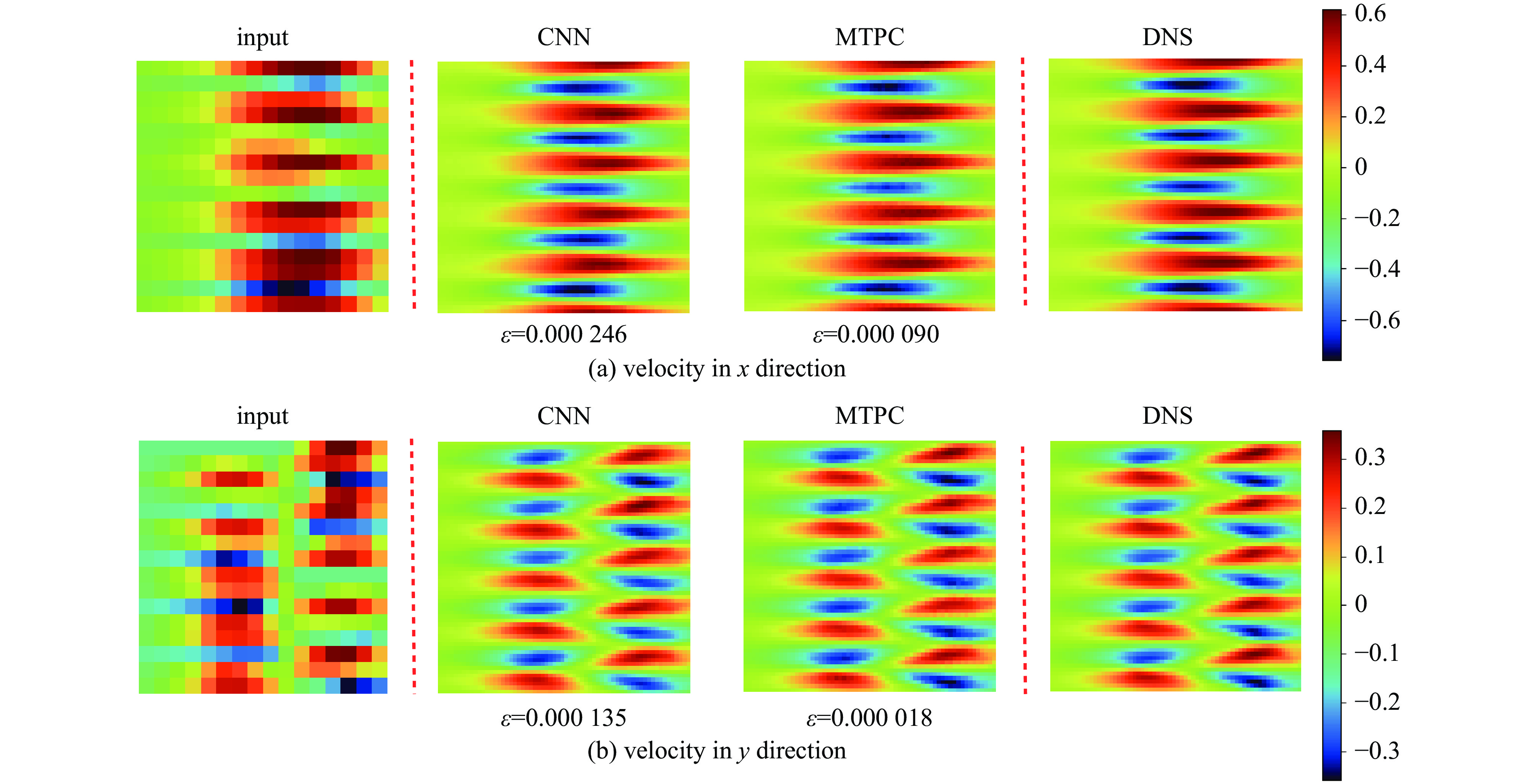
To more clearly show the superiority of the multi-time-path CNN, we compare the reconstructed results of the two models. All the data shown in Fig.4 and Fig.5 come from the same flow field,which are the flow field velocity data of the same position at the same time.
Fig.4 is the comparison of the reconstruction results when the input is the flow field velocity data in x and y directions after average pooling. Fig.5 is the comparison of the reconstruction results when the input is the flow field velocity data in two directions after maximum pooling. The reconstruction magnification r of the two figures is 4, and the
ε in the figure is the MSE. It can be clearly seen that the MSE of the multi-time-path CNN is much smaller than that of the ordinary CNN for both the average pooling case and the maximum pooling case. To show that the performance of the multi-time-path CNN is better than that of the ordinary CNN, we also compare the reconstruction results of models with magnification r= 8. The results show that even when the magnification r is 8, the error of the multi-time-path CNN is still much smaller than that of the ordinary CNN. Compared with the case of magnification r being 4, the error increases when the magnification r is 8, which is also in line with expectations: as the magnification increases, the amount of input data decreases, and the error of the model should also increase. Comparing the results of average pooling and maximum pooling, average pooling will lead to smooth prediction results but reduce accuracy, while maximum pooling can retain more details and help to improve prediction accuracy, but the results are not as smooth as average pooling.Furthermore, the density of the flow field is also used for training the model as a separate input. To demonstrate the universality of the model, we analyze the flow field density data of four cases (r=4). The first case is the density data of the weak nonlinear stage with ablation (disturbance wavelength=12 μm), as shown in Fig.6.
BiCubic in Fig.6 denotes the results of the BiCubic interpolation reconstruction method, and the BiCubic interpolation method is widely used in image processing. The prediction results of the BiCubic interpolation method exhibit excessive smoothness, resulting in the loss of numerous detailed characteristics within the flow field. It can be clearly seen from Fig.6 that the performance of both ordinary CNN and multi-time-path CNN in high-resolution reconstruction of flow field data is far superior to that of BiCubic interpolation method. The multi-time-path CNN consistently demonstrates superior performance compared to the ordinary CNN, effectively recovering more flow field details with a lower error.
Fig.7 is the classical linear flow field density data (disturbance wavelength=12 μm), and Fig.8 is the density data of the nonlinear stage with ablation (disturbance wavelength=12 μm). In addition, we also discuss the flow field with the disturbance wavelength of 30 μm, as shown in Fig.9.
In these cases, the prediction error of the multi-time-path CNN is generally at the order of 10−5, while the error of the ordinary CNN is at the order of 10−4. Both of these errors are significantly lower than that of the the BiCubic interpolation method. It is shown by these cases that the multi-time-path CNN still exhibits excellent performance in the face of different flow parameters, different stages and different flow field data.
For the velocity component input case and the density component input case, the error of reconstructing the flow field based on multi-time-path CNN is low enough, and the performance is sufficiently good. This also fully demonstrates the feasibility of combining machine learning with fluid mechanics. The methods used in this paper can also be applied to other flow field data. Given a sufficient amount of flow field data, a corresponding high-resolution reconstruction model can be trained.
3. Conclusion
We have built an ordinary CNN and a multi-time-path CNN to achieve high-resolution reconstruction of the low-resolution ablation Rayleigh-Taylor instability flow field. Compared with the ordinary CNN, the multi-time-path CNN shows better performance and smaller error. In terms of the acquisition of input data, we first pooled the existing high-precision DNS data of our research group to obtain low-resolution flow field data, and then we performed dislocation splicing on the data to obtain training sample data. The influence of input data obtained by two pooling methods on model training is compared. The prediction results of the average pooling model are smoother, and the accuracy of the maximum pooling model is slightly higher. Different cases are discussed in this paper, and it is found that the multi-time-path CNN model still maintains excellent performance in different flow fields. Once the CNN model is trained, the high-resolution reconstruction task can be completed in just a few seconds. The introduction of these two models has enriched the application of CNN in fluid instability. With the development of computer technology, the training speed of CNN model will be faster and faster. We can construct more complex models to make the reconstruction accuracy higher and higher.
-
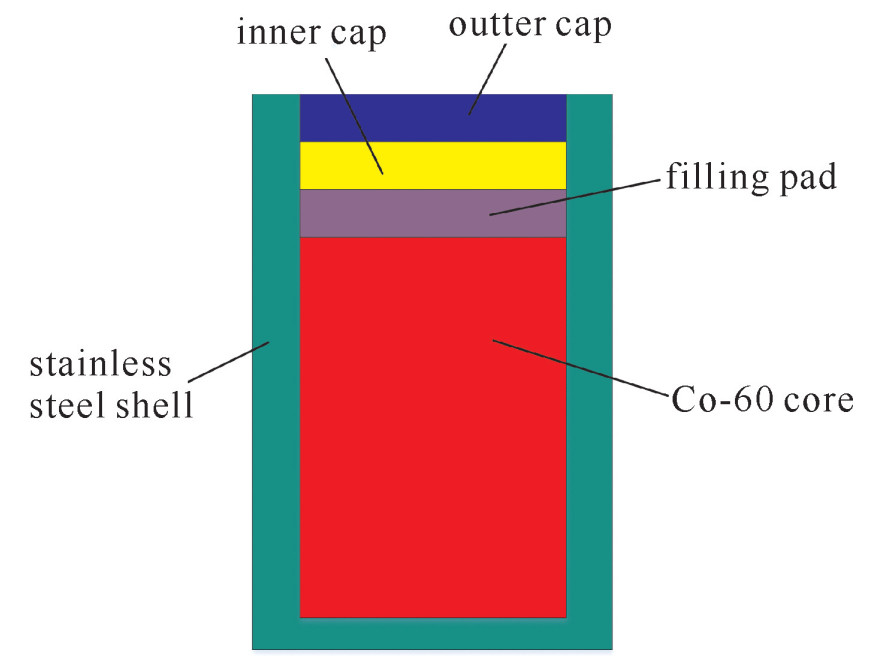
表 1 Co-60外壳表面伽马、电子源强
Table 1. Source intensity of gamma radiation and electrons
position gamma radiation
/(particles·s-1)electrons
/(particles·s-1)tube surface 1.358 4×1014 1.116 1×1012 top surface 6.822 4×1012 5.741 7×1010 bottom surface 2.126 1×1013 1.748 1×1011 -
[1] 闻良生, 龚频, 黄茜, 等. 小型旋翼机机载辐射环境监测系统的设计与实现[J]. 强激光与粒子束, 2016, 28: 106004. doi: 10.11884/HPLPB201628.160036Wen Liangsheng, Gong Pin, Huang Xi, et al. Design and implementation of minitype rotorcraft airborne radiation monitoring system. High Power Laser and Particle Beams, 2016, 28: 106004 doi: 10.11884/HPLPB201628.160036 [2] 倪卫冲, 刘士凯, 高国林, 等. AGS-863航空伽马能谱勘查系统机载试验[J]. 中国核科学技术进展报告, 2011, 2(1): 335-343. https://cpfd.cnki.com.cn/Article/CPFDTOTAL-EGVD201110001060.htmNi Weichong, Liu Shikai, Gao Guolin, et al. Airborne testing of AGS-863 airborne gamma spectrometry survey system. Progress Report on China Nuclear Science & Technology, 2011, 2(1): 335-343 https://cpfd.cnki.com.cn/Article/CPFDTOTAL-EGVD201110001060.htm [3] 翁渝民. 单光子计数-弱信号检测的有力手段[J]. 物理, 1980, 9(1): 20-24. https://www.cnki.com.cn/Article/CJFDTOTAL-WLZZ198001007.htmWeng Yumin. Single photon counting-efficient technique for weak single measurement. Physics, 1980, 9(1): 20-24 https://www.cnki.com.cn/Article/CJFDTOTAL-WLZZ198001007.htm [4] 舒迪昀, 汤晓兵, 侯笑笑, 等. 基于Cerenkov效应水下放射源搜寻技术的可行性分析研究[J]. 原子能科学技术, 2015, 49(4): 582-588. https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201504002.htmShu Diyun, Tang Xiaobing, Hou Xiaoxiao, et al. Analysis of feasibility for searching underwater radioactive source using Cerenkov effect. Atomic Energy Science and Technology, 2015, 49(4): 582-588 https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS201504002.htm [5] 刘斌, 贾清刚, 张天奎, 等. 水下切伦科夫光光斑的蒙特卡罗模拟[J]. 强激光与粒子束, 2013, 25(1): 196-200. doi: 10.3788/HPLPB20132501.0196Liu Bin, Jia Qinggang, Zhang Tiankui, et al. Monte Carlo simulation of Cherenkov light spot produced by underwater radioactive source. High Power Laser and Particle Beams, 2013, 25(1): 196-200 doi: 10.3788/HPLPB20132501.0196 [6] Agostinelli S, Allison J, Amako K, et al. Geant4—a simulation toolkit[J]. Nuclear Instruments and Methods in Physics Research A, 2007, 506(3): 250-303. https://www.sciencedirect.com/science/article/pii/S0168900203013688 [7] Allison J, Amako K, Apostolaki J, et al. Geant4 developments and applications[J]. IEEE Trans Nuclear Science, 2006, 53(1): 270-278. https://ieeexplore.ieee.org/document/1610988/ [8] Zhang Qingmin, Hu Zhigang, Deng Bangjie, et al. A simple iterative method for compensating response delay of self-powered neutron detector[J]. Nuclear Science and Engineering, 2017, 186(1): 293-302. [9] GB7465-2009. 高活度钴60密封放射源[S]. 中华人民共和国国家标准, 2009.GB7465-2009. High activity cobalt-60 sealed radioactive sources. PRC standard, 2009 [10] Pope R M, Fry E S. Absorption spectrum(380~700 nm) of pure water. Integrating cavity measurement[J]. Appl Opt, 1997, 36(33): 8710-8723. https://pubmed.ncbi.nlm.nih.gov/18264420/ [11] Quickenden T I, Irvin J A. The ultraviolet absorption spectrum of liquid water[J]. J Chem Phys, 1980, 72(8);4416-4428. [12] 曹婷婷, 罗时荣. 天空直射光谱和天空光谱的测量与分析[J]. 物理学报, 2006, 56(9): 5554-5557. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200709095.htmCao Tingting, Luo Shirong. Measurement and analysis of direct sunlight and skylight spectra. Acta Phsica Sinica, 2006, 56(9): 5554-5557 https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB200709095.htm [13] 徐英莹, 金伟其. 夜晚天空光谱辐射测量研究及光谱去噪分析[J]. 光谱学与光谱分析, 2012, 32(6): 1456-1459. https://www.cnki.com.cn/Article/CJFDTOTAL-GUAN201206006.htmXu Yingying, Jin Weiqi. Measurement of night sky spectral radiation and analysis of spectral denoising. Spectroscopy and Spectral Analysis, 2012, 32(6): 1456-1459 https://www.cnki.com.cn/Article/CJFDTOTAL-GUAN201206006.htm -





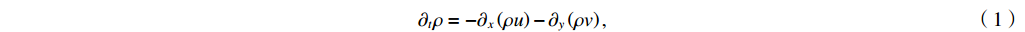
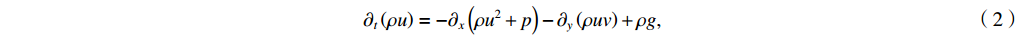
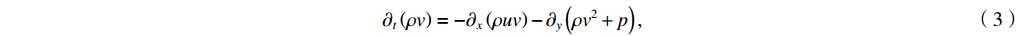
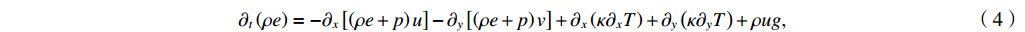
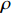
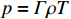
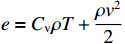
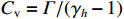
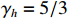
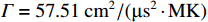
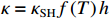
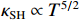
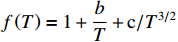
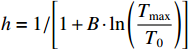
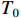
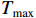
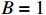

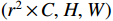
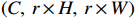

 DownLoad:
DownLoad:

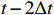
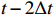
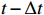
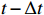
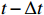


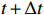
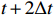
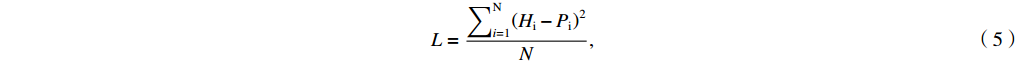
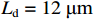



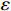




 下载:
下载: