求解中子动力学方程的加权蒙特卡罗方法

李捷; 李云召; 吴宏春; 郑琪

doi:10.11884/HPLPB201830.170242

求解中子动力学方程的加权蒙特卡罗方法

doi: 10.11884/HPLPB201830.170242

西安交通大学能源与动力工程学院, 西安 710049

基金项目:

国家自然科学基金项目 11522544

详细信息

作者简介:
李捷(1994—), 男，硕士，主要从事核反应堆物理分析研究

通讯作者:
李云召(1984—), 男，副教授，主要从事中子输运/扩散理论及其数值计算方法、压水堆堆芯物理计算方法研究与程序开发; yunzhao@mail.xjtu.edu.cn

中图分类号: TL327
计量
- 文章访问数: 1511
- HTML全文浏览量: 202
- PDF下载量: 247
- 被引次数: 10
出版历程
- 收稿日期: 2017-04-15
- 修回日期: 2017-09-15
- 刊出日期: 2018-01-15

Weighted Monte Carlo solution of neutron kinetics equations

Xi'an Jiaotong University, Xi'an 710049, China

摘要

摘要: 为了实现基于蒙特卡罗方法的中子动力学计算，在传统的直接蒙特卡罗动力学方法的基础上，提出了一种加权蒙特卡罗动力学方法。该方法通过引入粒子权重的概念，隐式考虑中子俘获反应和裂变反应过程中中子数目的变化，避免了模拟粒子的数目随时间的变化，降低了统计偏差，消除了程序计算过程中粒子的存库操作，提高了计算精度。基于单能点堆模型，开发了中子动力学计算程序NECP-Dandi，进行了大量数值验证与分析，包括无缓发中子、单组缓发中子、六组缓发中子、正阶跃反应性引入、负阶跃反应性引入、正脉冲反应性、负脉冲反应性和正线性反应性引入等情况。数值结果表明，相比于直接蒙特卡罗动力学方法，加权蒙特卡罗动力学方法在计算结果的精度和计算效率上有较为明显的改进，程序结构更为简洁。
- 蒙特卡罗方法 /
- 中子动力学 /
- 直接蒙特卡罗方法 /
- 加权蒙特卡罗方法 /
- 点堆
Abstract: The solution of time dependent neutronics equations still remains a challenging problem. A weighted Monte Carlo kinetics method (wMCk) is proposed based on traditional analog Monte Carlo kinetics method (aMCk). The "implicit capture" is introduced to avoid the problem of low efficient tallies in aMCk; the definition of particle weighting leads to a more compact simulation flow due to the elimination of stack operation to particle bank. Using this method, a code named NECP-Dandi was developed in mono-energetic point-kinetics model for numerical verification and analysis. 11 test cases with different reactivity insertions were employed to verify the method. Numerical results demonstrate that wMCk is superior to aMCk in terms of accuracy, efficiency and code structure.
- Monte Carlo method /
- neutron kinetics /
- analog Monte Carlo method /
- weighted Monte Carlo method /
- point-core model

HTML全文

稳态中子输运方程的蒙特卡罗求解方法，已经积累了大量的应用经验^[1-5]。但是对于瞬态中子输运方程的蒙特卡罗求解方法，国内外大学及科研机构于近年来才相继开展相关研究。2008年，沈华韵博士开发了瞬态蒙特卡罗程序(TMCC)^[6]；2013年，芬兰国立技术研究中心开发了物理-热工耦合的瞬态蒙特卡罗程序Serpent-2^[7]；同年，加拿大蒙特利尔工学院开发了瞬态蒙特卡罗模块OpenMC-TD^[8]；2014年，Russell等人基于Geant4平台开发了G4-Stock^[9]。上述工作中，有的未考虑显著影响中子动力学过程的缓发中子及其先驱核，有的未考虑瞬态过程中的反应性反馈效应，但均采用的是直接蒙特卡罗动力学方法，统计涨落大，计算程序复杂。在此基础上，本文提出了一种加权蒙特卡罗动力学方法。该方法通过引入粒子权重的概念，隐式考虑中子俘获反应和裂变反应过程中中子数目的变化。基于该方法，本文开发了中子动力学计算程序NECP-Dandi，并进行了大量的数值验证与分析。

1. 理论模型

对于中子输运过程，考虑到蒙特卡罗方法在空间几何、能量范围和中子飞行方向方面的固有优势^[10]，本文将重点放在时间维度上，基于单能点堆中子动力学方程开展研究。

1.1 中子动力学方程

单能点堆中子动力学方程的矩阵形式如下

$\frac{\mathrm{d} \boldsymbol{x}(t)}{\mathrm{d} t}+\boldsymbol{D}(t) \boldsymbol{x}(t)=\boldsymbol{P}(t) \cdot \boldsymbol{D}(t) \cdot \boldsymbol{x}(t)$

(1)

式中：x(t)，D(t)，P(t)分别为t时刻的解向量、输运衰变矩阵和概率权重矩阵，分别表示为

$\boldsymbol{x}(t)=\left(n(t) \quad c_1(t) \quad \cdots \quad c_I(t)\right)^{\mathrm{T}}$

(2)

$\boldsymbol{D}(t)=\left[\begin{array}{cccc} \Sigma_{\mathrm{t}}(t) v & 0 & \cdots & 0 \\ 0 & \lambda_1 & \cdots & 0 \\ 0 & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \lambda_I \end{array}\right]$

(3)

$\boldsymbol{P}(t)=\left[\begin{array}{cccc} \frac{\Sigma_{\mathrm{s}}(t)}{\Sigma_{\mathrm{t}}(t)}+\frac{\Sigma_{\mathrm{f}}(t)}{\Sigma_{\mathrm{t}}(t)} \nu(t)(1-\beta) & 1 & \cdots & 1 \\ \frac{\Sigma_{\mathrm{f}}(t)}{\Sigma_{\mathrm{t}}(t)} \nu(t) \beta_1 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\Sigma_{\mathrm{f}}(t)}{\Sigma_{\mathrm{t}}(t)} \nu(t) \beta_{\mathrm{I}} & 0 & \cdots & 0 \end{array}\right]$

(4)

式(2)~(4)中：n(t)为中子密度；c_i(t)(i=1, …, I，I为缓发中子先驱核组数)为第i组缓发中子先驱核密度；v为中子速度；Σ_t(t)为总截面随时间的变化；λ_i(i=1, …, I)为先驱核衰变常数；ν(t)为每次裂变平均子代数(包括瞬发中子和缓发中子先驱核)；β_i(i=1, …, I)为各组先驱核份额； $\beta=\sum\limits_{i=1}^I \beta_i$ 为先驱核总份额；Σ_s(t)为散射截面随时间的变化；Σ_f(t)为总截面随时间的变化。

为了便于采用蒙特卡罗方法进行求解，需要利用常数变易法，获得中子动力学方程的积分解

$\boldsymbol{x}(t)=\sum\limits_{m=0}^{\infty} \boldsymbol{x}_m(t)$

(5)

$\boldsymbol{x}_m(t)=\int_t^{\infty} \cdots \int_0^{t 2} \mathrm{~d} t_{m+1} \cdots \mathrm{d} t_1 \boldsymbol{D}\left(t_{m+1}\right) \mathrm{e}^{-\int_{t_m}^{t_{m+1}} \boldsymbol{D}(\tau) \mathrm{d} \tau} \boldsymbol{K}\left(t_{m-1} \rightarrow t_m\right) \cdots \boldsymbol{K}\left(t_{l-1} \rightarrow t_l\right) \cdots \boldsymbol{K}\left(t_0 \rightarrow t_1\right) \boldsymbol{x}(0)$

(6)

式中：下标l=0, 1，…，m+1, 表示第l次关键事件(包括中子的核反应和缓发中子先驱核的衰变)；x(0)为瞬态过程的初始时刻的初始值；算子 $\boldsymbol{K}\left(t_{l-1} \rightarrow t_l\right)=\boldsymbol{P}\left(t_l\right) \cdot \boldsymbol{D}\left(t_l\right) \cdot \mathrm{e}^{-\int_{l-1}^{l_l} \boldsymbol{D}(\tau) \mathrm{d} \tau}=\boldsymbol{P}\left(t_l\right) \cdot f\left(t_{l-1} \rightarrow t_l\right)$ 包含了两个物理意义明确的乘子：f(t_l－1→t_l)为粒子由t_l－1时刻存活至t_l时刻的概率密度函数，P(t_l)为粒子在经过第l次关键事件后产生的子代粒子的种类和数目。

1.2 直接蒙特卡罗动力学方法

直接蒙特卡罗动力学方法(aMCk)的主要思想是对所有粒子进行逐一模拟。具体的模拟过程如下。

(1) 对于一个在t_l－1时刻产生的中子，其存活时间Δt_l可以从f(t_l－1→t_l)抽样得出

$\Delta t_l=-\frac{\ln \xi}{\Sigma_{\mathrm{t} v}}$

(7)

式中：ξ为随机数。由此可确定中子与原子核发生第l次碰撞的时刻

$t_l=t_{l-1}+\Delta t_l$

(8)

如果该时刻超出用户规定的时间间隔，即t_l>t_final，则终止模拟；反之继续。

(2) 中子与原子核会发生三种核反应：中子俘获、中子散射和裂变。对应的概率为Σ_c(t_l)/Σ_t(t_l)，Σ_s(t_l)/Σ_t(t_l)和Σ_f(t_l)/Σ_t(t_l)，其中Σ_c(t_l), Σ_s(t_l), Σ_f(t_l), Σ_t(t_l)依次表示t_l时刻的俘获截面、散射截面、裂变截面以及总截面。通过离散抽样，得到第l次核反应的类型。

(3) 如果发生中子俘获反应，终止中子的模拟。

(4) 如果发生中子散射反应，抽样获得散射后的子代中子的运动方向和能量，模拟回到步骤(1)。

(5) 如果发生中子裂变反应，将会有ν个子代粒子产生。考虑到平均每次裂变产生的子代粒子数ν不是一个整数，模拟过程中每次裂变产生的子代粒子数目为[ν+ξ]，其中ξ为随机数。其中，保留一个粒子继续模拟，其他粒子存入堆栈中。

(6) 对于每一个子代粒子，通过离散抽样获得其种类。子代粒子为瞬发中子的概率为1－β，模拟回到步骤(1)；子代粒子为第i组缓发中子先驱核的概率为β_i，继续第(7)步。

(7) 如果模拟的对象为缓发中子先驱核，其存活时间也可以由f(t_l－1→t_l)抽样获得

$\Delta t_l=-\frac{\ln \xi}{\lambda_i}$

(9)

由此可确定缓发中子先驱核衰变产生缓发中子的时刻

$t_l=t_{l-1}+\Delta t_l$

(10)

如果该时刻超出用户规定的时间间隔，即t_l>t，则终止模拟；反之模拟过程循环至步骤(1)。

在该方法中，如果在粒子的历史中，一次中子俘获反应发生在t时刻之前，那么这个粒子的历史就对t时刻的解向量x(t)没有任何贡献；其次，裂变反应会产生多于1个的子代粒子，需要将暂不模拟的粒子进行存储，导致程序结构的复杂和占用物理内存的增加；最后，粒子的每一个行为都需要通过随机抽样确定，这带来了强的统计涨落效应，最终导致了统计结果的方差较大。

1.3 加权蒙特卡罗动力学方法

加权蒙特卡罗动力学方法(wMCk)，定义权重因子ν′为粒子对解向量的贡献。与直接蒙特卡罗动力学方法相比，加权蒙特卡罗动力学方法主要有两点不同。

首先，为了消除俘获反应造成的中子计数丢失，定义新的中子俘获截面、中子裂变截面和平均每次裂变释放的粒子数如式(11)~式(13)所示

$\Sigma_{\mathrm{c}}^{\prime}=0$

(11)

$\Sigma_{\mathrm{f}}^{\prime}=\Sigma_{\mathrm{c}}+\Sigma_{\mathrm{f}}$

(12)

$\nu^{\prime}=\nu \frac{\Sigma_f}{\Sigma_c+\Sigma_f}$

(13)

其次，在散射过程中，(n, 1n)反应前后的中子数目保持不变，权重因子在散射过程中也不会发生变化；(n, xn)反应时权重因子会改变x倍。同时，在裂变过程中，为了体现该过程子代粒子的数目变化，权重因子会被乘以ν′。通过这种方法，瞬态过程中产生的中子和缓发中子先驱核不需要进行存库和取出的操作，程序结构得到了简化，内存占用也随之减少。

2. 数值结果

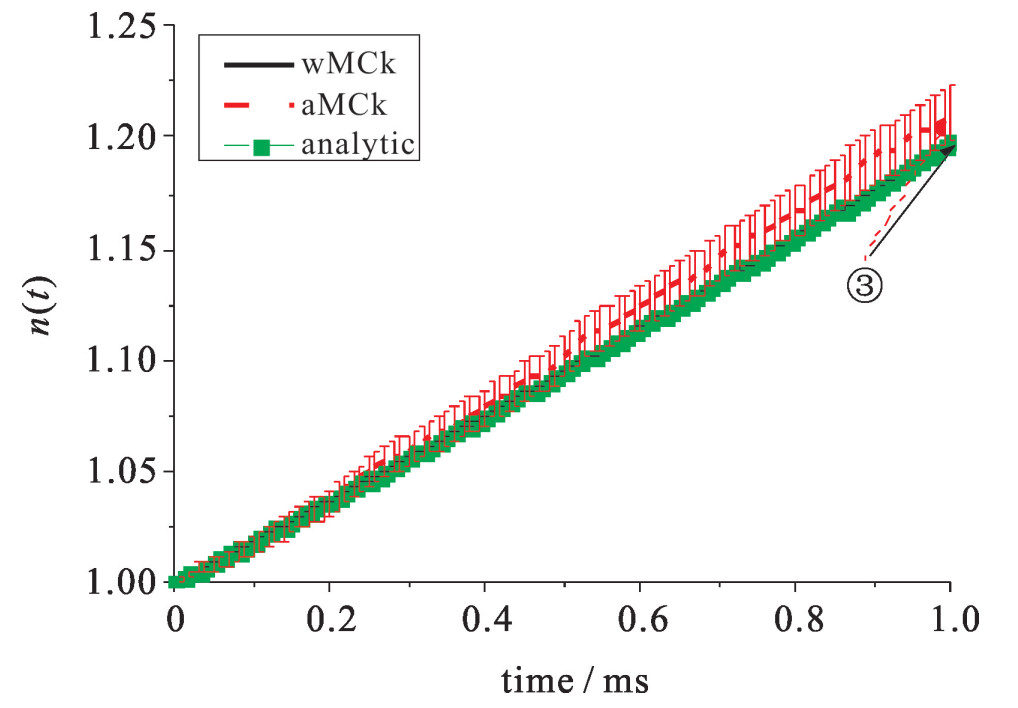
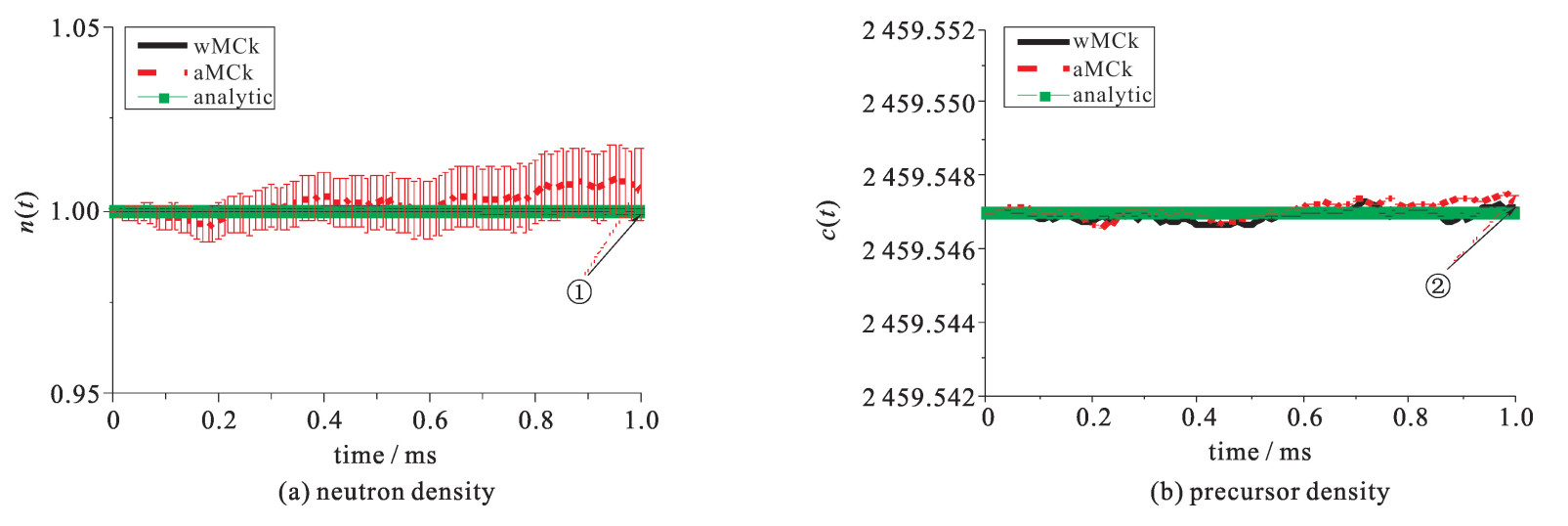
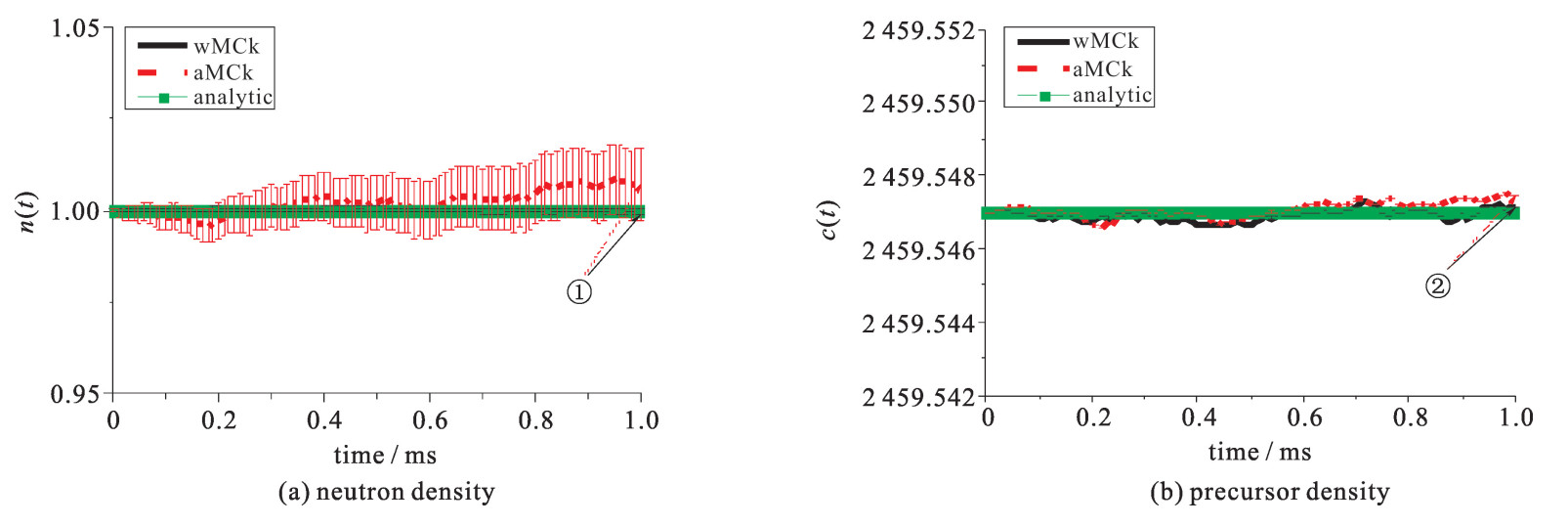
本文采用Fortran 90开发了蒙特卡罗中子动力学计算程序NECP-Dandi，并利用11个测试算例进行了数值验证与分析。参考解由解析方法(analytic)或全隐式向后差分方法(FDM)给出。所有算例的初始状态都是中子密度为1.0的临界状态。表 1列出了各算例的细节，表 2列出了使用的截面数据，模拟的瞬态持续时间均为1 ms。统计偏差由中心极限定理给出，置信度为0.95；相对偏差指蒙特卡罗方法获得的数值解相对于参考解的偏差。各算例在最后一个模拟时间点上的中子密度统计偏差(δ_errR)和相对偏差(δ_errS)详见表 3，表中首列对应图 1~5中的标注。

表 1 11个测试算例

Table 1. Definition of 11 test cases

case	No. of precursor group	reactivity insertion	duration of insertion/ms	No. of initial particle/10⁶
1	1	0	1	2500
2	6	0	1	2500
3	0	+0.006 5	1	1
4	0	-0.006 5	1	1
5	1	+0.006 5	1	2500
6	1	-0.006 5	1	2500
7	6	+0.006 5	1	2500
8	6	-0.006 5	1	2500
9	6	+0.006 5	0.1	2500
10	6	-0.006 5	0.1	2500
11	6	≈0.03t	100	2500

下载: 导出CSV

| 显示表格

表 2 单群宏观截面

Table 2. Macroscopic cross-section utilized in reactivity insertion

ρ	Σ_t/cm^-1	Σ_s/cm^-1	Σ_f/cm^-1	ν	v/(cm·s^-1)
0	0.165 258	0.156 187	0.003 657 47	2.48	3.046 655 10×10⁶
+0.006 5	0.165 258	0.156 187	0.003 681 40	2.48	3.046 655 10×10⁶
-0.006 5	0.165 258	0.156 187	0.003 633 84	2.48	3.046 655 10×10⁶
0.65t	0.165 258	0.156 187	0.003 657 47+0.000 109 724t	2.48	3.046 655 10×10⁶

下载: 导出CSV

| 显示表格

表 3 最后一个时间点的统计误差与相对误差

Table 3. Largest statistic and relative errors

No.	wMCk		aMCk
No.	δ_errR/%	δ_errS	δ_errR/%	δ_errS
①	-0.014	6.56×10^-4	0.73	9.76×10^-3
②	5.38×10^-6	2.67×10^-7	1.91×10^-5	5.51×10^-7
③	3.83×10^-3	6.75×10^-5	1.06	1.24×10^-2
④	-3.48×10^-3	6.67×10^-5	0.559	1.35×10^-2
⑤	-0.12	6.62×10^-4	0.76	9.44×10^-3
⑥	1.40×10^-6	2.93×10^-7	2.79×10^-5	5.97×10^-7
⑦	0.098 9	6.62×10^-4	1.02	1.01×10^-2
Note: Numbers in the first column correspond to those marked in Figures 1-5.

下载: 导出CSV

| 显示表格

图 1 算例1中子密度与缓发中子先驱核密度的数值结果

Figure 1. Numerical results in case 1

下载: 全尺寸图片幻灯片

图 2 算例3中子密度与缓发中子先驱核密度的数值结果

Figure 2. Numerical result in case 3

下载: 全尺寸图片幻灯片

图 3 算例4中子密度与缓发中子先驱核密度的数值结果

Figure 3. Numerical result in case 4

下载: 全尺寸图片幻灯片

图 4 算例6中子密度与缓发中子先驱核密度的数值结果

Figure 4. Numerical results in case 6

下载: 全尺寸图片幻灯片

图 5 算例10的中子密度数值结果

Figure 5. Neutron density in case 10

下载: 全尺寸图片幻灯片

算例1和2均为临界问题，不同之处只在于缓发中子先驱核组数。图 1为算例1的中子密度和缓发中子先驱核浓度随时间的变化。可以看出：对于中子密度n(t)，直接蒙特卡罗动力学方法(aMCk)的统计偏差(9.76×10^-3)大于加权蒙特卡罗动力学方法(wMCk)的统计偏差(6.56×10^-4)，且前者的结果波动更大；缓发中子先驱核浓度c(t)中，波动仍然存在，但由于绝对数值较大，两种方法的差异缩小。

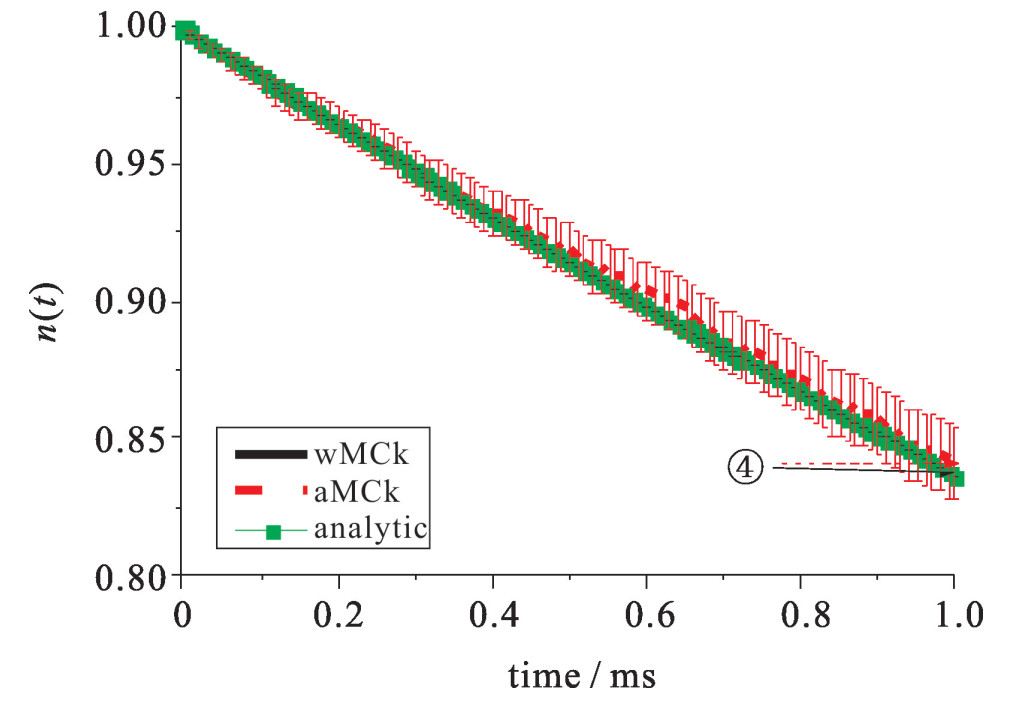
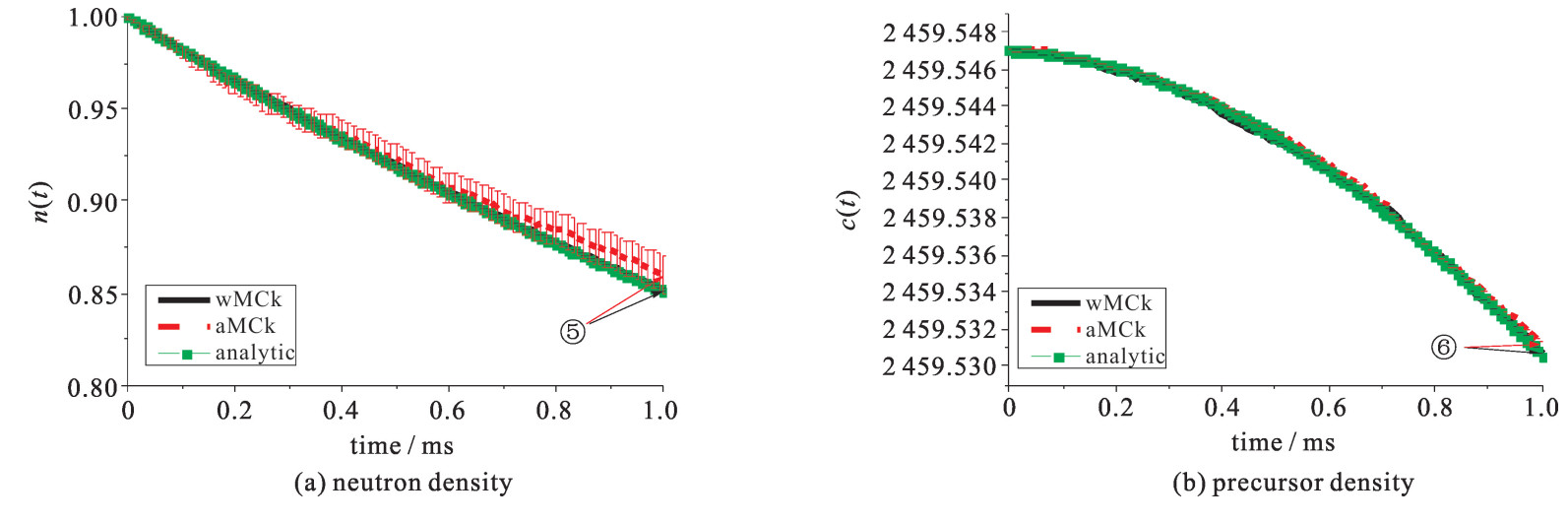
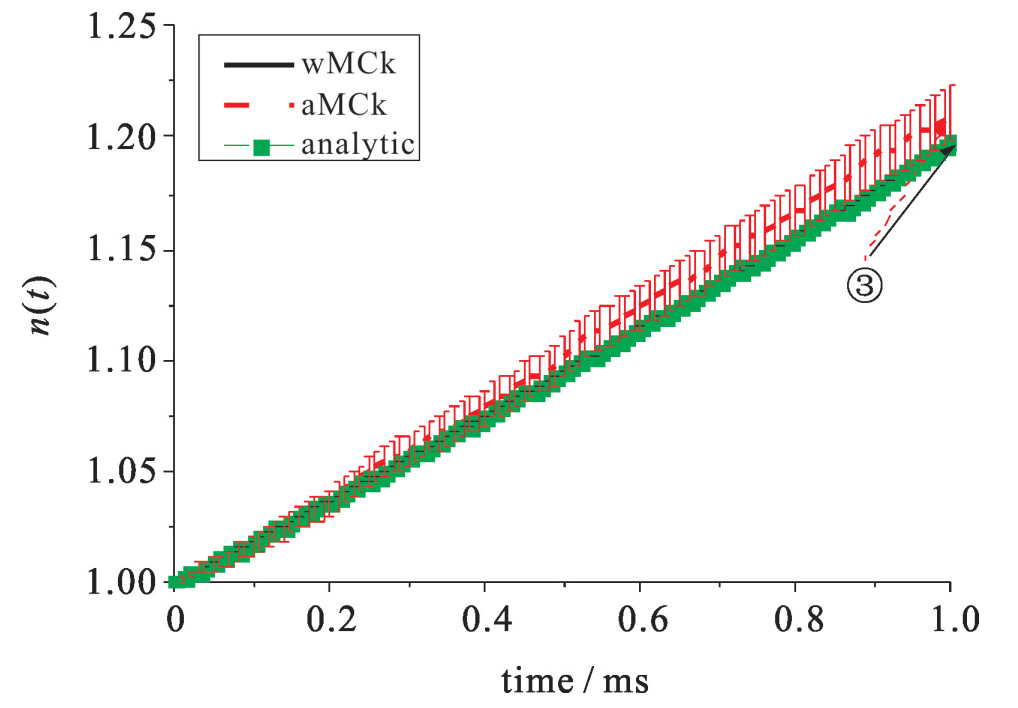
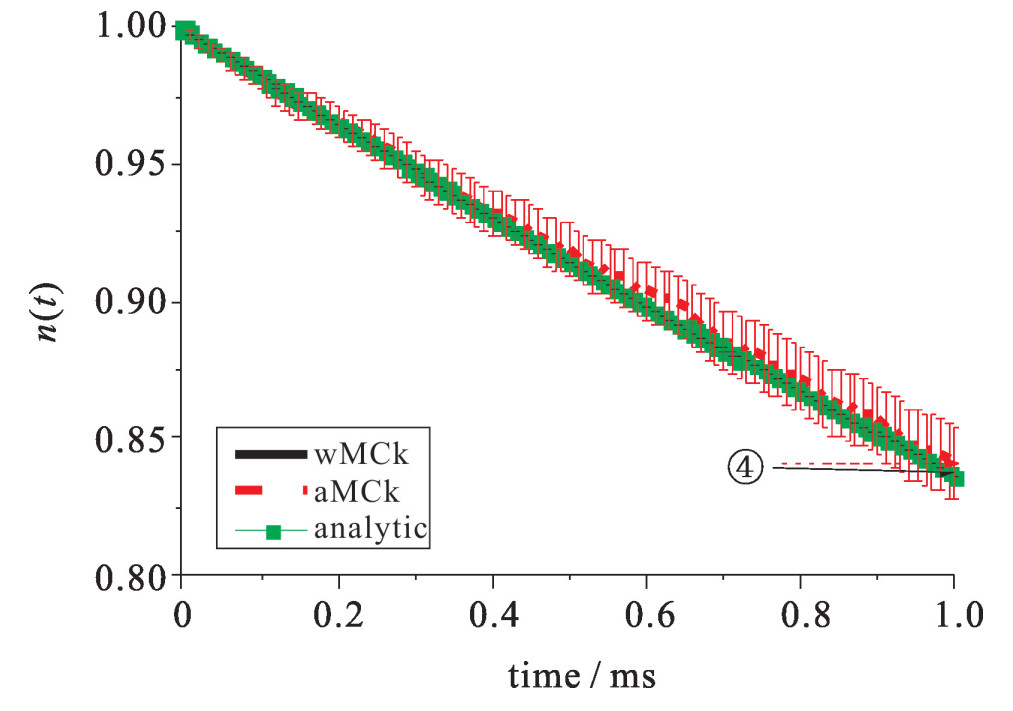
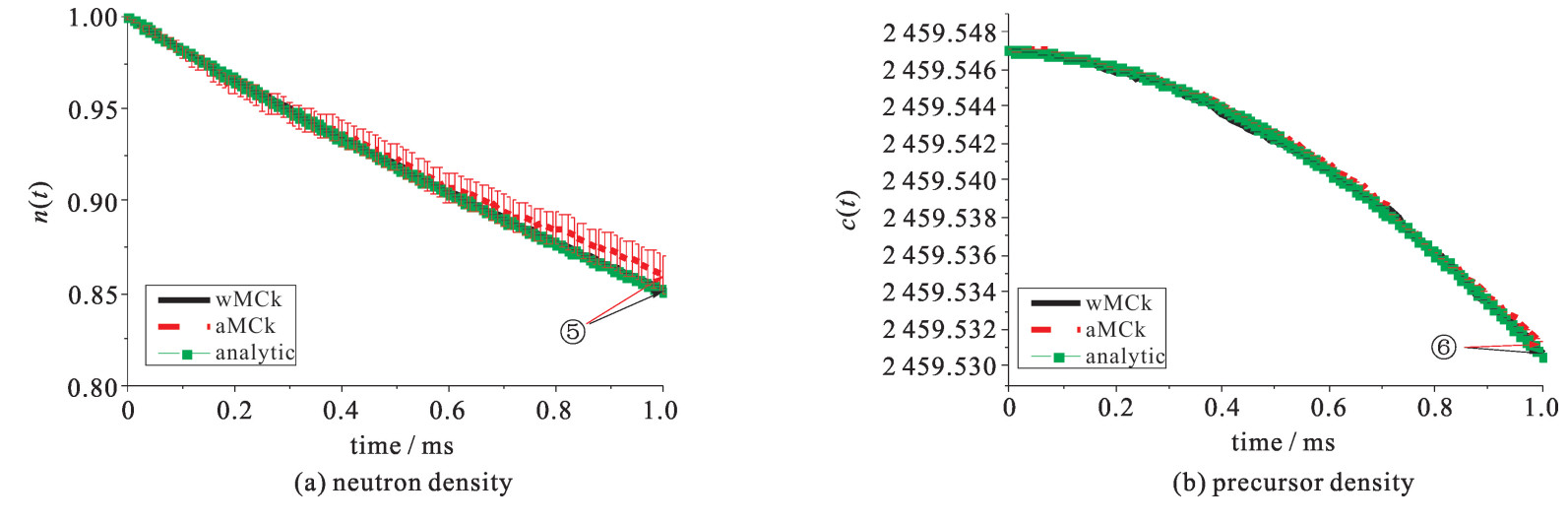
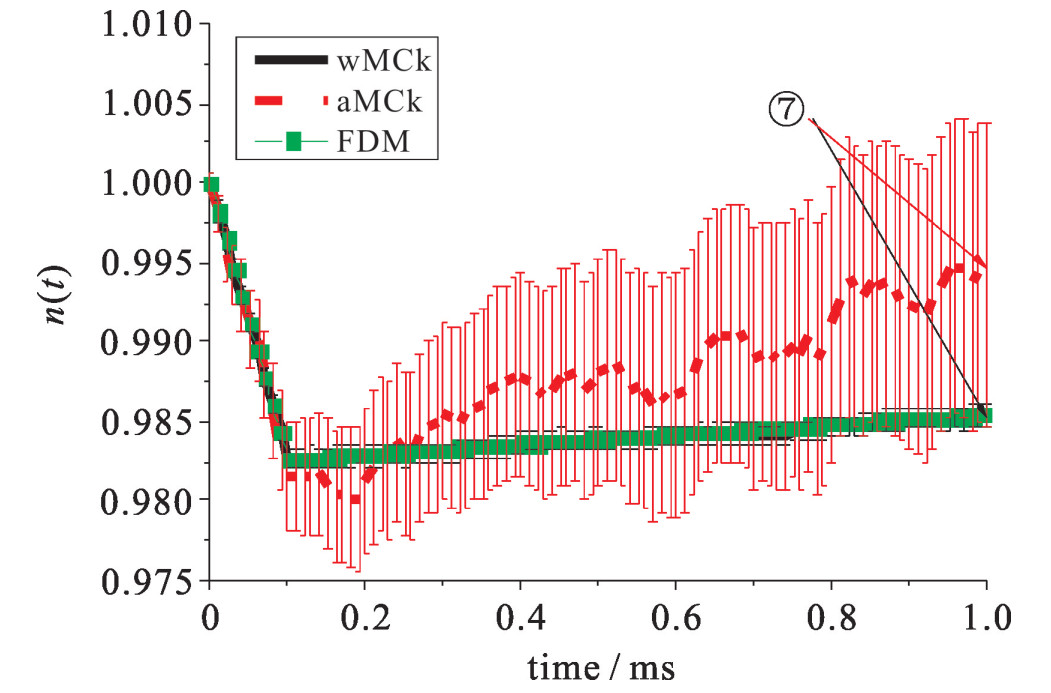
图 2和图 3为算例3和4的中子密度，图 4展示了算例6的中子密度和先驱核浓度。图 5展示了算例10的中子密度的数值结果。算例9和10分别为正脉冲和负脉冲反应性的算例，其目的是为了模拟弹棒和插棒事故。如图 5所示，在脉冲反应性终止之后，中子密度和先驱核浓度会趋于一个新的稳定状态。参考解由全隐式差分算法(FDM)给出。

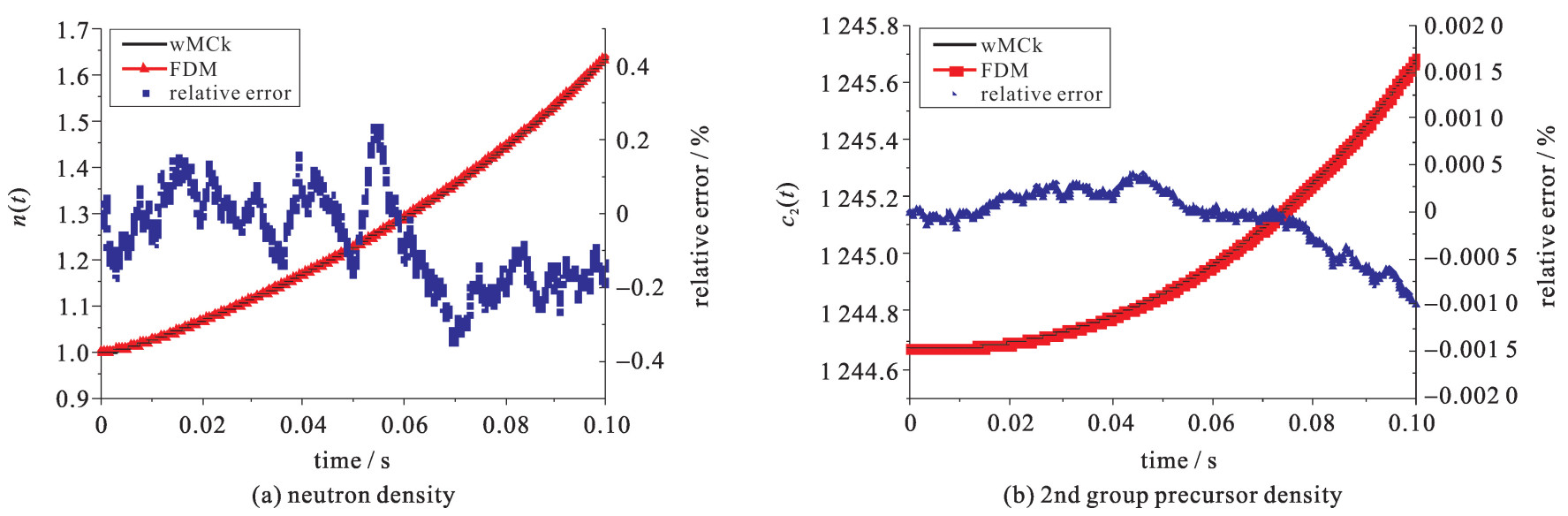
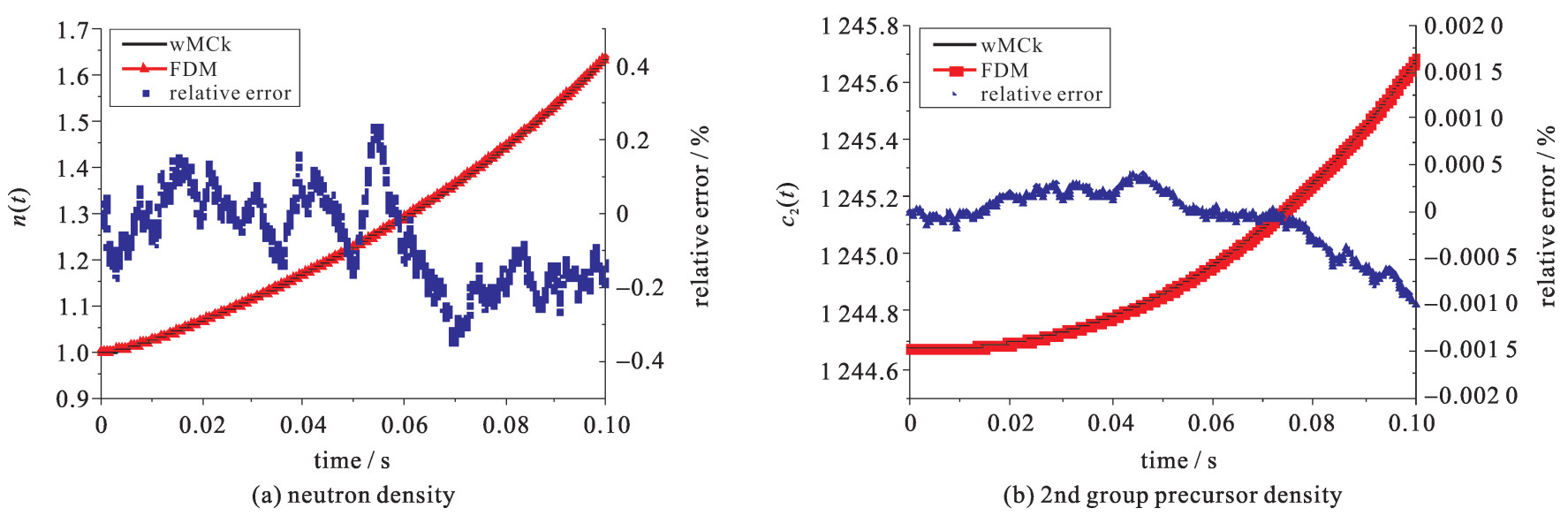
算例11为正的近似线性的反应性引入，用以分析控制棒提棒过程中的中子和先驱核浓度随时间的变化，结果如图 6所示，c₂(t)表示第二组缓发中子先驱核密度。由于使用直接蒙特卡罗动力学方法计算持续时间为100 ms的算例11时，计算所需的时间无法预估。在相同的计算时间要求内，加权蒙特卡罗动力学方法给出了较为精确的解，而直接蒙特卡罗动力学方法无法完成计算。因此，图 6中只给出了加权蒙特卡罗动力学方法的结果。

图 6 算例11中子密度与第二组缓发中子先驱核密度的数值结果

Figure 6. Part of numerical results in case 11

下载: 全尺寸图片幻灯片

3. 结论

为了利用蒙特卡罗方法求解中子动力学方程，本文提出了一种加权蒙特卡罗动力学方法，并将其与现有的直接蒙特卡罗动力学方法进行了比较。为了验证基于该方法开发的程序，设计了11个算例。数值结果显示，该方法较传统的直接蒙特卡罗动力学方法，具有更高的精度。同时，该方法利用权重概念，对裂变反应产生的子代粒子进行了简化处理，减少了子代粒子的支链历史，使程序结构更为简约。在将来的工作中，需将单能点堆动力学模型扩展为三维连续能量模型，反应性反馈效应也需考虑。

图 1 算例1中子密度与缓发中子先驱核密度的数值结果

Figure 1. Numerical results in case 1

下载: 全尺寸图片幻灯片

图 2 算例3中子密度与缓发中子先驱核密度的数值结果

Figure 2. Numerical result in case 3

下载: 全尺寸图片幻灯片

图 3 算例4中子密度与缓发中子先驱核密度的数值结果

Figure 3. Numerical result in case 4

下载: 全尺寸图片幻灯片

图 4 算例6中子密度与缓发中子先驱核密度的数值结果

Figure 4. Numerical results in case 6

下载: 全尺寸图片幻灯片

图 5 算例10的中子密度数值结果

Figure 5. Neutron density in case 10

下载: 全尺寸图片幻灯片

图 6 算例11中子密度与第二组缓发中子先驱核密度的数值结果

Figure 6. Part of numerical results in case 11

下载: 全尺寸图片幻灯片

表 1 11个测试算例

Table 1. Definition of 11 test cases

case	No. of precursor group	reactivity insertion	duration of insertion/ms	No. of initial particle/10⁶
1	1	0	1	2500
2	6	0	1	2500
3	0	+0.006 5	1	1
4	0	-0.006 5	1	1
5	1	+0.006 5	1	2500
6	1	-0.006 5	1	2500
7	6	+0.006 5	1	2500
8	6	-0.006 5	1	2500
9	6	+0.006 5	0.1	2500
10	6	-0.006 5	0.1	2500
11	6	≈0.03t	100	2500

下载: 导出CSV

表 2 单群宏观截面

Table 2. Macroscopic cross-section utilized in reactivity insertion

ρ	Σ_t/cm^-1	Σ_s/cm^-1	Σ_f/cm^-1	ν	v/(cm·s^-1)
0	0.165 258	0.156 187	0.003 657 47	2.48	3.046 655 10×10⁶
+0.006 5	0.165 258	0.156 187	0.003 681 40	2.48	3.046 655 10×10⁶
-0.006 5	0.165 258	0.156 187	0.003 633 84	2.48	3.046 655 10×10⁶
0.65t	0.165 258	0.156 187	0.003 657 47+0.000 109 724t	2.48	3.046 655 10×10⁶

下载: 导出CSV

表 3 最后一个时间点的统计误差与相对误差

Table 3. Largest statistic and relative errors

No.	wMCk		aMCk
No.	δ_errR/%	δ_errS	δ_errR/%	δ_errS
①	-0.014	6.56×10^-4	0.73	9.76×10^-3
②	5.38×10^-6	2.67×10^-7	1.91×10^-5	5.51×10^-7
③	3.83×10^-3	6.75×10^-5	1.06	1.24×10^-2
④	-3.48×10^-3	6.67×10^-5	0.559	1.35×10^-2
⑤	-0.12	6.62×10^-4	0.76	9.44×10^-3
⑥	1.40×10^-6	2.93×10^-7	2.79×10^-5	5.97×10^-7
⑦	0.098 9	6.62×10^-4	1.02	1.01×10^-2
Note: Numbers in the first column correspond to those marked in Figures 1-5.

下载: 导出CSV

参考文献(10)

[1]	Wang Kan. RMC—A Monte Carlo code for reactor core analysis[J]. Annals of Nuclear Energy, 2015, 82(1): 121-129. https://www.sciencedirect.com/science/article/pii/S0306454914004484
[2]	Leppanen J. A new assembly-level Monte Carlo Neutron transport code for reactor physics calculations[C]//International Conference on Mathematics & Computational Methods Applied to Nuclear Science & Engineering. 2005, 1871: 192-204.
[3]	李刚, 张宝印, 邓力, 等. 蒙特卡罗粒子输运程序JMCT研制[J]. 强激光与粒子束, 2013, 25(1): 158-162. doi: 10.3788/HPLPB20132501.0158 Li Gang, Zhang Baoyin, Deng Li, et al. Development of Monte Carlo particle transport code JMCT. High Power Laser and Particle Beams, 2013, 25(1): 158-162 doi: 10.3788/HPLPB20132501.0158
[4]	孙光耀, 宋婧, 郑华庆, 等. 超级蒙特卡罗计算软件SuperMC2.0中子输运计算校验[J]. 原子能科学技术, 2013, 47(s2): 520-525. https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS2013S2030.htm Sun Guangyao, Song Jing, Zheng Huaqing, et al. Benchmark of neutron transport simulation capability of super Monte Carlo calculation program SuperMC2.0. Atomic Energy Science and Technology, 2013, 47(s2): 520-525 https://www.cnki.com.cn/Article/CJFDTOTAL-YZJS2013S2030.htm
[5]	X-5 Monte Carlo Team. MCNP－A general Monte Carlo N-particle transport code, version 5[R]. 2008-02-01.
[6]	Shen Huayun. Research on direct simulation method for neutron continuous-energy spatial kinetics. Beijing: Tsinghua University, 2008: 132-251
[7]	Leppanen J. Development of a dynamic simulation mode in serpent 2 Monte Carlo code[C]//International Conference on Mathematics & Computational Methods Applied to Nuclear Science & Engineering. 2013: 117-204.
[8]	Mahjoub M, Koclas J. OpenMC-TD, a new module for Monte Carlo time dependent simulations used to simulate a CANDU6 Cell LOCA accident[C]//7^th International Conference on Modelling and Simulation in Nuclear Science and Engineering. 2015: 54-67.
[9]	Russell L, Buijs A, Jonkmans G. G4-STORK: A Geant-4 based Monte Carlo reactor kinetics simulation code[J]. Ann Nucl Energy, 2014, 71(1): 451-461. https://www.sciencedirect.com/science/article/pii/S030645491400156X
[10]	谢仲生, 邓力. 中子输运理论数值计算方法[M]. 西安: 西北工业大学出版社, 2005. Xie Zhongsheng, Deng Li. Numerical calculation method of neutron transport theory. Xi'an: Northwestern Polytechnical University Press, 2005

施引文献

期刊类型引用(8)

1.	杜子韦华，张晓琴，朱洪斌，肖鹏，余翔，谢彦召. 高频电磁干扰对传输线耦合全波建模方法. 强激光与粒子束. 2023(02): 70-76 . 本站查看
2.	秦锋，毛从光，崔志同，聂鑫，陈伟. HEMP传导环境下变压器等效电路模型的建立及验证. 现代应用物理. 2021(02): 41-46 . 百度学术
3.	张士荣，吴莲. 基于云平台的同步电机远程数据采集与监视控制系统设计. 电子测试. 2020(10): 82-83+93 . 百度学术
4.	谢彦召，刘民周，陈宇浩. 国家关键基础设施电磁恢复力. 强激光与粒子束. 2019(07): 6-13 . 本站查看
5.	张举丘，梁志珊. 高空核爆电磁脉冲E_2部分对架空管道的影响. 电子学报. 2019(08): 1762-1767 . 百度学术
6.	秦锋，钟少武，崔志同，刘清，毛从光. 核安保典型系统电磁脉冲效应试验研究. 强激光与粒子束. 2019(11): 69-75 . 本站查看
7.	束国刚，杜子韦华，黄玮，陈宇浩，陈卫华，周熠，翟守阳，何奇，谢彦召. 核电站最小安全系统电磁脉冲效应试验研究. 强激光与粒子束. 2018(10): 53-58 . 本站查看
8.	吕亚洲. 浅议数据采集及集中监控系统设计与应用. 电脑迷. 2016(03): 33 . 百度学术

其他类型引用(2)

资源附件(0)

访问统计

点击查看大图

图(6) / 表(3)

计量

文章访问数: 1511
HTML全文浏览量: 202
PDF下载量: 247
被引次数: 10

1. 理论模型
1.1 中子动力学方程
1.2 直接蒙特卡罗动力学方法
1.3 加权蒙特卡罗动力学方法
2. 数值结果
3. 结论

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

求解中子动力学方程的加权蒙特卡罗方法

doi: 10.11884/HPLPB201830.170242

作者简介:
李捷(1994—), 男，硕士，主要从事核反应堆物理分析研究

通讯作者:
李云召(1984—), 男，副教授，主要从事中子输运/扩散理论及其数值计算方法、压水堆堆芯物理计算方法研究与程序开发; yunzhao@mail.xjtu.edu.cn

计量

Weighted Monte Carlo solution of neutron kinetics equations

1. 理论模型

1.1 中子动力学方程

1.2 直接蒙特卡罗动力学方法

1.3 加权蒙特卡罗动力学方法

2. 数值结果

3. 结论

期刊类型引用(8)

其他类型引用(2)

计量

目录

1. 理论模型

1.1 中子动力学方程

1.2 直接蒙特卡罗动力学方法

1.3 加权蒙特卡罗动力学方法

2. 数值结果

3. 结论

留言板

求解中子动力学方程的加权蒙特卡罗方法

doi: 10.11884/HPLPB201830.170242

作者简介: 李捷(1994—), 男，硕士，主要从事核反应堆物理分析研究

通讯作者: 李云召(1984—), 男，副教授，主要从事中子输运/扩散理论及其数值计算方法、压水堆堆芯物理计算方法研究与程序开发; yunzhao@mail.xjtu.edu.cn

计量

出版历程

Weighted Monte Carlo solution of neutron kinetics equations

1. 理论模型

1.1 中子动力学方程

1.2 直接蒙特卡罗动力学方法

1.3 加权蒙特卡罗动力学方法

2. 数值结果

3. 结论

期刊类型引用(8)

其他类型引用(2)

计量

出版历程

目录

1. 理论模型

1.1 中子动力学方程

1.2 直接蒙特卡罗动力学方法

1.3 加权蒙特卡罗动力学方法

2. 数值结果

3. 结论

作者简介:
李捷(1994—), 男，硕士，主要从事核反应堆物理分析研究

通讯作者:
李云召(1984—), 男，副教授，主要从事中子输运/扩散理论及其数值计算方法、压水堆堆芯物理计算方法研究与程序开发; yunzhao@mail.xjtu.edu.cn