Coupled stochastic-deterministic method for accelerator-driven subcritical system transient analysis
-
摘要: 针对加速器驱动次临界系统(ADS)瞬态问题，采用预估校正改进准静态方法(PCQS)处理时空中子动力学方程中的时间自变量，采用蒙特卡罗方法处理相应的空间-角度-能量自变量，重点解决了低次临界度下模拟计算不稳定的问题，验证了TWGIL-Seed-Blanket动力学基准问题和小型模拟ADS问题，得到瞬态过程的功率变化结果，与基于其他方法的程序比较，经初步验证取得了较好结果，证明了该耦合方法可行。
-
关键词:
- 加速器驱动次临界系统 /
- 瞬态分析 /
- 蒙特卡罗方法 /
- 预估校正的改进准静态方法 /
- 耦合方法
Abstract: In accelerator-driven subcritical system (ADS), the transient characteristic is quite different from that of traditional critical system due to its strong external neutron source and its fuel composition for transmutation. This paper presents a coupled stochastic-deterministic method for analysing the transient characteristic of ADS. After comparing various reactor transient calculation methods, predictor-corrector improved quasi-static method was chosen to handle the time variable of neutron space-time kinetics equation. Considering the specific neutron spectrum, Monte Carlo method was used to handle the corresponding spatial, angle and energy variables. The main problem encountered is the Monte Carlo iteration instability for slightly subcritical system. Numerical results demonstrates the effectiveness of the new method. -
图 4 功率变化及其相对误差
Figure 4. Comparison of power curve and relative error between two codes
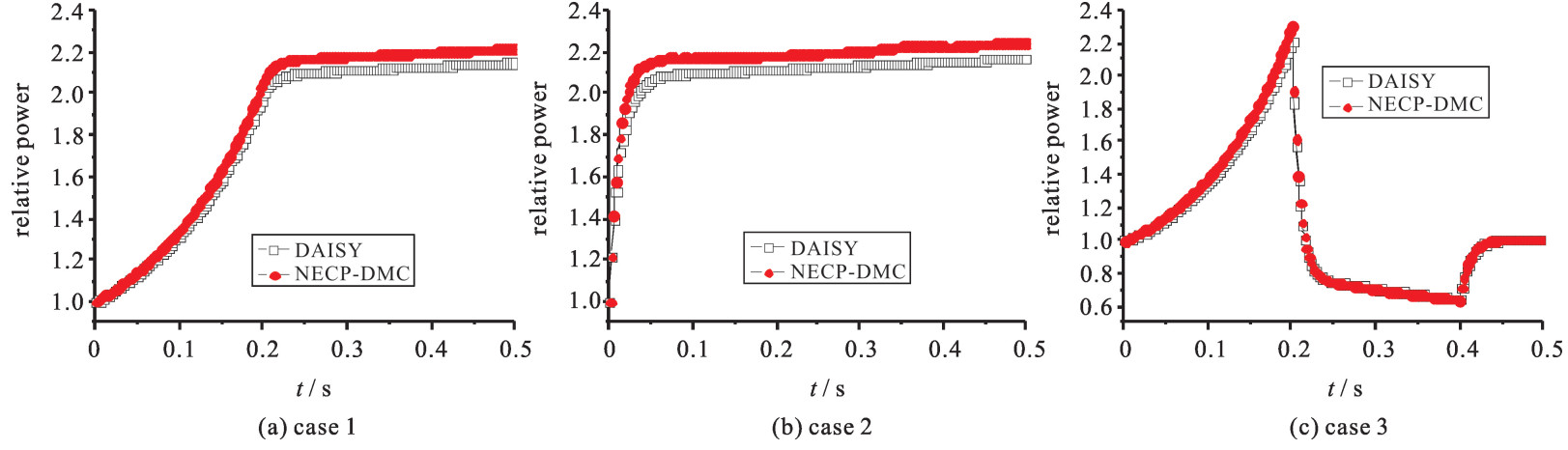
表 1 CASE 1的功率值
Table 1. Relative power of case 1
time/s reference 1 reference 2 reference 3 calculation relative error of
reference 1/%relative error of
reference 2/%relative error of
reference 3/%0.0 1.000 1.000 1.000 1.000 0.00 0.00 0.00 0.1 1.309 1.304 1.319 1.342 2.52 2.91 1.72 0.2 1.960 1.909 1.992 2.059 5.05 7.86 3.37 0.3 2.075 2.104 2.111 2.178 4.96 3.52 3.15 0.4 2.092 2.122 2.130 2.197 5.02 3.53 3.16 0.5 2.110 2.137 2.148 2.217 5.07 3.74 3.19 
下载: 导出CSV
表 2 CASE 2的功率值
Table 2. Relative power of case 2
time/s reference 1 reference 2 reference 3 calculation relative error of
reference 1/%relative error of
reference 2/%relative error of
reference 3/%0.0 1.000 1.000 1.000 1.000 0.00 0.00 0.00 0.1 2.062 2.079 2.097 2.171 5.29 4.43 3.54 0.2 2.079 2.106 2.115 2.181 4.91 3.56 3.14 0.3 2.096 2.124 2.133 2.201 5.01 3.63 3.18 0.4 2.114 2.147 2.152 2.226 5.30 3.68 3.43 0.5 2.131 2.158 2.170 2.243 5.26 3.94 3.34
下载: 导出CSV
表 3 CASE 3的功率值
Table 3. Releative power of case 3
time/s reference 1 reference 2 reference 3 calculation relative error of
reference 1/%relative error of
reference 2/%relative error of
reference 3/%0.0 1.000 1.000 1.000 1.000 0.00 0.00 0.00 0.1 1.342 1.342 1.352 1.380 2.83 2.83 2.05 0.2 2.176 2.183 2.209 2.307 6.02 5.68 4.44 0.3 0.706 0.706 0.709 0.702 -0.57 -0.57 -0.93 0.4 0.644 0.651 0.643 0.638 -0.93 -2.00 -0.84 0.5 1.007 1.007 1.002 1.008 0.10 0.10 0.60
下载: 导出CSV
表 4 材料截面信息
Table 4. Cross section of different materials
material
No.g′ Σt νΣf Σsg′→g χp g=1 g=2 g=3 g=4 1 1 0.120 561 2 0 0.103 939 0 0.016 368 1 0.000 193 3 0 0 2 0.184 457 7 0 0 0.183 602 0 0.000 755 9 0 0 3 0.322 335 3 0 0 0 0.322 175 0 0 0 4 0.297 344 8 0 0 0 0.000 037 1 0.296 585 0 0 2 1 0.133 989 1 0.011 368 5 0.100 642 7 0.029 150 5 0.000 335 9 0.000 000 1 0.599 443 7 2 0.217 553 8 0.003 330 1 0 0.213 165 2 0.001 872 2 0 0.393 927 7 3 0.347 672 8 0.002 338 7 0 0 0.342 372 3 0 0.006 628 8 4 0.837 153 0 0.169 095 9 0 0 0 0.367 162 3 0 3 1 0.134 557 2 0.011 621 3 0.100 971 9 0.029 322 4 0.000 335 4 0.000 000 1 0.599 200 3 2 0.214 679 8 0.004 265 1 0 0.210 346 1 0.001 696 9 0 0.394 153 7 3 0.348 658 4 0.003 438 3 0 0 0.343 552 7 0 0.006 646 1 4 0.877 372 6 0.175 997 5 0 0 0.000 000 1 0.368 762 4 0 4 1 0.125 998 5 0 0.097 501 1 0.028 124 9 0.000 220 0 0.000 000 2 0 2 0.186 849 8 0 0 0.185 097 0 0.001 517 9 0 0 3 0.330 537 5 0 0 0 0.330 052 0 0 0 4 0.449 236 1 0 0 0 0.000 304 5 0.439 763 0 0
下载: 导出CSV
表 5 动力学参数
Table 5. Kinetic parameters
material 1 neutron velocity/(cm·s-1) 1.921 133×109 6.934 807×108 1.900 324 ×108 8.703 439×105 energy group j=1 j=2 j=3 j=4 j=5 j=6 delayed neutron fission spectrum/χj(r, E) 1 1.090 410×10-2 1.603 450×10-2 1.403 810×10-2 4.555 420×10-2 4.320 990×10-2 6.916 650×10-2 2 8.925 330×10-1 9.408 550×10-1 9.011 270×10-1 8.929 490×10-1 8.927 940×10-1 8.492 040×10-1 3 9.656 190×10-2 4.310 910×10-2 8.483 150×10-2 6.149 560×10-2 6.399 430×10-2 8.162 780×10-2 4 0 0 0 0 0 0 delayed neutron packet fraction/βj(r) 1 8.754 830×10-7 6.471 130×10-6 4.636 330×10-6 1.140 170×10-5 4.100 530×10-6 9.442 960×10-7 2 2.820 180×10-7 2.224 650×10-6 1.582 470×10-6 3.752 390×10-6 1.327 670×10-6 3.144 220×10-7 material 2 3 1.845 090×10-7 1.695 560×10-6 1.146 240×10-6 2.555 110×10-6 9.978 850×10-7 2.694 900×10-7 4 1.304 020×10-5 1.177 470×10-4 8.025 910×10-5 1.758 460×10-4 6.428 700×10-5 1.637 520×10-5 delayed neutron precursor decay constant (1/s)/λj 1 6.847 930×10-5 2.124 550×10-4 4.243 860×10-5 3.692 210×10-5 3.864 170×10-6 2.360 010×10-7 2 2.215 370×10-5 7.350 890×10-5 1.448 260×10-5 1.204 720×10-5 1.236 420×10-6 7.679 550×10-8 3 1.440 400×10-5 5.652 230×10-5 1.036 870×10-5 8.178 590×10-6 9.869 050×10-7 7.458 460×10-8 4 1.024 590×10-3 3.929 160×10-3 7.310 170×10-4 5.605 810×10-4 6.120 390×10-5 4.250 170×10-6 neutron velocity/(cm·s-1) 2.015 869×109 6.893 608×108 1.937 460×108 9.053 391×105 delayed neutron fission spectrum/χj(r, E) 1 1.090 490×10-2 1.603 700×10-2 1.403 860×10-2 4.555 810×10-2 4.326 220×10-2 6.921 220×10-2 2 8.925 400×10-1 9.408 720×10-1 9.011 250×10-1 8.929 490×10-1 8.927 380×10-1 8.491 810×10-1 3 9.655 510×10-2 4.308 960×10-2 8.483 290×10-2 6.149 150×10-2 6.399 830×10-2 8.160 570×10-2 4 0 0 0 0 0 0 delayed neutron packet fraction/βj(r) 1 8.931 970×10-7 6.861 180×10-6 4.778 170×10-6 1.144 700×10-5 4.310 280×10-6 1.043 800×10-6 material 3 2 3.544 770×10-7 2.906 640×10-6 2.017 220×10-6 4.662 530×10-6 1.707 170×10-6 4.206 000×10-7 3 2.731 190×10-7 2.520 990×10-6 1.698 870×10-6 3.777 950×10-6 1.474 760×10-6 3.992 960×10-7 4 1.365 140×10-5 1.231 970×10-4 8.388 080×10-5 1.836 610×10-4 6.668 480×10-5 1.692 080×10-5 delayed neutron precursor decay constant (1/s)/λj 1 6.963 290×10-5 2.258 210×10-4 4.352 040×10-5 3.709 320×10-5 4.191 990×10-6 2.761 820×10-7 2 2.777 510×10-5 9.627 910×10-5 1.839 240×10-5 1.497 180×10-5 1.628 970×10-6 1.079 330×10-7 3 2.132 410×10-5 8.406 710×10-5 1.536 600×10-5 1.208 780×10-5 1.457 760×10-6 1.104 400×10-7 4 1.073 250×10-3 4.111 630×10-3 7.643 970×10-4 5.851 790×10-4 6.318 930×10-5 4.355 260×10-6 material 3 neutron velocity/(cm·s-1) 2.021 283×109 7.074 702×108 1.970 423×108 1.047 767×108 material 4 neutron velocity/(cm·s-1) 1.947 951×109 6.798 665×108 1.676 913×108 1.531 542×106
下载: 导出CSV
-
[1] NEA Nuclear Science Committee. Accelerator-driven systems (ADS) and fast reactor (FR) in advanced nuclear cycles, a comparative study[R]. OECD/NEA, 2002. [2] Oecd. Physics and safety of transmutation systems: A status report[J]. OECD Papers, 2006, 6(3): 13-13. https://www.oecd-ilibrary.org/economics/physics-and-safety-of-transmutation-systems_oecd_papers-v6-art13-en [3] Ott K O, Neuhold R J. Introductory nuclear reactor dynamics[M]. America: Amer Nuclear Society, 1985. [4] Azmy Y, Sartori E. Nuclear computational science, A century in review[M]. Germany: Springer, 2010. [5] Stacey W M. Nuclear reactor physics[M]. 2nd ed. Weinheim: WILEY-VCH Verlag GmbH & Co. KGaA, 2007. [6] Hébert A. Applied reactor physics[M]. Canada: Presses Internationals Polytechnique, 2009. [7] Dulla S, Mundb E H, Ravetto P. The quasi-static method revisited[J]. Progress in Nuclear Energy, 2008, 50: 908-920. https://www.sciencedirect.com/science/article/pii/S014919700800084X [8] 杜柄. 三维时空扩散中子动力学快速计算方法及外源驱动次临界系统中子动力学计算[D]. 西安: 西安交通大学, 2012.Du Bing. Fast calculation method for three-dimensional space-time neutron diffusion kinetics equations and study of neutron kinetics for source-driven subcritical system. Xi'an: Xi'an Jiaotong University, 2012 [9] X-5 Monte Carlo Team. MCNP—A general Monte Carlo N-particle transport code, Version 5, Volume Ⅱ: User's guide[R]. LA-UR-03-0245, 2003. [10] Raskach K F, Korobeinikov V V. Effective algorithm for calculation of a subcritical reactor with an external source[J]. Atomic Energy, 1998, 85(6): 911-915. [11] Goluoglu S. A deterministic method for transient three-dimensional neutron transport[D]. USA: University of Tennessee, Nuclear Engineering Department, 1997. [12] Ban Y, Endo T, Yamamoto A. A unified approach for numerical calculation of space-dependent kinetic equation[J]. Journal of Nuclear Science and Technology, 2012, 49(5): 496-515. [13] Zhu A, Xu Y, Graham A, et al. Transient methods for pin-resolved whole core transport using the 2D-1D methodology in MPACT[C]//M&C. 2015. [14] He M, Wu H, Zheng Y, et al. Beam transient analyses of Accelerator Driven Subcritical Reactors based on neutron transport method[J]. Nuclear Engineering & Design, 2015, 295: 489-499. https://www.sciencedirect.com/science/article/pii/S0029549315004872 [15] 何明涛. 液态金属冷却快堆的瞬态输运计算方法及次锕系核素嬗变的瞬态特性分析研究[D]. 西安: 西安交通大学, 2016.He Mingtao. Transport-based transient methods of liquid-metal cooled fast reactors and transient characteristics of minor actinides. Xi'an: Xi'an Jiaotong University, 2016 -
点击查看大图
图(4) / 表(5)
计量
- 文章访问数: 1520
- HTML全文浏览量: 354
- PDF下载量: 148
- 被引次数: 0
