A Shannon entropy-based strategy for adjusting history number of time-dependent transport problem automatically
-
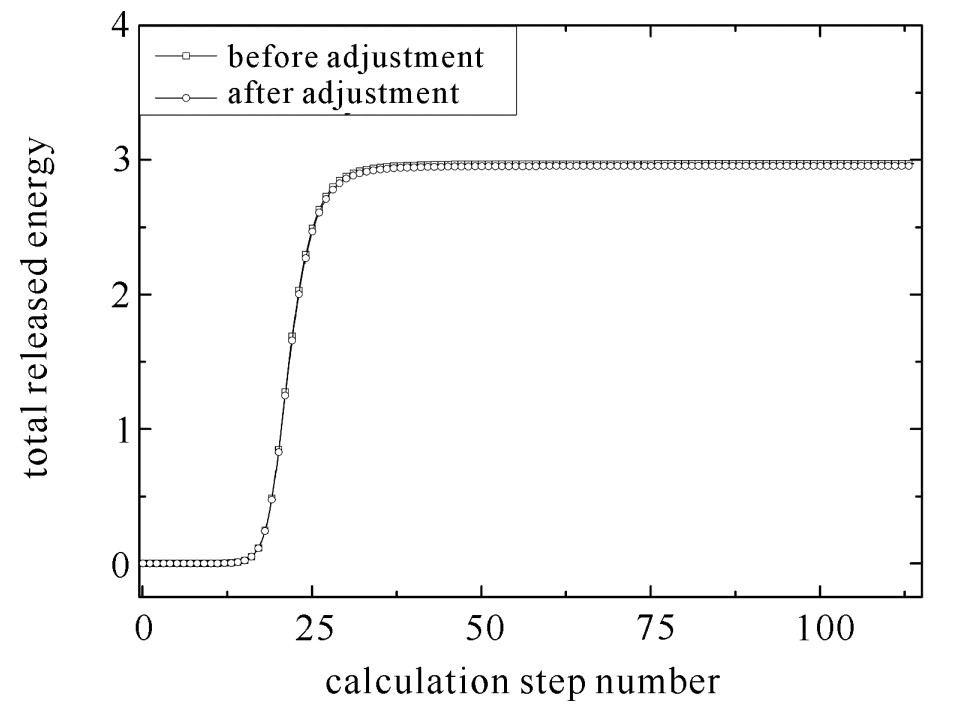
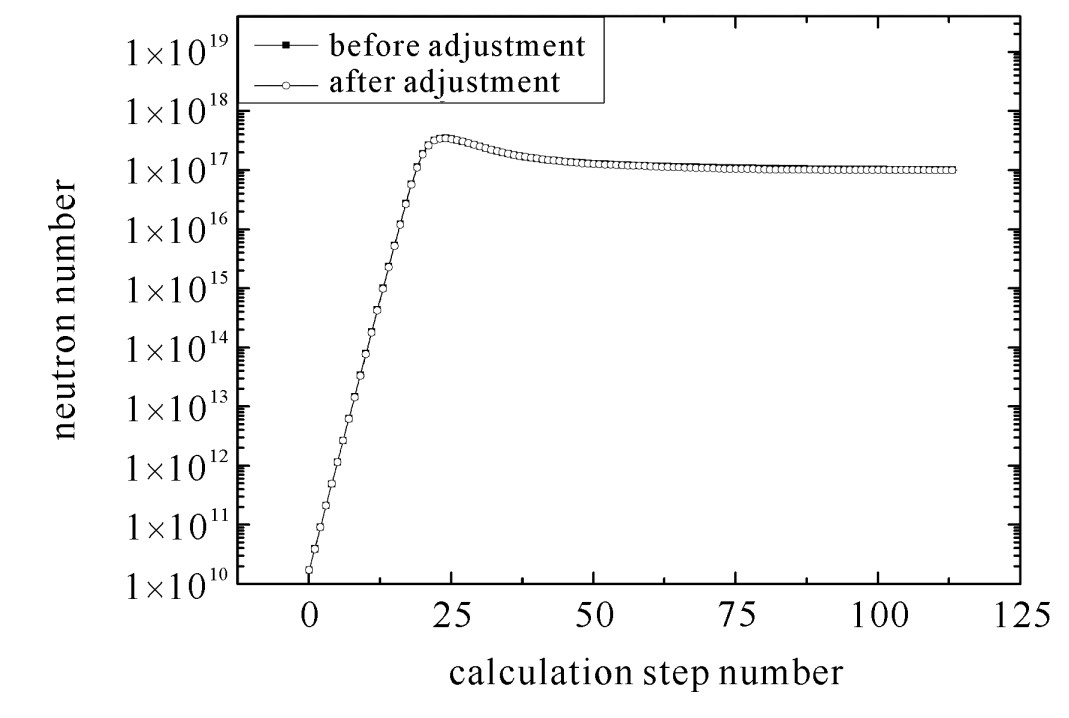
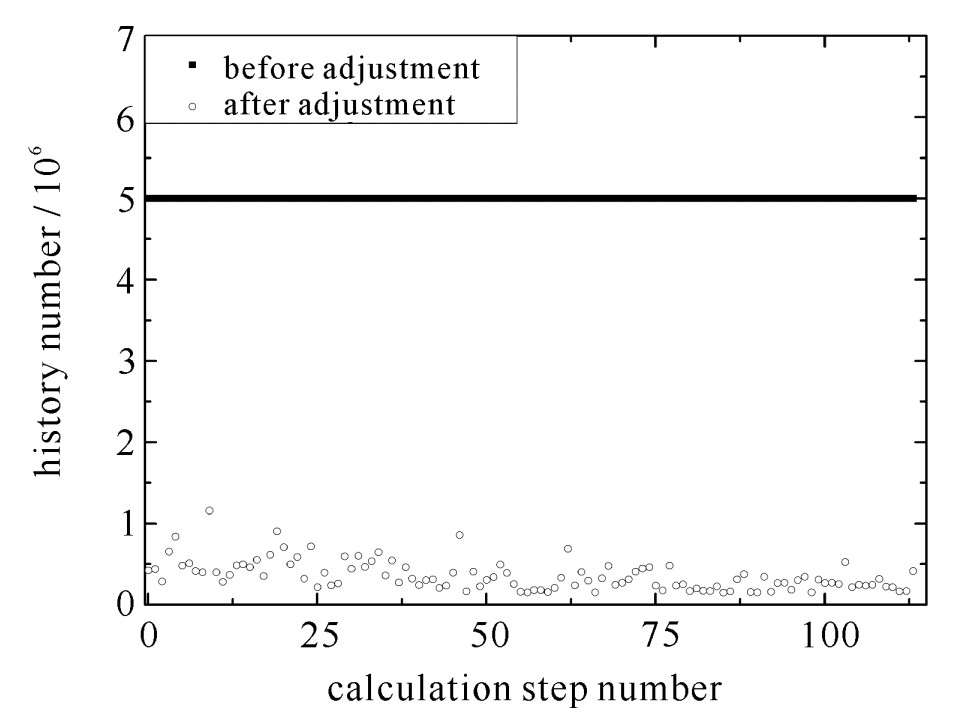
摘要: 对于非定常输运问题提出了一种基于香农熵的自动调整样本数策略。将每一计算步的总样本数划分为若干批并逐步模拟每批中的粒子, 可以在每批粒子模拟结束后通过计算得到该时间步幸存粒子属性分布对应的香农熵值。采用在线收敛性诊断方法, 一旦通过香农熵值序列判断对应的幸存粒子属性分布已经收敛, 则可以提前结束本时间步的计算。对一个空间一维非定常输运模型的计算结果表明, 该策略可以显著减少每一计算步的实际样本数且保持最终的结果基本不变, 从而减少了计算时间, 提高了计算效率。Abstract: This paper proposes a Shannon entropy-based strategy for adjusting history number of time-dependent transport problem automatically. By dividing the total history number of each step into many batches and simulating all batches one by one, we calculate the Shannon entropy of the survival particle distribution after each batch. If the on-the-fly diagnostic of convergence of entropy shows the survival particle distribution has converged, the calculation of the current step will be stopped in advance and the next step will be activated immediately. Test for a one-dimensional model shows this strategy has decreased the calculation time greatly while keeping the results almost unchanged simultaneously.
-
Key words:
- time-dependent transport /
- Shannon entropy /
- on-the-fly diagnostic
-
图 2 调整样本数前后总放能随时间的变化
Figure 2. Total released energy before and after adjusting history number
-
[1] 蓝可, 贺贤土, 赖东显, 等. 柱输运管中扩散超声速辐射的能流[J]. 物理学报, 2006, 55(7): 3789-3795. doi: 10.3321/j.issn:1000-3290.2006.07.099Lan Ke, He Xiantu, Lai Dongxian, et al. Radiative energy flux of diffusion supersonic wave in a cylinder. Acta Physica Sinica, 2006, 55(7): 3789-3795 doi: 10.3321/j.issn:1000-3290.2006.07.099 [2] Ueki T, Brown F B. Stationary modeling and informatics-based diagnostics in Monte Carlo calculation[J]. Nuclear Science and Engineering, 2005, 149(1): 38-50. doi: 10.13182/NSE04-15 [3] Naito Y, Yang J. The sandwich method for determining source convergence in Monte Carlo calculation[J]. Journal of Nuclear Science and Technology, 2004, 41(5): 559-568. doi: 10.1080/18811248.2004.9715519 [4] Ueki T, Brown F B. Stationary and source convergence diagnostics in Monte Carlo criticality calculation[C]//Proc of International Conference on Mathematics, Computational Methods & Reactor Physics. 2003. [5] Ueki T. Stationarity diagnostics with relative entropy and Wilcoxon signed rank in iterated-source Monte Carlo methods[J]. Nuclear Science and Engineering, 2008, 160(2): 242-252. doi: 10.13182/NSE160-242 [6] Ronamo P K. Application of the stochastic oscillator to assess source convergence in Monte Carlo criticality calculations[C]//Proc of International Conference on Mathematics, Computational Methods & Reactor Physics. 2009. [7] 上官丹骅, 邓力, 张宝印, 等. 非定常输运问题适应于消息传递并行编程环境的香农熵计算方法[J]. 物理学报, 2016, 65: 142801. doi: 10.7498/aps.65.142801Shangguan Danhua, Deng Li, Zhang Baoyin, et al. Efficient method of calculation Shannon entropy of non-static transport problem in message passing parallel programming environment. Acta Physica Sinica, 2016, 65: 142801 doi: 10.7498/aps.65.142801 -
下载:
点击查看大图
图(3)
计量
- 文章访问数: 1100
- HTML全文浏览量: 278
- PDF下载量: 152
- 被引次数: 0
