基于蒙特卡罗程序的核热耦合是目前反应堆高性能计算领域的重要研究方向。MIT，KIT，清华大学等机构等均已在该领域开展了研究。MIT最早实现了蒙特卡罗/热工的耦合，它是通过蒙特卡罗程序MC21及其内部的热工水力模块sink实现的^[1]。sink程序是可计算两相流的单通道程序，无法考虑堆内的横向流动，因此其温度和压力计算存在一定的偏差。KIT使用蒙特卡罗程序TRIPOLI和Serpent2分别与子通道程序SUBCHANFLOW进行耦合，同样采用的是内耦合方式^[2-3]。清华大学的RMC团队实现了RMC与COBRA-EN和COBRA-TF的耦合分别针对与组件级别和栅元级(pin-by-pin)的热工建模方式^[4-5]，其耦合方法为混合耦合，即RMC向COBRA通过外部文件传递参数，而COBRA向RMC通过内存传递参数。在反应堆多物理耦合领域，MIT于2013年提出BEAVRS基准题，其中热态满功率问题需要核热耦合的研究基础。目前MC21和RMC均初步实现了一个换料周期的计算。中物院高性能数值模拟软件中心利用自主研发的JMCT程序与子通道程序COBRA-EN进行了内耦合的研究，本文将对目前取得的阶段性成果进行展示。

1.   软件介绍

1.1   蒙特卡罗程序JMCT

JMCT是中物院高性能数值模拟软件中心自主开发的蒙特卡罗模拟软件，该软件目前可以模拟中子、光子以及电子的输运过程，考虑了包括热化在内的各种核反应，能够模拟固定源、临界本征值等各种问题。JMCT基于三维组合集合支撑框架JCOGIN，依靠JCOGIN框架高性能的数据结构和高效成熟的通信算法，具有大规模并行计算的能力，采用粒子并行和区域分解两种方式进行并行，既增加了计算效率又减小单核的内存消耗。JMCT的数据库采用ENDF/B-IIV格式，支持连续和多群能量的处理模式，并且采用在线多普勒展宽(OTF)的方式，这是能够进行核热耦合的基础。除此之外，程序加入多种减方差技巧，使收敛更加容易。目前该程序在反应堆屏蔽和堆芯计算中得到广泛引用^[6]。

1.2   子通道程序COBRA-EN

子通道程序是针对水堆堆芯结构特点设计的热工水力程序，既具有单通道程序计算速度快的特点又能考虑各个通道间的横向流动，是目前压水堆和沸水堆堆芯计算的主流热工程序。COBRA的建模方式有两种：一种为组件级，每个组件为一个子通道，组件内部进行均匀化处理；另一种为pin-by-pin，以燃料棒之间的间隙划分网格。本文采用栅元级的建模方式，燃料棒与蒙特卡罗程序一一对应，这种建模方式能使蒙特卡罗程序的计算精度最大程度得以保留。

1.3   耦合方法

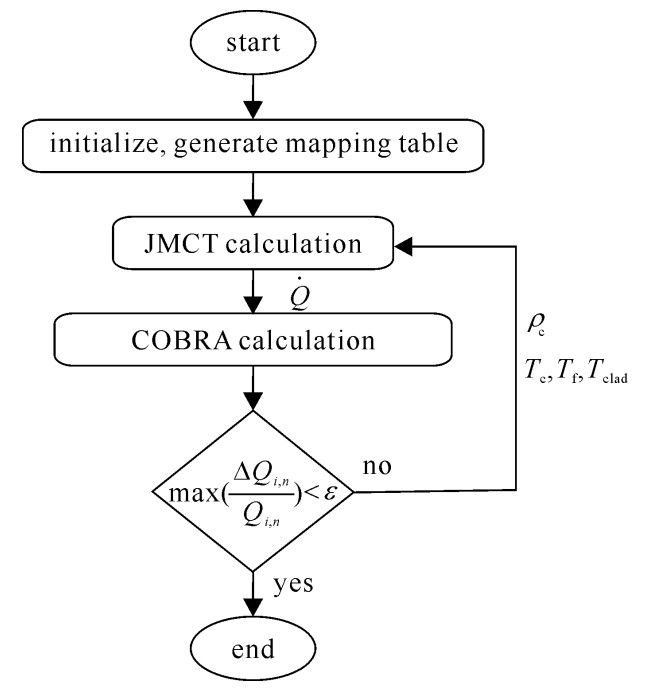
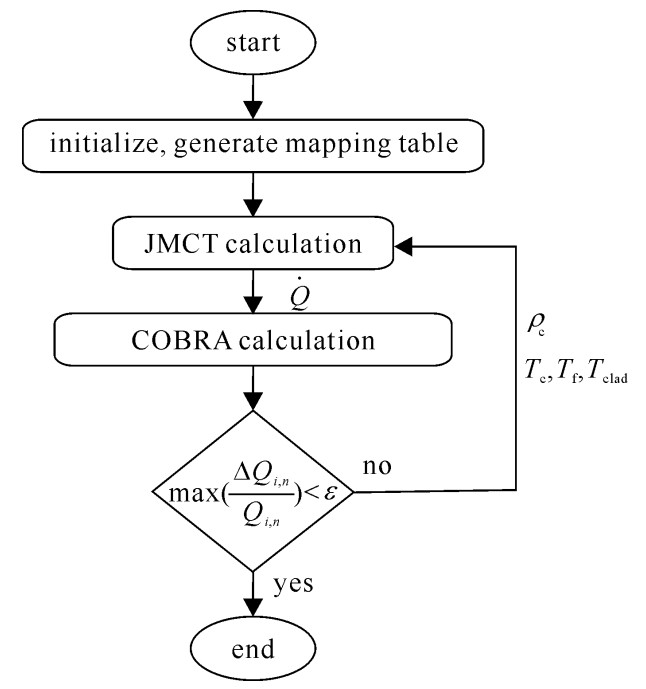
本文通过内存传递参数的方式对蒙特卡罗和热工水力程序实现内耦合，内耦合方式需要对两个程序进行整合，将COBRA程序修改后嵌入JMCT作为其内部模块。调用过程中JMCT通过功率计数提供各燃料棒的功率分布，COBRA计算返回燃料、包壳和慢化剂的温度以及慢化剂的密度，可燃毒物硼的核子密度由慢化剂的密度和初始硼浓度修正而得。耦合程序的计算流程如图 1所示，中子输运和热工计算采用Picard迭代方式进行直至收敛，收敛准则为所有燃料栅元连续两次迭代间功率计算偏差的最大值，表达形式为

图  1  耦合程序流程图

Figure  1.  Coupling scheme of JCMT and COBRA-EN

下载: 全尺寸图片 幻灯片

式中：Q为燃料栅元件n内的反应功率，i为迭代步。

2.   计算验证

2.1   计算模型

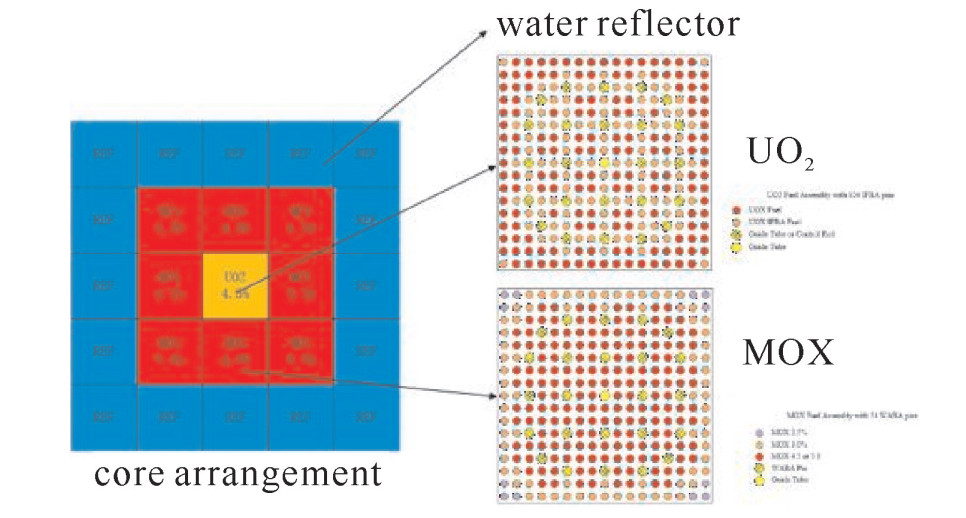
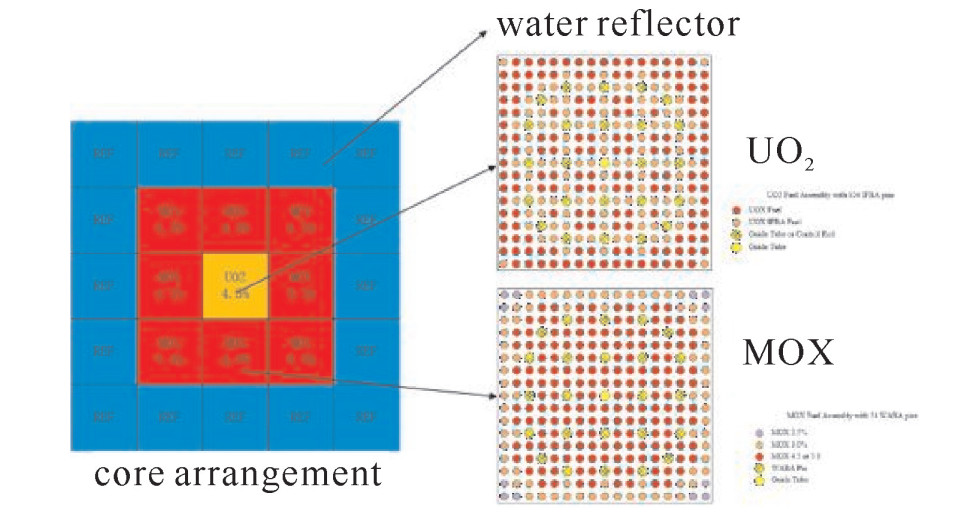
为了验证耦合方法的可行性以及计算结果的准确性，本文选取迷你堆模型的热态满功率(HFP)工况进行验算。迷你堆模型来自欧洲NURISP项目的临界硼浓度算例^[7-8]，包含3×3个燃料组件以及外侧的水反射层，堆芯包含两种组件，分别是MOX组件和UO₂组件，组件及燃料棒的详细信息来自OECD/NEA的MOX/UO₂堆芯算例库。模型的具体结构如图 2所示，物理热工参数见表 1。

图  2  迷你堆模型示意图

Figure  2.  Geometry of minicore model

下载: 全尺寸图片 幻灯片

表  1  迷你堆HFP工况的物理热工参数

Table  1.  HFP parameters of minicore

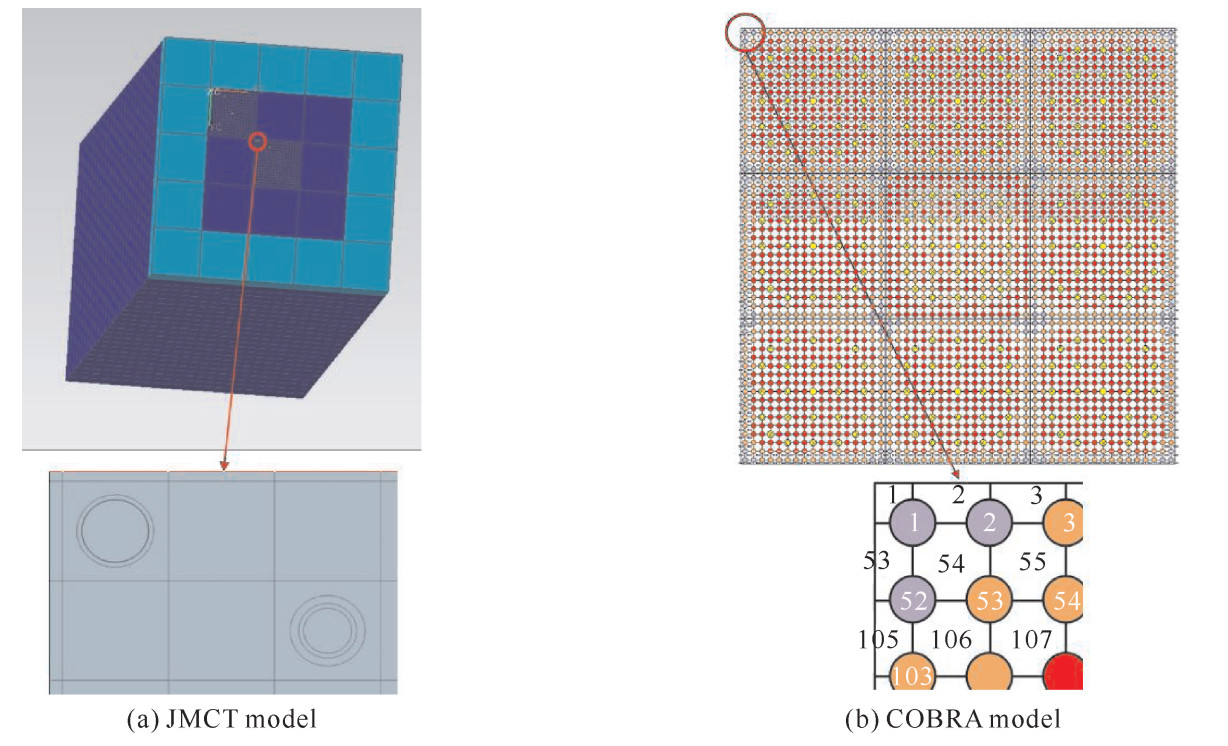
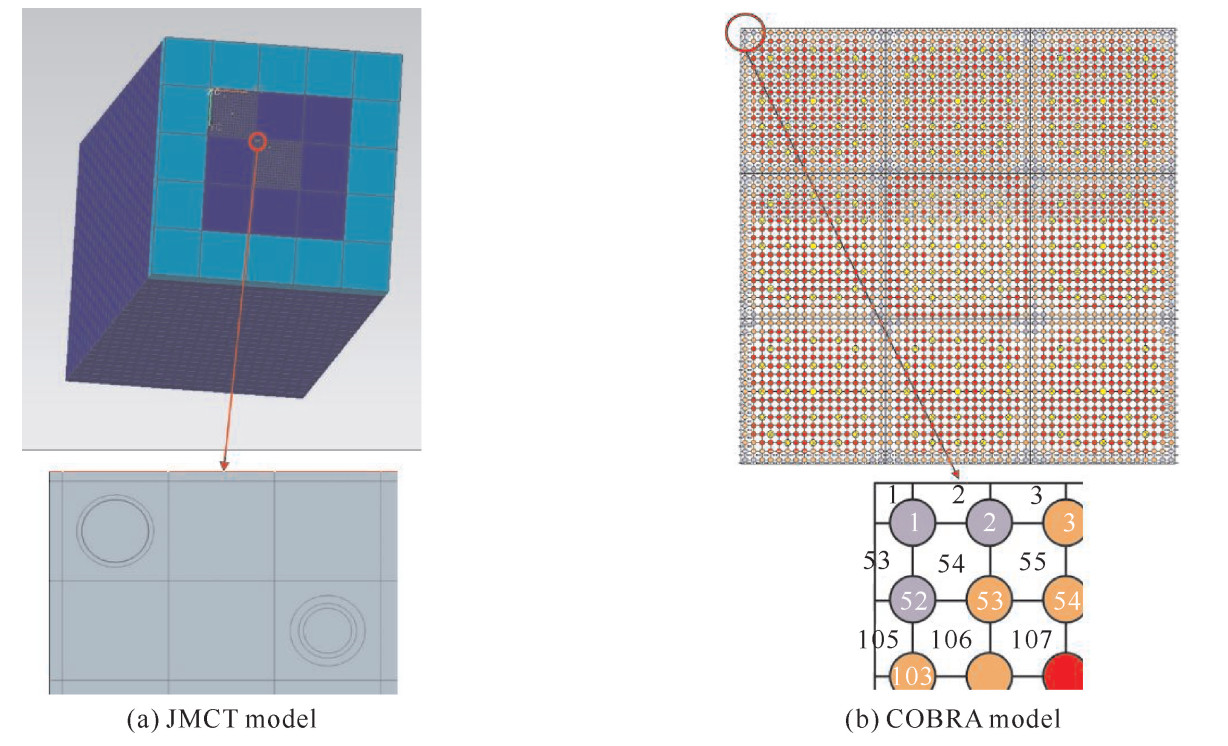
height of fuel pins /cm	assembly width /cm	assembly arrangement	power /mW	mass flow rate /(kg·s-1)	inlet temperature /K	pressure /MPa	boron concentration /ppm
365.76	21.42	17×17	100	82.12	560	15.4	200

下载: 导出CSV 

| 显示表格

使用JMCT和COBRA程序分别对上述结构进行建模。JMCT的计算模型如图 3(a)，包含算例的所有结构，模型精细至燃料棒的分层结构。为了实现与热工的pin-by-pin耦合，冷却剂区域被切割成栅元大小的网格。由COBRA程序网格规则的限制，热工模块将外部水反射层简化为绝热边界，只计算堆芯部分。同样采用pin-by-pin的建模方式，采取顺序编号规则(如图 3(b))。为了便于几何对应，JMCT和COBRA沿轴向采用相同的划分方法，均匀分为12层。

图  3  迷你堆计算模型

Figure  3.  Computation models of minicore

下载: 全尺寸图片 幻灯片

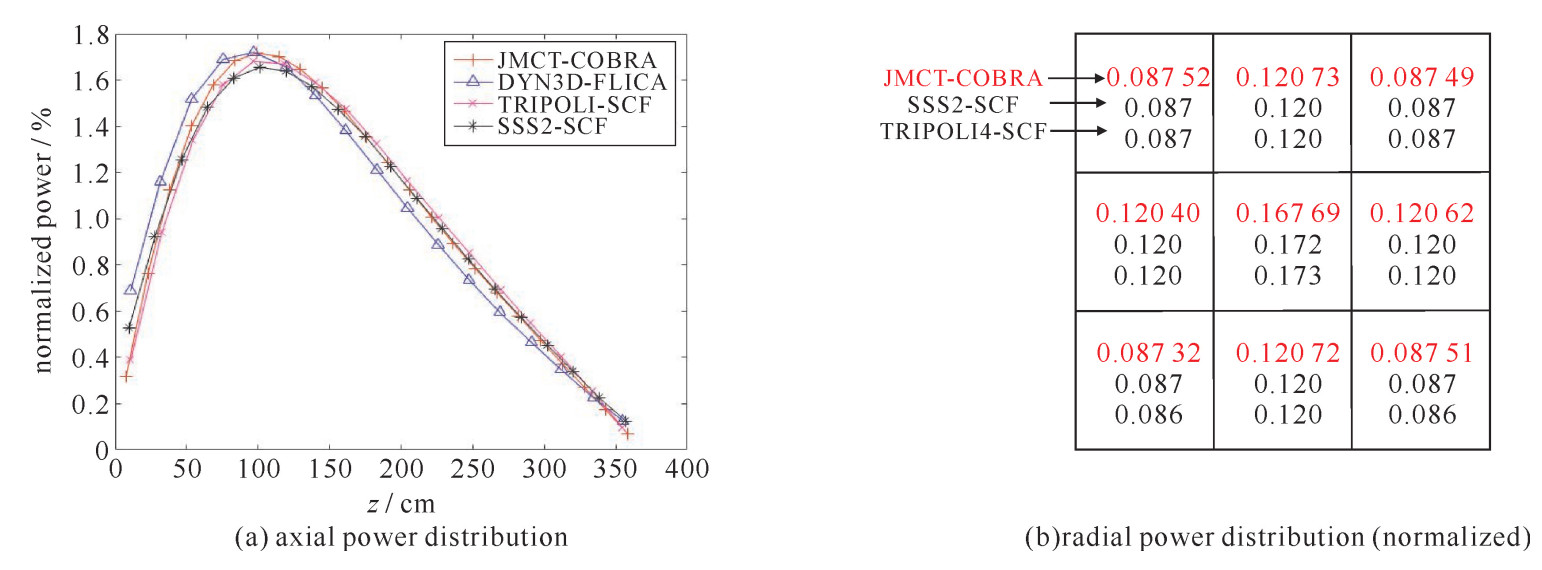
KIT和Delft大学分别利用Serpent2/SUBCHANFLOW^[3]，Tripoli/SUBCHANFLOW^[3]以及确定论程序DYN3D/FLICA^[2]对该算例进行了验算，使用的截面库均为JEFF3.1.1。本文将采用上述文献的数据对计算结果进行校验。

2.2   计算结果

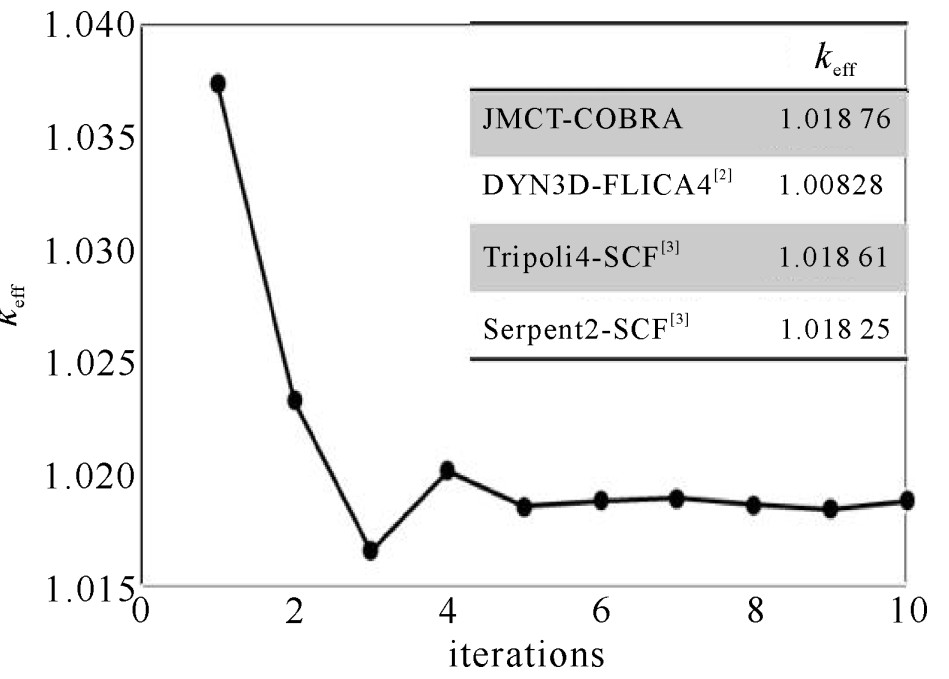
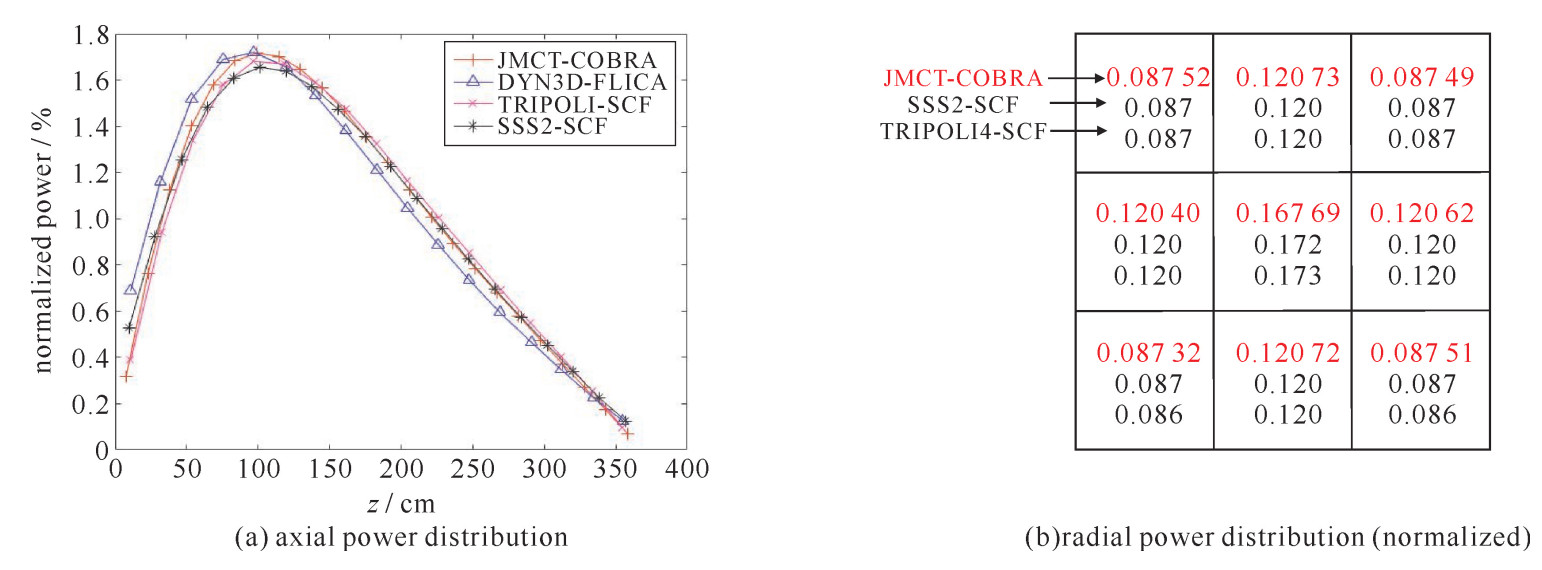
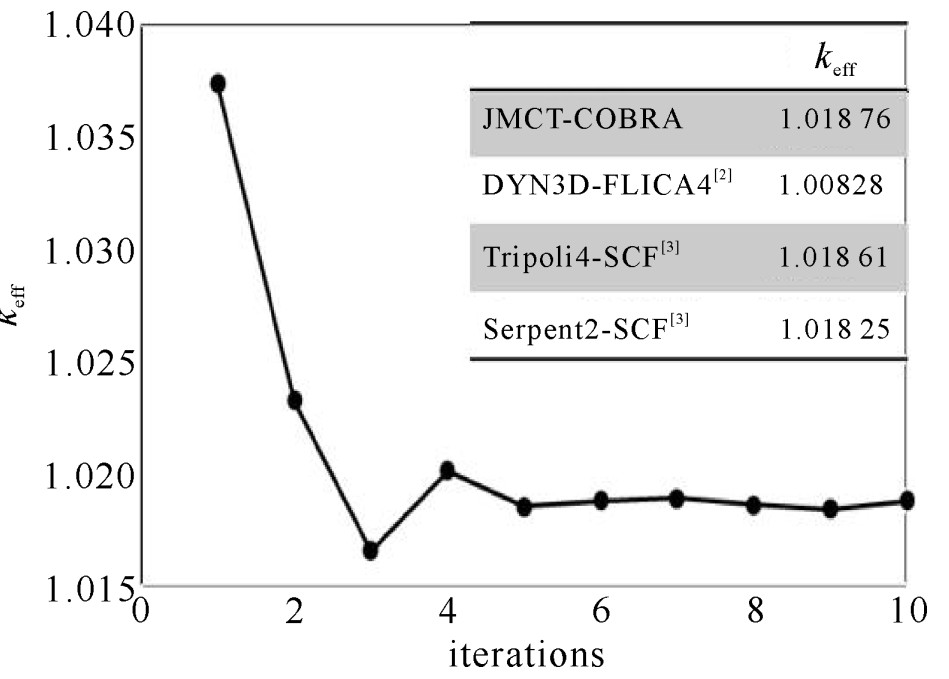
在每个耦合迭代步内，蒙特卡罗程序投入粒子数为10万/代，共计算1000代，舍弃前500代。耦合过程的最大迭代次数为10，图 4显示有效增殖系数k_eff随迭代进行的收敛情况，在第五迭代步之后k_eff便取得了较好的收敛效果。计算所得k_eff为1.018 76，与TRIPOLI和Serpent2的计算结果十分相近。迷你堆的功率分布如图 5所示，不同于热态零功率的对称功率分布，由于堆芯上层冷却剂温度偏高，根据温度的负反馈效应，真实堆芯的功率最高点下移，这与反应堆的实际情况相符，也同参考文献结果的趋势保持一致。对各个组件的总功率进行统计，与TRIPOLI/SCF以及Serpent2/SCF的差别约为3%。引起上述差异的结果可能有两个：首先计算选取的蒙特卡罗程序和子通道程序均不相同，子通道参数的设置对结果会产生显著的影响；第二TRIPOLI/SCF和Serpent2/SCF的热工水力计算均采用组件级的建模方式，忽略了组件内的温度差异，会对模型的温度和密度分布造成一定的影响。

图  4  有效增殖系数k_eff随迭代次数的收敛情况

Figure  4.  k_eff in the iteration steps

下载: 全尺寸图片 幻灯片

图  5  迷你堆的功率分布

Figure  5.  Power distributions in minicore

下载: 全尺寸图片 幻灯片

蒙特卡罗方法是一种统计学方法，计算结果存在一定的随机性。这种随机性将随着样本的增大逐渐减小，加大投入粒子数和增加代数均可达到增加样本的作用。根据1.3节的介绍，本算例采用恒定10步耦合迭代，计算结束后统计达到收敛标准(最后两次迭代间功率偏差小于1%)的燃料几何体占所有燃料的比例。表 2做出了单个迭代步内不同粒子数和代数下，达到收敛标准的几何体的比例。结果显示，增大粒子数和计算代数均能提高计算的收敛性，并且在低粒子数和计算代数区间下提升效果明显。但随着粒子数超过8×10⁵，计算代数超过1500代每迭代步，收敛性提升效果明显变差，会造成计算资源的浪费。

表  2  收敛比例与粒子数和统计代数的关系

Table  2.  Convergence ratio of power in different tracking neutrons and batches

neutrons per batch	number of batches	convergence ratio/%
1×105	1000	30.94
2×105	1000	42.26
4×105	1000	54.44
6×105	1000	61.63
8×105	1000	70.51
10×105	1000	73.50
6×105	1500	73.23
6×105	2000	83.39
6×105	3000	88.25

下载: 导出CSV 

| 显示表格

3.   结论

本文将COBRA进行修改后作为一个模块嵌入到JMCT中，实现了蒙特卡罗和热工的内耦合，解决了堆内热工反馈的问题。并通过NURISP项目的迷你堆模型对程序进行了验证，迷你堆的计算结果与TRIPOLI/SCF以及Serpent/SCF结果一致。利用小模型的计算经验，下一步将开展对BEAVRS挑战零燃耗工况的模拟。BEAVRS模型规模约为迷你堆模型的20倍，因此该工作将面临内存消耗、计算效率、计算稳定性等多种问题。作者将利用JMCT大规模并行的强大优势以及所在团队丰富的并行经验开展后续研究。