考虑中子泄漏修正的快堆蒙特卡罗少群截面参数制作与验证方法

蔡利

doi:10.11884/HPLPB201830.170254

考虑中子泄漏修正的快堆蒙特卡罗少群截面参数制作与验证方法

doi: 10.11884/HPLPB201830.170254

蔡利

中广核研究院有限公司反应堆工程设计与安全分析中心, 广东深圳 518031

详细信息

作者简介:
蔡利(1986—)，女，博士，工程师，主要从事核反应堆物理软件研发工作；caili2015@cgnpc.com.cn

中图分类号: TL329.3
计量
- 文章访问数: 1122
- HTML全文浏览量: 235
- PDF下载量: 164
- 被引次数: 0
出版历程
- 收稿日期: 2017-06-21
- 修回日期: 2017-10-17
- 刊出日期: 2018-02-15

Leakage-corrected fast reactor assembly calculation with Monte-Carlo code and its validation methodology

Cai Li

China Nuclear Power Technology Research Institute Co Ltd, Shenzhen 518031, China

摘要

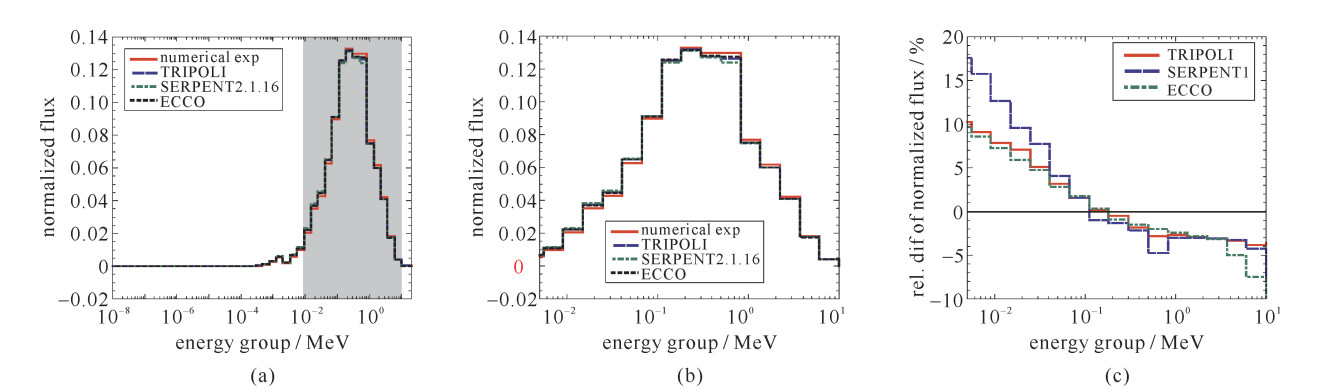
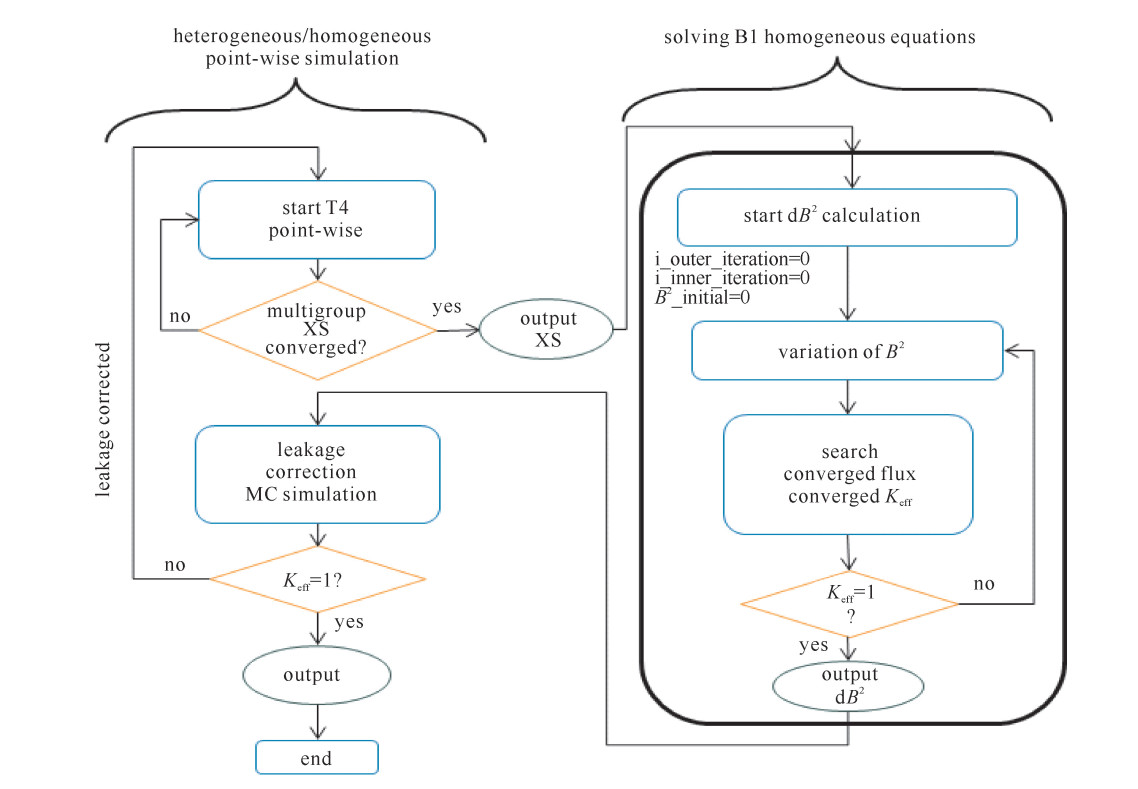
摘要: 一种基于B1均匀化方程的泄漏修正模型在连续能量蒙特卡罗程序TRIPOLI4中得以实现并且用于制作少群截面参数。此蒙卡泄漏修正模型通过在连续能量的蒙卡模拟以及求解B1均匀化方程之间迭代，最终得到蒙卡模拟下的临界状态。通过此方法得到的少群截面参数较其他蒙卡以及确定论方法有两点显著优势：用于求解B1均匀化方程的少群常数是用通过临界状态的通量谱得到的；考虑了泄漏效应的蒙卡模拟可以更真实地反映组件计算时的能谱状态。为验证此泄漏修正模型，一个由连续能量的TRIPOLI4模拟而得到的数值临界实验被用于分析与比较。通过与其他蒙卡程序SERPENT以及确定论程序ECCO进行结果对比，可证明此B1泄漏修正方法能够给出更精确的用于堆芯计算的少群截面参数。
- 泄漏模型 /
- 临界曲率 /
- 截面
Abstract: A leakage model based on B1 homogeneous equations has been implemented in continuous-energy Monte Carlo code TRIPOLI4. This leakage model algorithm iterates between the point-wise Monte Carlo simulation and a B1 homogeneous equation solver till reaching a final critical state in Monte Carlo simulation. The two advantages of our leakage model compared with the others are: we use critical flux spectrum to generate the multi-group constants for solving the B1 homogeneous equation; the leakage coefficients calculated are considered in point-wise Monte Carlo simulation. This leakage model is validated by a pre-designed numerical experiment simulated with continuous-energy TRIPOLI4 and the results obtained by this leakage model are proved to be more accurate by comparison with those from SERPENT leakage model and deterministic leakage model in ECCO code.
- leakage model /
- critical buckling /
- cross section

HTML全文

图 1 TRIPOLI4程序中泄漏修正模型的流程图

Figure 1. Leakage model algorithm in TRIPOLI4 code

下载: 全尺寸图片幻灯片

图 2 归一化临界通量密度谱比较

Figure 2. Comparison of normalized critical flux spectra

下载: 全尺寸图片幻灯片

图 3 泄漏率比较

Figure 3. Leakage rate comparison

下载: 全尺寸图片幻灯片

表 1 临界曲率比较结果

Table 1. Comparison of critical buckling values

	B²/(10^-3cm^-2)	relative diff/%
numerical curve	2.854	-
TRIPOLI4	2.823	-1.09
SERPENT	2.807	-1.65
ECCO	2.747	-3.75

下载: 导出CSV

参考文献(7)

[1]	Park H J, Shim H J, Joo H G. Generation of few group diffusion theory constants by Monte Carlo code McCARD[J]. Nuclear Science and Engineering, 2012, 172(1): 66-77.
[2]	Leppänen J. SERPENT: a continuous-energy Monte Carlo reactor physics burnup calculation code[R]. Finland: VTT Technical Research Centre of Finland. 2013.
[3]	Cho N Z, Yun S H, Lee J. Generation of homogenized nodal parameters by Monte Carlo method with non-zero leakage spectra in global-local iteration framework[J]. Transactions of the American Nuclear Society, 2009, 101: 707-710.
[4]	Yamamoto T. Monte Carlo algorithm for buckling search and neutron leakage-corrected calculations[J]. Annals of Nuclear Energy, 2012, 47: 14-20. doi: 10.1016/j.anucene.2012.04.017
[5]	Cai Li, Pénéliau Y, Diop C M, et al. P1 adaptation of TRIPOLI-4 code for the use of 3D realistic core multigroup cross section generation[C]//Joint International Conference on Supercomputing in Nuclear Application and Monte Carlo. 2013.
[6]	Rimpault G. Algorithmic features of the ECCO cell code for treating heterogeneous fast reactor assemblies[C]//International Conference on Mathematics and Computations, Reactor Physics, and Environmental Analyses. 1995.
[7]	Grimstone M J, Tullett J D, Rimpault G. Accurate treatments of fast reactor fuel assembly heterogeneity with the ECCO cell code[C]//International Conference on the Physics of Reactors: Operation, Design and Computation-PHYSOR. 1990.