二维各向异性磁等离子体的无条件稳定ADE-CNAD-FDTD算法

李建雄; 庄永佳; 李现国

doi:10.11884/HPLPB201830.170269

二维各向异性磁等离子体的无条件稳定ADE-CNAD-FDTD算法

doi: 10.11884/HPLPB201830.170269

李建雄^{1, 2,},
庄永佳^{1, 2},
李现国^{1, 2, ,}

1.
天津工业大学电子与信息工程学院，天津 300387
2.
天津市光电检测技术和系统重点实验室，天津 300387

基金项目:

国家自然科学基金项目 61372011

详细信息

作者简介:
李建雄(1969—)，男，博士，教授，主要从事计算电磁学的研究；lijianxiong@tjpu.edu.cn

通讯作者:
李现国(1981—)，男，博士，副教授，主要从事算法研究；lixianguo@tjpu.edu.cn

中图分类号: O.441.4
计量
- 文章访问数: 1190
- HTML全文浏览量: 246
- PDF下载量: 261
- 被引次数: 1
出版历程
- 收稿日期: 2017-06-29
- 修回日期: 2017-09-22
- 刊出日期: 2018-01-15

Unconditionally stable auxiliary differential equation Crank-Nicolson-approximate-decoupling FDTD algorithm for 2-D anisotropic magnetized plasma

Li Jianxiong^{1, 2
,},
Zhuang Yongjia^{1, 2},
Li Xianguo^{1, 2
, ,}

1.
School of Electronics and Information Engineering, Tianjin Polytechnic University, Tianjin 300387, China
2.
Tianjin Key Laboratory of Optoelectronic Detection Technology and Systems, Tianjin 300387, China

摘要

摘要: 针对二维各向异性磁等离子体提出一种有效的无条件稳定算法，新算法结合了辅助微分方程(ADE)方法与Crank-Nicolson approximate-decoupling(CNAD)时域有限差分算法仿真各向异性磁等离子体介质。传统的ADE-FDTD方法应用在一维各向异性色散介质具有较高的精度和效率，将提出的新算法ADE-CNAD-FDTD应用到二维各向异性磁等离子体介质中不仅解决了电磁波在具有各向异性和频率色散特性介质中传播的仿真难题，而且去除了CFL稳定性条件。该算法在保留了原有的精度情况下大幅度地提高了计算效率并成为无条件稳定的形式。给出一个算例证明该算法的有效性，通过模拟电磁波在磁等离子体中的传播，仿真结果与传统的ADE-FDTD算法对比，证实了该算法的高效率、无条件稳定性和高精度。
- 辅助微分方程 /
- Crank-Nicolson approximate-decoupling算法 /
- 时域有限差分 /
- 磁等离子体
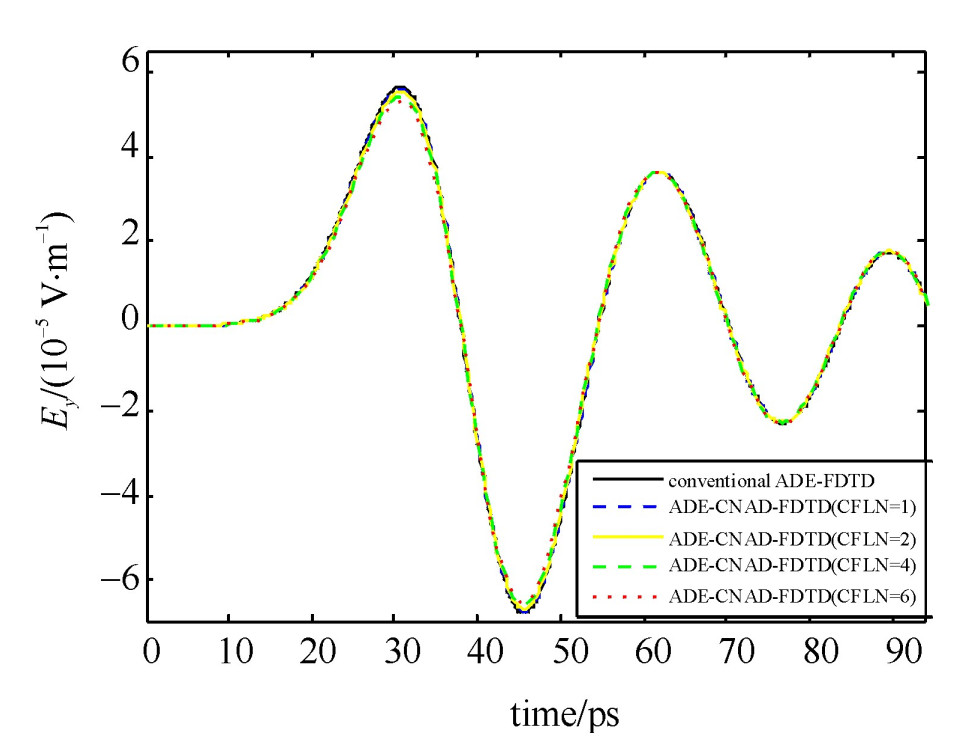
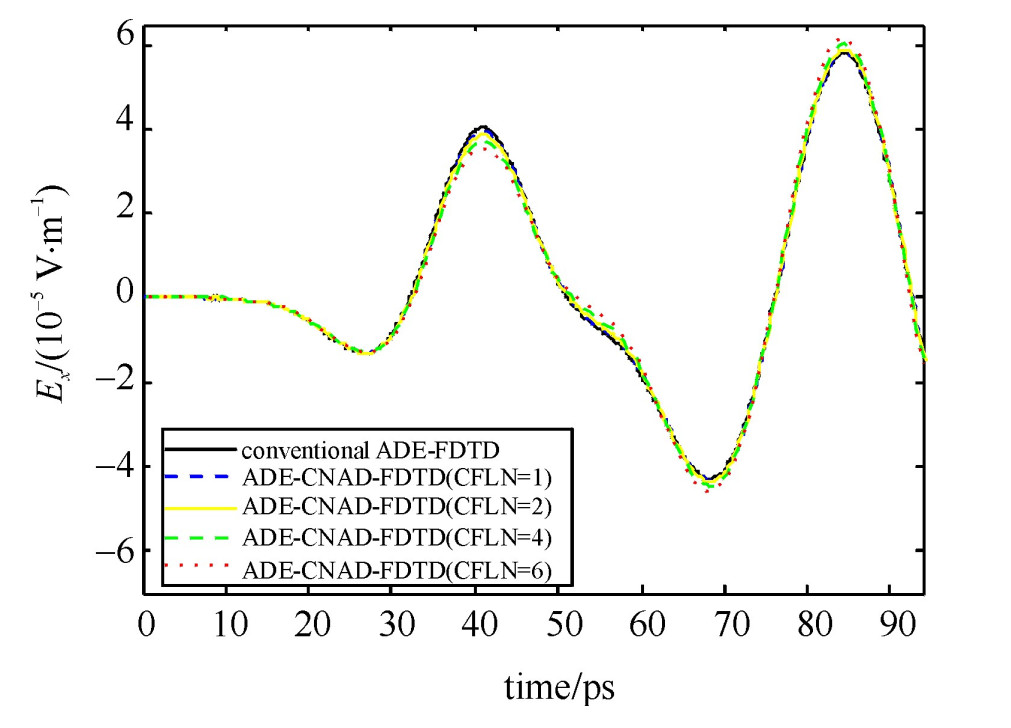
Abstract: An effective unconditionally stable implementation of the auxiliary differential equation Crank-Nicolson-approximate-decoupling finite-difference time-domain (ADE-CNAD-FDTD) algorithm for 2-D anisotropic magnetized plasma is proposed. The conventional ADE-FDTD method for 1-D anisotropic dispersive media has high efficiency and accuracy. This paper extends this method to 2-D anisotropic magnetized plasma with the CNAD scheme. The proposed formulations not only solves the problem that incorporates both anisotropy and frequency dispersion at the same time, but also eliminates the Courant-Friedrich-Levy (CFL) stability constraint. A numerical example has been carried out to validate the proposed formulations in the 2-D FDTD domain composed of anisotropic magnetized plasma. The results prove that the proposed formulations significantly save time and perform stably with acceptable accuracy.
- auxiliary differential equation (ADE) /
- Crank-Nicolson-approximate-decoupling (CNAD) /
- finite-difference time-domain (FDTD) /
- magnetized plasma

HTML全文

图 1 比较ADE-CNAD-FDTD在不同CFLN值情况下与传统ADE-FDTD的电场强度E_x

Figure 1. Comparison of electric field intensity E_x between ADE-CNAD-FDTD with different CFLNs and conventional ADE-FDTD

下载: 全尺寸图片幻灯片

图 2 比较ADE-CNAD-FDTD在不同CFLN值情况下与传统ADE-FDTD的电场强度E_y

Figure 2. Comparison of electric field intensity E_y between ADE-CNAD-FDTD with different CFLNs and conventional ADE-FDTD

下载: 全尺寸图片幻灯片

表 1 传统ADE-FDTD和ADE-CNAD-FDTD两种算法占用的时间和内存

Table 1. Time and memory used by conventional ADE-FDTD method and ADE-CNAD-FDTD method

	ADE-FDTD	ADE-CNAD-FDTD
	ADE-FDTD	CFLN=1	CFLN=2	CFLN=4	CFLN=6
time/s	78.880	167.650	80.870	40.850	27.340
memory/MB	82.604	90.844	90.872	90.760	90.876

下载: 导出CSV

参考文献(11)

[1]	Luebbers R J, Hunsberger F, Kunz K S. A frequency dependent time domain formulation for transient propagation in plasma[J]. IEEE Trans Antennas and Propagation, 1991, 39(1): 29-34. doi: 10.1109/8.64431
[2]	刘少斌, 莫锦军, 袁乃昌. 各向异性磁等离子体的辅助方程FDTD方法[J]. 物理学报, 2004, 53(7): 2233-2236. doi: 10.3321/j.issn:1000-3290.2004.07.040 Liu Shaobin, Mo Jinjun, Yuan Naichang. An auxiliary differential equation FDTD method for anisotropic magnetized plasma. Acta Physica Sinica, 2004, 53(7): 2233-2236 doi: 10.3321/j.issn:1000-3290.2004.07.040
[3]	Xu L J, Yuan N C. JEC-FDTD for 2-D conducting cylinder coated by anisotropic magnetized plasma[J]. IEEE Microwave and Wireless Components Letters, 2005, 15(12): 892-894. doi: 10.1109/LMWC.2005.859970
[4]	Liu S, Zhong S, Liu S B. Piecewise linear recursive convolution FDTD method for magnetized plasmas[J]. Journal of Systems Engineering and Electronics, 2006, 17(2): 290-295. doi: 10.1016/S1004-4132(06)60050-9
[5]	杨宏伟, 袁洪, 陈如山, 等. 各向异性磁化等离子体的SO-FDTD方法[J]. 物理学报, 2007, 56(3): 1443-1446. doi: 10.3321/j.issn:1000-3290.2007.03.034 Yang Hongwei, Yuan Hong, Chen Rushan, et al. SO-FDTD analysis of anisotropic magnetized plasma. Acta Physica Sinica, 2007, 56(3): 1443-1446 doi: 10.3321/j.issn:1000-3290.2007.03.034
[6]	Taflove A, Hagness S C. Computational electrodynamics: The finite-difference time-domain method[M]. 3rd ed. Boston: Artech House, 2005.
[7]	Namiki T. A new FDTD algorithm based on alternating-direction implicit method[J]. IEEE Trans Microwave Theory and Techniques, 1999, 47(10): 2003-2007. doi: 10.1109/22.795075
[8]	Sun G, Trueman C W. Unconditionally stable Crank-Nicolson scheme for solving two-dimensional Maxwell's equations[J]. Electronics Letters, 2003, 39(7): 595-597. doi: 10.1049/el:20030416
[9]	Lee J, Fornberg B. A split step approach for the 3-D Maxwell's equations[J]. Journal of Computational and Applied Mathematics, 2003, 158(2): 485-505. doi: 10.1016/S0377-0427(03)00484-9
[10]	Shibayama J, Muraki M. Efficient implicit FDTD algorithm based on locally one-dimensional scheme[J]. Electronics Letters, 2005, 41(19): 1046-1047. doi: 10.1049/el:20052381
[11]	Sun G, Trueman C W. Approximate Crank-Nicolson schemes for the 2-D finite-difference time-domain method for TEz waves[J]. IEEE Trans Antennas and Propagation, 2004, 52(11): 2963-2972. doi: 10.1109/TAP.2004.835142