补偿脉冲发电机放电波形优化方法

陶雪峰; 刘昆

doi:10.11884/HPLPB201830.170325

补偿脉冲发电机放电波形优化方法

doi: 10.11884/HPLPB201830.170325

陶雪峰^1,,
刘昆²

1.
航天工程大学研究生院, 北京 101400
2.
国防科技大学空天科学学院, 长沙 410073

基金项目: 国家高技术发展计划项目

详细信息

作者简介:
陶雪峰(1992－)，男，硕士，从事惯性储能脉冲功率技术研究；taoxuefeng11@sina.cn

中图分类号: TM301
计量
- 文章访问数: 1223
- HTML全文浏览量: 288
- PDF下载量: 108
- 被引次数: 5
出版历程
- 收稿日期: 2017-12-25
- 修回日期: 2018-02-20
- 刊出日期: 2018-09-15

Pulse shaping method for compulsator

Tao Xuefeng^1
,,
Liu Kun²

1.
Department of Graduate Management, Space Engineering University, Beijing 101400, China
2.
College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China

摘要

摘要: 基于一台两相四极空心补偿脉冲发电机，研究了多相脉冲电机放电波形调节的最优化问题。对补偿脉冲发电机的三种典型负载：电磁轨道炮、脉冲激光器和电热化学炮的基本特性进行了阐述，针对这三种负载分别提出了相应的优化指标，分析了量化脉冲波形对负载的适用程度，并将波形优化问题转化为函数优化问题。在建立了脉冲电机放电数学模型的基础上，使用差分进化算法对优化问题进行求解，找到最优点火角组合。对电磁轨道炮，优化指标为弹丸加速度比。将加速度比的概念进行拓展，可得到适用于脉冲激光器的尖顶脉冲。对电热化学炮，提出了“形状方差”的概念，消除了电流幅值的影响，能够较好地衡量脉冲形状的适用性。仿真结果表明，提出的脉冲波形优化指标是有效的，在智能优化算法的帮助下，能够通过控制量的组合得到不同类型负载的最优波形。
- 补偿脉冲发电机 /
- 脉冲波形调节 /
- 优化算法 /
- 负载特性 /
- 点火角
Abstract: Based on a two-phase four-poles air-core compulsator, the discharge pulse shape optimization problem is studied. The characteristics of three typical kinds of loads for compulsator: electromagnetic rail guns, flashlamps and electro-thermal chemical guns are analyzed, whose requirements for pulse shape are significantly different. Optimization indexes are proposed for different loads to quantify the fitness of discharge pulse, transferring the pulse shaping problem into function optimization problem. For electromagnetic rail guns, the optimization index is the "acceleration ratio" of the projectile, which is the ratio of maximum acceleration and average acceleration during launch process. The larger acceleration ratio is, the flatter the waveform is. By expanding the concept of acceleration ratio, this index can be applied on flashlamps. For electro-thermal chemical guns, the concept of "shape variance" is proposed to measure the pulse shape. Simulation results show that the proposed optimization indexes are effective. With the help of intelligent optimization algorithm, we can get the optimized discharge pulse for different loads. Simultaneously, it is verified that the two-phase compulsator has strong flexibility in waveform adjustment.
- compulsator /
- pulse shaping technique /
- optimization algorithm /
- load characteristic /
- firing angle

HTML全文

随着现代科技的发展，越来越多的先进技术被应用到国防领域中。近年来，各国在新概念武器方面加大了投入，发展迅速。新概念武器主要包括电磁炮、高功率微波武器、高能激光武器、电热化学炮等。虽然这些高能武器的工作机理不同，但它们都需要高功率脉冲电源(PPS)的激励或驱动。脉冲电源的种类很多，它们的储能方式及放电机理不同，都有各自的特点^[1]。就目前的发展水平来看，实际使用的脉冲电源系统(主要为脉冲电容器)体积大、质量大，往往超过武器系统本身，因此发展小型化、轻型化的高功率脉冲电源是新概念武器走向实战的重要保证^[2]。补偿脉冲发电机(CPA)是一种特殊的同步电机，通过补偿屏蔽筒、补偿线圈等结构实现磁通压缩，能够极大地降低放电时电机的瞬态电感，从而实现大电流、高功率输出^[3]。CPA采用飞轮惯性储能方式，通过机械能与电能之间的转换，能够达到极高的储能密度，且能量转换效率高，是非常有发展前景的脉冲电源方案^[4]。补偿脉冲电机类型多种多样，也可驱动不同类型的武器系统。由于不同负载的阻抗特性不同，对放电波形的需求差异也很大，CPA的脉冲波形灵活调节的能力十分重要^[5]。电机结构确定后，单相电枢的放电波形一般是固定的。通常将补偿脉冲电机设计成多相结构，通过各相点火角的控制及相电流组合实现总脉冲的调节^[6]。以往的研究通常集中在调波方法的定性分析上，较少涉及最优化问题。文献[6]以一台四相电机为研究对象，使用遗传算法对放点波形进行优化，但未能得到很好的结果。通过建立CPA放电数学模型，在放电仿真中可对电枢转子转速、励磁电流、点火角等参数进行灵活更改，结合智能优化算法，可以找到最优控制量组合，得到优化脉冲波形。本文以一台空心补偿脉冲发电机为对象，开展两相电机脉冲波形调节的最优化问题研究。

1. 补偿脉冲发电机放电数学模型

CPA的放电仿真方法多样，各有优缺点：场路耦合仿真方法将电机有限元模型和放电控制电路模型结合，开展联合仿真^[7]。这种方法计算准确，且能够得到电磁场分布情况，但是需要消耗大量计算资源，效率较低；将电机模型进行简化，例如将被动补偿CPA简化为电压源加电感、电阻的形式，在电路仿真软件中分析其放电特性^[8]。这种方法有一定局限性，对于等效电感随转子位置变化的情况不能有效模拟；建立放电过程的数学模型，通过解微分方程组的方法求解各物理量的变化。这种方法在建模阶段工作量较大，但精确的数学模型一旦建立，就能通过数值方法进行快速仿真，具有很强的灵活性^[6]。本文研究的波形调节最优化问题需要大量计算，故采取建立数学模型的方法实现放电仿真。

1.1 电机基本结构及工作原理

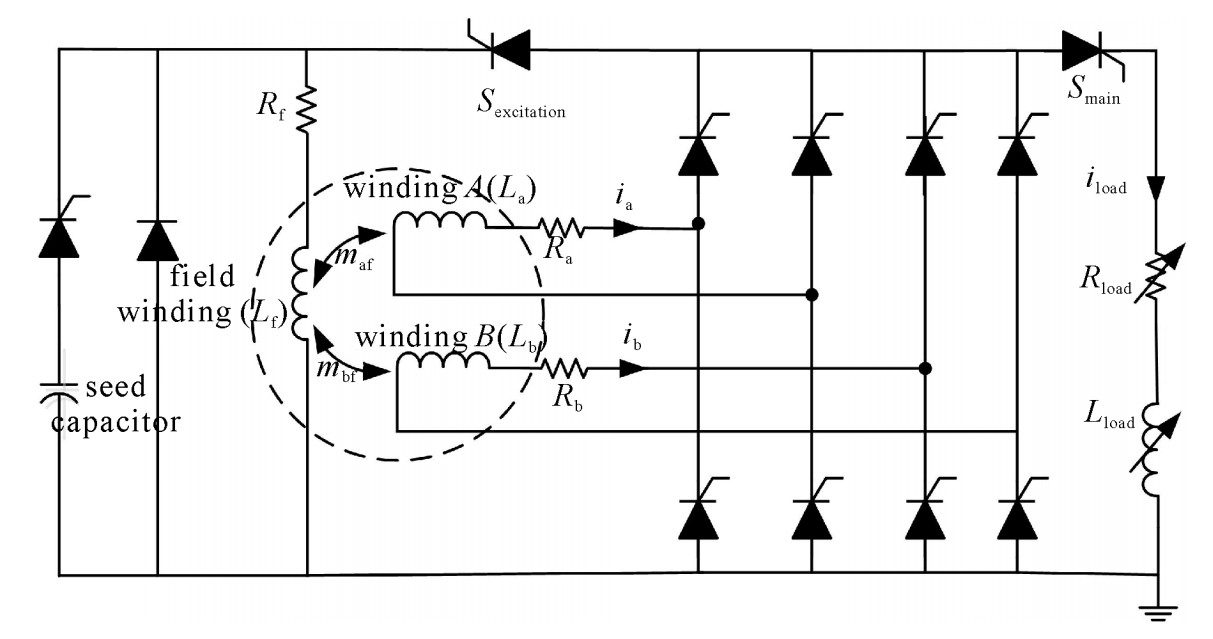
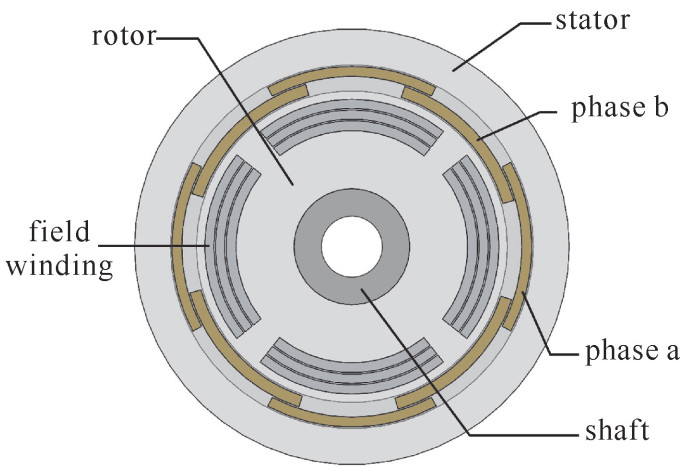
本文的两相四极空心CPA剖面如图 1所示，a，b两相电枢绕组正交放置，消除电磁耦合。不使用补偿屏蔽筒或补偿绕组等专门的补偿结构，放电工作时由励磁绕组实现补偿作用。

图 1 补偿脉冲发电机剖面图

Figure 1. Cross section of compulsator

下载: 全尺寸图片幻灯片

由于空心电机不使用铁磁材料，需要很强的励磁电流激励。为减轻系统质量，通常采用自励磁方法。自励磁及放电原理如图 2所示。先由一个电容器为励磁绕组充电，得到种子电流，随即将电枢绕组与励磁绕组连接，形成正反馈过程，励磁电流呈指数增大。当励磁电流达到要求时，打开放电主开关为负载供电。

图 2 自励磁及放电等效电路图

Figure 2. The equivalent circuit of excitation and discharge process

下载: 全尺寸图片幻灯片

1.2 放电数学模型

电流正方向以图 2标注为准，根据基尔霍夫定律可列写方程组

$\left\{\begin{array}{l} \frac{\mathrm{d} \psi_{\mathrm{a}}}{\mathrm{d} t}=i_{\mathrm{a}} R_{\mathrm{a}}+\left(i_{\mathrm{a}}+i_{\mathrm{b}}\right) R_{\text {load }}+\frac{\mathrm{d} L_{\text {load }}\left(i_{\mathrm{a}}+i_{\mathrm{b}}\right)}{\mathrm{d} t} \\ \frac{\mathrm{d} \psi_{\mathrm{b}}}{\mathrm{d} t}=i_{\mathrm{b}} R_{\mathrm{b}}+\left(i_{\mathrm{a}}+i_{\mathrm{b}}\right) R_{\text {load }}+\frac{\mathrm{d} L_{\text {load }}\left(i_{\mathrm{a}}+i_{\mathrm{b}}\right)}{\mathrm{d} t} \\ \frac{\mathrm{d} \psi_{\mathrm{f}}}{\mathrm{d} t}+i_{\mathrm{f}} R_{\mathrm{f}}=0 \\ i_{\text {load }}=\left|i_{\mathrm{a}}+i_{\mathrm{b}}\right| \quad \text { if: } \quad \operatorname{sign}\left(i_{\mathrm{a}} \cdot i_{\mathrm{b}}\right)>0 \end{array}, \quad\left\{\begin{array}{l} \frac{\mathrm{d} \psi_{\mathrm{a}}}{\mathrm{d} t}=i_{\mathrm{a}} R_{\mathrm{a}}+\left(i_{\mathrm{a}}-i_{\mathrm{b}}\right) R_{\text {load }}+\frac{\mathrm{d} L_{\text {load }}\left(i_{\mathrm{a}}-i_{\mathrm{b}}\right)}{\mathrm{d} t} \\ \frac{\mathrm{d} \psi_{\mathrm{b}}}{\mathrm{d} t}=i_{\mathrm{b}} R_{\mathrm{b}}-\left(i_{\mathrm{a}}-i_{\mathrm{b}}\right) R_{\text {load }}-\frac{\mathrm{d} L_{\text {load }}\left(i_{\mathrm{a}}-i_{\mathrm{b}}\right)}{\mathrm{d} t} \\ \frac{\mathrm{d} \psi_{\mathrm{f}}}{\mathrm{d} t}+i_{\mathrm{f}} R_{\mathrm{f}}=0 \\ i_{\text {load }}=\left|i_{\mathrm{a}}-i_{\mathrm{b}}\right| \quad \text { if: }: \quad \operatorname{sign}\left(i_{\mathrm{a}} \cdot i_{\mathrm{b}}\right)<0 \end{array}\right.\right.$

(1)

式中：ψ为磁链；i，R，L分别为电流、电阻、电感；下标a，b，f，load分别表示a, b两相电枢绕组、励磁绕组和负载；sign(·)为符号函数。

通过磁共能W_m可计算电磁转矩

$W_{\mathrm{m}}=\frac{1}{2}\left[\begin{array}{lll} -i_{\mathrm{a}} & -i_{\mathrm{b}} & i_{\mathrm{f}} \end{array}\right]\left[\begin{array}{ccc} L_{\mathrm{a}} & 0 & m_{\mathrm{af}} \\ 0 & L_{\mathrm{b}} & m_{\mathrm{bf}} \\ m_{\mathrm{af}} & m_{\mathrm{bf}} & L_{\mathrm{f}} \end{array}\right]\left[\begin{array}{c} -i_{\mathrm{a}} \\ -i_b \\ i_f \end{array}\right]$

(2)

式中：m_af，m_bf分别为a，b两相电枢绕组与励磁绕组的互感；L_f为励磁绕组的自感。

对四极电机，电磁转矩

$T=2 \partial W_{\mathrm{m}} / \partial \theta=2 i_{\mathrm{f}}\left(M_{\mathrm{af}} i_{\mathrm{a}} \sin \theta+M_{\mathrm{bf}} i_{\mathrm{b}} \cos \theta\right)$

(3)

式中：q为转子的电角度，本文中为机械角度的2倍；M_af，M_bf分别为互感m_af，m_bf在电机旋转过程中的最大值。

综合式(1)~(3)，经整理可写出完整的状态方程

$\left\{\begin{array}{l} p\left[\begin{array}{c} i_{\mathrm{a}} \\ i_{\mathrm{b}} \\ i_{\mathrm{f}} \end{array}\right]=\left[\begin{array}{ccc} -\left(L_{\mathrm{a}}+L_{\text {load }}\right) & -S L_{\text {load }} & m_{\mathrm{af}} \\ -S L_{\text {load }} & -\left(L_{\mathrm{b}}+L_{\text {load }}\right) & m_{\mathrm{bf}} \\ -m_{\mathrm{af}} & -m_{\mathrm{bf}} & L_{\mathrm{f}} \end{array}\right]^{-1}\left[\begin{array}{ccc} R_{\mathrm{a}}+R_{\text {load }}+\dot{L}_{\text {load }} & S\left(R_{\text {load }}+\dot{L}_{\text {load }}\right) & -\dot{m}_{\text {af }} \\ S\left(R_{\text {load }}+\dot{L}_{\text {load }}\right) & R_{\mathrm{b}}+R_{\text {load }}+\dot{L}_{\text {load }} & -\dot{m}_{\mathrm{bf}} \\ \dot{m}_{\mathrm{af}} & \dot{m}_{\mathrm{bf}} & -R_{\mathrm{f}} \end{array}\right]\left[\begin{array}{c} i_{\mathrm{a}} \\ i_{\mathrm{b}} \\ i_{\mathrm{f}} \end{array}\right] \\ \dot{\theta}=\omega, \quad \dot{\omega}=2 \frac{T}{J} \end{array}\right.$

(4)

式中：p表示微分算子；S=sign(i_a·i_b)； $\dot{m}_{\mathrm{af}}, \dot{m}_{\mathrm{bf}}$ 为互感的变化率； $\dot{L}_{\text {load }}$ 为负载电感变化率；J为转子的转动惯量； $\dot{\theta}=\omega$ ，为电角速度， $\dot{\omega}$ 为电角加速度。

2. 脉冲波形最优化方法

对于结构已经固定的CPA，只能通过外部控制调波，且控制量有限。但是电枢点火角、放电周期选择对单相脉冲影响很大，通过点火角控制以及多相脉冲组合是可以得到理想波形的。

本文讨论三种典型负载：电磁轨道炮、脉冲激光器和电热化学炮。这三种负载均可用CPA驱动，但它们的负载特性以及对脉冲波形的需求差异很大。因此，有必要对负载特性进行深入分析，进而研究CPA与负载的匹配问题。

2.1 电磁轨道炮

本文电磁轨道炮属于阻感负载，其电阻、电感值与弹丸位移成正比，弹丸所受电磁推力F与负载电流的平方成正比^[9]，即

$R_{\text {load }}=R^{\prime} x, \quad L_{\text {load }}=L^{\prime} x, \quad F=L^{\prime} i_{\text {load }}^2 / 2$

(5)

式中：L′，R′分别为电磁炮导轨的电感梯度和电阻梯度；x为弹丸位移。

电磁轨道炮的弹丸能够承受的最大过载(加速度)是有限制的。因此，在放电过程中尽量保持加速度均匀能够最大限度地加速弹丸，提高发射效率，达到最大炮口速度^[10]。为量化脉冲波形是否适用于电磁轨道炮，通常会计算放电过程平均加速度与峰值加速度的比值^[11]，本文简称为“加速度比”。设弹丸加速度为a，加速过程中最大加速度为a_max，放电起始和终止时间分别为t₀，t_f，则加速度比A_R的表达式为

$A_{\mathrm{R}}=\int_{t_0}^{t_{\mathrm{f}}} a(t) \mathrm{d} t /\left[a_{\max }\left(t_{\mathrm{f}}-t_0\right)\right]$

(6)

需要说明的是，加速度比与电流幅值无关，仅仅表征电流形状。加速度比越大，则说明波形越接近平顶波。设a，b两相电枢点火角分别为θ_a，θ_b，其组合决定了放电脉冲波形，加速度比也就随之确定，亦即加速度比是点火角的函数

$A_{\mathrm{R}}=A_{\mathrm{R}}\left(\theta_{\mathrm{a}}, \theta_{\mathrm{b}}\right)$

(7)

这样，CPA驱动电磁轨道炮的波形优化问题可转化为如下函数优化问题

$\left\{\begin{array}{l} \max A_{\mathrm{R}}\left(\theta_{\mathrm{a}}, \theta_{\mathrm{b}}\right) \\ \text { s. t. } \quad \theta_j^{\mathrm{L}} \leqslant \theta_j \leqslant \theta_j^{\mathrm{U}}, \quad j=\mathrm{a}, \mathrm{b} \end{array}\right.$

(8)

式中：θ_j^L，θ_j^U分别为点火角取值的上下界，由预先设定的放电周期决定。

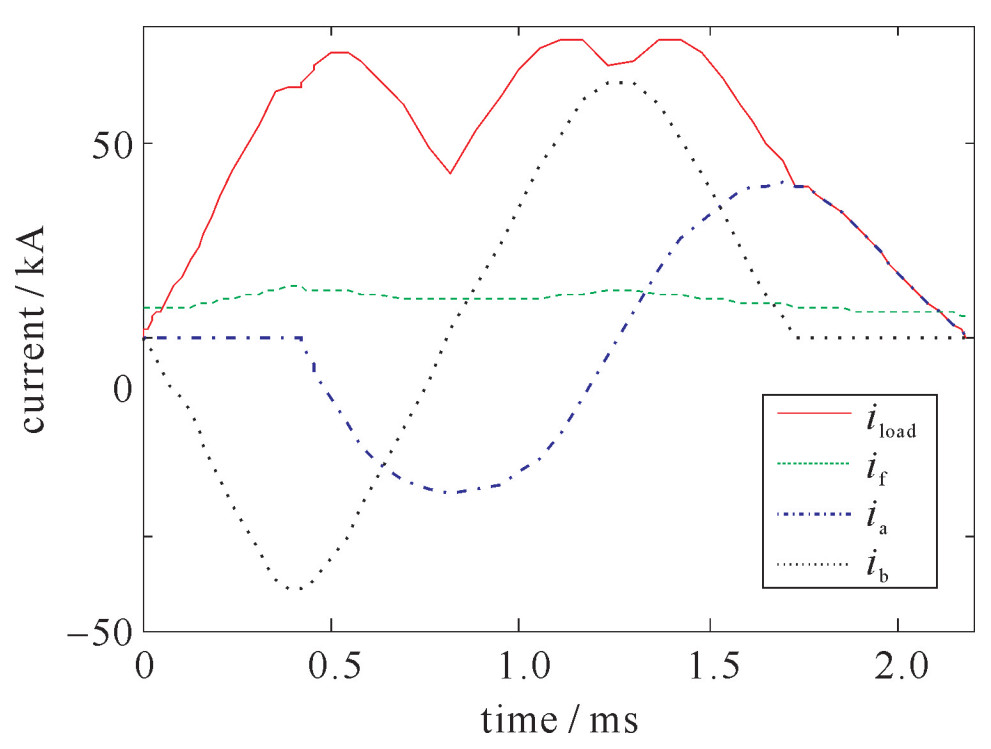
找到使加速度比最大的点火角组合，也就找到了最接近平顶脉冲、加速过程最平缓的放电波形。使用差分进化算法对该函数求最大值，仿真基本条件设置见表 1。令两相电枢各放电一个周期，优化后的波形如图 3所示，优化结果为：[q_a, q_b]=[1.546, 1.571]，A_R=0.513。根据优化结果可知，当两相点火角在π/2附近时，合成后的波形最接近平顶脉冲。

表 1 仿真参数设置

Table 1. Simulation parameters

initial rotor speed/(r·min^-1)	initial field current/kA	rotor’s moment of inertia/(kg·m²)	mass of projectile/g	inductance gradient/(μH·m^-1)	resistance gradient/(mΩ·m^-1)	discharge period
18 000	8	0.177 5	5	1	0.5	1

下载: 导出CSV

| 显示表格

图 3 电磁轨道炮优化放电波形

Figure 3. Optimized discharge pulse for EM gun

下载: 全尺寸图片幻灯片

2.2 脉冲激光器

本文电磁轨脉冲激光器是一种非线性电阻性负载，阻值在整个放电过程中呈先下降再上升的U型曲线^[12]，稳定放电时，有^[13]

$R_{\text {load }}=K_0 / \sqrt{i_{\text {load }}}$

(9)

式中：K₀是脉冲氙灯的阻抗系数，与其物理结构有关。

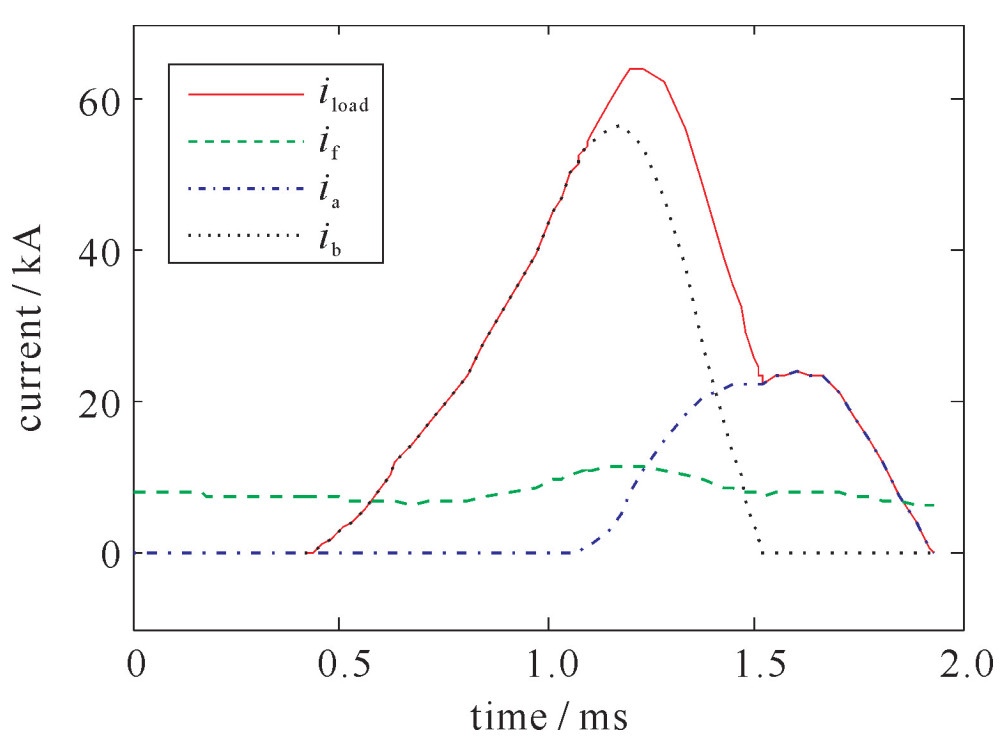
脉冲激光器需要尖顶脉冲驱动。虽然没有弹丸加速过程，但同样可使用“加速度比”的概念来量化波形效果，求解加速度比最小值即可。设阻抗系数K₀=5时，优化结果为：[q_a, q_b]=[4.015, 3.142]，A_R=0.293。优化后的波形如图 4所示，可见，将加速度比的计算方法应用于脉冲激光器的脉冲优化是可行的，能够得到尖顶脉冲。

图 4 脉冲激光器优化放电波形

Figure 4. Optimized discharge pulse for flashlamp

下载: 全尺寸图片幻灯片

2.3 电热化学跑

电热化学炮的核心部件为毛细管，也可以看作非线性电阻。本文使用文献[14]建立的物理模型表示

$R_{\text {load }}=0.22 l \beta^{8 / 11} \alpha^{-13 / 11} i_{\text {load }}^{-6 / 11}$

(10)

式中：l为毛细管长度，β为比例常数，α为毛细管截面半径。

电热化学炮所需波形是分段上升的，很难找出一个简单的计算量来表征其优劣。文献[15]电热炮对电流的要求，即

$i_{\text {desire }}(t)=\frac{1}{2} p_0 A \sqrt{\frac{1}{m(\gamma-1)}} \sqrt{\frac{t}{R_{\text {load }}}}$

(11)

式中：i_desire表示需求电流，p₀为炮膛加速压力，A为炮膛截面积，m为弹丸质量，γ为气体绝热常数。

电流幅值可以通过励磁电流大小、转速等调节。为消除幅值影响，表征实际电流与需要电流波形的匹配程度，本文提出“形状方差”的概念，计算方法如下。

(1) 设定点火角，计算实际放电电流i_load(t)= i_load(q_a, q_b)，R_load(t)=R_load(q_a, q_b)。根据式(10)~(11)计算需求放电电流i_desire(t)，其中，t₁，t_k分别对应放电初始时刻和结束时刻。

(2) 将放电时间适当离散化，取k个时间点：t′=[t₁, t₂, t₃, …, t_k]。其中，t₁，t_k分别对应放电初始时刻和结束时刻。

(3) 求出各时间点处实际电流i_load(t_k)与需求电流i_desire(t_k)的比值，虚拟的统计量

$R_{\text {ld }}(k)=i_{\text {load }}\left(t_k\right) / i_{\text {desire }}\left(t_k\right)$

(12)

(4) 计算电流比值的方差，定义为“形状方差”S_V，可表示为

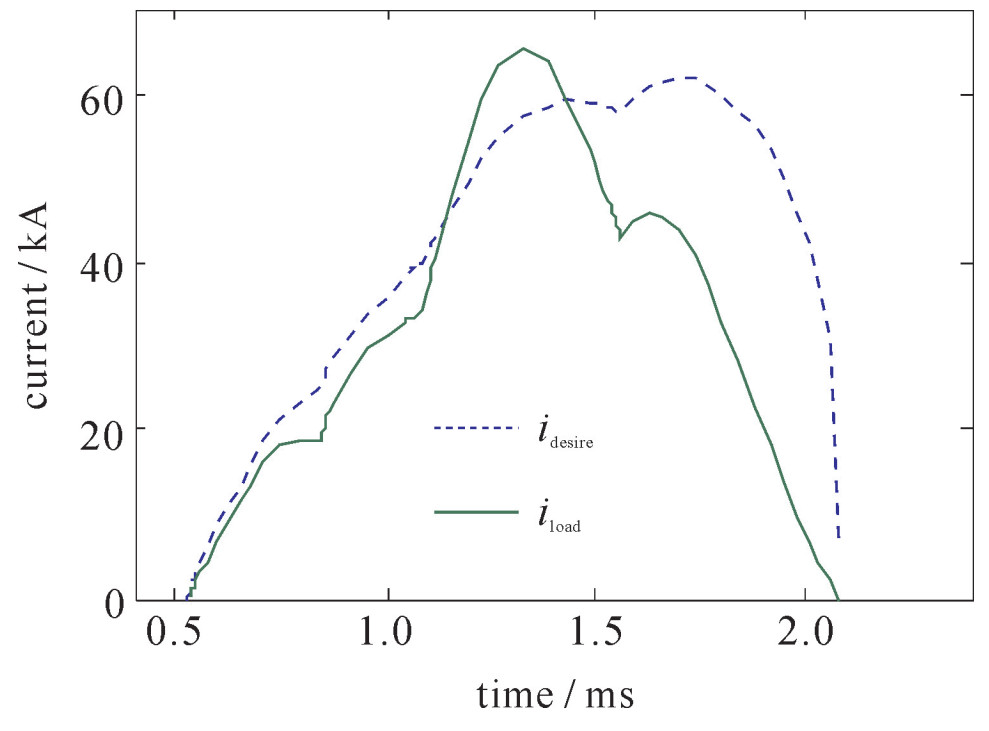
$S_V=\operatorname{var}\left(R_{\text {ld }}\right)$

(13)

这样，得到的形状方差能够描述实际电流与需求电流形状的匹配程度。在相同的初始励磁电流、转速等条件下，形状方差越小，说明波形越符合要求。优化结果为：[q_a, q_b]=[2.005, 4.712]。优化的放电波形如图 5所示，图 6显示了需求电流与实际电流的对比情况。可见，实际电流与需求电流有一定差别，但基本符合电热化学炮的要求。

图 5 电热化学炮优化放电波形

Figure 5. Optimized discharge pulse for ETC

下载: 全尺寸图片幻灯片

图 6 需求电流与实际电流对比

Figure 6. Comparison of desired and actual current

下载: 全尺寸图片幻灯片

3. 结论

本文建立了两相空心补偿脉冲发电机放电过程的数学模型，在此基础上开展了放电模型最优化研究。针对三种不同负载，分析负载特性及需求波形，提出相应的优化指标。优化结果表明，采用加速度比作为优化指标，可以有效得到适合电磁轨道炮和脉冲激光器的放电脉冲。对于电热化学炮，本文定义的“形状方差”可较好地对放电脉冲进行优化。基于电机数学模型的仿真具有很高的灵活性。但是，文中建立的数学模型是否准确，提出的波形优化方法是否合理，则需要进一步的实验验证。根据实验结果对仿真模型进行修正，可以得到更加精确的模型。两相电机具有较强的波形调节能力。可以推论，随着相数进一步增加，电机放电波形调节的灵活性将进一步增强。

图 1 补偿脉冲发电机剖面图

Figure 1. Cross section of compulsator

下载: 全尺寸图片幻灯片

图 2 自励磁及放电等效电路图

Figure 2. The equivalent circuit of excitation and discharge process

下载: 全尺寸图片幻灯片

图 3 电磁轨道炮优化放电波形

Figure 3. Optimized discharge pulse for EM gun

下载: 全尺寸图片幻灯片

图 4 脉冲激光器优化放电波形

Figure 4. Optimized discharge pulse for flashlamp

下载: 全尺寸图片幻灯片

图 5 电热化学炮优化放电波形

Figure 5. Optimized discharge pulse for ETC

下载: 全尺寸图片幻灯片

图 6 需求电流与实际电流对比

Figure 6. Comparison of desired and actual current

下载: 全尺寸图片幻灯片

表 1 仿真参数设置

Table 1. Simulation parameters

initial rotor speed/(r·min^-1)	initial field current/kA	rotor’s moment of inertia/(kg·m²)	mass of projectile/g	inductance gradient/(μH·m^-1)	resistance gradient/(mΩ·m^-1)	discharge period
18 000	8	0.177 5	5	1	0.5	1

下载: 导出CSV

参考文献(15)

[1]	McNab I R. Pulsed power options for large EM launchers[J]. IEEE Trans Plasma Sci, 2015, 43(5): 1352-1357. doi: 10.1109/TPS.2014.2372173
[2]	Dai Ling, Dong Hanbin, Lin Fuchang, et al. Miniaturization of thyristor applied in pulse power supply[J]. Trans of China Electrotechnical Society, 2012, 27(8): 120-125.
[3]	Tang Lei, Yu Kexun. Investigation of the transient inductance for a pulsed alternator with fully passive compensation[J]. IEEE Trans Plasma Sci, 2016, 44(1): 71-78. doi: 10.1109/TPS.2015.2507399
[4]	Herbst J, Beno J, Ouroua A, et al. High slew rate power supplies for support of large pulsed loads[C]//IEEE Electric Ship Technologies Symposium (ESTS). 2015: 446-452.
[5]	Driga M D, Pratap S B, Weldon W F. Design of compensated pulsed alternators with current waveform flexibility[C]//6th IEEE Pulsed Power Conference. 1987.
[6]	Gao Liang, Li Zhenxiao, Li Baoming. The modeling and calculation on an air-core passive compulsator[J]. IEEE Trans Plasma Sci, 2015, 43(3): 864-868. doi: 10.1109/TPS.2015.2394352
[7]	Cui S M, Zhao W D, Wang S F, et al. Investigation of multiphase compulsator systems using a Co-simulation method of FEM-circuit analysis[J]. IEEE Transactions on Plasma Science, 2013, 41(5): 1247-1253. doi: 10.1109/TPS.2013.2248389
[8]	王昊泽. 基于磁悬浮飞轮储能的被动补偿脉冲发电系统研究[D]. 长沙: 国防科学技术大学, 2010. Wang Haoze. Study on the compulsator system based on magnetic suspension flywheel. Changsha: National University of Defense Technology, 2010
[9]	朱博峰, 鲁军勇, 王杰. 轻小型脉冲电源驱动的电磁发射系统建模[J]. 海军工程大学学报, 2016, 28(3): 100-104. https://www.cnki.com.cn/Article/CJFDTOTAL-HJGX2016S1021.htm Zhu Bofeng, Lu Junyong, Wang Jie. Modeling of electromagnetic launch system driven by CPA. Journal of Naval University of Engineering, 2016, 28(3): 100-104 https://www.cnki.com.cn/Article/CJFDTOTAL-HJGX2016S1021.htm
[10]	Pratap S B, Driga M D, Weldon W F, et al. Future trends for compulsators driving railguns[J]. IEEE Trans Magn, 1986, 22(6): 1681-1683. doi: 10.1109/TMAG.1986.1064680
[11]	Pratap S B, Hsieh K T, Driga M D, et al. Advanced compulsators for railguns[J]. IEEE Trans Magnetics, 1989, 25(1): 454-459. doi: 10.1109/20.22581
[12]	陈佳, 李海兵, 蒋宝财, 等. 脉冲氙灯放电时等离子体电阻的研究[J]. 激光与红外, 2009, 39(2): 190-193. doi: 10.3969/j.issn.1001-5078.2009.02.019 Chen Jia, Li Haibing, Jiang Baocai, et al. Research on the impedance of plasma in xenon flash lamp during discharging. Laser and Infrared, 2009, 39(2): 190-193 doi: 10.3969/j.issn.1001-5078.2009.02.019
[13]	Winstanley P A. The role of pulse power in flashlamp pumped lasers[C]//IEE Colloq on Pulsed Power. 1997.
[14]	Loeb A, Kaplan Z. A theoretical model for the physical processes in the confined high pressure discharges of electrothermal launchers[J]. IEEE Trans Magn, 25(1): 342-346. doi: 10.1109/20.22561
[15]	Driga M D, Ingram M W, Weldon W F. Electrothermal accelerators: the power conditioning point of view[J]. IEEE Trans Magnetics, 25(1): 147-152. doi: 10.1109/20.22524

施引文献

期刊类型引用(2)

1.	张鹏，李海涛，胡长勇，孔令硕. 空心脉冲发电机剩磁能量回收方法. 强激光与粒子束. 2023(11): 118-125 . 本站查看
2.	王勇，黄军高，管荑，马强，李雷. 具有脉冲负载波动的电力系统稳定性分析. 信息技术. 2020(06): 114-120 . 百度学术

其他类型引用(3)

资源附件(0)

访问统计

点击查看大图

图(6) / 表(1)

计量

文章访问数: 1223
HTML全文浏览量: 288
PDF下载量: 108
被引次数: 5

1. 补偿脉冲发电机放电数学模型
1.1 电机基本结构及工作原理
1.2 放电数学模型
2. 脉冲波形最优化方法
2.1 电磁轨道炮
2.2 脉冲激光器
2.3 电热化学跑
3. 结论

姓名
邮箱
手机号码
标题
留言内容
验证码

留言板

补偿脉冲发电机放电波形优化方法

doi: 10.11884/HPLPB201830.170325

作者简介:
陶雪峰(1992－)，男，硕士，从事惯性储能脉冲功率技术研究；taoxuefeng11@sina.cn

计量

Pulse shaping method for compulsator

1. 补偿脉冲发电机放电数学模型

1.1 电机基本结构及工作原理

1.2 放电数学模型

2. 脉冲波形最优化方法

2.1 电磁轨道炮

2.2 脉冲激光器

2.3 电热化学跑

3. 结论

期刊类型引用(2)

其他类型引用(3)

计量

目录

1. 补偿脉冲发电机放电数学模型

1.1 电机基本结构及工作原理

1.2 放电数学模型

2. 脉冲波形最优化方法

2.1 电磁轨道炮

2.2 脉冲激光器

2.3 电热化学跑

3. 结论

留言板

补偿脉冲发电机放电波形优化方法

doi: 10.11884/HPLPB201830.170325

作者简介: 陶雪峰(1992－)，男，硕士，从事惯性储能脉冲功率技术研究；taoxuefeng11@sina.cn

计量

出版历程

Pulse shaping method for compulsator

1. 补偿脉冲发电机放电数学模型

1.1 电机基本结构及工作原理

1.2 放电数学模型

2. 脉冲波形最优化方法

2.1 电磁轨道炮

2.2 脉冲激光器

2.3 电热化学跑

3. 结论

期刊类型引用(2)

其他类型引用(3)

计量

出版历程

目录

1. 补偿脉冲发电机放电数学模型

1.1 电机基本结构及工作原理

1.2 放电数学模型

2. 脉冲波形最优化方法

2.1 电磁轨道炮

2.2 脉冲激光器

2.3 电热化学跑

3. 结论

作者简介:
陶雪峰(1992－)，男，硕士，从事惯性储能脉冲功率技术研究；taoxuefeng11@sina.cn