Optimization of PFN-Marx generator
-
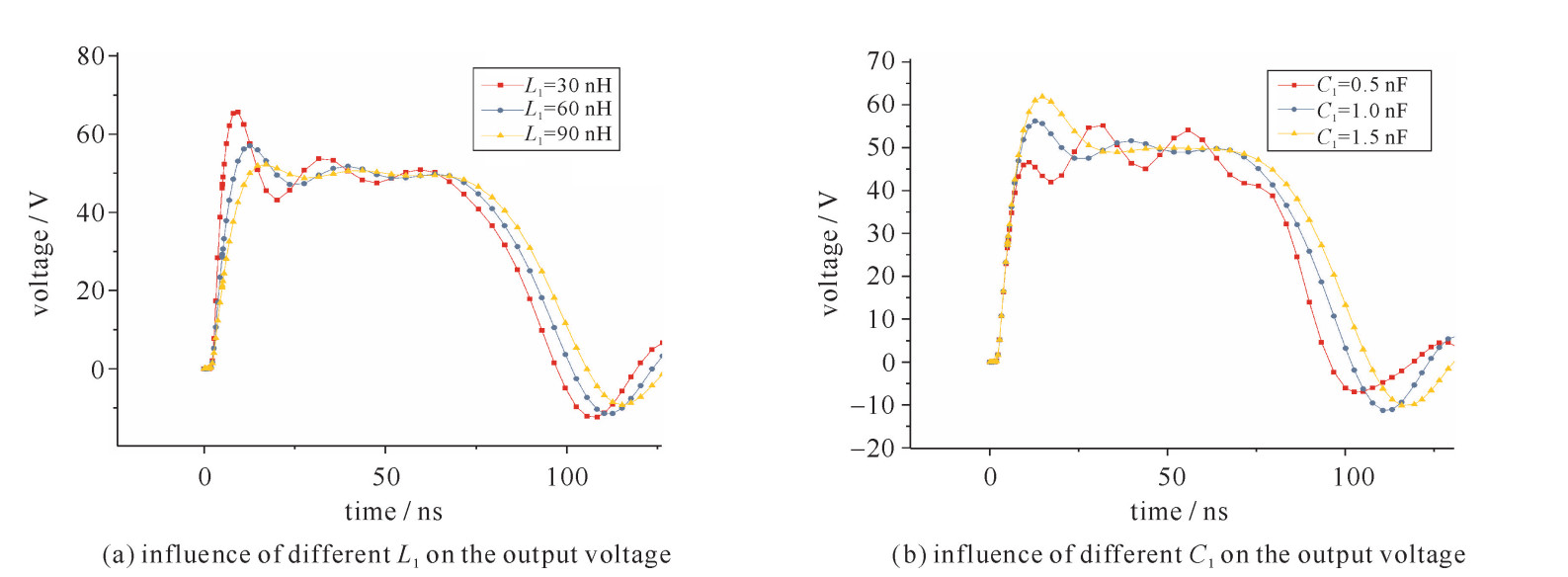
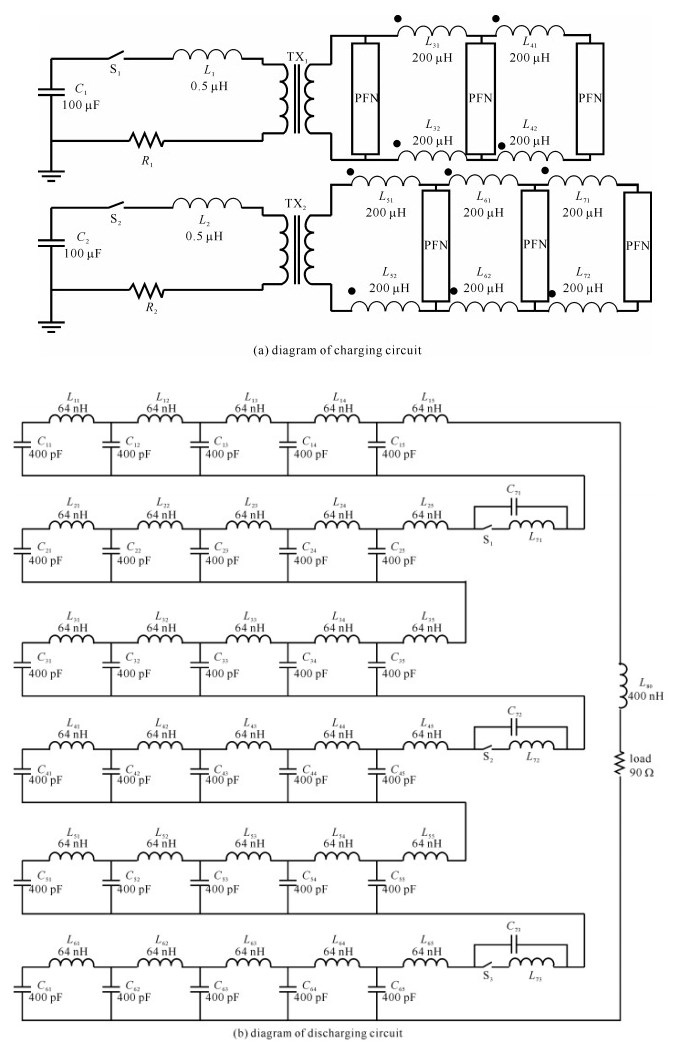
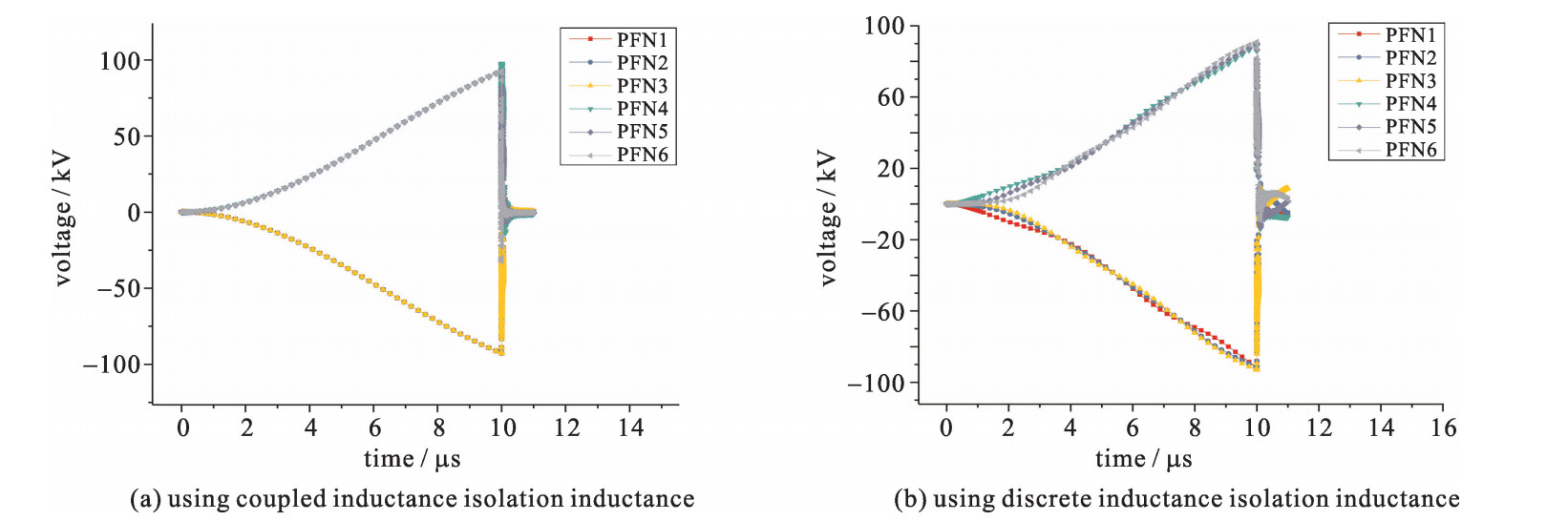
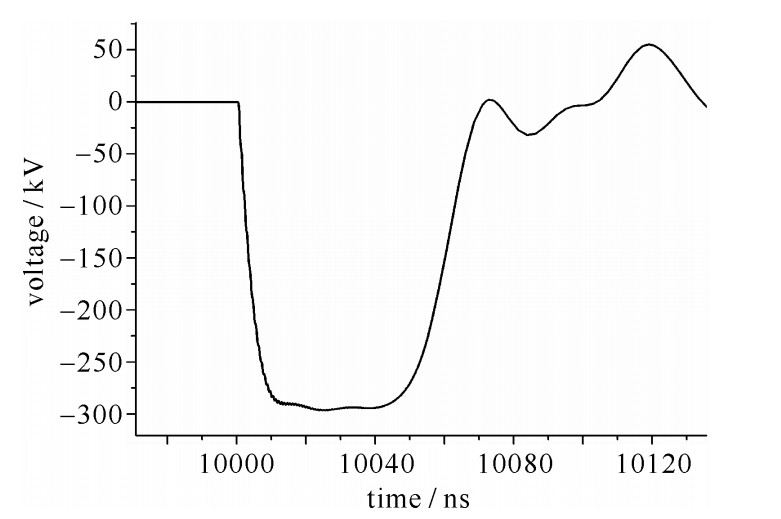
摘要: 为了改善脉冲形成网络(PFN)-Marx发生器的输出波形,得到前沿较短、纹波因数尽可能小的输出波形,对单级PFN的特性进了仿真研究,包括PFN中末端电容、末端电感、PFN的阻抗等因素对单级PFN的输出波形的影响;建立了PFN-Marx发生器的整体仿真模型,并对采用耦合电感作为隔离电感和采用分立电感作为隔离电感进行了仿真研究。研究表明:采用耦合电感作为隔离电感可以使各级PFN的充电波形更加一致,效果更好。搭建了一个小型的PFN-Marx发生器,并研究了PFN-Marx发生器中气体开关在不同气压下导通时输出波形的差异,结果表明,升高气压有利于减小PFN-Marx发生器输出波形的前沿持续时间。
-
关键词:
- 脉冲发生器 /
- PFN-Marx发生器 /
- 仿真 /
- 方波
Abstract: This paper aims to improve the output waveform of pulse forming network (PFN) -Marx generator and get output waveform of short rise time and small ripple factor. Firstly, characteristics of the single stage PFN are studied by simulation, including the impact of single stage PFN terminal capacitance, inductance and PFN terminal impedance on output waveform. The complete simulation model of PFN-Marx generator is established. Using coupled inductor as isolating inductor and using discrete inductor as isolation inductor are studied. The simulation result shows that using coupled inductor as isolating inductor can make charging waveform of PFN more consistent. A small PFN-Marx generator is built. The difference of output waveform of gas switch in PFN-Marx generator under different atmospheric pressure is studied. The result shows that increasing air pressure is beneficial to decrease the rise time of output waveform of PFN-Marx generator.-
Key words:
- pulse transformer /
- PFN-Marx generator /
- simulation /
- square wave
-
在X光闪光照相实验中[1-6],光源的尺寸及分布是影响成像质量的一个主要因素。光源点扩展函数的半高全宽(FWHM)作为一种描述焦斑尺寸的常用参数,多年来一直是表征光源性能的关键指标[7]。而近些年来,随着闪光照相技术的持续发展和对图像分辨率要求的不断提升,仅靠FWHM来描述光源的空间分辨率有其固有的局限,相关成像实验发现,如果光源点扩展函数不同,即使其FWHM相同,图像的分辨情况也会不同,因为束流分布的底宽也会对成像质量造成影响,为了充分考虑这一因素,美国LANL提出利用空间频域50%的调制传递函数(MTF)来评价光源尺寸[8-9],该参数也将成为下一步光源底宽优化的重要评价指标。
高剂量X光源通常来自高能电子束轰击高Z靶材产生的轫致辐射,光源分布很大程度上取决于击靶电子束的焦斑分布[10],优化电子束的焦斑分布是改善光源分布的重要手段。本文通过研究一台直线感应加速器中电子束的聚焦过程,着重分析束流上升/下降沿能量、流强不一致性等对束流焦斑FWHM与MTF尺寸的影响,为束流焦斑的进一步优化提供理论基础。考虑到直线感应加速器中电子束长度达到约30 m(持续时间约100 ns),全束流模拟需要大量计算资源,往往难以实现,本文将高能(约18 MeV)电子束流分割成约1.1 ns的束片,通过动态网格的PIC代码[11](含束流自身电磁力)模拟逐束片的聚焦过程,然后叠加形成最终束流分布。
1. 束斑尺寸描述方法简介型
这里以常用的光斑尺寸描述方法来描述电子束打靶焦斑,设电子束的横向分布函数为
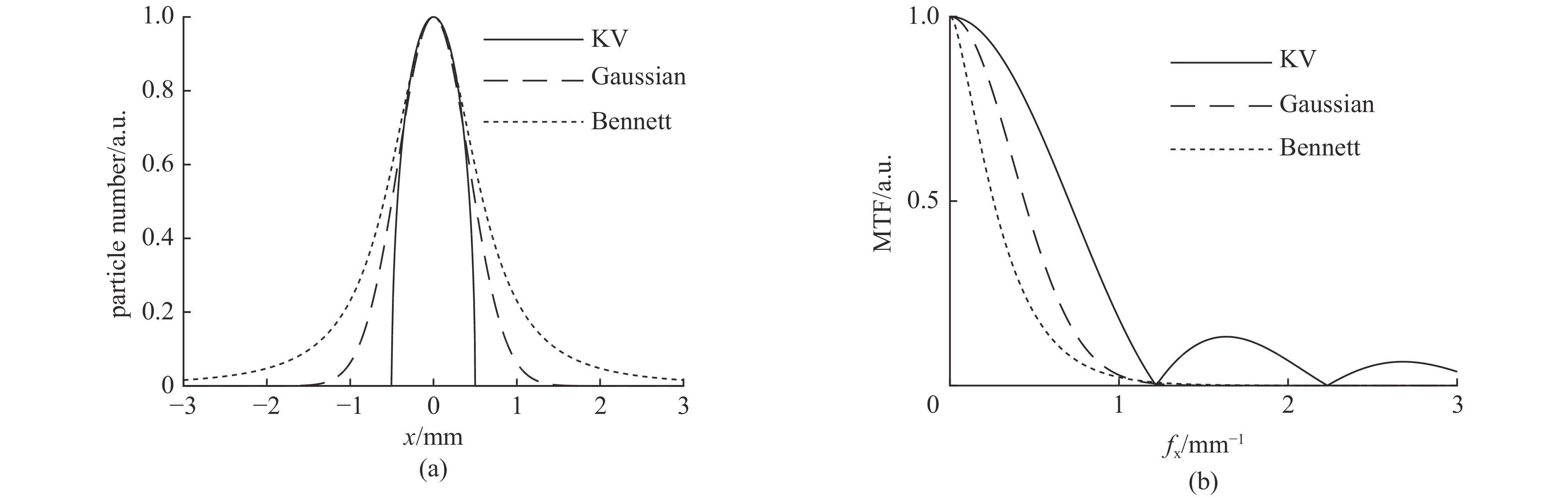
f(x,y) ,则其对应的线扩展函数fL(x)=∫f(x,y)dy ,点扩展函数为fs(x)=f(x,0) 。FWHM尺寸指其点扩展函数fs 的半高全宽,记fs(x) 的最大值为fs.max ,且有fs(x1)=fs(x2)=0.5fs.max ,则束流的FWHM尺寸为|x2−x1| ,该参数主要反映有效应用区域的尺寸,是实验中常用的评价指标。调制传递函数(MTF)等效均匀分布尺寸描述线扩展函数fL(x) 的空间频域特性,设线扩展函数fL(x) 的傅里叶变换为F(k),且有F(k0)=0.5max(F(k)) ,则束流的MTF尺寸为0.705/k0 (0.705为均匀圆盘分布情况下k0 与半高全宽的乘积),该参数对于分布的底宽较为敏感。直线感应加速器中常用的束流分布表征函数有均匀分布(KV)、高斯分布(Gaussian)和本涅特(Bennett)分布,在相同的FWHM时,三种分布的底宽和MTF焦斑依次增大,其分布曲线(线扩展函数)及对应的空间频域曲线如图1所示。在三种分布函数下,FWHM尺寸
σFWHM 和MTF尺寸σMTF 有线性对应关系,如表1所示。均匀布时σMTF/σFWHM=1 ,高斯分布和本涅特分布的底宽依次增大,σMTF/σFWHM 分别为1.6和2.7,可见σMTF/σFWHM 值与分布底宽呈正相关,后文的分析中将通过σMTF/σFWHM 来判断束流的分布及其底宽特征。表 1 不同分布函数下,FWHM尺寸与MTF尺寸的对应关系Table 1. Relationship between the FWHM beam size and the MTF beam size in various distributionsf(x) σFWHM/mm k0/mm−1 σMTF/mm KV 1.00 0.705 1.00 Gaussian 1.00 0.441 1.60 Bennett 1.00 0.258 2.70 2. 能散对束流聚焦影响
2.1 束流聚焦的理论分析
忽略空间电荷效应以及透镜像差,单能电子束在聚焦平面处的均方根尺寸主要受限于束流发射度,近似表示为
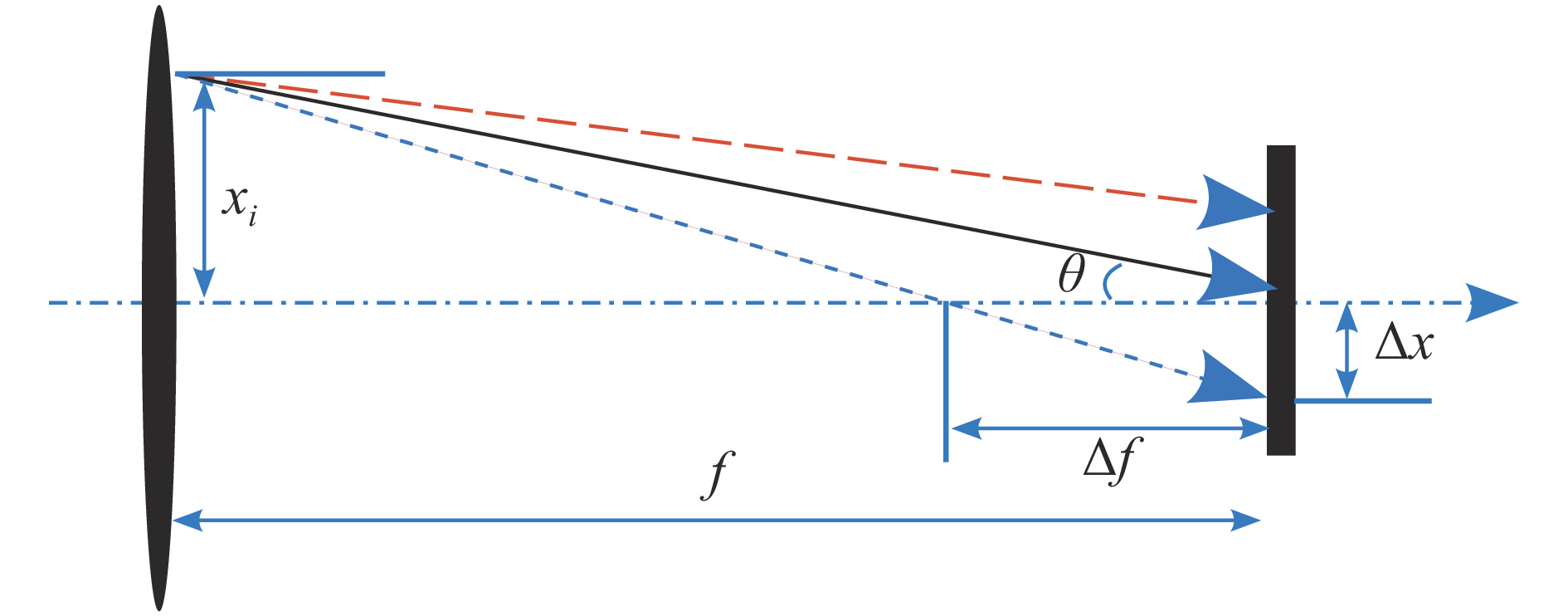
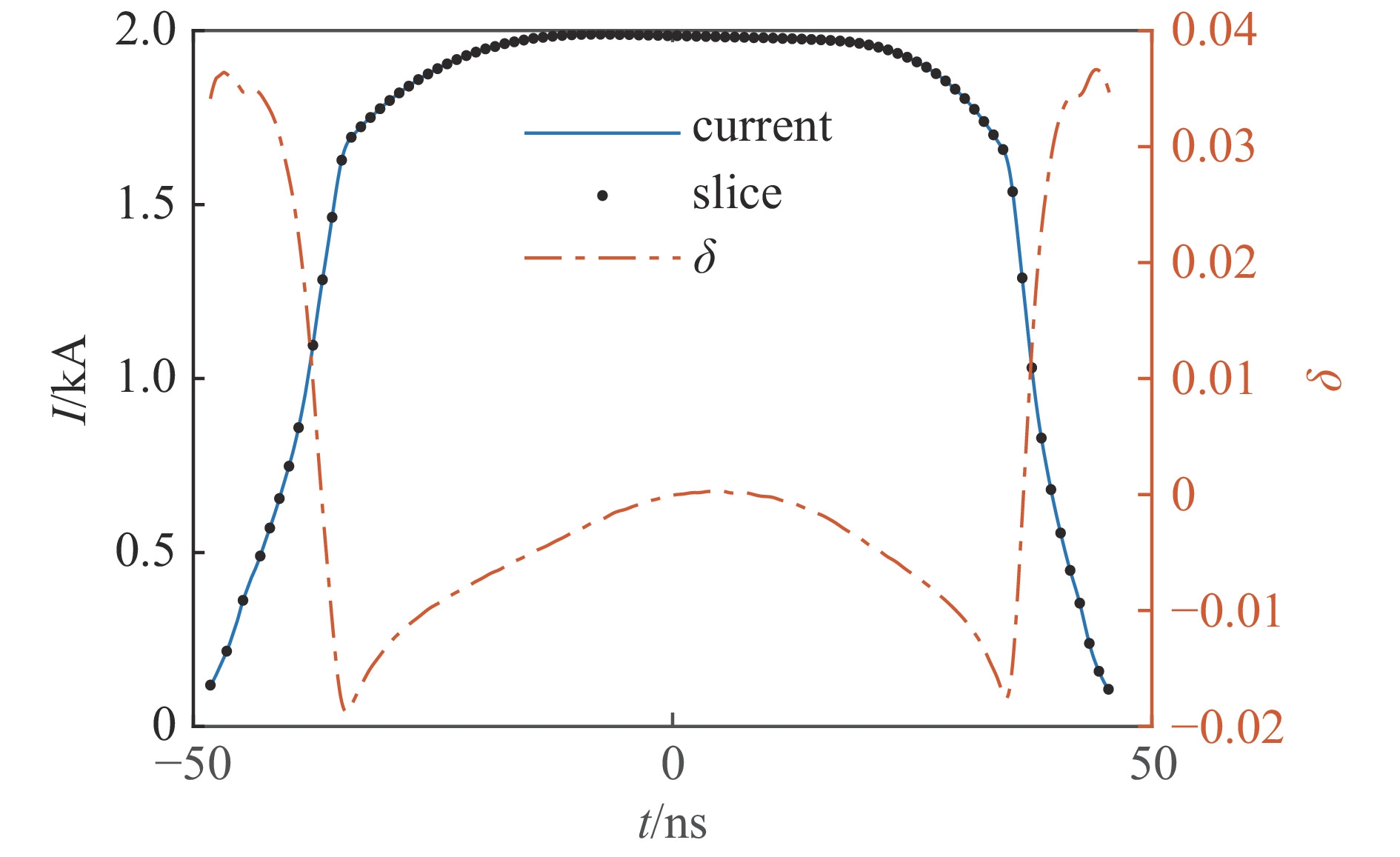
σf.ϵ=fϵx/σi ,其中f、σi、ϵx 分别为焦距,束流初始均方根半径及发射度[12]。焦距与电子束的能量正相关即f∝p0 (p0 为参考电子的能量),一个能量为p 的电子与参考电子的相对能量差异为δ=(p−p0)/p0 ,经过聚焦线圈后焦距差异为Δf=fδ ,如图2所示。一般而言,电磁透镜的焦距远大于焦斑尺寸,则根据图2易得初始位置为xi 、相对能量差异为δ 的电子在焦点处的横向位置为Δx≈Δfθ =fxiδ ,则受能散限制的焦斑尺寸可近似表示为σf.δ=σiσδ ,其中σi 和σδ 分别为束流的均方根半径和均方根能散,即xi 和δ 的均方根值。由于能散与发射度的影响相互独立,最终焦斑尺寸可以表示为σf=√f2ϵ2x/σ2i+σ2iσ2δ (1) 公式(1)的推导中忽略了束流聚焦前后发射度变化,这在横向非线性力较弱时对于薄束片而言是适用的。以一组实验参数作为计算输入条件:束流的能散分布由加速腔腔压叠加并考虑束流负载效应后获得,中心束片能量17 MeV,如图3虚线所示,流强波形通过B-dot测量获得如图3实线所示,切片发射度
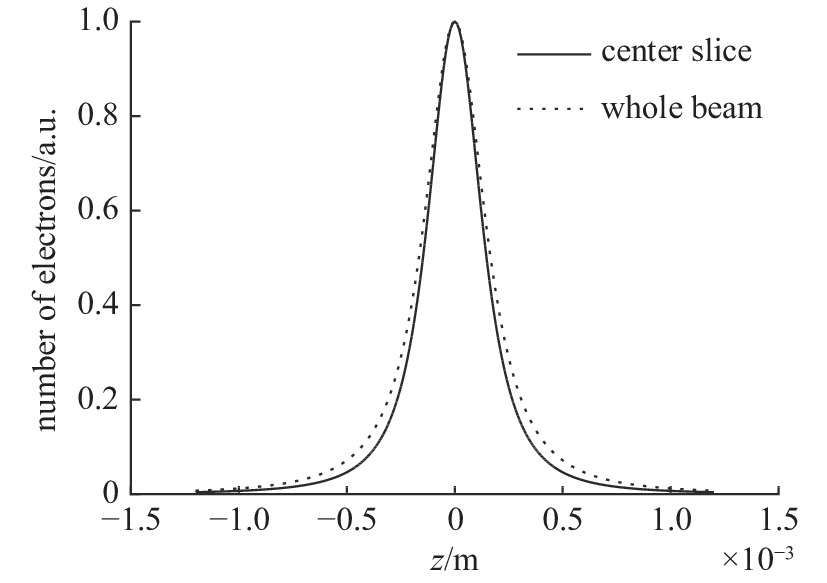
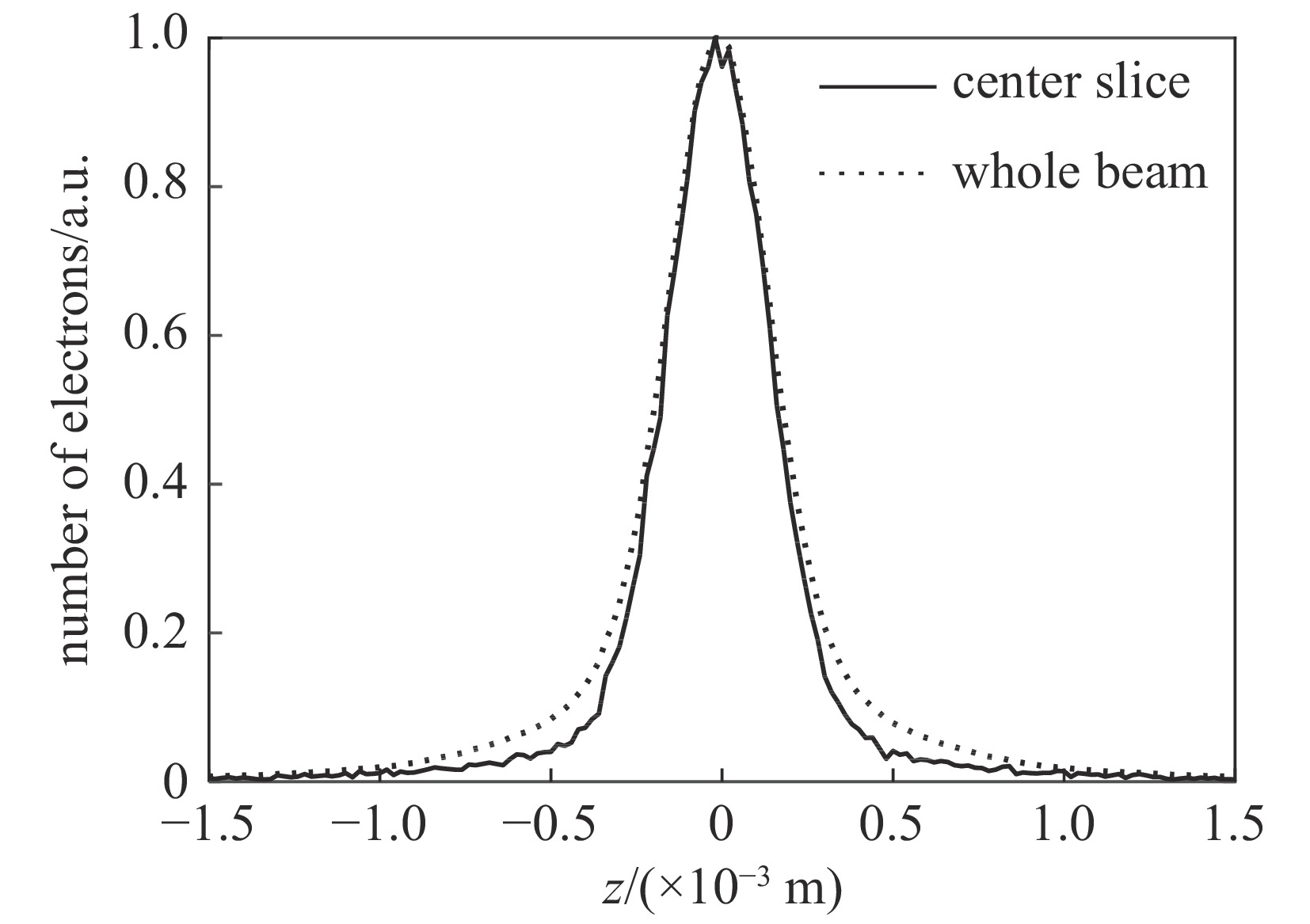
ϵx.slice=200 µm,束流聚焦前尺寸σi=10mm ,根据螺线管磁场求得中心束片的焦距f=1/∫e2B2z/(2mcβγ)2dz=209mm ,其中m,e分别为电子的质量和电荷量,Bz 为聚焦磁场强度,β 为电子经光速归一化的速度,γ 为洛伦兹系数,z为轴向坐标变量。将图3所示束流分为91个1.1 ns的切片(从左到右依次编号,中心束片为#46),将其能量差分别代入公式(1)可估算逐束片聚焦后的均方根尺寸。假设聚焦后单束片呈高斯分布,将束片分布按权重叠加即可得到聚焦后整个束流的横向分布,束片权重为其归一化电荷量。根据公式(1)计算得到的中心束片(#46)及整个束流(#1-#91束片叠加)的焦斑分布如图4所示,中心束片以实线表示,整个束流以虚线表示,可见整个束流的底宽明显大于中心束片,但是半高宽差异并不明显。
将中心束片聚焦后的MTF和FWHM尺寸分别记为
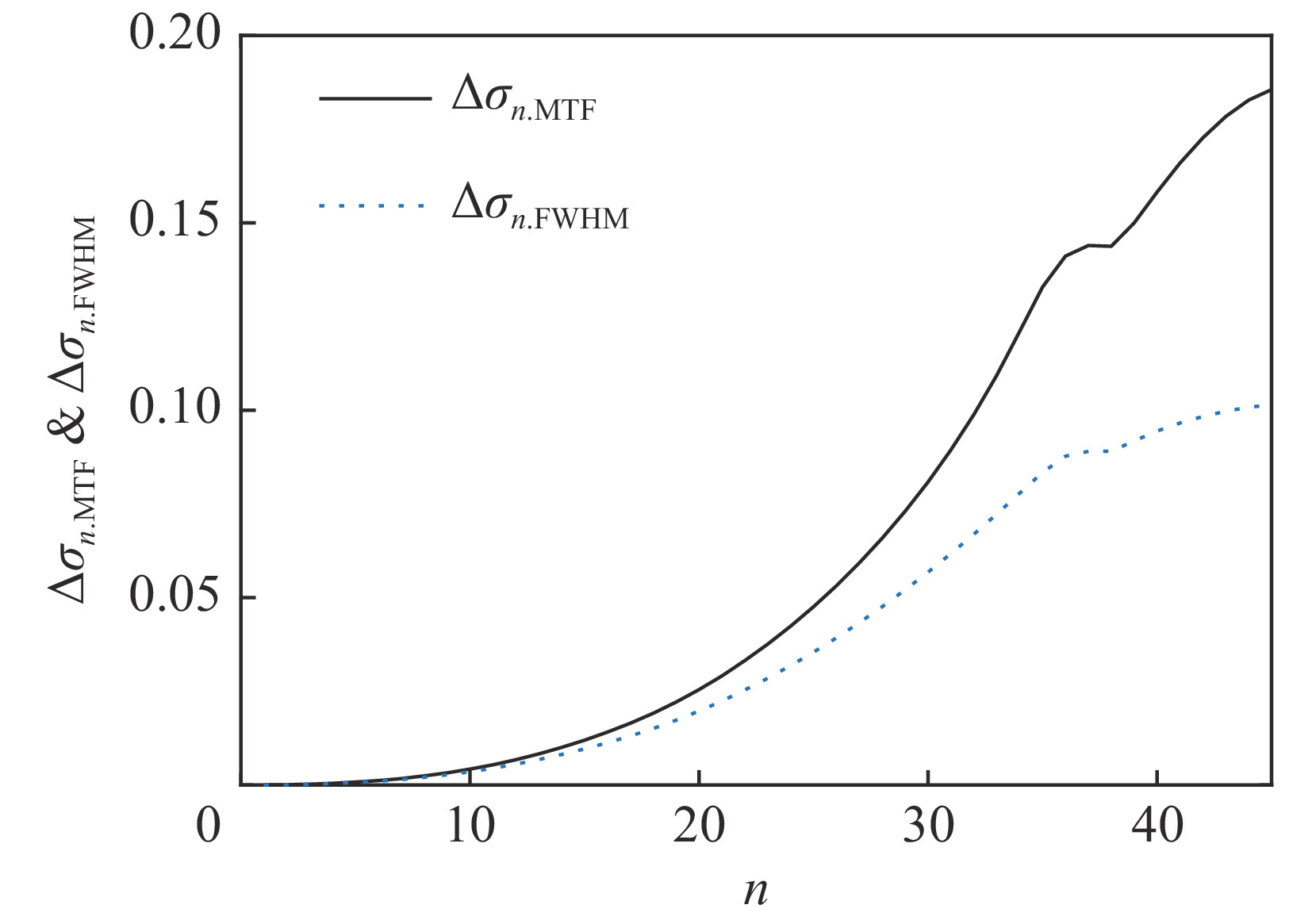
σ0.MTF 和σ0.FWHM ,将#(46-n)号束片至#(46+n)号束片聚焦后叠加分布的MTF和FWHM尺寸分别记为σn.MTF 和σn.FWHM 。根据计算结果可得在焦点位置处σ0.MTF=0.46mm ,σ0.FWHM=0.29mm ,为了分析上升/下降沿叠加后对束流尺寸、分布的影响,进一步计算了n分别取值1~45时叠加分布的MTF/FWHM尺寸相对于中心束片的增长量,将相对增长量表示为Δσn.MTF 和Δσn.FWHM ,其中Δσn.MTF=(σn.MTF−σ0.MTF)/σ0.MTF ,Δσn.FWHM=(σn.FWHM−σ0.FWHM)/σ0.FWHM ,计算结果如图5所示。可见上升/下降沿束片的叠加使得束流绝对尺寸逐渐增大,但MTF尺寸的增长幅度明显高于FWHM尺寸,即Δσn.MTF/Δσn.FWHM 比值随n增大,束流底宽随n的增大逐渐增长。全束流的MTF/FWHM尺寸与中心束片相比分别增长了约18.6%/10.1%,单束片呈高斯分布有σ0.MTF/σ0.FWHM=1.60 ,而全束片叠加后的MTF尺寸与FWHM尺寸比值增长至1.73,对比表1数据可知,全束流分布介于高斯分布和本涅特分布之间。上述估算中束片间的唯一差异为能量,可见减小束流能散可以有效的控制束流底宽,减小束流的MTF尺寸。但是由于中间束片的电荷量较大,而上升/下降沿束片电荷量小,束片内的空间电荷力并不一致,因此对束片内分布的影响也不一致,定量评估能散/流强对束流聚焦后尺寸影响需要考虑空间电荷力。
2.2 束流聚焦的模拟研究
为了定量评估能量/流强差异较大的上升/下降沿对束流焦斑尺寸的影响,利用PIC代码ASTRA对逐束片的束流动力学行为进行了模拟仿真(含空间电荷力)。初始束片分布设为高斯分布,每个束片含50000个宏粒子,但在叠加获得聚焦后全束流分布时各束片粒子数按其电荷量加入权重因子。
根据模拟结果,焦斑位置处,中心束片的尺寸为
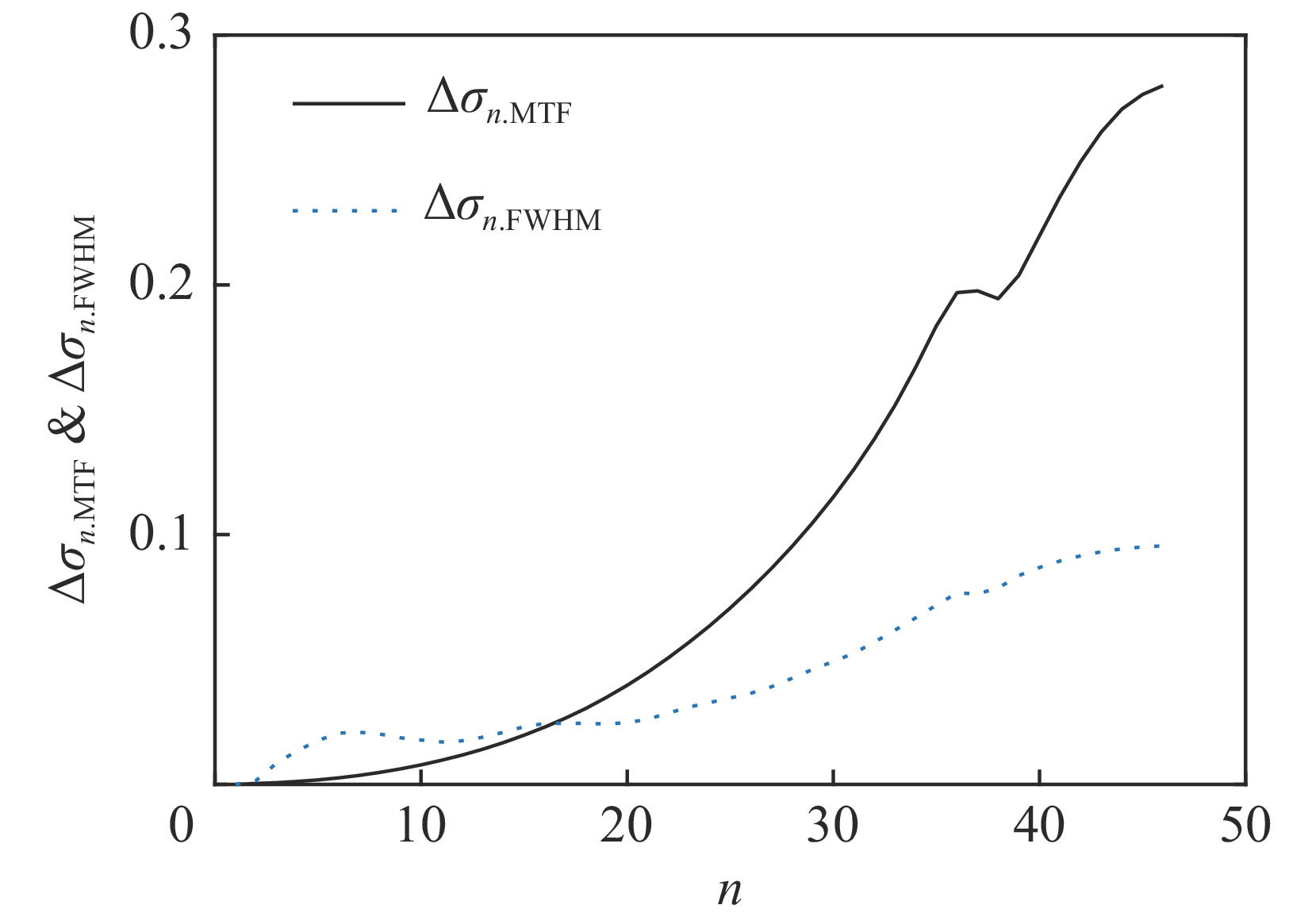
σ0.MTF=0.67mm ,σ0.FWHM=0.34mm ,发射度从200 µm增长至612 µm,尺寸的绝对值与理论分析值存在较大的差异,且σ0.MTF/σ0.FWHM= 1.98,中心束片底宽特征介于高斯分布和本涅特分布之间。可见约2 kA的流强下,空间电荷力会改变单束片聚焦后的分布特征,其非线性力已不可忽略。为了评估上升/下降沿束片叠加导致的束流尺寸增长,与图4、图5的解析结果进行比较,统计了中心束片与全束流聚焦后的分布(如图6所示),以及#(46−n)至#(46+n)号束片叠加分布的尺寸相对于中心束片尺寸的增长(如图7所示)。增长趋势与图5理论计算结果基本一致,全束流的MTF/FWHM尺寸与中心束片相比分别增长了约28.0%、9.8%,全束流的MTF尺寸与FWHM尺寸比值为
2.3 ,更接近于本涅特分布的底宽特征。2.3 计算结果分析
在理论估算(图4)中忽略了空间电荷力,并且假设焦点处束片呈高斯分布,是导致与模拟结果(图5)存在差异的主要原因。对比理论估算结果和模拟结果,虽然聚焦后束流尺寸绝对值差异较大,但是上升/下降沿叠加导致的束流相对尺寸增长趋势却比较一致,即理论模型可用于快速估算上升/下降沿能量差异导致的束流尺寸、底宽相对增长。
理论模型和模拟结果均表明,中心38 ns电子(n=17)的
Δσn.MTF 与Δσn.FWHM 增长量相等,对应的底宽特征与中心束片一致。中心38 ns区域束流强度基本一致,均方根能散为1.7%,则束流平顶区能散小于1.7%时,能散对底宽的影响可以忽略,这需要通过后续的注入器及腔压波形优化来实现。同时注意到从n=37至n=45之间,Δσn.FWHM 变化缓慢只增长约1.7%,而Δσn.MTF 增长8.5%,对束流底宽的增长贡献较大,该区间对应于上升/下降沿各10 ns的电子,流强小,对最终X射线照射量贡献较低,在后续研究中可考虑使用快速踢束器踢除、利用偏转段的能量—位置差异准直、或者利用不同能量束团的感应加速器振荡差异进行准直。3. 结 论
本文根据理论计算和数值模拟结果分析了一台直线感应加速器中上升/下降沿电子能量/流强差异对束流焦斑尺寸、底宽的影响。理论模型忽略了空间电荷力,与模拟结果存在一定差异,但能有效的反应上升/下降沿(能量差异较大)叠加导致的束流尺寸增长趋势,可以作为快速估算的手段。通过对模拟结果的分析,从提升注入器/腔压稳定性和踢除上升/下降沿角度,提出了减小束流底宽的具体指标,为下一步实验设计提供了理论指导。而聚焦前束片大小、位置、会聚角等不一致性对焦斑分布的影响与全束线磁场配置、准直误差等有关,需要从头至尾的PIC模拟来分析,将在后续工作中开展。
-
表 1 人工传输线阻抗变化对脉冲前沿的影响
Table 1. Simulated influence of PFN impedance on pulse front
C/pF Z/Ω tf/ns 1000 8 11.07 2000 5.7 15.06 4000 4 22.04 6000 3.3 26.08 表 2 PFN阻抗变化对脉冲前沿的影响
Table 2. Measured influence of PFN impedance PFN on pulse front
C/pF R/Ω tf/ns 400 10 13.8 2000 4.2 26.4 6000 2.8 40.8 -
[1] 李志强, 杨建华, 张建德, 等. 紧凑重频PFN-Marx发生器[J]. 强激光与粒子束, 2016, 28: 015013. doi: 10.11884/HPLPB201628.015013Li Zhiqiang, Yang Jianhua, Zhang Jiande, et al. A compact repetitive PFN-Marx generator. High Power Laser and Particle Beams, 2016, 28: 015013 doi: 10.11884/HPLPB201628.015013 [2] 高景明, 刘永贵, 刘金亮. 陡化前沿Marx发生器中开关过电压的研究[J]. 高电压技术, 2009, 35(1): 75-81. doi: 10.13336/j.1003-6520.hve.2009.01.031Gao Jingming, Liu Yonggui, Liu Jinliang. Investigation on over voltage of the spark gap switch in a wave erection Marx generator. High Voltage Engineering, 2009, 35(1): 75-81 doi: 10.13336/j.1003-6520.hve.2009.01.031 [3] 张江华, 杨汉武, 梁波, 等. MV级近方波Marx发生器的设计[J]. 强激光与粒子束, 2011, 23(11): 2877-2880. http://www.hplpb.com.cn/article/id/6765Zhang Jianghua, Yang Hanwu, Liang Bo. Design of MV level rectangle pulse Marx generator. High Power Laser and Particle Beams, 2011, 23(11): 2877-2880 http://www.hplpb.com.cn/article/id/6765 [4] 张晋琪, 吴朝阳, 杨周炳, 等. 1 MV小型重复频率Marx发生器的设计[J]. 强激光与粒子束, 2015, 27: 053003. doi: 10.11884/HPLPB201527.053003Zhang Jinqi, Wu Chaoyang, Yang Zhoubing. Design of 1 MV small repetitive Marx generator. High Power Laser and Particle Beams, 2015, 27: 053003 doi: 10.11884/HPLPB201527.053003 [5] Phelps D A. High density compact tunable PFN-Marx modulators[C]//IEEE Conference on Power Modulator Symposium. 1990: 507-510. [6] Kekez M M. A compact square waveform 15 kJ generator: 15 μs rising time, 7.5 Ω load impedance and 100-500 ns pulse width[C]//IEEE Pulsed Power Plasma Science Conference. 2001: 1027-1030. [7] Kekez M M. A 480 joule, 650 kV, < 3 ns risetime, 500 ns pulse width, compact pulse generator[C]//11th IEEE International Pulsed Power Conference. 1997: 1524-1529. [8] Hammon J, Lam S K, Drury D, et al. Compact l MV, 10 Hz pulser[C]//IEEE Pulse Power Conference. 1997: 147-152. [9] 张慧博. 基于脉冲变压器的长脉冲PFN-Marx发生器技术研究[D]. 长沙: 国防科技大学, 2013.Zhang Huibo. Study on long pulse PFN-Marx generator based on pulse transformers. Changsha: National University of Defense Technology, 2013 期刊类型引用(1)
1. 顾余辉. 直线加速器维修维护及质控措施研究分析. 中国设备工程. 2024(07): 48-50 .  百度学术
百度学术其他类型引用(0)
-





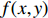

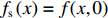
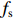
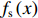
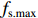
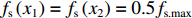
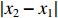
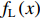
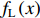
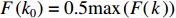
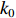
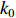

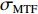
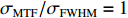
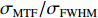
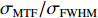
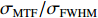

 下载:
下载:
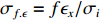
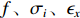
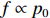
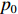
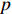
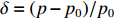
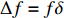
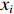
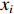
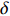
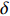
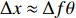
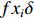
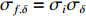
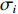
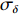

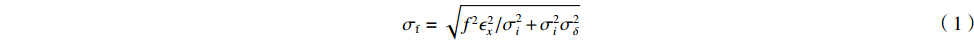
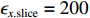

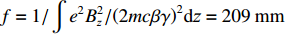
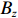
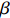
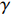


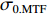

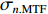

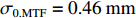
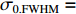
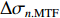
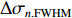
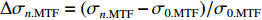
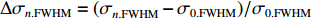
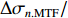
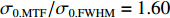

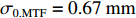
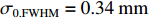
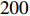
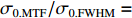


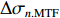
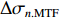
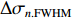
 下载:
下载: