Benchmarking verification of control rod effects on CMRR using MCNP codes throughout 3D core modeling and rod-drop experiment
-
摘要: 反应堆控制棒是核反应堆紧急控制和功率调节所不可缺少的控制部件,控制棒价值直接关系反应堆的停堆深度。采用MCNP和ORIGEN程序对CMRR反应堆全堆芯三维详细建模计算,并分别利用落棒法、逆动态法对控制棒积分价值、微分价值进行刻度,理论与实验吻合较好。单根安全棒的积分价值约大于4%Δk/k,事故工况下卡一根安全棒的停堆深度仍然大于10%Δk/k,验证了堆芯物理设计,保障了CMRR反应堆的运行安全。Abstract: In this research, MCNP code and ORIGEN code are used to calculate the control rod reactivity worth effects by simulating the 3D core model of CMRR reactor. The integral and differential behaviors of reactivity worth effects are measured by rod-drop experiments and digital inverse kinetic method with each other. The calculated and measured results are well accorded. The integral reactivity worth of one safety rod is about 4%Δk/k. Even in an accident when one safety rod gets stuck, the CMRR shutdown margin is still greater than 10%Δk/k, and CMRR is totally safe. So the physical design of CMRR is highly reliable and the operation could be safe.
-
Key words:
- control rod reactivity worth /
- MCNP code /
- CMRR /
- rod-drop experiments /
- inverse kinetic method
-
在X光闪光照相实验中[1-6],光源的尺寸及分布是影响成像质量的一个主要因素。光源点扩展函数的半高全宽(FWHM)作为一种描述焦斑尺寸的常用参数,多年来一直是表征光源性能的关键指标[7]。而近些年来,随着闪光照相技术的持续发展和对图像分辨率要求的不断提升,仅靠FWHM来描述光源的空间分辨率有其固有的局限,相关成像实验发现,如果光源点扩展函数不同,即使其FWHM相同,图像的分辨情况也会不同,因为束流分布的底宽也会对成像质量造成影响,为了充分考虑这一因素,美国LANL提出利用空间频域50%的调制传递函数(MTF)来评价光源尺寸[8-9],该参数也将成为下一步光源底宽优化的重要评价指标。
高剂量X光源通常来自高能电子束轰击高Z靶材产生的轫致辐射,光源分布很大程度上取决于击靶电子束的焦斑分布[10],优化电子束的焦斑分布是改善光源分布的重要手段。本文通过研究一台直线感应加速器中电子束的聚焦过程,着重分析束流上升/下降沿能量、流强不一致性等对束流焦斑FWHM与MTF尺寸的影响,为束流焦斑的进一步优化提供理论基础。考虑到直线感应加速器中电子束长度达到约30 m(持续时间约100 ns),全束流模拟需要大量计算资源,往往难以实现,本文将高能(约18 MeV)电子束流分割成约1.1 ns的束片,通过动态网格的PIC代码[11](含束流自身电磁力)模拟逐束片的聚焦过程,然后叠加形成最终束流分布。
1. 束斑尺寸描述方法简介型
这里以常用的光斑尺寸描述方法来描述电子束打靶焦斑,设电子束的横向分布函数为
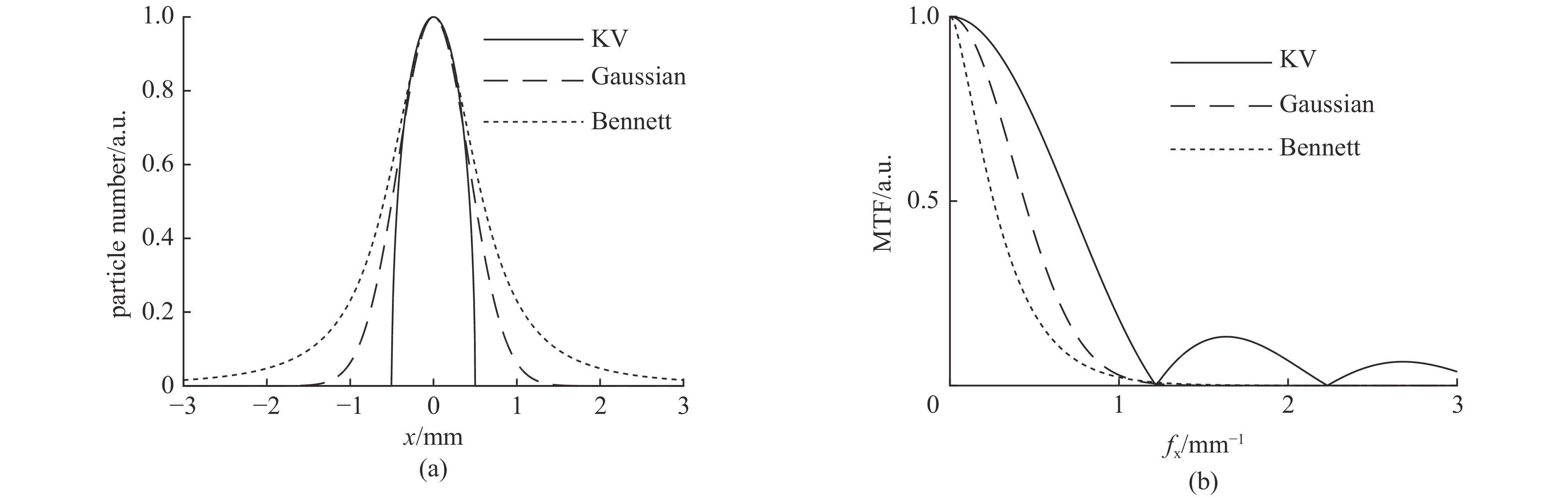
f(x,y) ,则其对应的线扩展函数fL(x)=∫f(x,y)dy ,点扩展函数为fs(x)=f(x,0) 。FWHM尺寸指其点扩展函数fs 的半高全宽,记fs(x) 的最大值为fs.max ,且有fs(x1)=fs(x2)=0.5fs.max ,则束流的FWHM尺寸为|x2−x1| ,该参数主要反映有效应用区域的尺寸,是实验中常用的评价指标。调制传递函数(MTF)等效均匀分布尺寸描述线扩展函数fL(x) 的空间频域特性,设线扩展函数fL(x) 的傅里叶变换为F(k),且有F(k0)=0.5max(F(k)) ,则束流的MTF尺寸为0.705/k0 (0.705为均匀圆盘分布情况下k0 与半高全宽的乘积),该参数对于分布的底宽较为敏感。直线感应加速器中常用的束流分布表征函数有均匀分布(KV)、高斯分布(Gaussian)和本涅特(Bennett)分布,在相同的FWHM时,三种分布的底宽和MTF焦斑依次增大,其分布曲线(线扩展函数)及对应的空间频域曲线如图1所示。在三种分布函数下,FWHM尺寸
σFWHM 和MTF尺寸σMTF 有线性对应关系,如表1所示。均匀布时σMTF/σFWHM=1 ,高斯分布和本涅特分布的底宽依次增大,σMTF/σFWHM 分别为1.6和2.7,可见σMTF/σFWHM 值与分布底宽呈正相关,后文的分析中将通过σMTF/σFWHM 来判断束流的分布及其底宽特征。表 1 不同分布函数下,FWHM尺寸与MTF尺寸的对应关系Table 1. Relationship between the FWHM beam size and the MTF beam size in various distributionsf(x) σFWHM/mm k0/mm−1 σMTF/mm KV 1.00 0.705 1.00 Gaussian 1.00 0.441 1.60 Bennett 1.00 0.258 2.70 2. 能散对束流聚焦影响
2.1 束流聚焦的理论分析
忽略空间电荷效应以及透镜像差,单能电子束在聚焦平面处的均方根尺寸主要受限于束流发射度,近似表示为
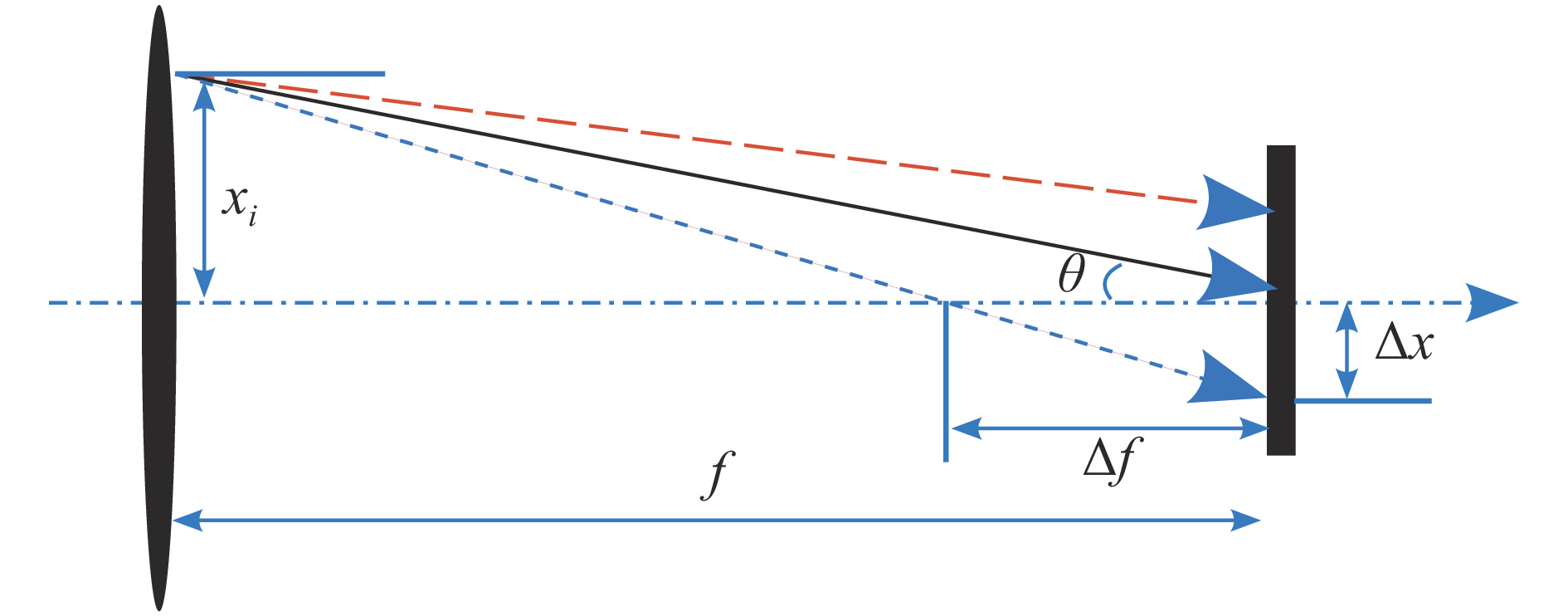
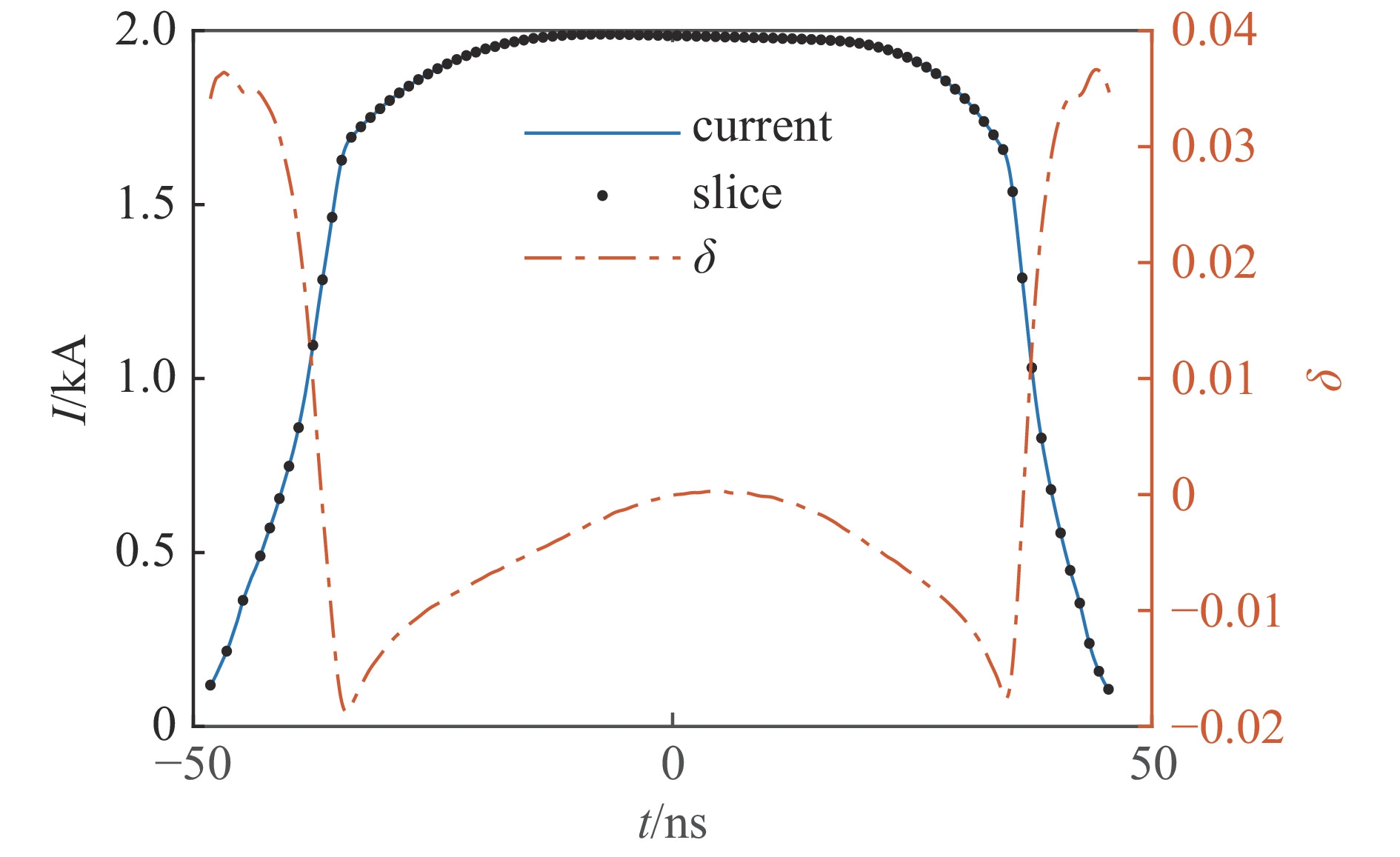
σf.ϵ=fϵx/σi ,其中f、σi、ϵx 分别为焦距,束流初始均方根半径及发射度[12]。焦距与电子束的能量正相关即f∝p0 (p0 为参考电子的能量),一个能量为p 的电子与参考电子的相对能量差异为δ=(p−p0)/p0 ,经过聚焦线圈后焦距差异为Δf=fδ ,如图2所示。一般而言,电磁透镜的焦距远大于焦斑尺寸,则根据图2易得初始位置为xi 、相对能量差异为δ 的电子在焦点处的横向位置为Δx≈Δfθ =fxiδ ,则受能散限制的焦斑尺寸可近似表示为σf.δ=σiσδ ,其中σi 和σδ 分别为束流的均方根半径和均方根能散,即xi 和δ 的均方根值。由于能散与发射度的影响相互独立,最终焦斑尺寸可以表示为σf=√f2ϵ2x/σ2i+σ2iσ2δ (1) 公式(1)的推导中忽略了束流聚焦前后发射度变化,这在横向非线性力较弱时对于薄束片而言是适用的。以一组实验参数作为计算输入条件:束流的能散分布由加速腔腔压叠加并考虑束流负载效应后获得,中心束片能量17 MeV,如图3虚线所示,流强波形通过B-dot测量获得如图3实线所示,切片发射度
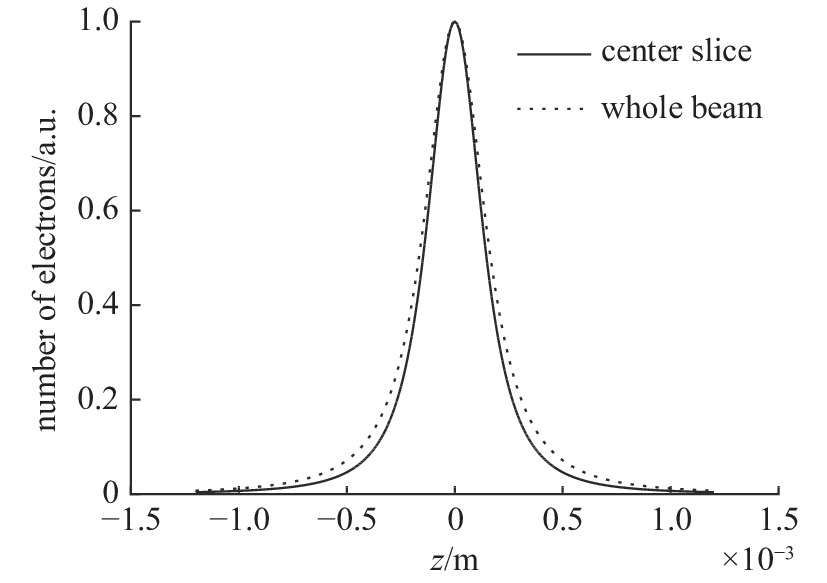
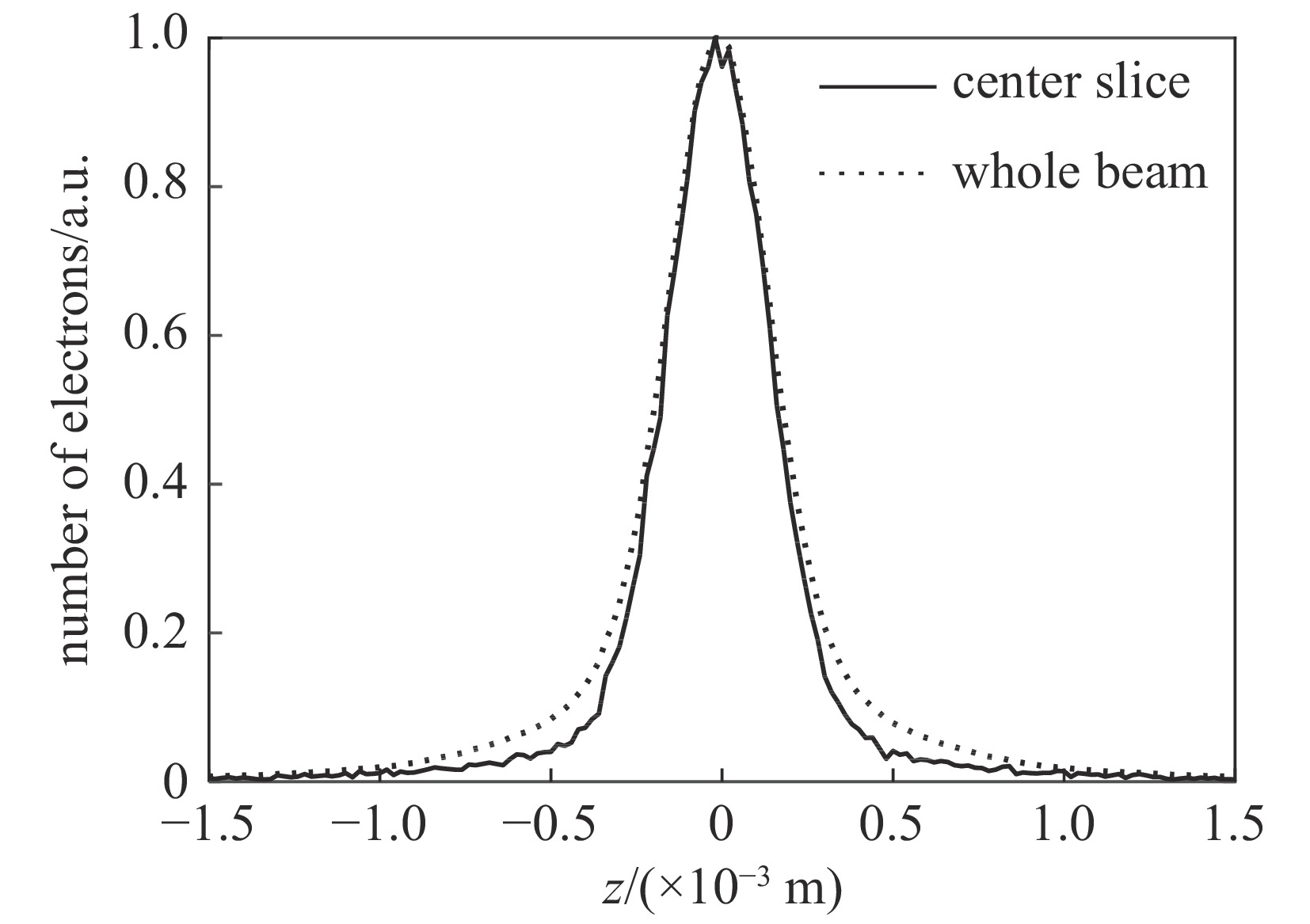
ϵx.slice=200 µm,束流聚焦前尺寸σi=10mm ,根据螺线管磁场求得中心束片的焦距f=1/∫e2B2z/(2mcβγ)2dz=209mm ,其中m,e分别为电子的质量和电荷量,Bz 为聚焦磁场强度,β 为电子经光速归一化的速度,γ 为洛伦兹系数,z为轴向坐标变量。将图3所示束流分为91个1.1 ns的切片(从左到右依次编号,中心束片为#46),将其能量差分别代入公式(1)可估算逐束片聚焦后的均方根尺寸。假设聚焦后单束片呈高斯分布,将束片分布按权重叠加即可得到聚焦后整个束流的横向分布,束片权重为其归一化电荷量。根据公式(1)计算得到的中心束片(#46)及整个束流(#1-#91束片叠加)的焦斑分布如图4所示,中心束片以实线表示,整个束流以虚线表示,可见整个束流的底宽明显大于中心束片,但是半高宽差异并不明显。
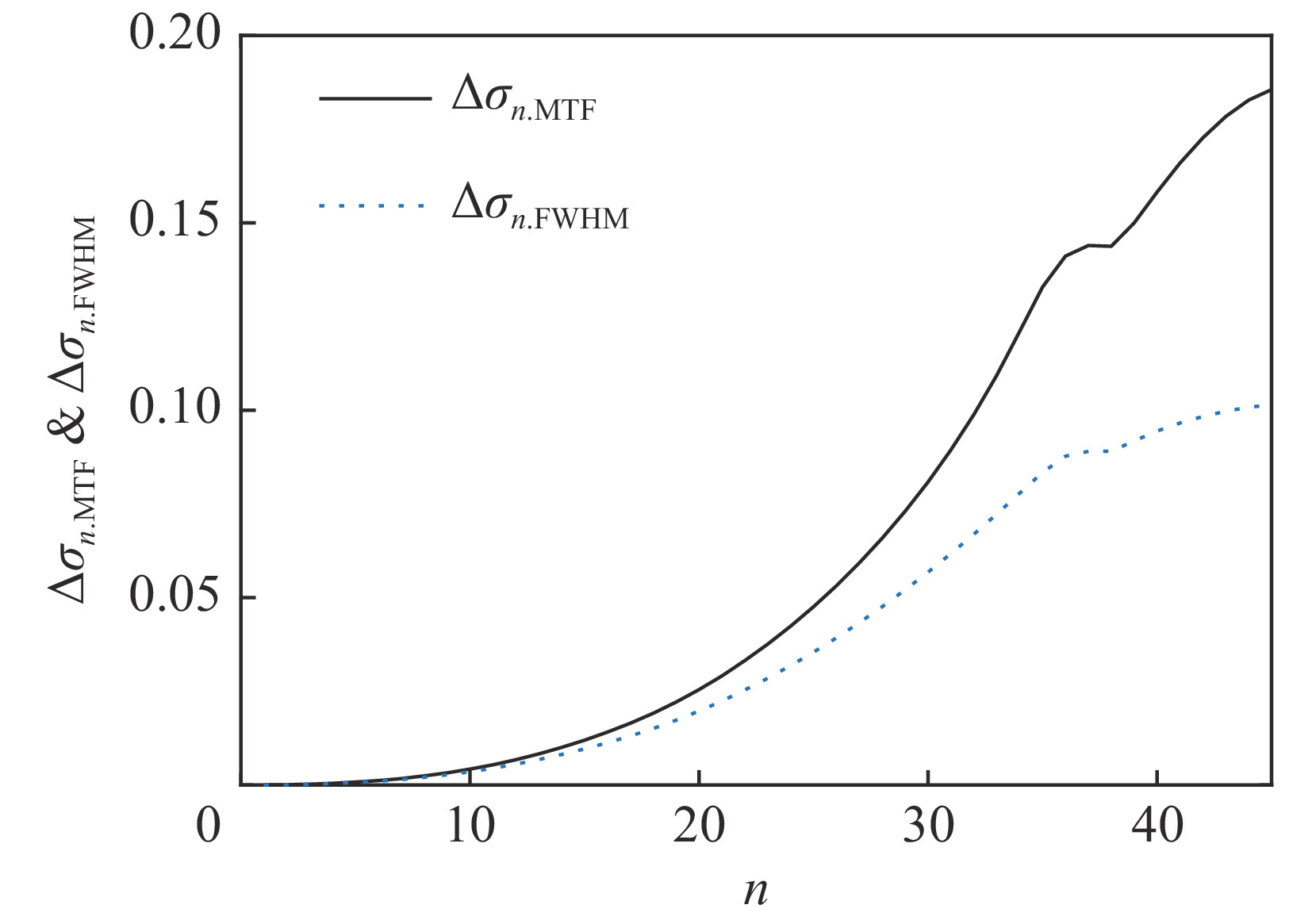
将中心束片聚焦后的MTF和FWHM尺寸分别记为
σ0.MTF 和σ0.FWHM ,将#(46-n)号束片至#(46+n)号束片聚焦后叠加分布的MTF和FWHM尺寸分别记为σn.MTF 和σn.FWHM 。根据计算结果可得在焦点位置处σ0.MTF=0.46mm ,σ0.FWHM=0.29mm ,为了分析上升/下降沿叠加后对束流尺寸、分布的影响,进一步计算了n分别取值1~45时叠加分布的MTF/FWHM尺寸相对于中心束片的增长量,将相对增长量表示为Δσn.MTF 和Δσn.FWHM ,其中Δσn.MTF=(σn.MTF−σ0.MTF)/σ0.MTF ,Δσn.FWHM=(σn.FWHM−σ0.FWHM)/σ0.FWHM ,计算结果如图5所示。可见上升/下降沿束片的叠加使得束流绝对尺寸逐渐增大,但MTF尺寸的增长幅度明显高于FWHM尺寸,即Δσn.MTF/Δσn.FWHM 比值随n增大,束流底宽随n的增大逐渐增长。全束流的MTF/FWHM尺寸与中心束片相比分别增长了约18.6%/10.1%,单束片呈高斯分布有σ0.MTF/σ0.FWHM=1.60 ,而全束片叠加后的MTF尺寸与FWHM尺寸比值增长至1.73,对比表1数据可知,全束流分布介于高斯分布和本涅特分布之间。上述估算中束片间的唯一差异为能量,可见减小束流能散可以有效的控制束流底宽,减小束流的MTF尺寸。但是由于中间束片的电荷量较大,而上升/下降沿束片电荷量小,束片内的空间电荷力并不一致,因此对束片内分布的影响也不一致,定量评估能散/流强对束流聚焦后尺寸影响需要考虑空间电荷力。
2.2 束流聚焦的模拟研究
为了定量评估能量/流强差异较大的上升/下降沿对束流焦斑尺寸的影响,利用PIC代码ASTRA对逐束片的束流动力学行为进行了模拟仿真(含空间电荷力)。初始束片分布设为高斯分布,每个束片含50000个宏粒子,但在叠加获得聚焦后全束流分布时各束片粒子数按其电荷量加入权重因子。
根据模拟结果,焦斑位置处,中心束片的尺寸为
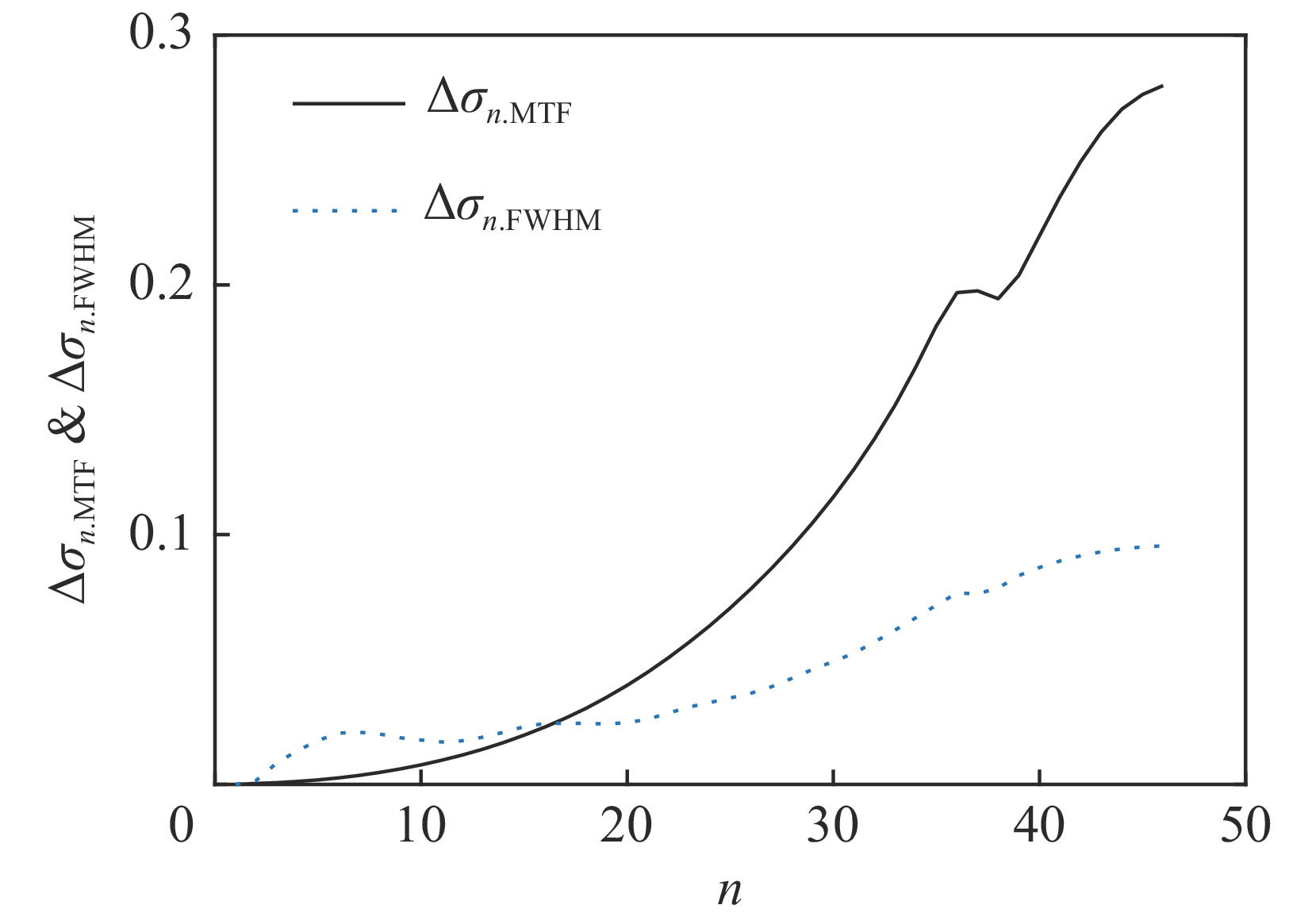
σ0.MTF=0.67mm ,σ0.FWHM=0.34mm ,发射度从200 µm增长至612 µm,尺寸的绝对值与理论分析值存在较大的差异,且σ0.MTF/σ0.FWHM= 1.98,中心束片底宽特征介于高斯分布和本涅特分布之间。可见约2 kA的流强下,空间电荷力会改变单束片聚焦后的分布特征,其非线性力已不可忽略。为了评估上升/下降沿束片叠加导致的束流尺寸增长,与图4、图5的解析结果进行比较,统计了中心束片与全束流聚焦后的分布(如图6所示),以及#(46−n)至#(46+n)号束片叠加分布的尺寸相对于中心束片尺寸的增长(如图7所示)。增长趋势与图5理论计算结果基本一致,全束流的MTF/FWHM尺寸与中心束片相比分别增长了约28.0%、9.8%,全束流的MTF尺寸与FWHM尺寸比值为
2.3 ,更接近于本涅特分布的底宽特征。2.3 计算结果分析
在理论估算(图4)中忽略了空间电荷力,并且假设焦点处束片呈高斯分布,是导致与模拟结果(图5)存在差异的主要原因。对比理论估算结果和模拟结果,虽然聚焦后束流尺寸绝对值差异较大,但是上升/下降沿叠加导致的束流相对尺寸增长趋势却比较一致,即理论模型可用于快速估算上升/下降沿能量差异导致的束流尺寸、底宽相对增长。
理论模型和模拟结果均表明,中心38 ns电子(n=17)的
Δσn.MTF 与Δσn.FWHM 增长量相等,对应的底宽特征与中心束片一致。中心38 ns区域束流强度基本一致,均方根能散为1.7%,则束流平顶区能散小于1.7%时,能散对底宽的影响可以忽略,这需要通过后续的注入器及腔压波形优化来实现。同时注意到从n=37至n=45之间,Δσn.FWHM 变化缓慢只增长约1.7%,而Δσn.MTF 增长8.5%,对束流底宽的增长贡献较大,该区间对应于上升/下降沿各10 ns的电子,流强小,对最终X射线照射量贡献较低,在后续研究中可考虑使用快速踢束器踢除、利用偏转段的能量—位置差异准直、或者利用不同能量束团的感应加速器振荡差异进行准直。3. 结 论
本文根据理论计算和数值模拟结果分析了一台直线感应加速器中上升/下降沿电子能量/流强差异对束流焦斑尺寸、底宽的影响。理论模型忽略了空间电荷力,与模拟结果存在一定差异,但能有效的反应上升/下降沿(能量差异较大)叠加导致的束流尺寸增长趋势,可以作为快速估算的手段。通过对模拟结果的分析,从提升注入器/腔压稳定性和踢除上升/下降沿角度,提出了减小束流底宽的具体指标,为下一步实验设计提供了理论指导。而聚焦前束片大小、位置、会聚角等不一致性对焦斑分布的影响与全束线磁场配置、准直误差等有关,需要从头至尾的PIC模拟来分析,将在后续工作中开展。
-
表 1 核燃料原子密度对反应堆有效增值因子(keff)的影响
Table 1. Effect on effective multiplication factor(keff) of nuclear fuel atomic density
percentage of nuclear fuel nominal value/% atomic density of nuclear fuel /1024 first criticality keff standard error 100 0.054 08 0.054 08 1.003 21 0.000 04 102 0.055 16 - 1.006 25 0.000 04 98 0.053 00 - 1.000 16 0.000 04 表 2 主要物理参数(轻水温度)对反应堆有效增值因子(keff)的影响
Table 2. Effect on effective multiplication factor(keff) of light water temperature
temperature of light water/℃ atomic density of light water/1024 first criticality keff standard error 13 0.100 32 0.100 32 1.003 21 0.000 04 20 0.100 20 - 1.002 97 0.000 04 30 0.099 95 - 1.001 99 0.000 04 40 0.099 60 - 1.000 79 0.000 04 表 3 主要物理参数(重水温度)对反应堆有效增值因子(keff)的影响
Table 3. Effect on effective multiplication factor(keff) of heavy water temperature
temperature of heavy water/℃ atomic density of heavy water/1024 first criticality keff standard error 13 0.100 00 0.100 00 1.003 21 0.000 04 20 0.099 86 - 1.003 26 0.000 04 30 0.099 56 - 1.003 20 0.000 04 表 4 CMRR的带燃耗临界棒位计算结果
Table 4. Critical rod position considering burnup of the fuel element
rod position in the zero power condition/mm keff calculated with codes MCNP and ORIGEN standard error beginning of first core loading 311 1.003 21 0.000 04 end of first core loading 433 1.002 78 0.000 04 beginning of second core loading 350 1.006 03 0.000 04 end of second core loading 448 0.999 46 0.000 04 beginning of third core loading 328 0.998 22 0.000 04 表 5 首次临界控制棒反应性价值
Table 5. Reactivity worth of control rod in the first critical core
theoretical value/(Δk/k) experimental value/(Δk/k) method 1# safety rod reactivity worth -0.045 13 — rod drop 2# safety rod reactivity worth -0.046 07 — rod drop 1# safety rod reactivity worth -0.040 17 -0.039 90 compensation 2# safety rod reactivity worth -0.038 73 -0.038 30 compensation 1# regulating control rod reactivity worth -0.031 95 -0.030 81 alternate motion 2# regulating control rod reactivity worth -0.032 44 -0.031 47 alternate motion 表 6 第二次换载后落棒法测量控制棒反应性价值实验结果与理论结果
Table 6. Rod value results throughout modeling and rod-drop experiment after the second core loading
theoretical value/(Δk/k) experimental value/(Δk/k) 1# safety rod reactivity worth with 0.054 59 0.050 81 2# safety rod reactivity worth with 0.053 55 0.053 06 1#+2# safety rod reactivity worth with 0.139 46 0.132 70 shutdown margin with 2# safety rod stuck 0.151 29 0.108 40 shutdown margin 0.301 67 0.242 60 -
[1] IAEA. Utilization-related design features of research reactors: a compendium[R]. Technical Report No. 455, 2007. [2] IAEA. Safety analyses for research reactors[R]. Safety Report No. 55, 2008. [3] IAEA. Core management and fuel handling for research reactors[R]. Safety Standard No. NS-G-4.3, 2008. [4] IAEA. Operational limits and conditions and operating procedures for research reactors[R]. Safety Standard No. NS-G-4.4, 2008. [5] ORNL. WIMS-D4: Winfrith Improved Multigroup Scheme code system[R]. Code CCC-575, 1991. [6] Fowler T B, Vondy D R, Cunningham G W, et al. Nuclear reactor core analysis code: CITATION[R]. ORNL-TM-2496, 1971. [7] ORNL. Scale: A comprehensive modeling and simulation suite for nuclear safety analysis and design[R]. ORNL-TM-39, 2005. [8] Briesmeister J F. MCNP—A general Monte Carlo N-particle transport code version 4C[R]. LA-13709-M, 2000. [9] 黄洪文, 叶林, 钱达志, 等. 新型铪控制棒的研制[J]. 核动力工程, 2008, 29(3): 48-51. https://www.cnki.com.cn/Article/CJFDTOTAL-HDLG200803012.htmHuang Hongwen, Ye Lin, Qian Dazhi, et al. Development and manufacture of new-style hafnium control rod. Nuclear Power Engineering, 2008, 29(3): 48-51 https://www.cnki.com.cn/Article/CJFDTOTAL-HDLG200803012.htm [10] MacFarlane R E. Data testing for ENDF/B-Ⅶ[R]. Los Alamos National Laboratory, 2011. [11] 李润东, 代君龙, 王学杰. 300#堆周期和反应性数字化测量技术研究[C]//第五届全国核仪器及其应用学术会议. 2007: 188-191.Li Rundong, Dai Junlong, Wang Xuejie. Measurement digitalization for period and reactivity of SPRR-300//Proceedings of the China Conference on Nuclear Instrument Application & Nuclear Detection Technology & Nuclear Measurement Method. 2007: 188-191 期刊类型引用(1)
1. 顾余辉. 直线加速器维修维护及质控措施研究分析. 中国设备工程. 2024(07): 48-50 .  百度学术
百度学术其他类型引用(0)
-





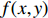

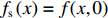
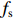
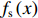
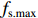
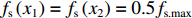
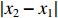
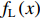
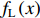
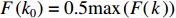
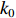
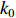

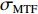
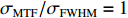
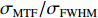
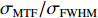
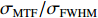

 下载:
下载:
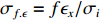
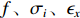
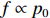
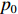
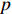
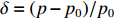
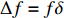
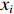
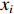
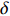
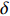
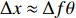
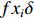
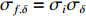
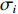
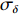

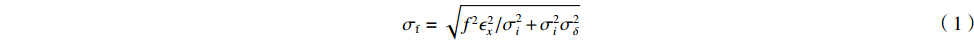
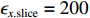

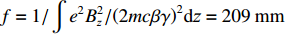
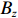
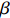
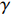


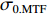

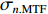

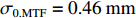
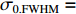
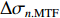
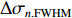
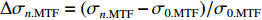
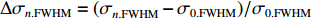
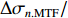
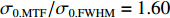

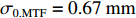
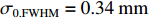
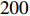
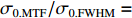
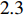


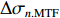
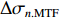
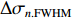
 下载:
下载: