Design and experimental study of compact pulse power driver
-
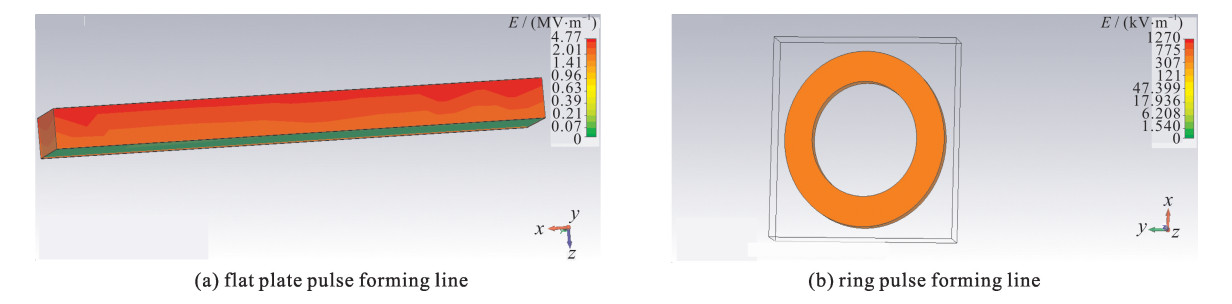
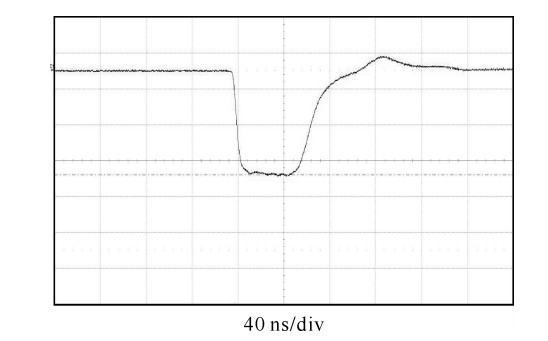
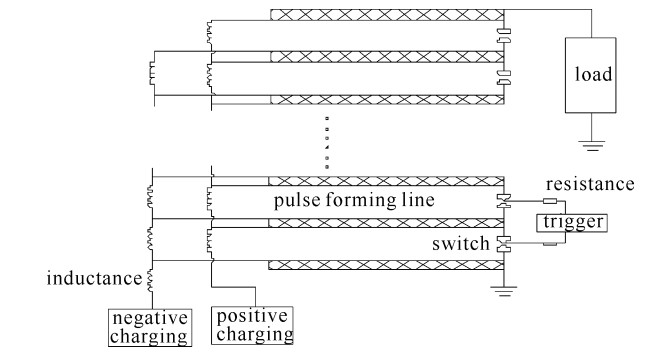
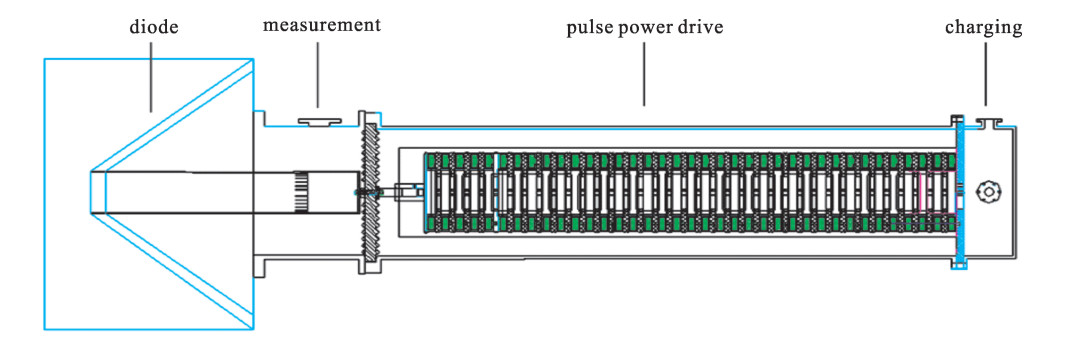
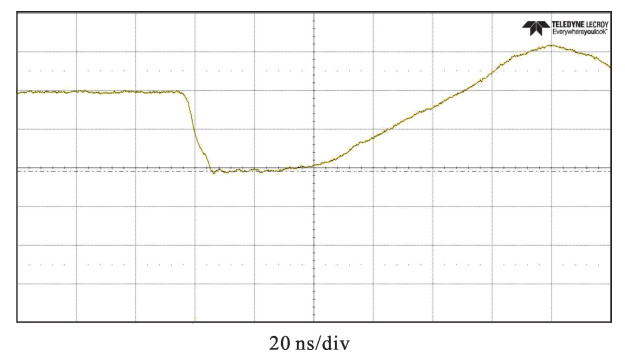
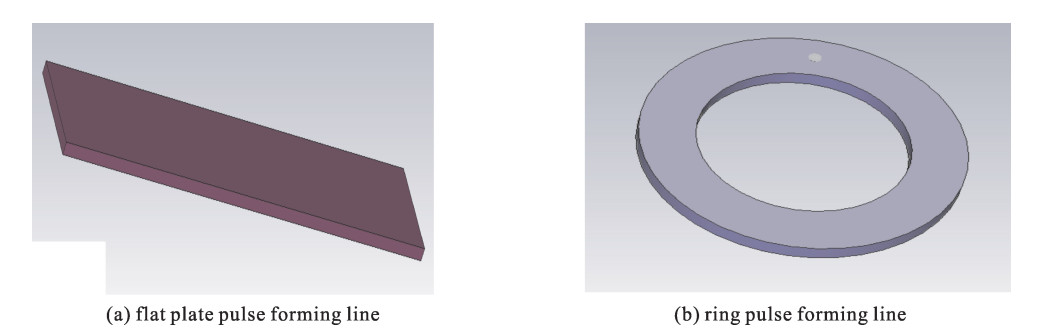
摘要: 利用碳酸钡基材料研制了一种环形脉冲形成线。对脉冲形成线的材料特性、电场分布对耐压影响进行分析和研究，通过优化结构设计、材料特性，提高了环形脉冲形成线的耐压水平。利用此脉冲形成线建立了37级Marx发生器，此发生器通过电感进行并联充电和串联放电工作。使用电磁仿真软件对系统结构进行了三维电场分析，分析结果表明, 采用此环形脉冲形成线能够实现同轴设计，电场更加均匀，确定了满足紧凑化的最佳外形尺寸。实验结果表明, 设计的脉冲功率驱动源在充电电压为±19 kV的条件下，在二极管负载下得到了输出半高宽为65 ns、电压为680 kV的快高压脉冲。Abstract: The ring pulse forming line which uses BaTiO3 material is developed. Material characteristics and the influence of electric field distribution on the electric strength of the pulse forming line are analyzed. Due to optimizations of structure design and material characteristics, the electric strength of the pulse forming line has been enhanced. A 37-stage compact Marx generator is designed based on the pulse forming line. The electric field intensity distributions of the configuration with inductances were simulated. According to the results of the simulation, the electric field of the configuration is uniform and gives an optimized contour dimension. In the experiment, when the PFL was charged at ±19 kV, the output voltage was more than 680 kV and the pulse width was about 65 ns on the matching load.
-
Key words:
- pulse power technology /
- Marx generator /
- pulse forming line /
- miniaturization
-
目前，中国原子能科学研究院正在研制我国具有自主知识产权的一台230 MeV医用超导回旋加速器[1-2]，用于癌症治疗。在超导回旋加速器中，为了保持加速过程中粒子轨迹半径的稳定增长，优化束流的径向进动，减小加速区域的相干振荡振幅，提高引出区的束流引出效率，要求束流在中心区具有良好对中、在引出区局部增大径向圈间距。在设计中通常采用在磁极表面安装调谐线圈的方式[3-4]或者采用磁场调节棒的方式[5-7]来提供束流对中所需的磁场。与调谐线圈相比，磁场调节棒具有结构简单、无源、没有热负载和可靠性高等优点，因此230 MeV超导回旋加速器采用磁场调节棒的方式[8]。磁场调节棒在加速器主磁铁中精确运动对于加速器调试运行起到极其重要的作用。本文根据磁场调节棒的物理设计需求，设计了磁场调节棒总体控制方案，研制了16套磁场调节棒驱动及其控制系统，对每套系统进行位置标定，并在实际运行工况下进行测试，实现了物理设计提出的各项指标。此外，根据医用电气设备电磁兼容要求，对该系统进行内部测试，测试结果满足YY 0505-2012/IEC 6060 1-1-2:2004标准要求。
1. 束流对中调节器
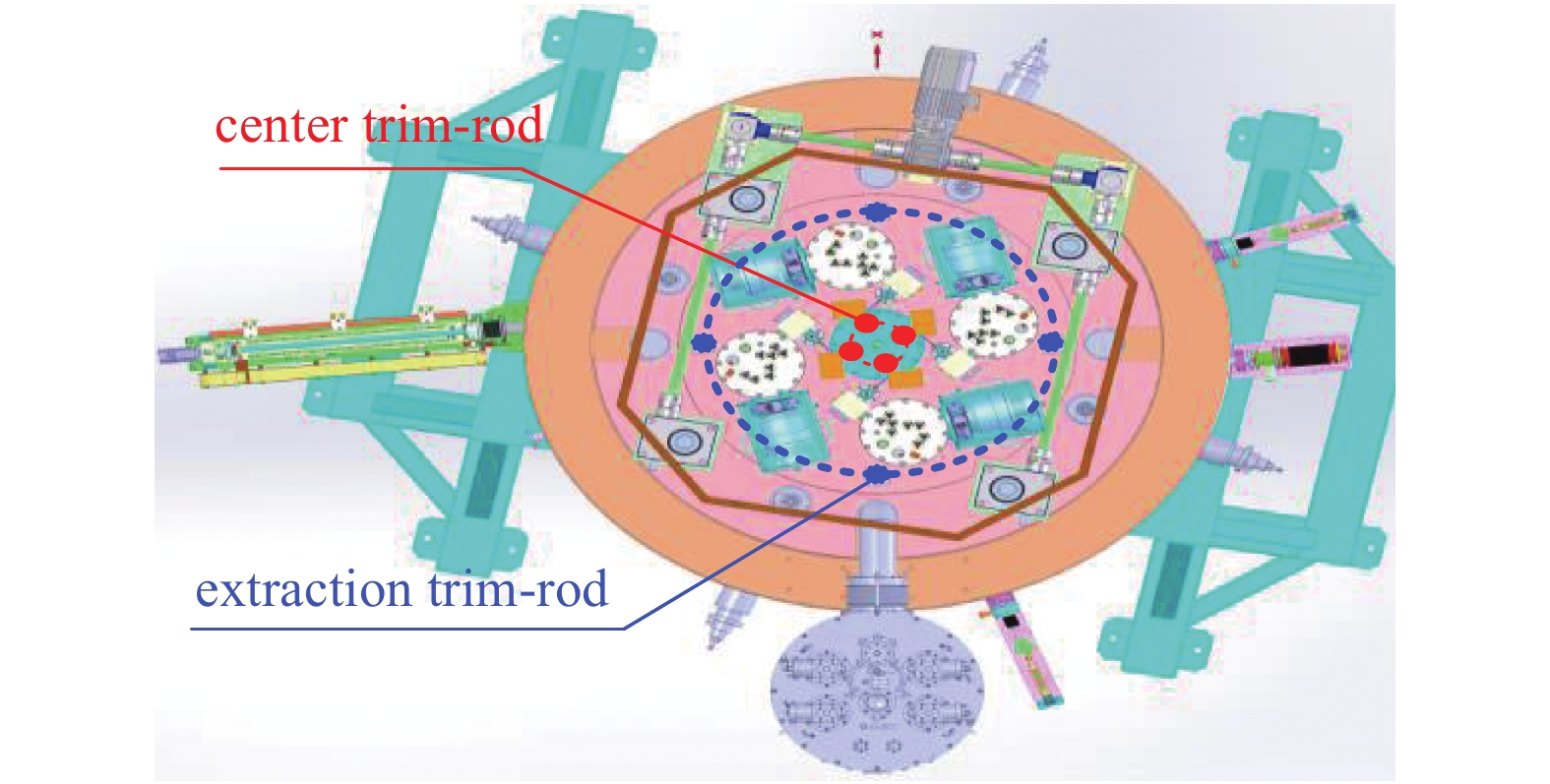
230 MeV超导回旋加速器采用两组磁场调节棒（共16个）作为束流对中调节器，分别置于中心区（8个，上下磁极各4根）和引出区（8个，上下磁极各4根），如图1所示。所有磁场调节棒的直径为30 mm，中心区磁场调节棒位于半径130 mm处，长度805 mm，引出区磁场调节棒位于半径790 mm处，长度768 mm。中心区磁场调节棒具有两个方面的用途：一是通过独立调整每个调节棒的位置产生磁场一次谐波，调节粒子的对中；二是通过同步调整所有调节棒的位置，改善中心区磁场的等时性。引出区磁场调节棒主要用于产生共振进动引出所需的特定幅值、相位的一次谐波，提高引出效率[8]。
1.1 磁场调节基本原理
磁场调节棒产生一次谐波的过程中需要保证磁场关于中心平面对称，所以上下磁轭中的磁场调节棒应同步移动，保持关于中心平面对称。因此，在移动磁场8根磁场调节棒的过程中应将其分为4对，设4对磁场调节棒的高度分别为
${{\textit{z}}_1}$ 、${{\textit{z}}_2}$ 、${{\textit{z}}_3}$ 、${{\textit{z}}_4}$ ，基线高度是${{\textit{z}}_0}$ 。对于安装在
$\theta $ 方位角、高度为${\textit{z}}$ 的磁场调节棒，它产生的谐波场${B_{\textit{z}}}\left( {\theta ,{\textit{z}}} \right)$ 可以表示为Bz(θ,z)=Bz0(z)+Bz1(z)cos(θ−θ0)+Bz2(z)cos2(θ−θ0)+⋯ (1) 不同高度下谐波幅值的比例
${C_{\rm{i}}}$ 基本不变，令Ci=Bzi(0)Bz0(0)≈Bzi(z)Bz0(z) (2) 式（1）可简化为
Bz(θ,z)=Bz0(z)(1+C1cos(θ−θ0)+C2cos2(θ−θ0)+⋯) (3) 在磁场调节棒移动范围很小时，认为平均场随高度的变化是线性的，设线性系数分别为
$a$ 、$b$ ，则Bz0(z)=az+b (4) 考虑依次安装在方位角
${\theta _0}$ 、${\theta _0} + {90^ \circ }$ 、${\theta _0} + {180^ \circ }$ 、${\theta _0} + {270^ \circ }$ 的4对磁场调节棒，产生的平均场${B_0}$ 、一次谐波${B_1}\left( \theta \right)$ 、二次谐波${B_2}\left( \theta \right)$ 的总和分别为B0=a(z1+z2+z3+z4)+4b (5) B1(θ)=C1a√(z1−z3)2+(z2−z4)2cos[θ−θ0+tan−1(z2−z4z1−z3)] (6) B2(θ)=C2a(z1−z2+z3−z4)cos(2θ−2θ0) (7) 磁场调节棒产生一次谐波的过程中，不应改变平均场和产生二次谐波，所以
{a(z1+z2+z3+z4)+4b=4(az0+b)C2a(z1−z2+z3−z4)cos(2θ−2θ0)=0 (8) 解得
{z1+z3=2z0z2+z4=2z0 (9) 设
$\Delta {{\textit{z}}_1} = {{\textit{z}}_1} - {{\textit{z}}_0} = {{\textit{z}}_0} - {{\textit{z}}_3}$ 、$\Delta {{\textit{z}}_2} = {{\textit{z}}_2} - {{\textit{z}}_0} = {{\textit{z}}_0} - {{\textit{z}}_4}$ ，可由式（6）得一次谐波幅值${B_1}$ 和相位${\theta _1}$ 分别为B1=C1a√Δz12+Δz22 (10) θ1=θ0−tan−1Δz2Δz1 (11) 1.2 磁场调节棒主要参数设计
使用有限元软件计算中心区不同磁场调节棒高度下的磁场，0.1 mm步长对一次谐波幅值的调节量约0.5 Gs，±10 mm行程可产生45 Gs的一次谐波。基于有限元模型的算法可计算移动调节棒带来的理论磁场变化[8]，从而确定磁场调节棒运动控制定位精度0.1 mm。在测量场上叠加一次谐波场得到新的磁场，作为粒子跟踪程序使用的磁场。模拟结果表明，为了调节230 MeV超导回旋加速器束流对中，需要磁场调节棒产生幅值20 Gs、相位90°的一次谐波。在直边扇形模型中将圆柱体的调节棒等效为截面积相等方形柱体，计算中心区和引出区磁场调节棒的受力如下，中心区和引出区磁场调节棒最大受力为1400 N，磁场调节棒的自重为47 N，相比磁场力可忽略，可设定1.5倍的余量，取最大驱动力指标为2100 N。230 MeV超导回旋加速器磁场调节棒驱动系统技术参数，如表1所示。
表 1 CYCIAE-230磁场调节棒驱动系统技术参数Table 1. Parameters of Trim-rod drive system on CYCIAE-230parameter technical indicator maximum driving force/N 2100 center stroke/mm ±10 extraction stroke/mm ±30 positioning accuracy/mm 0.1 repeat positioning accuracy/mm 0.05 magnetic shielding effect/Gs ＜200 power self-locking needed limit switch needed 230 MeV超导回旋加速器磁场调节棒驱动系统主要难点如下：磁场调节棒数量多，运动精度高；工作在较强的电离辐射场中位置传感器无法使用光栅尺或磁栅尺等高分辨率的数字传感器，只能采用模拟电子尺[9-10]；上下磁轭中的两根磁场调节棒相向运动，最终位置保持相对中心平面的对称性；运动驱动机构工作区域的漏磁场非常强；驱动机构安装空间非常狭小，仅ϕ90 mm；加速器中心磁场达到2.35 T，调节棒在磁场中移动时会受到非常强的阻碍相对运动的磁场力作用。
1.3 磁场调节棒工作方式
在主磁铁测磁阶段，将中心区和引出区磁场调节棒置于基线位置，并进行垫补。多次改变磁场调节棒位置进行主磁铁磁场测量，验证磁场调节棒磁场的物理计算。
在加速器调试阶段，相差180º的上下两根磁场调节棒，向相反方向移动。在调试时，验证从径向靶测量结果到一次谐波幅值与相位的算法以及从相位到四组磁场调节棒位置的算法，并研究磁场调节棒调节量与温度、主磁铁励磁电流的关系。
在加速器运行阶段，磁场调节棒位置只需要微调，控制系统分析温度、主磁铁励磁电流、束流诊断信号，给出最终的磁场调节棒位置值。
2. 磁场调节棒驱动装置设计
2.1 驱动系统总体方案
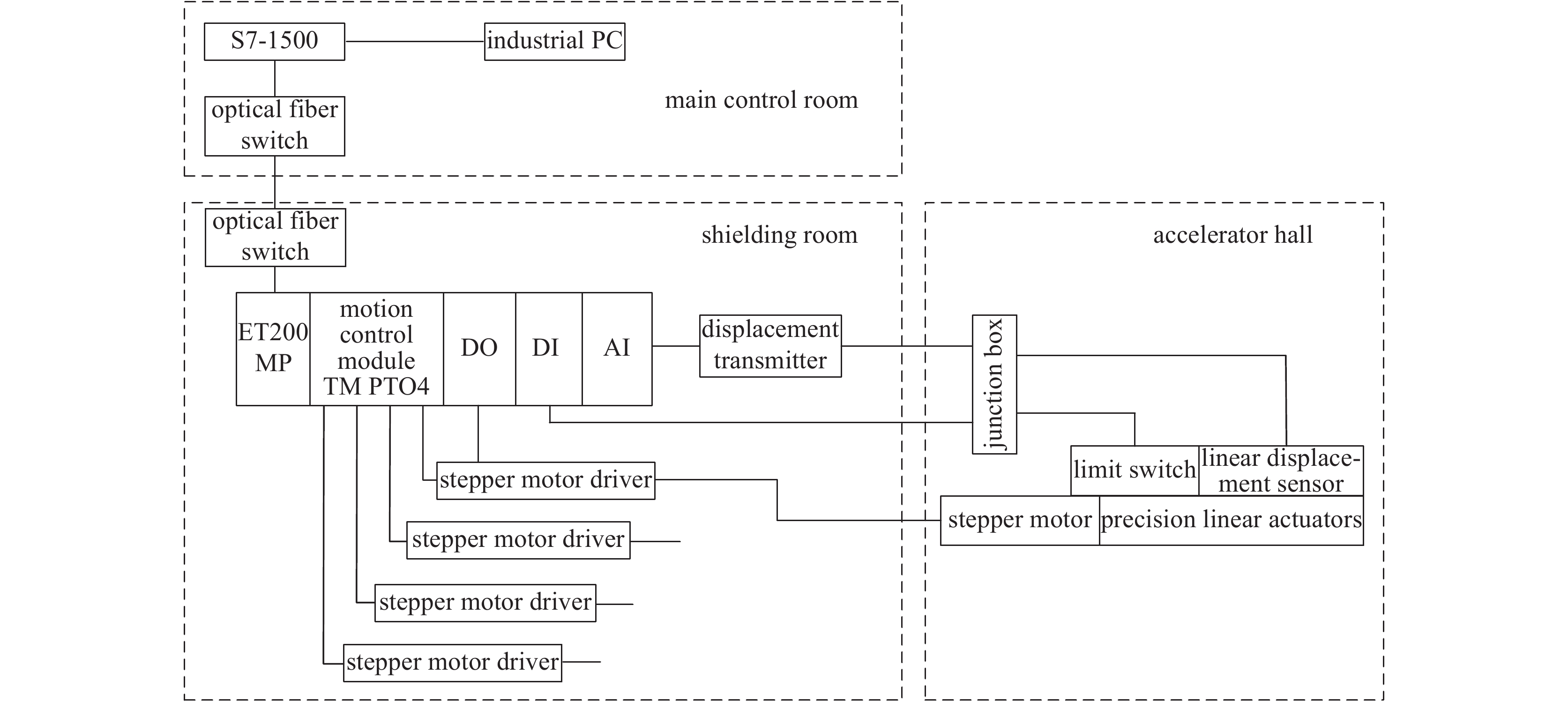
磁场调节棒驱动控制系统由上位工控机、可编程控制器（PLC）、光纤通讯模块、驱动器、步进电机、直线执行器和直线位移传感器等模块组成，驱动控制系统示意图，如图2所示。步进电机、直线执行器、直线位移传感器、限位开关等位于加速器大厅内的超导回旋加速器上；PLC子站、PLC分布式I/O系统、工艺模块、驱动器和位移变送器均安装在控制机柜内，置于加速器大厅屏蔽间内；工控机、PLC的主控制器等位于主控制内部的控制机柜。主控制室内PLC主控制器通过自身集成的Profinet现场总线接口经工业级光电介质转换模块（光纤交换机）连接至光纤链路，从而与加速器大厅屏蔽间内PLC子站进行通讯。
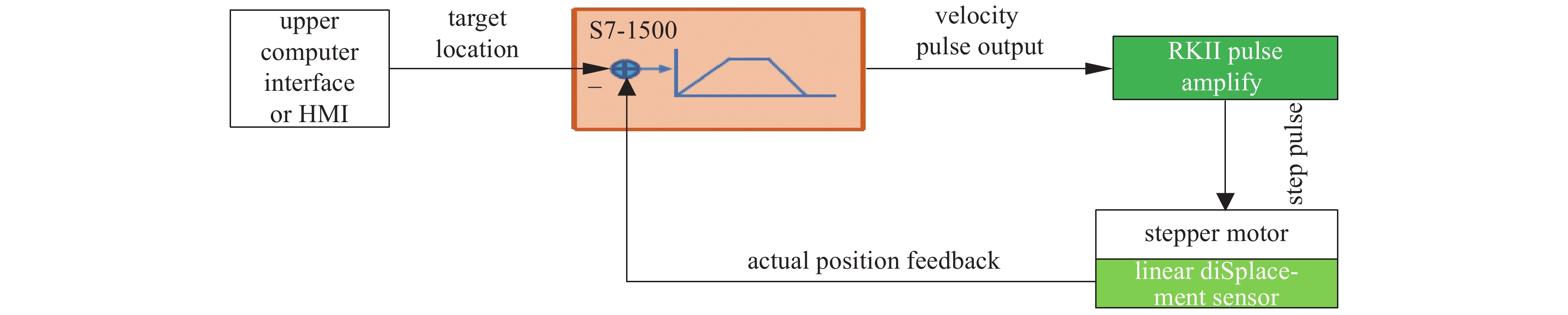
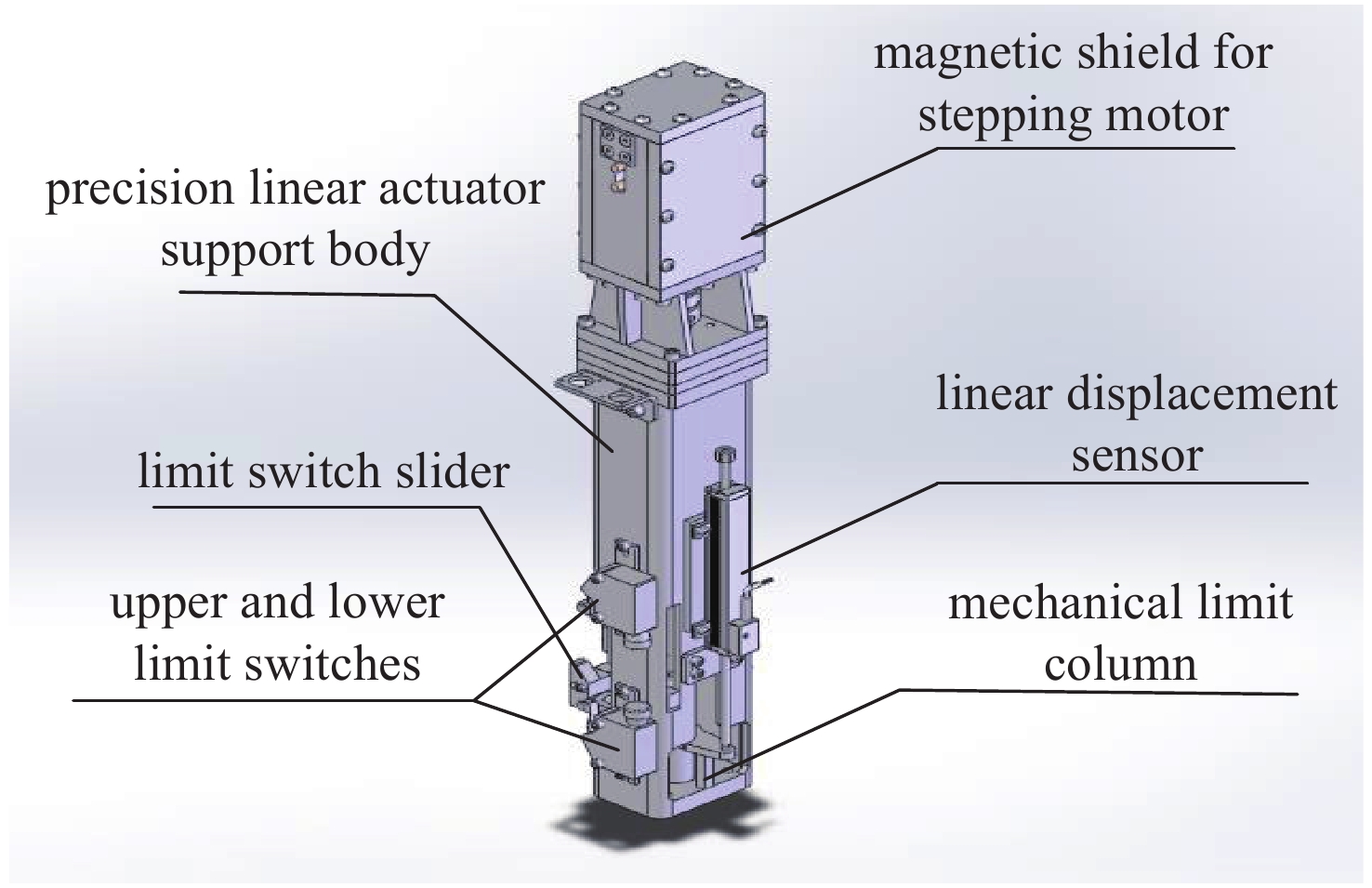
图 2 CYCIAE-230磁场调节棒驱动系统架构图Figure 2. Architecture diagram of trim-rod drive system on CYCIAE-230磁场调节棒定位运动控制采用基于PLC控制器加直线位移传感器负反馈闭环的方案，其原理示意图如图3。图4为磁场调节棒驱动系统机械结构示意图，结构紧凑、驱动力大、且可以工作于强磁场环境下。
图 3 CYCIAE-230磁场调节棒驱动控制原理图Figure 3. Control principle of trim-rod drive system on CYCIAE-230
图 4 CYCIAE-230磁场调节棒驱动机械结构示意图Figure 4. Schematic diagram of mechanical structure of trim-rod drive system on CYCIAE-2302.2 硬件选型方案
2.2.1 可编程控制器
可编程控制器选用德国西门子PLC S7-1516作为主控系统。该CPU的运动控制资源总量为2400个，Profinet接口传输速率100 Mbps，CPU最快位处理速度10 ns，编程语言LAD/FBD、STL、SCL和Graph。该CPU有强大运算能力和丰富的运动控制资源，利用其内置的运动定位功能，配合数个可接受脉冲序列速度指令的步进电机驱动器，实现对16根磁场调节棒的精确控制。
PLC子站选用高性能的西门子ET200MP系列产品。ET200MP远程IO站中布置了用于采集实际位置信号的模拟量输入模块，采集步进电机驱动器状态信号和限位开关信号的数字量输入模块，以及用于控制步进电机驱动器的数字量输出模块和TM PTO4定位功能模板。单个西门子TM PTO4模板可以通过脉冲输出方式控制4台步进电机驱动器。
2.2.2 精密直线执行器
精密直线执行器选用美国Thomson公司的PC32系列的电动缸，可以将步进电机的旋转运动转换为磁场调节棒的直线运动。PC32电动缸结构紧凑，最大动态负载可达3200 N，最大输入速度6000 rpm，重复定位精度±0.01 mm。此外，该精密直线执行器使用寿命长、维护要求低，非常适用于加速器的特殊场合。
2.2.3 直线位移传感器
直线位移传感器采用德国Novotechnik公司TR/TRS系列的电子尺，其采用电位计原理可以在强电离辐射环境中使用。电子尺的独立线性度可达到±0.05%，可重复性为0.002 mm，标准阻值1 kΩ或5 kΩ，使用寿命长、运行次数可达到
$1 \times {10^8}$ 次。由于其采用的材料及工艺的改进，上述直线电子尺可在−30～100 ℃的温度范围内正常工作，且温度系数极低，可保证磁场调节棒的定位精度[9]。位移传感器信号调节装置采用MUP160系列的信号转换器，零位和量程可调。线性度0.01%，温漂20 ppm/K，输入阻抗＞10 MΩ，允许连接阻抗≥700 Ω，就近连接传感器，信号在远距离传输时可以很好地保证信号传递的可靠性和抗干扰性。
3. 主要性能测试
3.1 定位精度
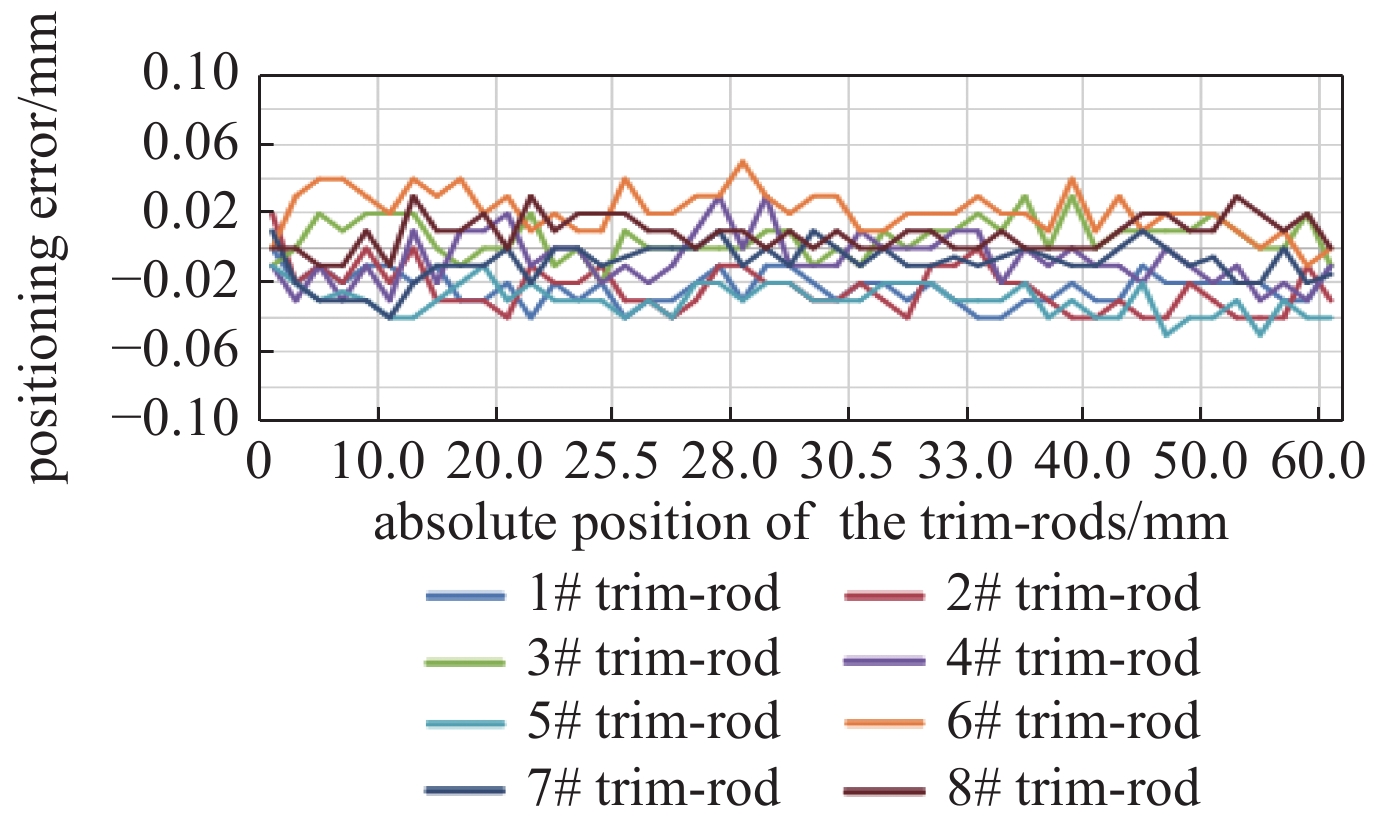
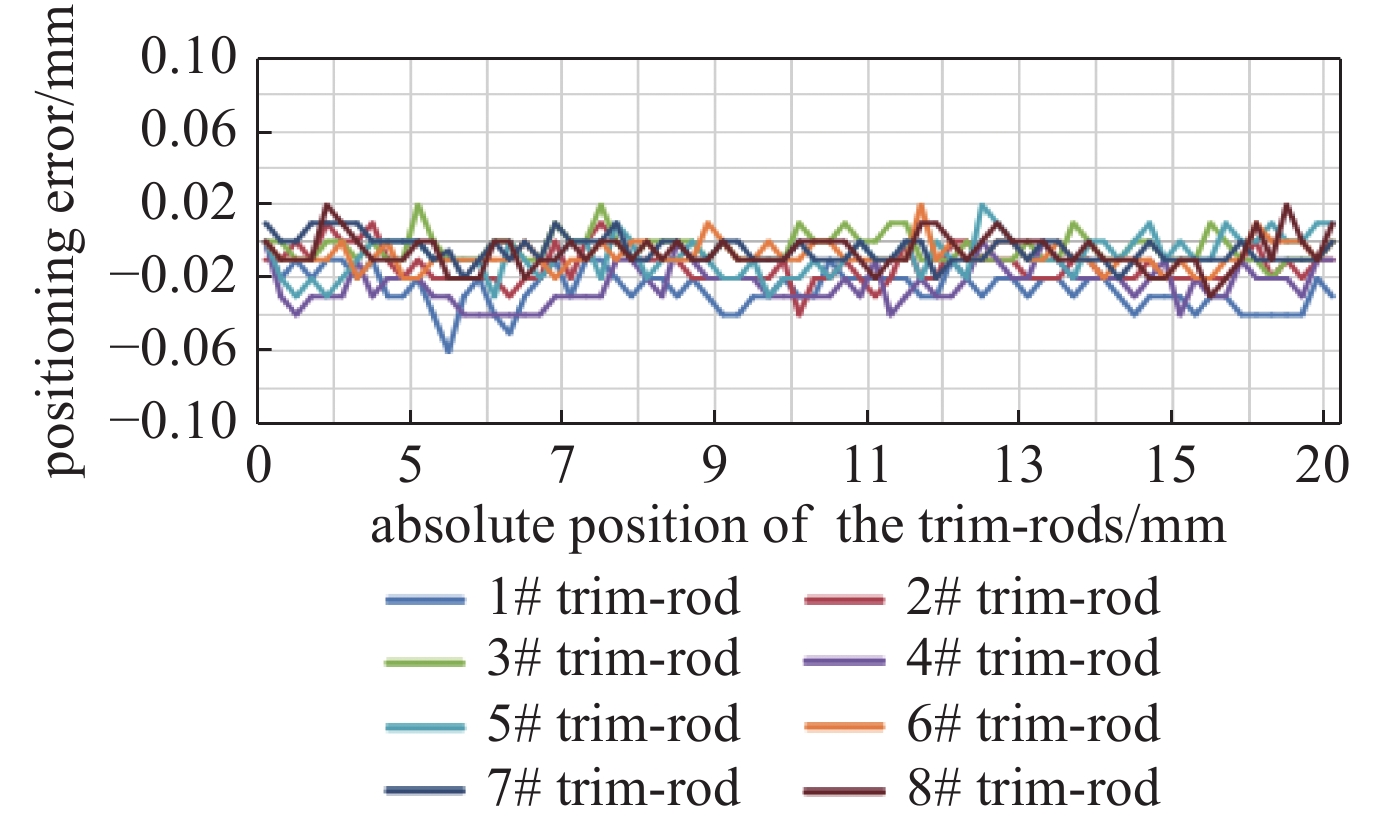
定位精度是磁场调节棒驱动系统最关键的指标之一，对中心区和引出区的每套磁场调节棒驱动系统的定位精度进行标定测试。引出区磁场调节棒的运动行程为60 mm，磁场调节棒全行程运动，每隔0.5 mm定位标定一次，各个磁场调节棒定位精度如图5所示。中心区磁场调节棒的运动行程为20 mm，磁场调节棒全行程运动，每隔0.2 mm定位标定一次，各个磁场调节棒定位精度如图6所示。在加速器未加磁场情况下标定测试结果表明，中心区和引出区所有磁场调节棒的定位精度均在0.05 mm以内，满足物理设计精度要求。
图 5 引出区磁场调节棒的定位精度Figure 5. Positioning accuracy of the trim-rods in extraction region3.2 磁场调节精度
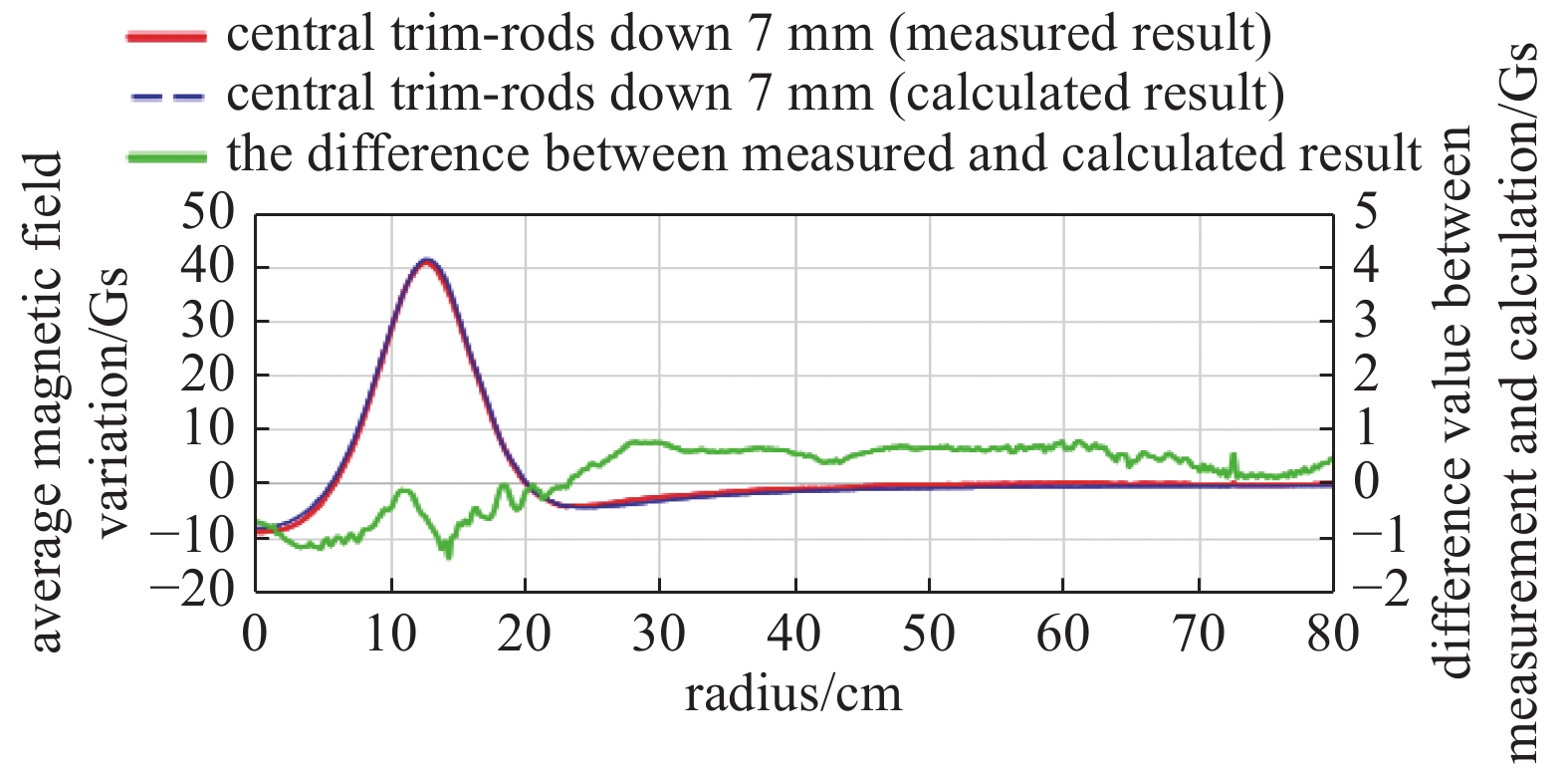
在加速器运行工况下，通过测量运动磁场调节棒后所引起的平均场变化来校准磁场调节棒的磁场调节精度。将230 MeV加速器超导线圈励磁至250 A，调节中心区的8根磁场调节棒，均向加速器中心平面运动7 mm，利用测磁仪测量分别测量调节磁场调节棒前后的主磁铁磁场强度。基于有限元模型的算法可计算移动调节棒带来的理论磁场变化[8]，与实际测量的磁场变化比较如图7所示。结果表明，通过控制系统反馈调节棒位置可以理论上较好地预期真实的磁场变化，这为通过调节棒优化束流物理提供了条件。
3.3 重复定位精度
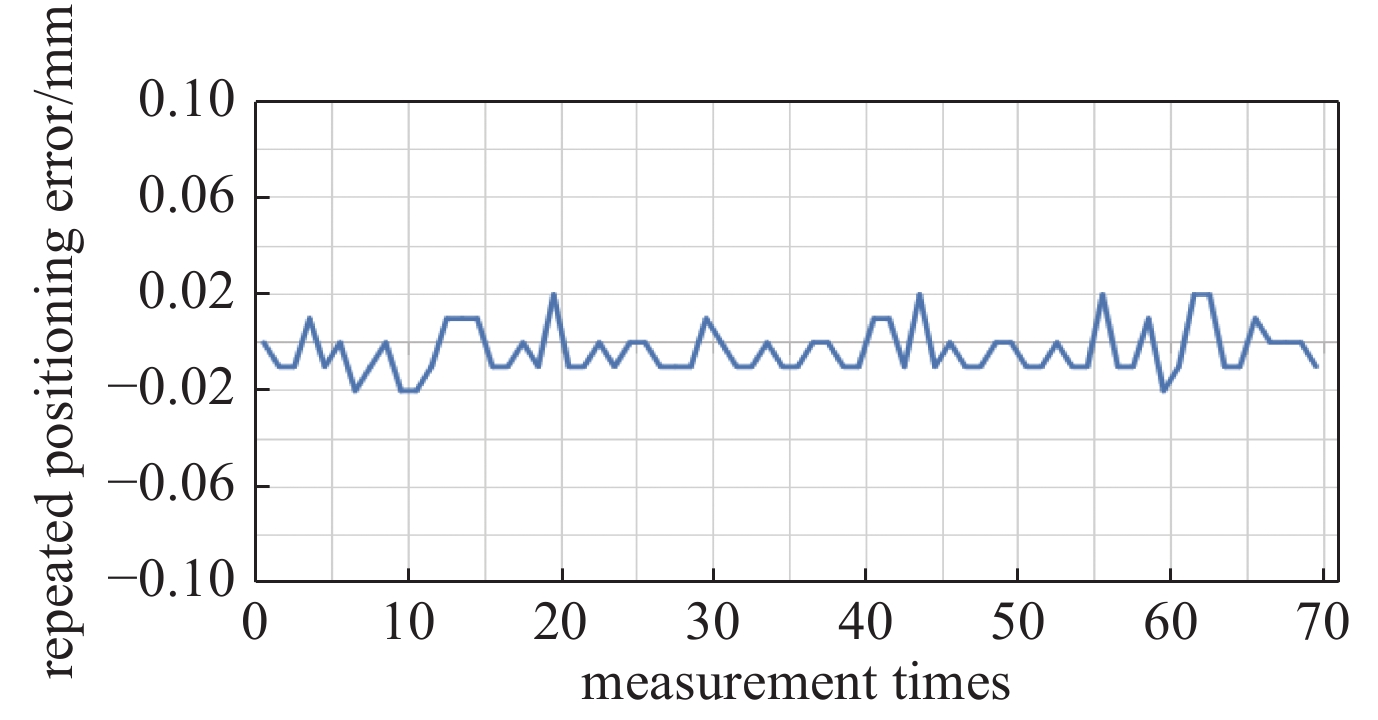
重复定位精度是磁场调节棒驱动系统的重要指标，通过反复将磁场调节棒运动到某一点，记录在该点的误差，反复测试了70次，其误差数据如图8所示。在加速器未加磁场情况下测试结果表明，该磁场调节棒驱动系统重复定位精度在±0.02 mm之内，满足物理设计指标要求。在加速器励磁状态下，由于加速器磁极表面磁场较强，千分表等金属测量仪器无法使用。从理论上进行受力分析，所有调节棒受力均一致，且在行程范围内受力变化不大，因而可以保证较好的重复定位精度。
3.4 电磁兼容测试
3.4.1 静电放电测试
对磁场调节棒驱动控制系统进行静电放电测试，分别在步进电机连续运行和步进电机停止不动时，利用静电放电发生器产生6 kV 1 Hz直流高压信号，加在机柜螺钉、门缝、散热风扇缝隙、机柜吊环等位置处观察步进电机运转是否抖动，上位测试界面上观察电子尺信号是否满足控制精度要求（0.1 mm）。
经测试：步进电机在连续运行和停止状态下，均未发现异常，上位测试界面电子尺信号波动在0.01 mm范围内，无其他异常显示。
3.4.2 电快速瞬变脉冲群测试
对磁场调节棒驱动控制系统进行电快速瞬变脉冲群测试，根据YY 0505-2012《医用电气设备第1-2部分：安全通用要求并列标准：电磁兼容要求和实验》测试电脉冲电压2000 V，频率5 kHz。将电子尺信号线缆、步进电机驱动电缆、步进电机抱闸线缆放置于耦合夹中，打开组合式抗扰度测试仪，设置测试参数，打开干扰信号进行测试。使步进电机处于连续运行，观察步进电机运动状态及上位界面电子尺信号。
经测试：步进电机运动正常，电子尺信号稳定，信号波动在0.01 mm范围内，无其他异常显示，满足YY 0505-2012/IEC 6060 1-1-2:2004标准要求。
3.4.3 浪涌抗扰度测试
对磁场调节棒驱动控制系统进行浪涌抗扰度测试，分别测试相地浪涌和相相浪涌。根据YY 0505-2012《医用电气设备第1-2部分：安全通用要求并列标准：电磁兼容要求和实验》相地浪涌测试参数：相地电压±2000 V，浪涌间隔时间1 min，持续10 min；相相浪涌测试参数：相相电压±1000 V，浪涌间隔时间1 min，持续30 min。将三相电源接入组合式抗扰度测试仪的电源输入端，组合式抗扰度测试仪输出端接驱动柜电源输入端。接线完成后，设置上述参数，打开浪涌信号进行测试。使步进电机处于连续运行，观察步进电机运动状态及上位界面电子尺信号。磁场调节棒驱动控制系统工作正常，步进电机运动正常，电子尺信号稳定，满足YY 0505-2012/IEC 6060 1-1-2:2004标准要求。
4. 结 论
在230 MeV超导回旋加速器运行过程中，需要运动磁场调节棒提供束流对中和束流引出所需磁场。为满足所有磁场调节棒的运动需要，研制了16套驱动系统装置，其运动控制采用PLC控制器和直线位移传感器负反馈闭环的方案。在实际工况下，运动定位精度达到0.05 mm，重复精度达到±0.02 mm，优于设计要求。
该驱动系统的研制，克服了在强电离辐射、高磁场强度、狭小安装空间的特殊环境中达到高定位精度和高重复精度的难点，对优化束流的径向进动，减小加速区域的相干振荡振幅，提高引出区的束流引出效率等具有重要意义。此外，对该系统进行了静电测试、电快速瞬变脉冲群测试和浪涌抗扰度测试，结果满足医用电气设备电磁兼容标准YY 0505-2012/IEC 6060 1-1-2:2004的要求。为后续230 MeV超导回旋加速器取得相关医疗设备认证，以用于癌症诊断和治疗打下了良好的基础。
-
图 3 不同介电常数的碳酸钡材料电压特性
Figure 3. Voltage characteristic of barium carbonate at different dielectric constant
图 4 不同介电常数的碳酸钡材料温度特性
Figure 4. Temperature characteristic of barium carbonate at different dielectric constant
图 5 单个环形脉冲形成线实验电路图
Figure 5. Experimental circuit diagram of single ring pulse forming line
-
[1] Mesyats G A, Korovin S D, Gunin A V, et al. Repetitively pulsed high-current accelerators with transformer charging of forming lines[J]. Laser and Particle Beams, 2003, 21: 197-209. [2] Smith I D. Induction voltage adders and the induction accelerator family[J]. Physical Review Special Topics—Accelerators and Beams, 2004, 7: 064801. doi: 10.1103/PhysRevSTAB.7.064801 [3] Rose D V, Welch D R, Oliver B V, et al. Power flow in a 7-cavity fast-rise LTD system[C]//Proc of the 14th IEEE International Pulsed Power Conference. 2003: 845-848. [4] Mayes J R. A compact Marx generator for the generation of high power microwaves[C]//High Power Microwave Conference. 2001. [5] Heffernan L K. A fast, 3 MV Marx generator for megavolt oil switch testing and integrated Abramyan network design[D]. Columbia: University of Missouri, 2005. [6] 孟志鹏, 杨汉武, 钱宝良, 等. 单级长脉冲LTD模块的设计及分析[J]. 高电压技术, 2009, 35(1): 69-74. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200901012.htmMeng Zhipeng, Yang Hanwu, Qian Baoliang, et al. Design and analysis of a single stage long pulse LTD module. High Voltage Engineering, 2009, 35(1): 69-74 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200901012.htm [7] Chen Y L, Neuber A A, Mankowski J, et al. Design and optimization of a compact, repetitive, high-power microwave system[C]//Beams Conference. 2000: 905-908. [8] Mayes J R, Mayes M G, Lara M B. A novel Marx generator topology design for low source impedance[C]//IEEE Pulsed Power Conference. 2005: 684-687. [9] Nunnally C, Lara M, Mayes J R, et al. A compact 700 kV erected pulse forming network for HPM applications[C]//IEEE Pulsed Power Conference. 2011: 1372-1376. [10] Mayes J R, Hatfield C W. Development of a sequentially switched Marx generator for HPM loads[C]//IEEE Pulsed Power Conference. 2009: 934-937. [11] 郝世荣, 谢卫平, 丁伯南, 等. Marx发生器驱动的电感储能型脉冲功率源[J]. 高电压技术, 2009, 35(3): 657-660. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200903040.htmHao Shirong, Xie Weiping, Ding Bonan, et al. Inductive energy storage pulsed power source energized by a Marx generator. High Voltage Engineering, 2009, 35(3): 657-660 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200903040.htm [12] 秦风, 宋法伦, 甘延青, 等. 模块化低阻抗紧凑型Marx发生器[J]. 强激光与粒子束, 2012, 24(4): 907-911. doi: 10.3788/HPLPB20122404.0907Qin Feng, Song Falun, Gan Yanqing, et al. Compact low-impedance Marx generator. High Power Laser and Particle Beams, 2012, 24(4): 907-911 doi: 10.3788/HPLPB20122404.0907 [13] 高景明, 刘永贵, 刘金亮, 等. 陡化前沿Marx发生器中开关过电压的研究[J]. 高电压技术, 2009, 35(1): 75-81. https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200901013.htmGao Jingming, Liu Yonggui, Liu Jinliang, et al. Investigation on over voltage of the spark gap switch in a wave erection Marx generator. High Voltage Engineering, 2009, 35(1): 75-81 https://www.cnki.com.cn/Article/CJFDTOTAL-GDYJ200901013.htm [14] 李志强, 杨建华, 张建德, 等. 紧凑重频PFN-Marx脉冲发生器[J]. 强激光与粒子束, 2016, 28: 015013. doi: 10.11884/HPLPB201628.015013Li Zhiqiang, Yang Jianhua, Zhang Jiande, et al. A compact repetitive PFN-Marx generator. High Power Laser and Particle Beams, 2016, 28: 015013 doi: 10.11884/HPLPB201628.015013 [15] Bluhm H. 脉冲功率系统的原理与应用[M]. 江伟华译. 北京: 清华大学出版社, 2008.Bluhm H. Pulsed power systems principles and applications. Jiang Weihua, Trans. Beijing: Tsinghua University Press, 2008 [16] Kong J A. Electromagnetic wave theory[M]. Beijing: Electronic Industries Press, 2003 [17] 王德生, 刘斌, 陈维, 等. 电极留边量与高压陶瓷电容器表面放电关系的研究[J]. 电工电能新技术, 2001, 20(2): 25-28. https://www.cnki.com.cn/Article/CJFDTOTAL-DGDN200102005.htmWang Desheng, Liu Bin, Chen Wei, et al. Advanced technology of electrical engineering and energy. Advanced Technology of Electrical Engineering and Energy, 2001, 20(2): 25-28 https://www.cnki.com.cn/Article/CJFDTOTAL-DGDN200102005.htm -
下载:
下载:
点击查看大图
计量
- 文章访问数: 1455
- HTML全文浏览量: 333
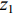
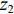
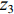
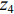
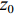
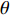
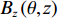
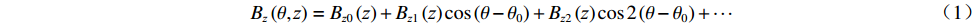
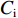
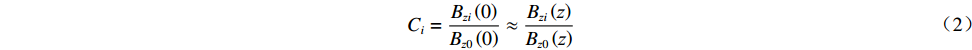
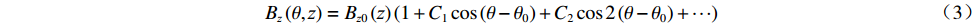
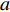
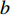
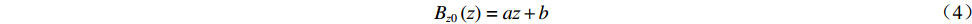
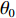
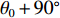
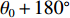
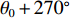
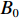
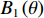
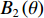
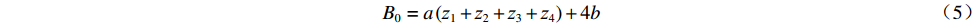
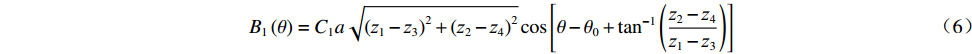
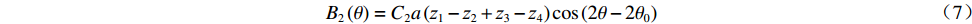
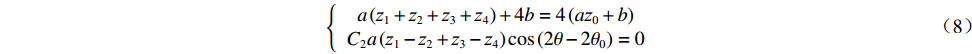
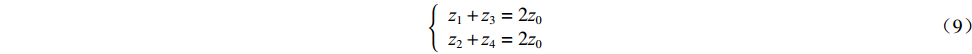
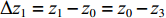
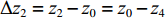
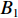
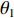
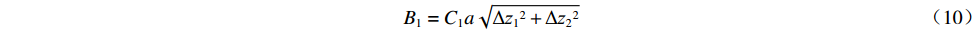
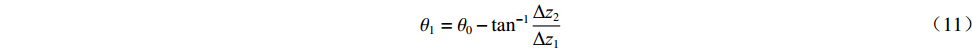
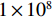
- PDF下载量: 270
- 被引次数: 0
