准方波脉冲形成网络的理论分析与设计

王传伟; 李洪涛

doi:10.11884/HPLPB201830.170392

准方波脉冲形成网络的理论分析与设计

doi: 10.11884/HPLPB201830.170392

王传伟^{1, 2,},
李洪涛^1, ,

1.
中国工程物理研究院流体物理研究所, 脉冲功率科学与技术重点实验室, 四川绵阳 621900
2.
中国工程物理研究院研究生院, 北京 100088

基金项目:

国家自然科学基金项目 61504127

国家自然科学基金项目 U1530128

中国工程物理研究院院长基金项目 YZJJLX2016002

详细信息

作者简介:
王传伟(1983－)，男，博士研究生，副研究员，从事固态脉冲技术及测控技术研究；250705799@qq.com

通讯作者:
李洪涛(1968－)，男，研究员，从事脉冲功率技术研究；lihongtao-ifp@caep.cn

中图分类号: TN784
计量
- 文章访问数: 1257
- HTML全文浏览量: 269
- PDF下载量: 254
- 被引次数: 0
出版历程
- 收稿日期: 2017-10-10
- 修回日期: 2017-11-26
- 刊出日期: 2018-03-15

Theoretical analysis and design of the trapezoidal pulse forming network

Wang Chuanwei^{1, 2
,},
Li Hongtao^{1
, ,}

1.
Key Laboratory of Pulsed Power, Institute of Fluid Physics, CAEP, P.O. Box 919-107, Mianyang 621900, China
2.
Graduate School of China Academy of Engineering Physics, Beijing 100088, China

摘要

摘要: 针对微波驱动源、固态调制器等对宽平顶脉冲源的应用需求，开展了基于脉冲形成网络输出准方波的理论研究与分析设计。首先采用Prony算法获得准方波波形的解析表达式，然后基于最佳一致逼近的优化控制思路，列出极点控制方程，采用数值方法求解非线性方程组，获得优化波形参数。在此基础上采用阻抗函数匹配的算法求解出脉冲形成网络的元件参数初始值，根据工程设计的实际情况舍弃部分参数并对个别参数进行优化后，获得最终的元器件参数。通过理论分析与数值模拟相结合的方法，系统地给出了获取长脉宽、低纹波准方波脉冲形成网络的设计方法以及设计准则。该方法可用于设计任意阶低纹波系数的准方波脉冲源，也可用于设计其他输出波形要求的脉冲源。
- 准方波 /
- 脉冲形成网络 /
- Prony算法 /
- 最佳一致逼近 /
- 阻抗匹配设计 /
- 低纹波
Abstract: For the application requirements of the high voltage pulse generator based on the pulse forming network(PFN) in the microwave driver and the solid-state modulator, the theory of the PFN with the trapezoidal pulse output was developed. First, the analytical expression of the trapezoidal pulse was obtained by the Prony algorithm. Secondly, the waveform parameters were optimized by using the best uniform approximation algorithm based on the equations of the optimal control with the maximum and minimum of the output wave, and solving these nonlinear equations with the Newton iteration method or other numerical methods. Then, the initial parameters of the PFN were worked out with the method of impedance matching. The final components parameters were obtained by rejecting some secondary parameters and adjusting a few of the main parameters. The method and criteria of the design for a PFN with the low ripple trapezoidal pulse output were proposed by theoretical analysis and numerical simulation. The results show that the proposed method can be used to design the PFN with any order and low ripple, and it can be used to design not only the pulse source with trapezoidal pulse output, but also the pulse sources with other pulse output.
- trapezoidal pulse /
- pulse forming network /
- Prony algorithm /
- best uniform approximation /
- impedance matching design /
- low ripple

HTML全文

图 1 理想方波及Prony级数拟合准方波波形

Figure 1. Rectangular pulse and trapezoidal pulses fitted by Prony series

下载: 全尺寸图片幻灯片

图 2 最佳一致逼近优化波形

Figure 2. Waveforms obtained by best uniform approximation algorithm

下载: 全尺寸图片幻灯片

图 3 基于脉冲形成网络(PFN)的脉冲发生器电路模型

Figure 3. Circuit model of pulse generator based on pulse forming network(PFN)

下载: 全尺寸图片幻灯片

图 4 常用脉冲形成网络(PFN)电路构型

Figure 4. Circuits of commonly used PFN

下载: 全尺寸图片幻灯片

图 5 五级B型PFN仿真电路

Figure 5. Simulation circuit of 5-stage B-type PFN

下载: 全尺寸图片幻灯片

图 6 未优化电路元件参数时输出脉冲波形

Figure 6. Output pulses without optimization of element parameters

下载: 全尺寸图片幻灯片

图 7 优化电路元件参数后输出脉冲波形

Figure 7. Output pulses with optimization of element parameters

下载: 全尺寸图片幻灯片

表 1 Prony算法直接拟合所得复振幅和复频率

Table 1. Results of amplitudes and frequencies obtained by Prony algorithm

A₁	A₂	A₃	A₄	A₅	A₆	A₇	A₈	A₉	A₁₀
0.004 199 -0.014 816i	0.004 199 +0.014 816i	0.020 346 -0.033 943i	0.020 346 +0.033 943i	0.067 039 -0.070 089i	0.067 039 +0.070 089i	0.238 64 -0.221 1i	0.238 64 +0.221 1i	-0.330 22 -2.036 1i	-0.330 22 +2.036 1i

α₁	α₂	α₃	α₄	α₅	α₆	α₇	α₈	α₉	α₁₀
-0.051 922 +30.519i	-0.051 922 -30.519i	-0.217 84 +23.345i	-0.217 84 -23.345i	-0.537 27 +16.189i	-0.537 27 -16.189i	-1.125 6 +9.109 6i	-1.125 6 -9.109 6i	-2.226 3 +2.600 5i	-2.226 3 -2.600 5i

下载: 导出CSV

表 2 最佳一致逼近优化所得复振幅

Table 2. Results of amplitudes obtained by best uniform approximation algorithm

ε	A₁	A₂	A₃	A₄	A₅	A₆	A₇	A₈	A₉	A₁₀
0.005	0.004 213 -0.008 190i	0.004 213 +0.008 190i	0.016 645 -0.020 462i	0.016 645 +0.020 462i	0.059 499 -0.051 987i	0.059 499 +0.051 987i	0.230 59 -0.196 64i	0.230 59 +0.196 64i	-0.310 95 -2.007 5i	-0.310 95 +2.007 5i
0.001	0.002 448 4 -0.003 337 2i	0.002 448 4 +0.003 337 2i	0.0130 59 -0.012 782i	0.013 059 +0.012 782i	0.053 507 -0.040 342i	0.053 507 +0.040 342i	0.224 76 -0.178 59i	0.224 76 +0.178 59i	-0.293 78 -1.984 5i	-0.293 78 +1.984 5i

下载: 导出CSV

表 3 直接匹配求解出的五级B型脉冲形成网络参数(ε=0.001)

Table 3. Parameters of devices in 5- stage B-type PFN with ε=0.001

L₁	L₂	L₃	L₄	L₅	C₁	C₂	C₃	C₄	C₅
0.121 8	0.058 6	0.059 6	0.068 4	0.095 3	0.066 7	0.057 9	0.063 0	0.077 6	0.145 0

R₁	R₂	R₃	R₄	R₅	G₁	G₂	G₃	G₄	G₅
0.019 5	-0.007 4	0.000 6	0.000 6	-0.004 2	0.014 1	-0.001 9	0.001 1	-0.000 9	-0.012 4

下载: 导出CSV

表 4 五级B型脉冲形成网络优化后参数

Table 4. Optimized parameters of devices in 5- stage B-type PFN

ε	L₁	L₂	L₃	L₄	L₅	C₁	C₂	C₃	C₄	C₅
0.005	0.102 4	0.056 2	0.061 4	0.070 9	0.098 6	0.059 3	0.058 8	0.065 8	0.081 1	0.151 4
0.001	0.126 7	0.058 6	0.059 6	0.068 4	0.095 3	0.066 7	0.057 9	0.063 0	0.077 6	0.145 0

下载: 导出CSV

表 5 五级B型脉冲形成网络优化后输出脉冲波形特征参数

Table 5. Features of output pulses in simulation circuit of Fig. 5

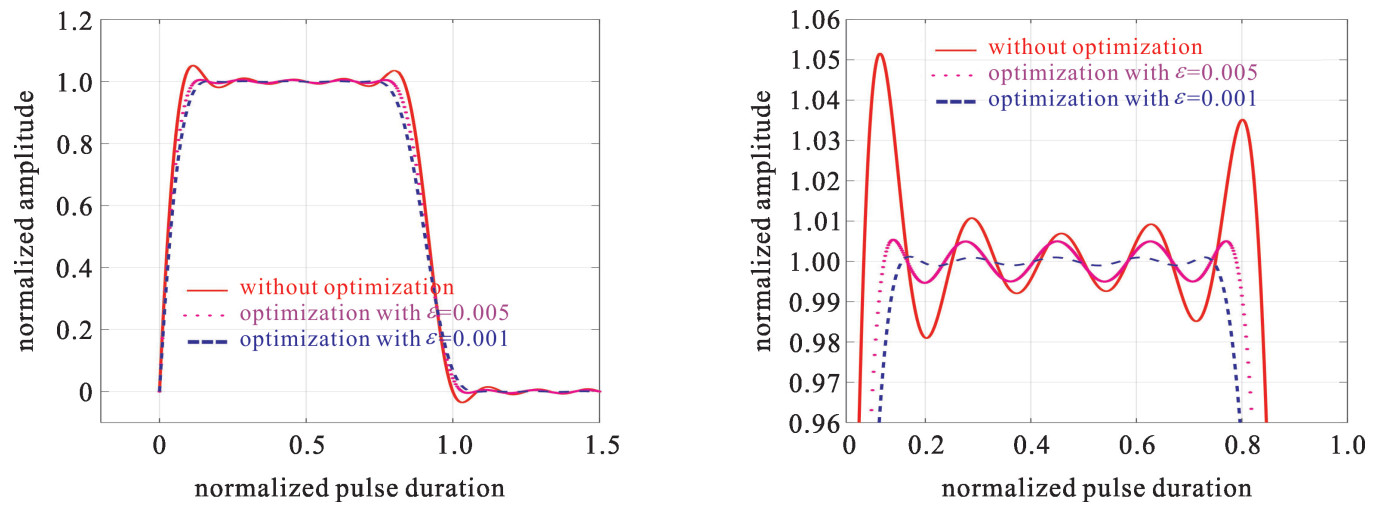
ε(designed)	t_ri(10%~90%)	t_fi(90%~10%)	t_w1(10%~10%)	t_w2(100%~100%)	ε(simulated)
0.005	0.070	0.137	0.964	0.670	0.006 8
0.001	0.089	0.169	0.988	0.584	0.001 3

下载: 导出CSV

参考文献(12)

[1]	龙霞锋, 刘永贵. Marx型脉冲形成网络的研究[J]. 中国物理C, 2008, 32 (s1): 274-276. https://www.cnki.com.cn/Article/CJFDTOTAL-KNWL2008S1092.htm Long Xiafeng, Liu Yonggui. Investigation of Marx-PFN. Chinese Physics C, 2008, 32 (s1): 274-276 https://www.cnki.com.cn/Article/CJFDTOTAL-KNWL2008S1092.htm
[2]	李志强, 杨建华, 张建德, 等. 紧凑重频PFN-Marx脉冲发生器[J]. 强激光与粒子束, 2016, 28: 015013. doi: 10.11884/HPLPB201628.015013 Li Zhiqiang, Yang Jianhua, Zhang Jiande, et al. A compact repetitive PFN-Marx generator. High Power Laser and Particle Beams, 2016, 28: 015013 doi: 10.11884/HPLPB201628.015013
[3]	黄华, 范植开, 马乔生, 等. 长脉冲相对论速调管放大器的初步实验研究[J]. 强激光与粒子束, 2002, 14 (6): 915-919. http://www.hplpb.com.cn/article/id/1409 Huang Hua, Fan Zhikai, Ma Qiaosheng, et al. Progress on a long pulse relativistic klystron amplifier. High Power Laser and Particle Beams, 2002, 14 (6): 915-919 http://www.hplpb.com.cn/article/id/1409
[4]	田景昌, 宋小泉, 李自良. HPM脉冲形成网络的理论分析与计算[J]. 飞行器测控学报, 2003, 22 (3): 72-74. Tian Jingchang, Song Xiaoquan, Li Ziliang. Theoretical analysis and calculation of HPM pulse forming network. Journal of Spacecraft TT&C Technology, 2003, 22 (3): 72-74
[5]	吴谨, 万重怡. 紫外预电离TE(A)CO₂激光器自持辉光放电的阻抗计算[J]. 激光杂志, 2002, 23 (2): 15-17. https://www.cnki.com.cn/Article/CJFDTOTAL-JGZZ200202005.htm Wu Jin, Wan Chongyi. Calculation of the glow discharge impedance of a UV-preionized self-sustained TE(A)CO₂ laser. Laser Journal, 2002, 23 (2): 15-17 https://www.cnki.com.cn/Article/CJFDTOTAL-JGZZ200202005.htm
[6]	刘锡三. 高功率脉冲技术[M]. 北京: 国防工业出版社, 2005: 116-119. Liu Xishan. High pulsed power technology. Beijing: National Defense Industry Press, 2005: 116-119
[7]	王朋, 李名加, 康强, 等. L型脉冲形成网络的仿真与实验研究[J]. 强激光与粒子束, 2013, 25 (9): 2461-2465. doi: 10.3788/HPLPB20132509.2461 Wang Peng, Li Mingjia, Kang Qiang, et al. Simulation and experimental research on L-type pulse forming network. High Power Laser and Particle Beams, 2013, 25 (9): 2461-2465 doi: 10.3788/HPLPB20132509.2461
[8]	程道国. 脉冲形成网络设计中的若干问题[J]. 现代电子, 1998, 63 (2): 22-27. https://www.cnki.com.cn/Article/CJFDTOTAL-LDKJ199802005.htm Cheng Daoguo. Some problem in design of pulse forming network. Modern Electronics, 1998, 63 (2): 22-27 https://www.cnki.com.cn/Article/CJFDTOTAL-LDKJ199802005.htm
[9]	李洪涛, 王传伟, 王凌云, 等. 500 kV全固态Marx发生器[J]. 强激光与粒子束, 2012, 24 (4): 917-920. doi: 10.11884/HPLPB202133.200223 Li Hongtao, Wang Chuanwei, Wang Lingyun, et al. 50 kV all-solid-state Marx generator. High Power Laser and Particle Beams, 2012, 24 (4): 917-920 doi: 10.11884/HPLPB202133.200223
[10]	徐利治, 王仁宏, 周蕴时. 函数逼近的理论与方法[M]. 上海: 上海科学技术出版社, 1983: 246-250. Xu Lizhi, Wang Renhong, Zhou Yunshi. The theory and method of function approximation. Shanghai: Shanghai Scientific and Technical Publishers, 1983: 246-250
[11]	李庆杨, 王能超, 易大义. 数值分析[M]. 4版. 北京: 清华大学出版社, 2001: 78-83, 287-288. Li Qingyang, Wang Nengchao, Yi Dayi. Numerical analysis. 4th ed. Beijing: Tsinghua University Press, 2001: 78-83, 287-288
[12]	Smith P W. Transient electronics: pulsed circuit technology[M]. New York: John Wiley & Sons Ltd, 2011: 107-136.