Numerical simulation of influence of target dimension and laser spot size on laser impulse
-
摘要: 采用二维雷诺平均N-S方程，数值模拟研究了大气条件下短脉冲激光与固体靶相互作用所产生等离子体的动力学过程。采用k-ε两方程模型用于湍流的数值模拟，分别利用ROE格式和二阶中心格式对对流通量和粘性通量进行离散处理；用高斯-赛德尔隐式格式对方程进行时间推进求解。数值模拟给出了激光引发靶蒸气等离子体侧向膨胀、稀疏等二维流体动力学过程的物理图像，讨论了靶与光斑尺寸对脉冲激光冲量的影响。结果表明，不同宽度固体靶受到的激光冲量有很大差异，固体靶宽度越大，受到的激光冲量也越大。Abstract: The plasma flow field of solid target in atmosphere under impulse laser irradiation was computed. The flow is governed by the 2-D Reynolds averaged Navier-Stokes (NS) equations. The k-ε turbulence model was used for turbulence simulations. To split the viscosity flux and the convective flux of the NS equations, the second order central scheme and the ROE scheme were adopted respectively. With the implicit Gauss-Seidel scheme, the code was advanced in time. The 2-D hydrokinetics process of laser plasma was presented in this paper by numerical simulation. The influence of target dimension and laser spot size on laser impulse was discussed. The results indicated that laser impulse increases generally with target dimension.
-
Key words:
- numerical simulation /
- laser impulse /
- target /
- laser spot size
-
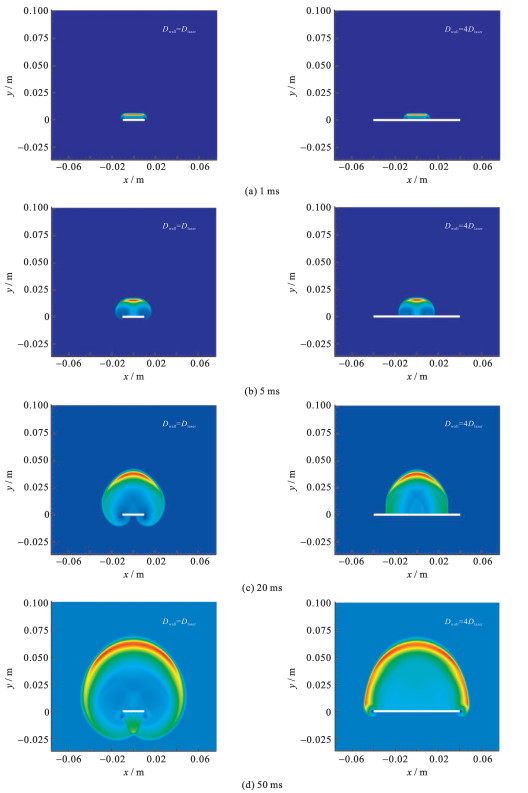
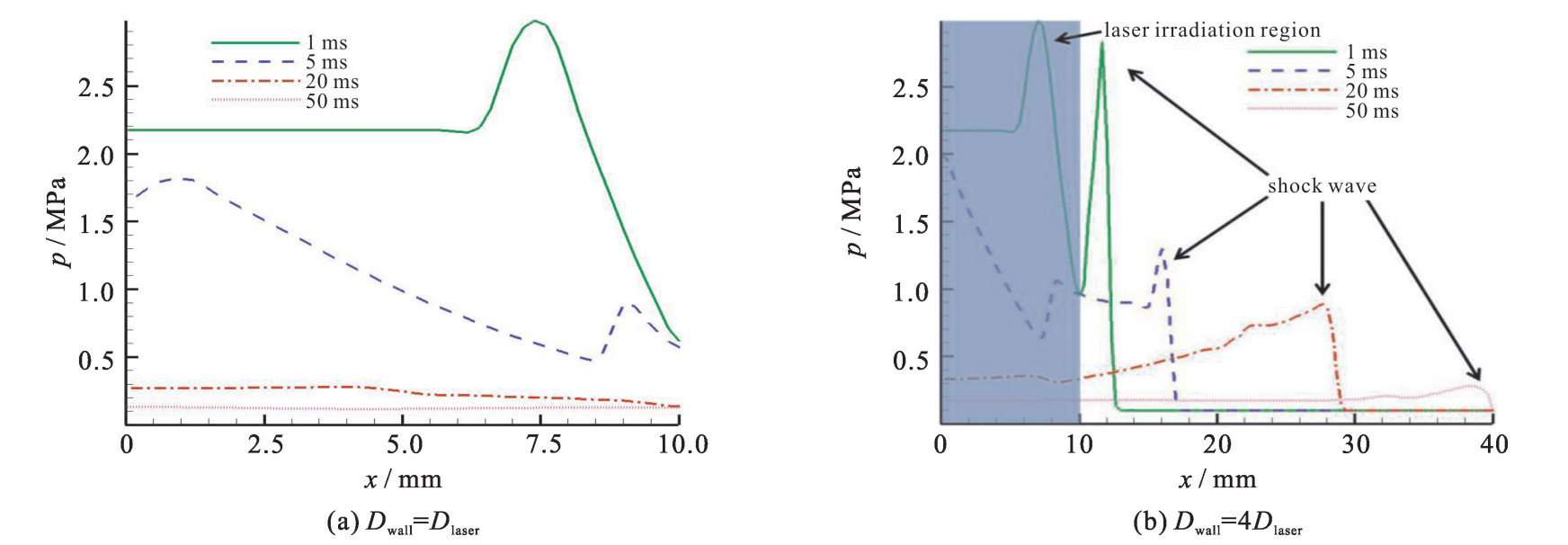
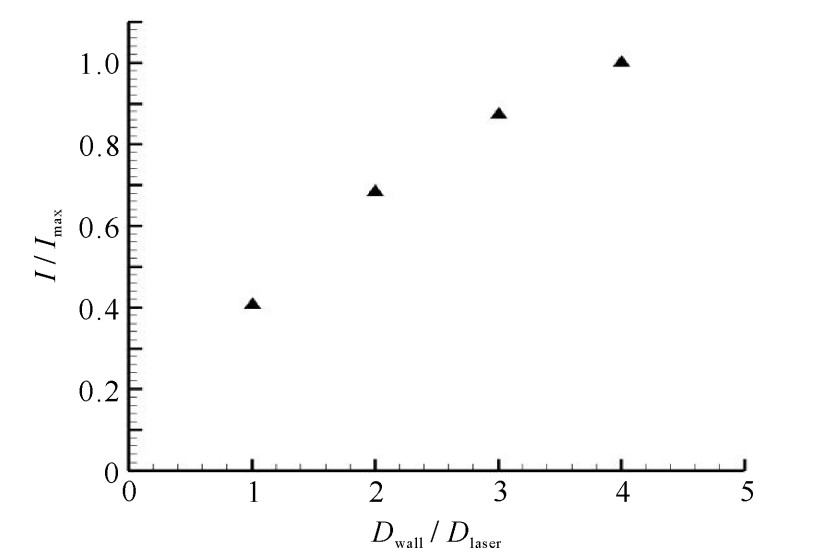
[1] 孙承纬. 激光辐照效应[M]. 北京: 国防工业出版社, 2002.Sun Chengwei. Laser irradiation effects. Beijing: National Defense industry Press, 2002 [2] Phipps C R, Turner T P, Harrison R F, et al. Impulse coupling to targets in vacuum by KrF, HF, and CO2, single-pulse lasers[J]. Journal of Applied Physics, 1988, 64(3): 1083-1096. doi: 10.1063/1.341867 [3] Nehls M, Edwards D, Gray P. Ablative laser propulsion using multi-layered material systems[C]//Proc of 33rd AIAA Plasma Dynamics and Lasers Conference. 2002: 20-23. [4] Bass M, Nassar M A, Swimm R T. Impulse coupling to aluminum resulting from ND: glass laser irradiation induced material removal[J]. J Appl Phys, 1987, 61(3): 1137-1144. [5] Pakhmov A V, Lin J, Kenneth A H. Effect of air pressure on propulsion with TEA CO2[C]//Proc of SPIE. 2004, 5448: 1017-1027. [6] 章玉珠, 王广安, 沈中华, 等. 等离子体屏蔽和稀疏波对冲量耦合系数的影响[J]. 强激光与粒子束, 2007, 19(4): 585-588. http://www.hplpb.com.cn/article/id/3146Zhang Yuzhu, Wang Guang'an, Shen Zhonghua, et al. Influences of plasma shielding and rarefaction wave on impulse coupling coefficient. High Power Laser and Particle Beams, 2007, 19(4): 585-588 http://www.hplpb.com.cn/article/id/3146 [7] Phipps C, Luke J, Funk D, et al. Laser impulse coupling at 130 fs[J]. Applied Surface Science, 2006, 252(13): 4838-4844. doi: 10.1016/j.apsusc.2005.07.079 [8] 英敏菊, 王潇潇, 程伟, 等. 激光烧蚀靶材蒸发波模型的气体动力学与冲量耦合系数计算[J]. 北京师范大学学报(自然科学版), 2015, 51(1): 40-44. https://www.cnki.com.cn/Article/CJFDTOTAL-BSDZ201501011.htmYing Minju, Wang Xiaoxiao, Cheng Wei, et al. Calculation of gas dynamic parameters and impulse-coupling coefficient for laser ablation of a target. Journal of Beijing Normal University(Natural Science), 2015, 51(1): 40-44 https://www.cnki.com.cn/Article/CJFDTOTAL-BSDZ201501011.htm [9] 张黎, 贺佳, 谭福利. 激光加热金属板流固耦合数值模拟[J]. 强激光与粒子束, 2011, 23(4): 866-869. http://www.hplpb.com.cn/article/id/5128Zhang Li, He Jia, Tan Fuli. Numerical simulation of metal plates under laser irradiation based on fluid-solid coupling. High Power Laser and Particle Beams, 2011, 23(4): 866-869 http://www.hplpb.com.cn/article/id/5128 -
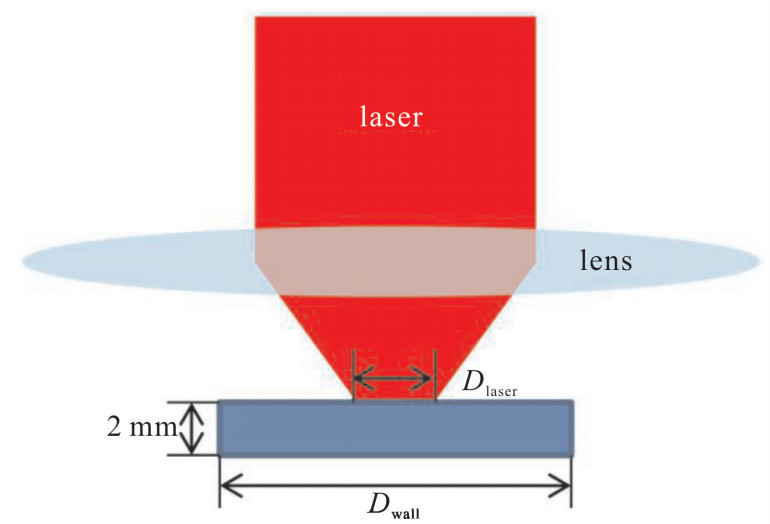
下载:
点击查看大图
图(6)
计量
- 文章访问数: 1094
- HTML全文浏览量: 165
- PDF下载量: 167
- 被引次数: 0
