Uncertainty analysis of industrial CT linear size measurement
-
摘要: 针对加速器工业CT线性尺寸测量的不确定度评定,建立了工业CT尺寸测量模型,对测量中不确定度的主要来源进行分析,基于测量不确定度表示指南(GUM)法对工业CT线性尺寸测量不确定度评定进行研究。以6 MeV高能工业CT系统尺寸测量为例,分析了长度样块线性尺寸测量各主要的不确定度分量,对尺寸测量的不确定度进行评定,最终得出具有包含概率为0.99的扩展不确定度为0.09 mm,结果体现了工业CT尺寸测量的精度和可靠性,为工业CT尺寸测量结果的可靠度提供参考依据。Abstract: The evaluation of the uncertainty of accelerator industrial CT has always been one of the difficulties in the research and application of industrial CT. In order to evaluate the uncertainty of linear dimension measurement of accelerator industrial CT, an industrial CT size measurement model was established, and the main sources of uncertainty in the measurement were analyzed. Based on the Guide to the Expression of Uncertainty in Measurement (GUM) method, the evaluation of the uncertainty of industrial CT linear dimension was studied. Taking 6 MeV high-energy industrial CT system size measurement as an example, the main uncertainty components of linear dimension measurement of length samples were analyzed, and the uncertainty of the dimension measurement was evaluated. The result is an extended uncertainty of 0.09 mm with an inclusion probability of 0.99, which reflects the accuracy and reliability of industrial CT dimensional measurements. This paper provides a reference for the reliability of the size measurement results of industrial CT.
-
Key words:
- accelerator /
- industrial CT /
- dimension measurement /
- uncertainty assessment /
- expanded uncertainty
-
表 1 采样点的灵敏系数
Table 1. Sensitivity of the sampling points
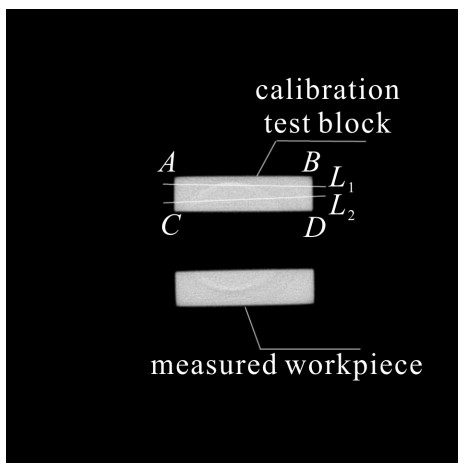
measuring point a transfer factor $ {\left( {\frac{{\partial g}}{{\partial {a_i}}}} \right)}$ e transfer factor $ {\left( {\frac{{\partial g}}{{\partial {e_i}}}} \right)}$ c transfer factor $ {\left( {\frac{{\partial g}}{{\partial {c_i}}}} \right)}$ d transfer factor $ {\left( {\frac{{\partial g}}{{\partial {d_i}}}} \right)}$ s transfer factor $ {\left( {\frac{{\partial g}}{{\partial {s_i}}}} \right)}$ 1 -0.373 -0.414 -0.404 0.414 0.827 2 -0.280 -0.322 -0.313 0.322 0.642 3 -0.305 -0.347 -0.339 0.347 0.692 4 -0.258 -0.300 -0.290 0.300 0.596 5 -0.319 -0.378 -0.328 0.378 0.724 6 -0.352 -0.390 -0.377 0.390 0.778 7 -0.765 -0.688 -0.586 0.688 1.399 8 -0.659 -0.631 -0.560 0.631 1.268 9 -0.406 -0.390 -0.329 0.390 0.784 10 -0.336 -0.360 -0.332 0.360 0.716 表 2 校准试块的测量值
Table 2. Measured values of the test block
No. calibration value, xcal/mm measurement, yi/mm 1
2
3
4
5
6
7
8
9
109.001
9.001
9.001
9.001
9.001
9.001
9.001
9.001
9.001
9.0019.039
9.021
9.025
9.027
9.025
9.036
9.016
9.038
9.029
9.024表 3 工业CT尺寸测量的不确定分量汇总表
Table 3. Summary of uncertain components for industrial CT dimensional measurements
input quantity Xi estimated value xi standard uncertainty u(xi) probability distribution sensitivity coefficient uncertainty component/μm l 10.034 mm 0.018 mm normal 1 18 Δt 0 1.15 ℃ rectangular 0.115 μm·℃-1 0.132 δr 0 0.014 mm rectangular 1 14 δv 0 0.462 μm rectangular 1 0.462 b 0.027 mm 0.027 mm normal -1 27 -
[1] 庄天戈. CT理论与算法[M]. 上海: 上海交通大学出版社, 1992.Zhuang Tiange. CT theory and algorithm. Shanghai: Shanghai Jiao Tong University Press, 1992 [2] 张朝宗, 郭志平. 工业CT技术和原理[M]. 北京: 科学出版社, 2009.Zhang Chaozong, Guo Zhiping. Industrial CT technology and principles. Beijing: Science Press, 2009 [3] Badakhshannoory H, Saeedi P. Automatic liver segmentation from CT scans using multi-layer segmentation and principal component analysis[J]. Advances in Visual Computing, 2010, 6454: 342-350. [4] 张俊哲. 无损检测技术及其应用[M]. 北京: 科学出版社, 2010.Zhang Junzhe. Nondestructive testing technology and its application. Beijing: Science Press, 2010 [5] Hsieh J. 计算机断层成像技术——原理、设计、伪像和进展[M]. 北京: 科学出版社, 2006: 1-71.Hsieh J. Computed tomography, principle, design, artifacts and recent advances. Beijing: Science Press, 2006: 1-71 [6] European Committee for Standardization. ISO/DIS 15708-1, Non-destructive testing—Radiation methods—computed tomography—Part1: Principle, equipment and samples[S]. Geneva: International Organization for Standardization, 2016. [7] 平雪良, 周儒荣, 党耀国. 未知自由曲面三坐标测量新方法[J]. 机械科学与技术, 2005, 24(4): 491-493. doi: 10.3321/j.issn:1003-8728.2005.04.032Ping Xueliang, Zhou Rurong, Dang Yaoguo. A new method of coordinate measurement for unknown free-form surfaces. Mechanical Science and Technology for Aerospace Engineering, 2005, 24(4): 491-493 doi: 10.3321/j.issn:1003-8728.2005.04.032 [8] De Chiffre L, Carmignato S, Kruth J P. Industrial applications of computed tomography[J]. CIRP Annals-Manufacturing Technology, 2014, 63: 655-677. doi: 10.1016/j.cirp.2014.05.011 [9] 刘艳萍, 马燕, 张晶, 等. 工业技术在炸药装药质量检测中的应用[J]. 计测技术, 2013, 33: 69-72. https://www.cnki.com.cn/Article/CJFDTOTAL-HKJC2013S1023.htmLiu Yanping, Ma Yan, Zhang Jing, et al. Application of industrial technology in quality inspection of explosive charge. Metrology & Measurement Technology, 2013, 33: 69-72 https://www.cnki.com.cn/Article/CJFDTOTAL-HKJC2013S1023.htm [10] Bartscher M, Ehrig K, Goebbels J, et al. Dimensional control of micro components with synchrotron computed tomography[C]//AIP Conference Proceedings. 2010, 1221(1): 164-171. [11] Bartscher M, Hilpert U, Fiedler D. Determination of the measurement uncertainty of computed tomography measurements using a cylinder head as an example[J]. Technisches Messen, 2008, 75(3): 178-186. doi: 10.1524/teme.2008.0822 [12] Batenburg K J, Sijbers J. Adaptive thresholding of tomograms by projection distance minimization[J]. Pattern Recognition, 2009, 42(10): 2297-2305. doi: 10.1016/j.patcog.2008.11.027 [13] Bartscher M, Krystek M. Method for a traceable geometry assessment of arbitrarily shaped sculptured surfaces[C]//10th Int Symp on Measurement and Qaulity Control(ISMQC). 2010. [14] Dewulf W, Kiekens K, Tan Y. Uncertainty determination and quantification for dimensional measurements with industrial computed tomography[J]. CIRP Annals—Manufacturing Technology, 2013, 62: 535-538. doi: 10.1016/j.cirp.2013.03.017 [15] 胡林福. 测量不确定度与误差的区别[J]. 质量技术监督研究, 2009(1): 55-56. https://www.cnki.com.cn/Article/CJFDTOTAL-FJXX200901017.htmHu Linfu. Differences between measurement uncertainty and error. Quality and Technical Supervision Research, 2009(1): 55-56 https://www.cnki.com.cn/Article/CJFDTOTAL-FJXX200901017.htm [16] 胡巧开, 邓真丽, 付勤. 不确定度及其应用探讨[J]. 湖北师范学院学报, 2010, 30(2): 104-109. https://www.cnki.com.cn/Article/CJFDTOTAL-HBSF201002024.htmHu Qiaokai, Deng Zhenli, Fu Qin. Discussion on uncertainty and its application. Journal of Hubei Normal University, 2010, 30(2): 104-109 https://www.cnki.com.cn/Article/CJFDTOTAL-HBSF201002024.htm -




 下载:
下载:




