Molecular dynamics simulations of shock response for nano-structure foamed gold
-
摘要: 采用分子动力学计算程序对纳米结构泡沫金(Au)的冲击响应进行了模拟，得到了不同疏松度条件下泡沫Au的冲击压缩特性。通过获取不同势函数条件下实密Au的冲击Hugoniot关系以及泡沫结构稳定性测试选取适合描述Au泡沫冲击过程中原子的相互作用势。采用密堆积球壳的方式建立泡沫Au的初始构型。通过改变空心球壳的尺寸得到不同疏松度的稳定的泡沫Au结构。对泡沫Au的冲击过程进行分子动力学模拟，获得了不同疏松度泡沫Au在不同冲击压缩强度下的热力学状态参数。将模拟结果与已有的状态方程数据库以及疏松物质冲击压缩模型进行比较，结果表明，计算和理论模型给出的结果仍然存在明显的差异性，亟需通过进一步实验研究来验证模拟计算和理论模型结果的可靠性。
-
关键词:
- 纳米Au结构稳定性 /
- Au泡沫 /
- 分子动力学模拟 /
- 泡沫冲击Hugoniot曲线
Abstract: Different embeded-atom method potentials of gold were used in molecular dynamics simulation for shocked solid gold. Comparison between the simulation results and the experiment data of Hugoniot state for gold has been carried out. The potentials whose corresponding simulating shocked Hugoniot data are consistent with theoretical prediction were used in subsequent foamed gold simulations. The initial configuration of foamed gold has been constructed by means of randomly accumulating sphere shells in the simulation box. Three kinds of configuration have been obtained via changing the thickness, outer-radius of the sphere shell and potentials. Hugoniot states of porous polycrystal gold with 3-dimensional nanostructure under shock compression have been simulated by means of molecular dynamics(MD) method. Comparison between simulated results with porous equation of state(EOS) model and existing EOS database for Au has been done. The discrepancy suggests that experiments for the state of porous gold are necessary to verify the theory and the simulation method for porous gold. -
疏松材料，如泡沫、气凝胶等，由于具有能量吸收率高、绝热性能良好等优点，不仅在军事、民用工业生产中广泛应用，在高能量密度物理领域[1]也具有重要的研究价值。比如通过获取不同疏松度(实密材料与疏松材料初始密度的比值)材料的冲击Hugoniot关系来扩展材料状态方程实验研究的参数范围[2]，在Z装置(Z-pinch)实验中使用泡沫材料作为“动态”黑腔的内柱层材料，提高加载均匀性进而提高内爆效率[3]，在激光惯性约束聚变(ICF)研究中将泡沫材料用作黑腔的腔壁材料以提高X射线转化效率和减少腔壁能量漏失等[3-4]。因此，对泡沫材料的冲击压缩特性研究有着重要的科学意义和实用价值。相对于实密材料，疏松材料在冲击压缩条件下的热效应更加明显[5]，显著的热效应可能使得材料在冲击条件下的膨胀效应超过其压缩效应，出现材料压缩度随着冲击压强增大而降低的“反常”冲击压缩特性[5]。为了获得疏松材料的冲击Hugoniot关系，可采用不同的理论或计算模型。一方面，传统的状态方程数据库如SESAME，QEOS等给出了不同材料温度、密度参数条件下的热力学状态参数数据库，可以利用Hugoniot关系式插值获得材料在不同初始密度即不同疏松度条件下的冲击Hugoniot曲线；另一方面，从实密材料的冲击Hugoniot关系出发，基于不同的假设，目前也发展了一系列用于预测的疏松材料冲击Hugoniot曲线的理论模型，如吴强和经福谦基于三项式物态方程，从等压路径出发，发展的W-J模型[6]以及耿华运等人在W-J模型的基础上，进一步考虑了热电子对于压强和比内能的贡献而得到的Geng HY模型[7]。除此以外，采用分子动力学计算的方法，基于牛顿力学模拟冲击波作用条件下原子、分子的运动，也可以直接得到材料在冲击波作用下的热力学状态参量，从而得到材料的冲击Hugoniot关系。采用分子动力学计算还能够针对疏松材料的冲击压缩过程，进一步研究材料的孔穴形状、尺寸等结构特征参数对冲击响应的影响[8-9]。本文以ICF黑腔物理研究关注的重点材料泡沫Au[10]为主要研究对象，采用分子动力学计算，获得泡沫Au材料在不同疏松度条件下的冲击Hugoniot曲线，和不同理论模型预测的结果进行比较，为进一步实验研究提供理论基础。
1. 模拟方法
采用分子动力学计算程序LAMMPS[11]和嵌入原子势函数(EAM)[12]，建立三维原子体系模拟一维冲击加载条件下的材料响应。模拟体系在X方向采用非周期性边界条件，YZ方向选用周期性边界条件。整个模拟体系沿-X方向以一定初始速度碰撞反射墙，碰撞发生后，在体系中产生沿+X方向传播的稳定冲击波，通过调节体系初始碰撞速度来改变冲击波的强度。通过一维面元分析[13]得到X方向面元应力和粒子速度随时间和空间的演化过程。对稳定冲击波后物理量求平均，得到波后的应力和物质的粒子速度；分析冲击波界面位置随时间的变化获得冲击波速度。进而通过冲击波关系式可以得到冲击波后的密度。
实验室制备泡沫Au通常具有空心球壳堆积的微观构型[14]，本文针对这种球壳构型进行分子动力学建模，建立了具有纳米结构的多晶泡沫Au模型：在给定的模拟体系内密堆积空心球壳，以每一个球壳的球心为中心，通过随机转动一定的角度来决定球壳上面心立方(fcc)Au原子晶格的取向，通过改变球壳的外径大小来改变泡沫Au体系的疏松度。
2. 模拟结果及讨论
2.1 势函数的选取及泡沫Au原子体系的稳定性
目前国际上采用的Au原子EAM势函数有多种[15-21]，势函数因其所研究的内容不同，其参数的侧重点也有所差异。Y.Liao等人通过模拟实密材料的冲击压缩特性，并和已有的冲击Hugoniot实验结果对比，通过对比的一致性好坏来判定该势函数用于疏松材料冲击过程模拟的适用性[22]。本文也采用此方法选择用于模拟泡沫Au冲击响应的势函数。
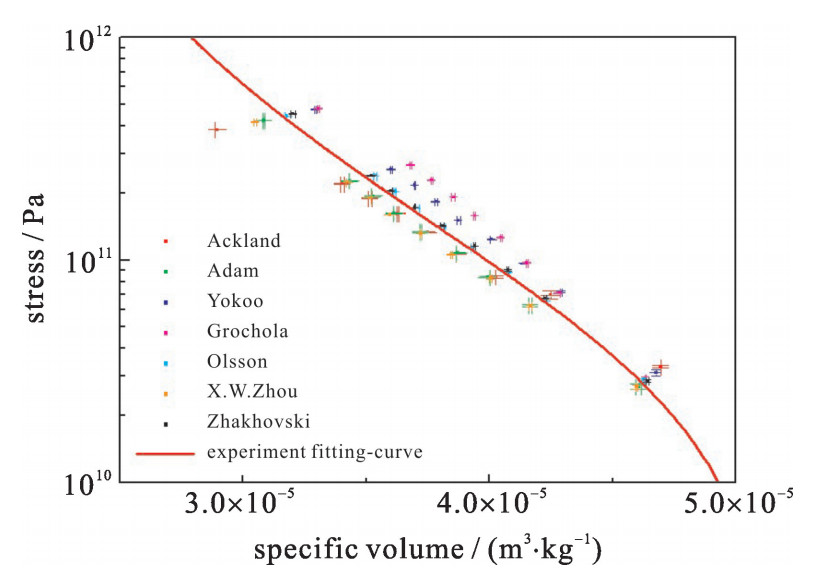
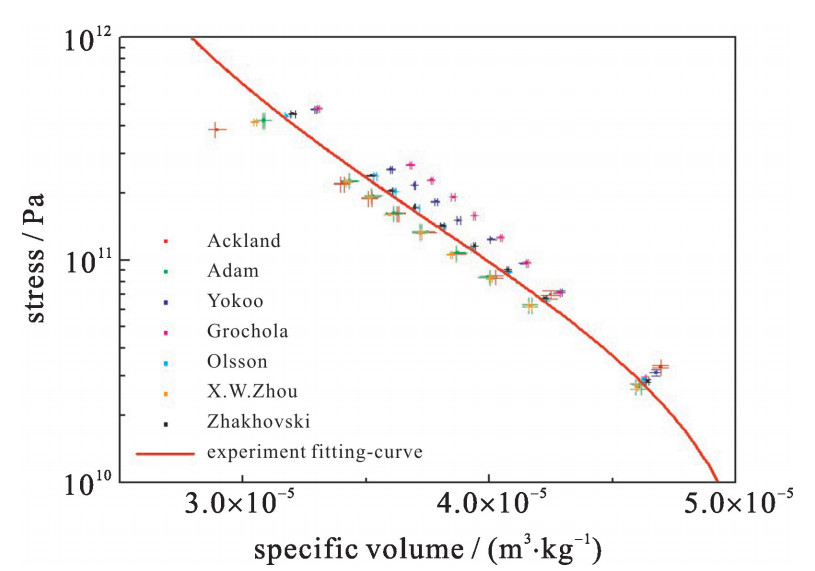
图 1给出了采用不同EAM模型模拟得到的实密Au的冲击Hugoniot关系及已有的实验结果拟合数据。分子动力学计算中，模拟体系在XYZ三个方向上包含的晶胞数分别为300，20和20。通过改变体系的初始速度(-0.4~-3 km/s)，得到一系列的冲击压缩状态。实验结果采用Manabu Yokoo等人测量的实密Au的Hugoniot数据[23]，他们给出580 GPa以内的冲击速度-粒子速度的线性拟合关系为D=C0+λu，其中，C0=2.995 km/s，λ=1.621。从图中可以看出，由Olsson[15]以及Zhakhovskii[14]提出的EAM势函数模型的模拟结果与实验结果在模拟参数范围内的一致性明显优于其他势函数给出的结果。比如冲击强度大约为100 GPa时，Olsson的势函数给出的模拟结果与实验拟合曲线之间密度的相对偏差小于0.4%，Zhakhovskii势函数的模拟结果相对偏差小于0.3%，而其他势函数的结果的相对偏差均大于2%。上述结果表明这两种势函数模型更适用于描述冲击条件下Au原子间的相互作用。
图 1 不同Au原子EAM势函数模拟实密Au冲击Hugoniot关系与实验拟合曲线对比Figure 1. Comparison between theory experiment fitting curve and simulated shock Hugoniot curve for solid gold by using different embedded atom method(EAM) potentials进一步采用上述两种势函数模型测试其用于泡沫Au时模拟体系的稳定性。同时，球壳的外径D0和球壳厚度d作为构建模型的输入参数，它们对结构稳定性也有一定的影响。
首先，固定球壳的外径D0=8 nm，考虑Au的晶格常数约为0.408 nm，选取在球壳的径向分别包含1，2和3个晶格结构，则对应的取球壳的厚度分别为d=0.5 nm，0.9 nm和1.3 nm，测试球壳厚度和势函数对于稳定性的影响。对以上三种构型分别使用两种势函数在弛豫400 ps后分析泡沫体系的稳定性。
当采用Olsson等人提出的势函数时，球壳状泡沫构型会消失或变形。比如球壳厚度为1.3 nm的体系弛豫后的原子分布如图 2(a)所示，其中绿色为面心立方(fcc)晶格，红色为六方密堆(hcp)晶格，从图中已经无法得到泡沫材料的初始球状构型，泡沫球发生破裂，部分原子初始的fcc晶体结构也在弛豫结束后更倾向于hcp结构。更小球壳厚度的构型(d=0.5 nm，0.9 nm)弛豫后的结果与图 2(a)相似。该结果表明在该势函数下模拟的不同厚度的泡沫Au原子构型并不稳定。采用Zhakhovskii势函数弛豫后得到体系构型表明：随球壳厚度的增大，体系趋于稳定。其中，厚度为0.5 nm的结构弛豫后结构消失，与图 2(a)类似；图 2(b)是球壳厚度为0.9 nm弛豫后的结构，该体系在弛豫后结构发生了一定的变形；图 2(c)是球壳厚度为1.3 nm弛豫后的结果，该体系与初始构型基本一致，且体系的势能几乎不再变化，体系达到稳定状态。
图 2 不同初始原子构型分子动力学弛豫后结果(YZ平面)。其中(a)为Olsson势函数弛豫后的构型，(b-e)为Zhakhovskii势函数弛豫后的构型Figure 2. Nano-structure after energy minimization (view of YZ-plane). Image (a) is the energy minimization result by using Olsson potential, while images (b-e) is the results by using Zhakhovskii potential进一步测试球壳外径对于稳定性的影响。固定球壳厚度d=1.3 nm，改变球壳外径D0=16 nm和20 nm。同样对这两种构型分别使用上述两种势函数在弛豫400 ps后分析其稳定性。当采用Olsson势函数时，两种构型的结构都消失，弛豫后的构型与图 2(a)类似。当采用Zhakhovskii势函数时，弛豫后的构型几乎不变，如图 2(d)~(e)所示。对这两种体系的势能分析表明它们的势能几乎不再变化，体系达到稳定状态。
上述模拟结果表明，在本文采用的纳米尺度泡沫结构参数条件下，使用Olsson势函数都会导致初始结构消失或变形，无法得到稳定的Au泡沫体系用于进一步的冲击响应研究。这可能和Olsson势函数更适合描述单晶中Au原子之间的相互作用[15]，并不适用于多晶泡沫Au原子体系建模；当采用Zhakhovskii势函数时，模拟结果表明空心球壳的厚度影响泡沫Au体系的稳定性(图 2(b)~(c))，球壳的外径对球壳结构体系几乎没有影响(图 2(c)~(e))。进一步分析图 2(c)~(e)三种构型的疏松度，发现在确定的球壳厚度的情况下，体系的疏松度随着球壳的外径的增大而增加。在后续的冲击响应的分子动力学模拟中，我们将采用Zhakhovskii势函数模型，将球壳厚度设定为1.3 nm，通过改变球壳的外径来获得不同疏松度条件下泡沫Au的冲击压缩特性。
2.2 泡沫Au的冲击响应
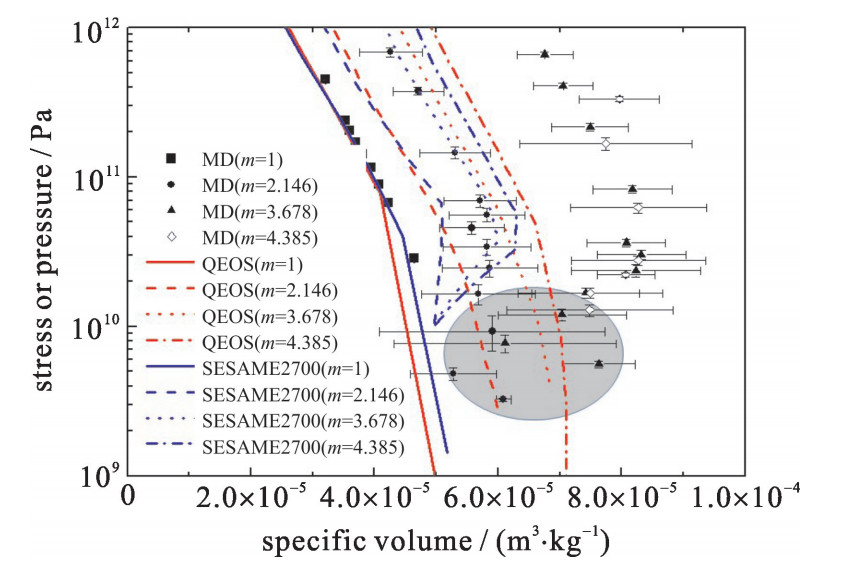
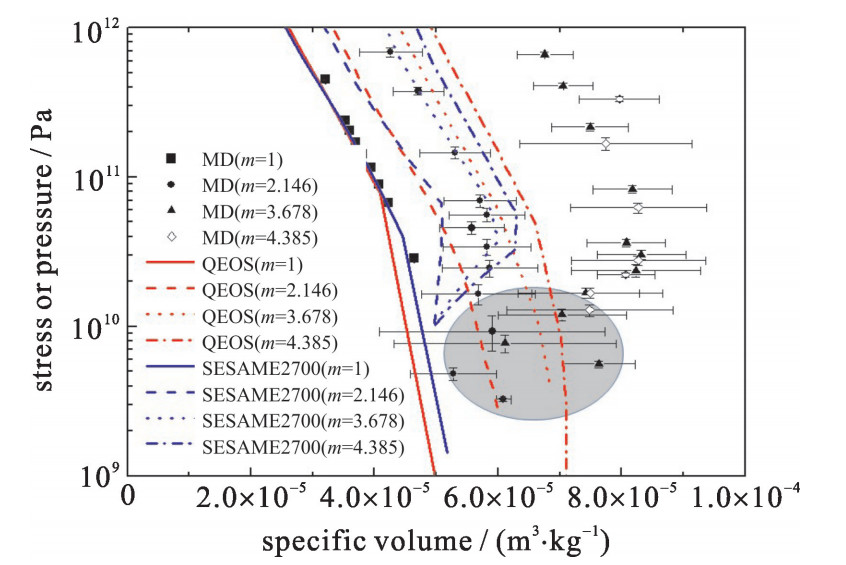
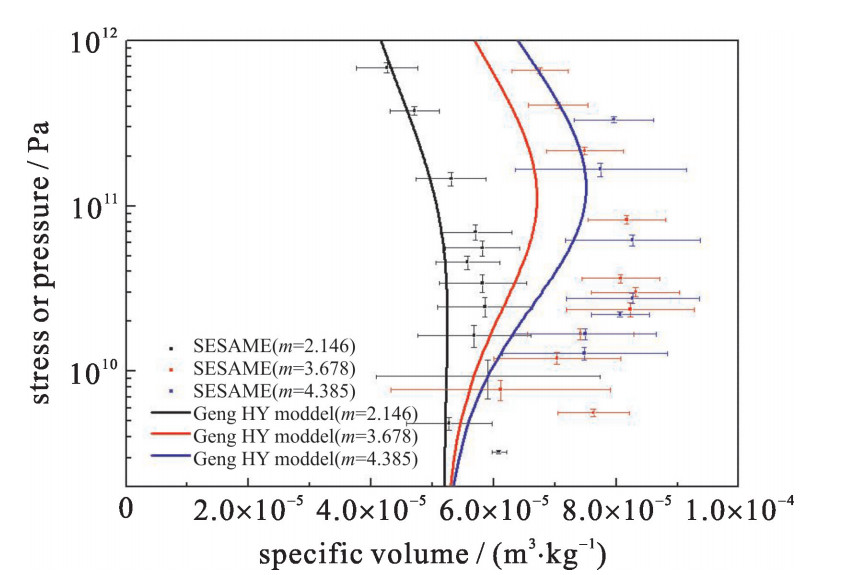
采用Zhakhovskii势函数进行泡沫Au冲击压缩特性分子动力学计算，计算所采用泡沫结构参数如表 1所示，相同球壳厚度条件下通过改变球壳外径分别得到了三种不同疏松度(m=2.146，3.678，4.385)的泡沫Au构型。模拟不同疏松度构型在不同强度冲击波下的响应，得到了波后应力与比容的关系。将不同疏松度条件下的计算结果与物态方程数据库QEOS，Sesame2700给出的结果进行比较，结果如图 3所示。
表 1 泡沫Au模型的参数表Table 1. Parameters of foamed gold for shock response simulationinitial thickness of shell d/nm initial outer-radius of shell D0/nm porosity/m atom numbers simulation box size nm 1.3 8 2.146 2 429 272 1777 nm×222 nm×222 nm 1.3 16 3.678 5 671 490 2701 nm×360 nm×360 nm 1.3 20 4.385 7 445 416 2702 nm×450 nm×450 nm 
图 3 泡沫Au的冲击Hugoniot分子动力学模拟结果与QEOS和SESAME的对比Figure 3. Comparison between shock Hugoniot simulation for foamed Au with QEOS and SESAME dataHodge等人的研究结果表明对于开孔的纳米疏松Au的屈服强度小于4 GPa[24]。在本文的主要模拟压强区域内，强度效应相比于应力的分量σxx为可忽略小量。因此，本文将一维应力σxx与EOS数据库中的压强直接比较。图 3中实心正方形、实心圆、实心三角和空心圆分别代表了疏松度为1，2.146，3.678和4.385的模拟结果，其中黑色为模拟结果，红色表示QEOS数据库的结果，蓝色为SESAME的结果。从图中可以看到，分子动力学计算给出的泡沫材料的冲击压缩状态存在比较明显的统计不确定度，这主要是由于泡沫材料中复杂的波系相互作用难以使系统在较大的特征空间尺度和较小的时间尺度内实现热力学平衡，并且面元分析选取的空间尺度只有0.5 nm，所以热力学参数的空间分布存在明显的涨落。对比分析分子动力学模拟和QEOS，SESAME数据库给出的结果表明，当m=1时，即实密材料，分子动力学模拟和QEOS，SESAME模型给出的结果一致性很好，相同压强(约100 GPa)条件下的密度偏差在1%左右，表明几种模型都可以准确描述实密Au冲击过程的热力学状态；而随着泡沫疏松度的增大，不同模型间的差异逐渐增大。其中QEOS和SESAME模型给出的结果差异增幅较小，当m=4.385时，两个模型之间的差异只增加5%左右，而分子动力学计算结果除在冲击压强较低的条件下和QEOS模型给出的结果有小部分区域吻合较好(图中阴影部分)以外，和QEOS和SESAME数据库给出的结果差异非常明显，当m=2.146时，和QEOS，SESAME结果的相对密度偏差在15%左右；当m=3.678时，偏差增加到30%左右；当m=4.385时，相对偏差在25%左右。从数据的变化趋势来看，分子动力学计算和SESAME模型给出的结果均在低于100 GPa左右的压强条件下表现为随冲击强度增加而压缩度降低的趋势。
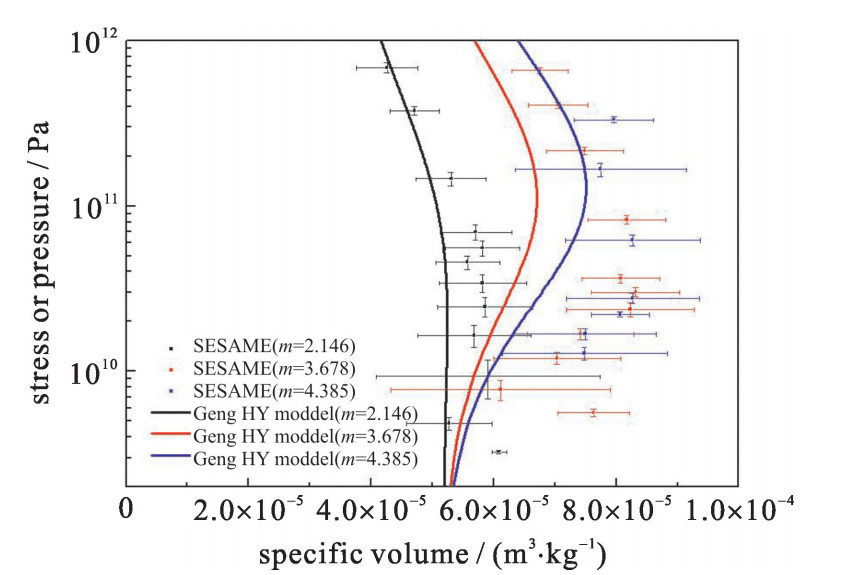
进一步将分子动力学计算结果与耿华运等人发展的疏松材料冲击Hugoniot理论模型进行比较，其结果如图 4所示。其结果表明，分子动力学模拟得到的Hugoniot曲线与Geng HY模型的预测结果的趋势是相同的，但存在一定的差异。这种差异会随着疏松度和冲击强度变化而变化，在疏松度为3.678时两者的偏差最大(80 GPa时约为18%)，疏松度为2.146时两者的偏差最小(80 GPa时约为10%)；在低于100 GPa的较低冲击强度条件下，两者的差异相对于100 GPa以上的结果差异更明显。
图 4 模拟结果与Geng HY模型预测曲线的对比Figure 4. Comparison between simulation results and prediction values by Geng HY model通过对泡沫Au体系的模拟，得到了不同疏松度条件下的泡沫Au构型的冲击Hugoniot关系。相比目前已有的状态方程数据库模型以及基于实密材料冲击Hugoniot曲线给出的疏松材料的冲击Hugoniot模型，尽管在预测实密材料或者初始密度接近常实密材料的冲击Hugoniot关系时多模型之间具有很好的一致性，但随着初始密度远离实密材料的密度时，不同模型预测的结果差异明显。因此，考虑到泡沫Au材料在ICF研究中的重要应用，进一步开展实验研究来获得不同疏松度条件下的冲击Hugoniot关系，从而验证目前广泛采用的如SESAME，QEOS一类状态方程数据库在预测泡沫材料冲击压缩状态的准确性，进一步完善状态方程理论模型显得尤为重要。另一方面，由于泡沫材料的冲击压缩曲线可以有效放大不同理论模型之间的差异，从状态方程理论模型的实验验证角度，采用疏松度材料开展冲击压缩实验研究可能会降低模型验证对实验精度的需求，从而减小实验研究的难度。
3. 结论
本文采用分子动力学的方法来研究不同疏松度条件下的泡沫Au冲击压缩特性。通过随机密堆积球壳的方法建立三维纳米结构的多晶泡沫Au模型，变换势函数、球壳外径以及球壳厚度获得了疏松度为2~4的泡沫Au稳定构型。对这些稳定构型进行了冲击压缩特性的模拟，并将模拟得到的Hugoniot关系与QEOS，SESAME数据库以及Geng HY模型进行比较。结果表明，对于泡沫Au材料，不同方法给出的冲击Hugoniot曲线存在明显的差异性，这种差异会随着疏松度的增加而变得明显。考虑到泡沫Au材料在ICF研究中的重要应用，需进一步开展泡沫Au材料的冲击压缩实验研究校验现有的状态方程理论模型。
致谢: 感谢天河二号提供的技术服务支持，感谢顶峰多尺度科学研究所的罗胜年老师以及蔡洋博士、简武荣博士对本工作的帮助和建议，感谢物理总体组郑建华在研究中给予的帮助，感谢中物院流体物理研究所耿华运关于模型的讨论指导。 -
图 1 不同Au原子EAM势函数模拟实密Au冲击Hugoniot关系与实验拟合曲线对比
Figure 1. Comparison between theory experiment fitting curve and simulated shock Hugoniot curve for solid gold by using different embedded atom method(EAM) potentials
图 2 不同初始原子构型分子动力学弛豫后结果(YZ平面)。其中(a)为Olsson势函数弛豫后的构型，(b-e)为Zhakhovskii势函数弛豫后的构型
Figure 2. Nano-structure after energy minimization (view of YZ-plane). Image (a) is the energy minimization result by using Olsson potential, while images (b-e) is the results by using Zhakhovskii potential
图 3 泡沫Au的冲击Hugoniot分子动力学模拟结果与QEOS和SESAME的对比
Figure 3. Comparison between shock Hugoniot simulation for foamed Au with QEOS and SESAME data
图 4 模拟结果与Geng HY模型预测曲线的对比
Figure 4. Comparison between simulation results and prediction values by Geng HY model
表 1 泡沫Au模型的参数表
Table 1. Parameters of foamed gold for shock response simulation
initial thickness of shell d/nm initial outer-radius of shell D0/nm porosity/m atom numbers simulation box size nm 1.3 8 2.146 2 429 272 1777 nm×222 nm×222 nm 1.3 16 3.678 5 671 490 2701 nm×360 nm×360 nm 1.3 20 4.385 7 445 416 2702 nm×450 nm×450 nm 
下载: 导出CSV
-
[1] Hall T, Batani D, Nazarov W, et al. Recent advances in laser-plasma experiments using foams[J]. Laser and Particle Beams, 2002, 20: 303-316. doi: 10.1017/S0263034602202220 [2] Boade R R. Compression of porous copper by shock waves[J]. Journal of Applied Physics, 1968, 39(12): 5693-5702. doi: 10.1063/1.1656034 [3] Rosen M D, Hammer J H. Analytic expressions for optimal inertial-confinement-fusion hohlraum wall density and wall loss[J]. Physical Review E, 2005, 72: 056403. doi: 10.1103/PhysRevE.72.056403 [4] Young P E, Rosen M D, Hammer J H, et al. Demonstration of the density dependence of X-ray flux in a laser-driven hohlraum[J]. Physical Review Letters, 2008, 101: 035001. doi: 10.1103/PhysRevLett.101.035001 [5] Trunin R F, Zhernokletov M V, Simakov G V, et al. Shock compression of highly porous samples of copper, iron, nickel and their equation of state[C]//Shock Compression of Condense Matter. 1998: 83-86. [6] Wu Q, Jing F. Unified thermodynamic equation of state for porous materials in a wide pressure range[J]. Applied Physics Letters, 1995, 67(1): 49-51. doi: 10.1063/1.115488 [7] Geng Huayun, Wu Qiang, Tan Hua, et al. Extension of the Wu-Jing equation of state(EOS) for highly porous materials: Thermoelectron based theoretical model[J]. Journal of Applied Physics, 2002, 92(10): 5924-5929. doi: 10.1063/1.1516619 [8] Jian W R, Li B, Wang L, et al. Shock response of open-cell nanoporous Cu foams: Effects of porosity and specific surface area[J]. Journal of Applied Physics, 2015, 118: 165902. doi: 10.1063/1.4934244 [9] Huang L, Han W Z, An Q, et al. Shock-induced consolidation and spallation of Cu nanopowders[J]. Journal of Applied Physics, 2012, 111: 013508. doi: 10.1063/1.3675174 [10] Zhang L, Ding Y, Lin Z, et al. Demonstration of enhancement of X-ray flux with foam gold compared to solid gold[J]. Nuclear Fusion, 2016, 56: 036006. doi: 10.1088/0029-5515/56/3/036006 [11] Plompton S. Fast parallel algorithms for short-range molecular dynamics[J]. Journal of Computational Physics, 1995, 117: 1-19. doi: 10.1006/jcph.1995.1039 [12] Johnson A. Analytic nearest-neighbor model for fcc metals[J]. Physical Review B, 1988, 37(8): 3924-3931. doi: 10.1103/PhysRevB.37.3924 [13] Luo S N, An Q, Germann T C, et al. Shock-induced spall in solid and liquid Cu at extreme strain rates[J]. Journal of Applied Physics, 2009, 106: 013502. doi: 10.1063/1.3158062 [14] Tan X, Niu G, Li K, et al. Preparation of monolithic foamed gold by seed-mediated growth[J]. Rare Metal Materials and Engineering, 2012, 40(1): 169-172. doi: 10.3969/j.issn.1002-185X.2012.01.038 [15] Olsson P A T. Transverse resonant properties of strained gold nanowires[J]. Journal of Applied Physics, 2010, 108: 034318. doi: 10.1063/1.3460127 [16] Zhakhovskii V V, Inogamov N A, Petrov Y V, et al. Molecular dynamics simulation of femtosecond ablation and spallation with different interatomic potentials[J]. Applied Surface Science, 2009, 255: 9592-9596. doi: 10.1016/j.apsusc.2009.04.082 [17] Yokoo M, Kawai N, Nakamura K G, et al. Ultrahigh-pressure scales for gold and platinum at pressures up to 550 GPa[J]. Physical Review B, 2009, 80: 104114. doi: 10.1103/PhysRevB.80.104114 [18] Grochola G, Russo S P, Snook I K. On fitting a gold embedded atom method potential using the force matching method[J]. The Journal of Chemical Physics, 2005, 123: 204719. doi: 10.1063/1.2124667 [19] Zhou X W, Johnson R A, Wadley H N G. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers[J]. Physical Review B, 2004, 69: 144113. doi: 10.1103/PhysRevB.69.144113 [20] Adams J B, Foiles S M, Wolfer W G. Self-diffusion and impurity diffusion of fcc metals using the five-frequency model and the embedded atom method[J]. J Mater Res, 1988, 4(1): 102-112. [21] Ackland G J, Tichy G, Vitek V, et al. Simple N-body potentials for the noble metals and nickel[J]. Philosophical Magazine A, 1987, 56(6): 735-756. doi: 10.1080/01418618708204485 [22] Liao Y, Xiang M, Zeng X, et al. Molecular dynamics studies of the roles of microstructure and thermal effects in spallation of aluminum[J]. Mechanics of Materials, 2015, 84: 12-27. doi: 10.1016/j.mechmat.2015.01.007 [23] Yokoo M, Kawai N, Nakamura K G, et al. Hugoniot measurement of gold at high pressures of up to 580 GPa[J]. Applied Physics Letters, 2008, 92: 051901. doi: 10.1063/1.2840189 [24] Hodge A M, Biener J, Hayes J R, et al. Scaling equation for yield strength of nanoporous open-cell foams[J]. Acta Materialia, 2007, 55: 1343-1349. doi: 10.1016/j.actamat.2006.09.038 -
下载:
点击查看大图
计量
- 文章访问数: 1180
- HTML全文浏览量: 268
- PDF下载量: 261
- 被引次数: 0
