地脉动环境下反射镜架系统的镜片转角响应计算

陈学前; 沈展鹏; 刘信恩; 胡杰

doi:10.11884/HPLPB201830.170529

地脉动环境下反射镜架系统的镜片转角响应计算

doi: 10.11884/HPLPB201830.170529

陈学前^{1, 2,},
沈展鹏^{1, 2},
刘信恩^{1, 2},
胡杰^{1, 2}

1.
中国工程物理研究院总体工程研究所, 四川绵阳 621999
2.
工程材料与结构冲击振动四川省重点实验室, 四川绵阳 621999

基金项目:

国家重大专项课题资助项目 2016YFB0201005

国家自然科学基金面上项目 11472256

国防基础科研计划资助项目 C1520110002

详细信息

作者简介:
陈学前(1975—)，男，硕士，副研究员，主要从事结构动力学分析与模型V&V研究; chenxq@caep.cn

中图分类号: TN248.1
计量
- 文章访问数: 963
- HTML全文浏览量: 282
- PDF下载量: 125
- 被引次数: 0
出版历程
- 收稿日期: 2017-12-28
- 修回日期: 2018-03-19
- 刊出日期: 2018-07-15

Analysis on rotation angle of mirror in reflector system under ground random vibration

Chen Xueqian^{1, 2
,},
Shen Zhanpeng^{1, 2},
Liu Xin'en^{1, 2},
Hu Jie^{1, 2}

1.
Institute of Systems Engineering, CAEP, Mianyang 621999, China
2.
Shock and Vibration of Engineering Materials and Structures Key Laboratory of Sichuan Province, Mianyang 621999, China

摘要

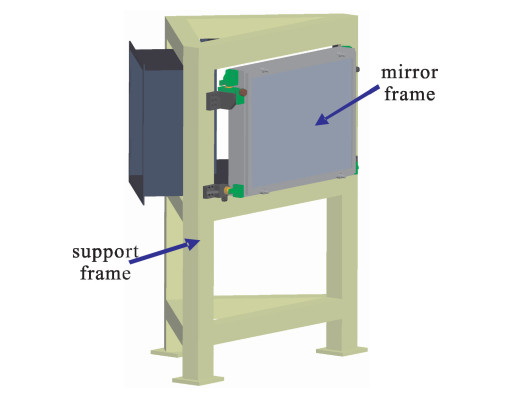
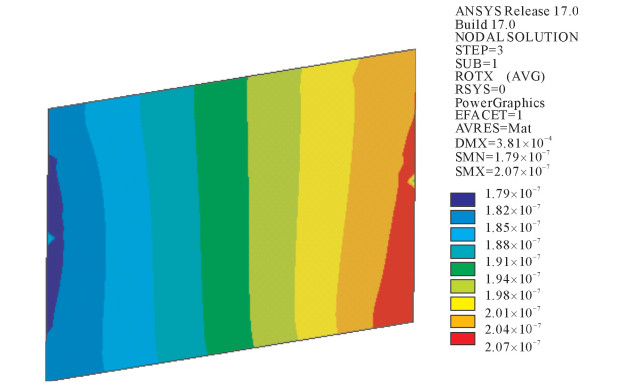
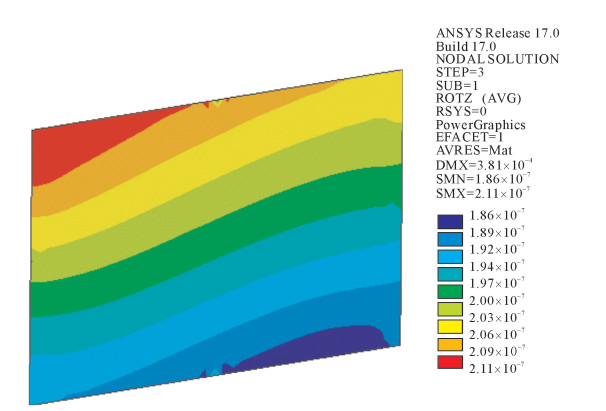
摘要: 反射镜组件是光机装置的重要组成部分，反射镜片的转角稳定性对光路的传输有着直接影响。针对大型光机装置中反射镜架在地脉动随机微振动下的稳定性问题，推导了镜片转角响应均方根值的计算公式。在ANSYS中建立了一个镜架结构的有限元模型，并分析了该镜架系统的模态及结构在地脉动载荷下的微振动响应。根据计算结果分析得到了镜片转角响应均方根值; 提出了工程实际中如何通过有限元分析便捷获得镜片转角响应的另一种工程方法。两种方法所得镜片转角具有较好一致性，说明所采用镜片转角计算分析方法是有效的, 为精密反射镜架的稳定性设计分析提供了有效方法。
- 反射镜架系统 /
- 转角 /
- 有限元分析 /
- 微振动
Abstract: Reflector system is an important part of the laser facility, whose rotation stability has a direct effect on the beam's propagation. Aiming at the stability problem of large-scale precision mirror mount caused by ground random vibration, the formula about the root mean square (RMS) of mirror's rotation angle is deduced. The finite element (FE) model of a reflector system is built in ANSYS, the modal analysis and the micro-vibration calculations are done on the FE model. The RMS rotation angle of the mirror is calculated according to the simulation result. At the same time, another engineering approach to calculate the RMS rotation angle of the mirror is presented by FE simulation. The results of the two approaches are consistent, which shows that the approaches to calculate rotation angle of mirror are effective and reasonable.
- reflector system /
- rotation angle /
- finite element analysis /
- micro-vibration

HTML全文

图 1 反射镜镜面示意图

Figure 1. Sketch map of reflector mirror

下载: 全尺寸图片幻灯片

图 2 反射镜镜架结构系统结构示意图

Figure 2. Sketch map of reflector system

下载: 全尺寸图片幻灯片

图 3 反射镜镜架系统有限元模型

Figure 3. FE model of reflector system

下载: 全尺寸图片幻灯片

图 4 镜架结构1~3阶模态的变形云图

Figure 4. Mode deform contours of the reflector system

下载: 全尺寸图片幻灯片

图 5 镜架结构位移响应云图(mm)

Figure 5. Displacement of the reflector system (mm)

下载: 全尺寸图片幻灯片

图 6 镜片离面位移云图(mm)

Figure 6. Off-surface displacement of the mirror (mm)

下载: 全尺寸图片幻灯片

图 7 镜面绕X轴转角响应(rad)

Figure 7. Rotation angle around X axis of mirror (rad)

下载: 全尺寸图片幻灯片

图 8 镜面绕Z轴转角响应(rad)

Figure 8. Rotation angle around Z axis of mirror (rad)

下载: 全尺寸图片幻灯片

图 9 镜面合转角响应(rad)

Figure 9. Sum rotation angle of mirror (rad)

下载: 全尺寸图片幻灯片

表 1 反射镜架系统的材料参数

Table 1. Material parameters of reflector system

material	elastic modulus /Pa	Poisson’s ratio	density /(kg·m^-3)
45# steel	2×10¹¹	0.3	7850
K9	8×10¹⁰	0.21	2510

下载: 导出CSV

表 2 镜架结构前三阶固有频率的计算结果与试验结果比较

Table 2. Comparison of the first three natural frequencies between simulation and test

mode	test result/Hz	simulation result/Hz	error/%	modal shape
1	20.940	21.471	2.536	X direction whole bend
2	22.261	22.093	-0.755	Y direction whole bend
3	41.822	41.182	-1.530	whole torsion around Z axis

下载: 导出CSV

参考文献(11)

[1]	Moses E I. Introduction to the National Ignition Facility[R]. UCRL-CONF-154962, 2004.
[2]	Trummer J, Foley J, Shaw S. Stability of optical elements in the NIF target area building[C]//Proc of SPIE. 1999, 3492: 363-371.
[3]	冯斌, 周忆, 张军伟, 等. 大型精密镜架地面随机微振动响应分析[J]. 光学精密工程, 2007, 15(3): 356-361. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM200703011.htm Feng Bin, Zhou Yi, Zhang Junwei, et al. Analysis on ground random vibration response of large-scale precision mirror mount. Optics and Precision Engineering, 2007, 15(3): 356-361 https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM200703011.htm
[4]	张军伟, 周忆, 周海, 等. 微振动激励作用下编组站镜架对光束指向的影响[J]. 强激光与粒子束, 2008, 20(5): 779-783. http://www.hplpb.com.cn/article/id/3535 Zhang Junwei, Zhou Yi, Zhou Hai, et al. Influences of switchyard mirror mount on beam direction under micro vibration excitation. High Power Laser and Particle Beams, 2008, 20(5): 779-783 http://www.hplpb.com.cn/article/id/3535
[5]	谢娜, 周海, 张军伟, 等. 大型激光装置光学元件的稳定性设计[J]. 光学精密工程, 2009, 17(10): 2412-2418. https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM200910012.htm Xie Na, Zhou Hai, Zhang Junwei, et al. Stability of optical elements in large laser facilities. Optics and Precision Engineering, 2009, 17(10): 2412-2418 https://www.cnki.com.cn/Article/CJFDTOTAL-GXJM200910012.htm
[6]	陈学前, 杜强, 陈晓娟, 等. 反射镜架系统运动学支撑连接的有限元建模[J]. 强激光与粒子束, 2011, 23(7): 1835-1838. http://www.hplpb.com.cn/article/id/5018 Chen Xueqian, Du Qiang, Chen Xiaojuan, et al. Finite element modeling study on kinematic interface joints of reflector systems. High Power Laser and Particle Beams, 2011, 23(7): 1835-1838 http://www.hplpb.com.cn/article/id/5018
[7]	陈学前, 沈展鹏, 刘信恩. 基于子结构技术的光机装置反射镜组件的稳定性分析[J]. 强激光与粒子束, 2017, 29: 082001. doi: 10.11884/HPLPB201729.170020 Chen Xueqian, Shen Zhanpeng, Liu Xin'en. Stability analysis of reflector module in the laser facility based on sub-structure method. High Power Laser and Particle Beams, 2017, 29: 082001 doi: 10.11884/HPLPB201729.170020
[8]	杜平安, 甘娥忠, 于亚婷. 有限元法——原理、建模及应用[M]. 北京: 国防工业出版社, 2004. Du Pingan, Gan Ezhong, Yu Yating. Finite element method: theory, model building and application. Beijing: National Defense Industry Press, 2004
[9]	庄表中, 梁以德, 张佑启. 结构随机振动[M]. 北京: 国防工业出版社, 1993. Zhuang Biaozhong, Liang Yide, Zhang Youqi. Random vibration of structures. Beijing: National Defense Industry Press, 1993
[10]	Tabatabaie M, Sommer S C. Analysis of soil-structure interaction due to ambient vibration[R]. Livermore: Lawrence Livermore National Laboratory, 1998.
[11]	陈学前, 徐元利. 柔性基础对ICF装置稳定性的影响[J]. 强激光与粒子束, 2011, 23(6): 1569-1573. http://www.hplpb.com.cn/article/id/5292 Chen Xueqian, Xu Yuanli. Studying on the influence of flexible foundation on the stability of ICF facility. High Power Laser and Particle Beams, 2011, 23(6): 1569-1573 http://www.hplpb.com.cn/article/id/5292