Adaptive scanning method for multipactor threshold prediction in microwave devices
-
摘要: 传统的粒子模拟软件在获得微放电阈值时需要进行多次微放电模拟，而且不具备自动功率扫描功能，在不考虑电子运动所产生的自洽场的情况下，提出了一种微波器件微放电阈值功率自适应扫描方法，对同一微波器件中的电磁场只计算一次并重复利用，改变输入功率，获得不同功率下的粒子数目变化的趋势，结合阈值功率判断方法，进而能够快速获得微放电阈值。首先，采用MSAT粒子模拟软件计算单位功率下微波部件中的电磁场分布，接着利用蛙跳法求解粒子运动轨迹，然后结合二次电子发射模型确定出射粒子数目。在微放电模拟过程中对粒子数目曲线进行分析，建立微放电阈值判据方法，根据二分法改变输入功率使得粒子模拟软件在给定初始功率后自动给出微放电阈值。以微波阶梯阻抗变换器与同轴腔体滤波器为研究对象，采用该方法分别计算其微放电阈值并与实验结果进行对比，结果表明，该方法具有准确性。Abstract: Without the power scanning function, the traditional Particle-in-Cell simulation software needs to perform many times in order to achieve multipactor threshold prediction. Therefore, an adaptive scanning method is proposed without considering the self-consistent field generated by electrons. Under the effect of the electromagnetic field distribution calculated by MSAT, the electron motion is tracked and updated with leapfrog algorithm. Secondary electrons are released once electrons reach the boundaries of the simulation region. The criterion for determining multipactor occurrence is established according to the particle number curve via the multipactor simulation. Meanwhile, the power input is adaptively adjusted by the bisection method so that the multipactor threshold can be automatically determined with a given initial power. For verification, multipactor thresholds of stepped impedance transformer and coaxial cavity filters obtained with adaptive-scanning method are compared with experiments. And the simulation results accord well with the experimental data.
-
Key words:
- multipactor threshold /
- Particle-in-Cell /
- bisection method /
- threshold criterion
-
微放电效应[1]是二次电子倍增效应的惯用简称，是发生在航天大功率微波器件中的一种非线性谐振真空放电现象，其物理机制是电子在电磁场作用下加速运动获取能量，与材料表面发生碰撞产生更多二次电子，在这个过程中，电子数目呈指数形式增长。微放电会对航天器产生很大的危害，它是目前空间大功率微波器件的主要失效模式，严重的话，会造成航天器通信系统的损毁。因此，准确预测微放电阈值，改进器件的结构使其避开微放电敏感区域具有非常重要的意义。
目前，微放电阈值分析的方法[2]主要分布在理论和数值模拟两个方面。理论分析方面包括经典理论与统计模型; 数值模拟方面主要有蒙特卡罗方法[3]和粒子模拟方法[4]。与前三种方法相比，基于“第一性原理”方法的粒子模拟[5]在模拟微放电过程中实时更新电磁场，其计算准确度非常高，而且适用于任何复杂器件的微放电阈值计算，但对计算机的性能要求比较高。国际上具有代表性的微放电粒子模拟软件有德国CST公司的CST粒子工作室[6]以及美国MRC公司开发的商用软件MAGIC[7]，国内主流的粒子模拟软件是西安交通大学和西北核技术研究所共同开发的UNIPIC[8]，西安交通大学、东南大学与航天五院西安分院共同开发的MSAT软件[9-10]，但这些粒子模拟软件都不具备自动扫描功能，需要实时观察粒子数目曲线的变化趋势，否则，当输入功率高于阈值功率时，粒子数目急剧增长，导致计算速度越来越慢甚至超过计算机的可计算范围，这无疑会浪费大量时间。国际上关于阈值功率自动扫描方法的报道较少，可供查阅参考的文献不多，具体的阈值判据标准尚不够明确。实际上，在微放电发生或者消失过程中，粒子数目曲线随着时间呈指数增长或下降变化，基于这一特点，通过数值拟合方法建立阈值判据模型，实现微放电阈值功率自动输出，从而大大节省了时间。
考虑到在微放电初始演变阶段，空间中的电子数目较少，电子运动产生的自洽场与微波电场相比可以忽略不计，王洪广等人[11]基于该思想提出了一种微波器件微放电阈值粒子模拟方法，并将该方法计算的微放电阈值结果与CST粒子模拟结果进行对比，证明在计算微放电阈值时可以忽略自洽场。本文以更加高效、准确地计算微波器件微放电阈值为目的，忽略电子运动所产生的电场，提出了一种微放电阈值功率自适应扫描方法。为了验证该方法的准确性，以微波阶梯阻抗变换器与同轴腔体滤波器为研究对象，采用二次电子发射Vaughan模型[12]，利用该方法计算微放电阈值，并将计算结果与实验结果进行比较。
1. 模型
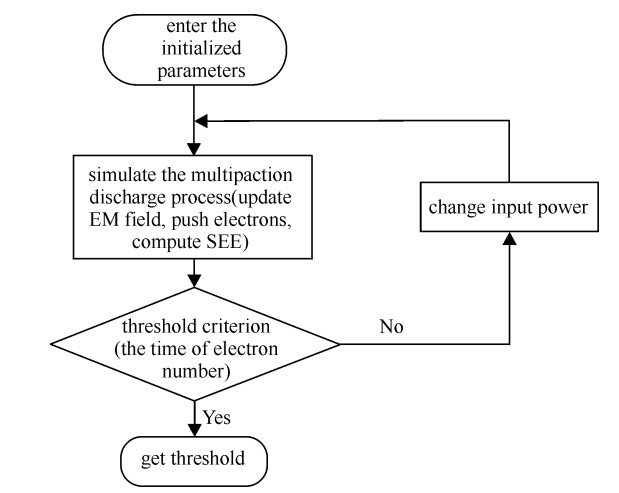
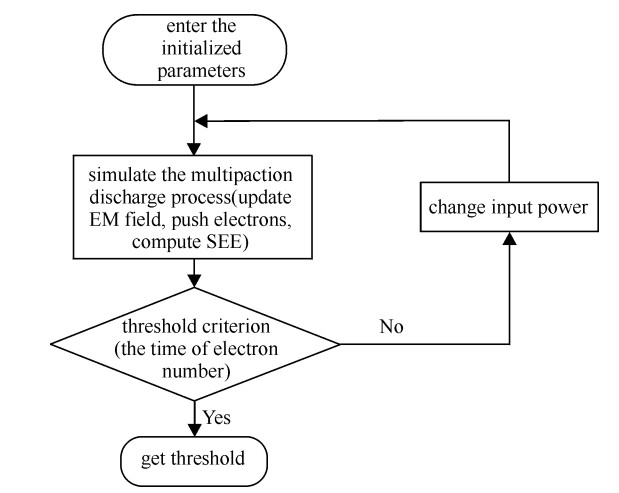
微放电阈值功率自适应扫描方法的主要思想如下：通过重复利用某一功率下的射频电磁场，以二分法方式改变输入功率分别模拟不同功率下的微放电过程，根据阈值判据方法获得器件的微放电阈值功率。以单位输入功率下的电磁场为例，其总体流程如图 1所示。
图 1 微放电阈值功率自适应扫描方法计算流程图Figure 1. Flow diagram of adaptive scanning method for multipactor threshold prediction在仿真微放电过程之前，首先，采用原有粒子模拟软件MSAT计算待求器件中的电磁场，将计算的电磁场结果以频域形式导出，然后输入初始化参数(电磁场频率、已有电磁场功率、初始输入功率与仿真时间步长)，接着进行微放电过程模拟，这一过程主要包括电磁场推进(频域电磁场转换为时域电磁场)、粒子推进(求解牛顿洛伦兹方程获得粒子运动轨迹)以及边界处理(二次电子发射模型)，最后，根据阈值判断方法自动输出微放电阈值。在模拟过程中每隔N个微波周期对粒子数目进行数据拟合并判断是否发生微放电，如果发生微放电(或未发生)，则停止该功率下的微放电过程模拟，同时以二分法方式进行功率修正，并以修改后的功率作为输入功率进行微放电过程模拟，否则继续当前功率下的微放电过程模拟。如此不断循环，直至两次模拟的功率相对误差满足设置精度要求，输出微放电阈值。
1.1 电磁场计算
原有的MSAT软件在模拟微放电过程时实时更新电磁场，即电子运动与电磁场计算之间相互耦合，时间步长受Courant稳定条件限制，而在微放电演变初期，自洽场对计算微放电阈值影响较小可忽略不计，基于这一思想，将求解电磁场模块与电子轨迹计算模块之间去耦合，这无疑可以节省大量计算量，提高计算效率。本文采用MSAT软件计算微波器件中的电磁场分布，目前该软件具有输出频域场以及单位周期内的时域电磁场的功能，考虑到时域电磁场在存储以及读取时计算量非常大而且消耗大量计算机内存，本文选取频域电磁场计算结果，在粒子推进过程中将其转换为时域电磁场[11]。
1.2 阈值判据
在微放电初期，电子相位随机分布，电子在电磁场作用下运动并与器件表面发生碰撞，处于不利相位的电子很快在碰撞中流失，有利相位的电子进入锁相状态，在空间形成一个电荷薄层。此时，平均二次电子发射系数保持常数，粒子数目随时间呈指数变化。因此，判断微放电阈值的方法分为以下两种：一种是依据粒子数目曲线，另外一种是求解平均二次电子发射系数，前者主要是通过观察粒子数目曲线是否呈指数变化趋势，若指数因子大于1，则表明当前功率大于阈值功率，发生微放电。若呈指数衰减，则为不放电; 后者主要是依据平均二次电子发射系数是否大于1来判断微放电是否发生，若大于1，则说明该功率大于阈值功率，否则，当前功率过小。本文基于第一种阈值判断方法，通过对数据拟合确定指数因子实现微放电阈值自适应扫描计算。
在数据拟合过程中，通常采用Rsquare(确定系数)表征数据拟合效果的好坏。在定义该参数之前，需要介绍另外三个物理参数SSR(Sum of squares of the regression)、SST(Total sum of squares)以及SSE(The sum of squares due to error)，其中，SSR代表预测数据与原始数据均值之差的平方和，SST代表原始数据和均值之差的平方和，SSE代表拟合数据和原始数据对应点的误差的平方和，其表达式为
SSR=n∑i=1wi(ˆyi−ˉyi)2 (1) SST=n∑i=1wi(yi−ˉyi)2 (2) 式中：yi代表原始数据; ˆyi代表预测数据; ˉyi代表原始数据均值。
三个参数SSR，SST以及SSE满足以下关系
SST=SSE+SSR (3) Rsquare定义为SSR和SST的比值，即
Rsqquare=SSRSST=SST−SSESST=1−SSESST (4) 从公式(4)可以看出，Rsquare的取值范围为[0, 1]，越接近于1，说明选取的模型对数据拟合得越好。
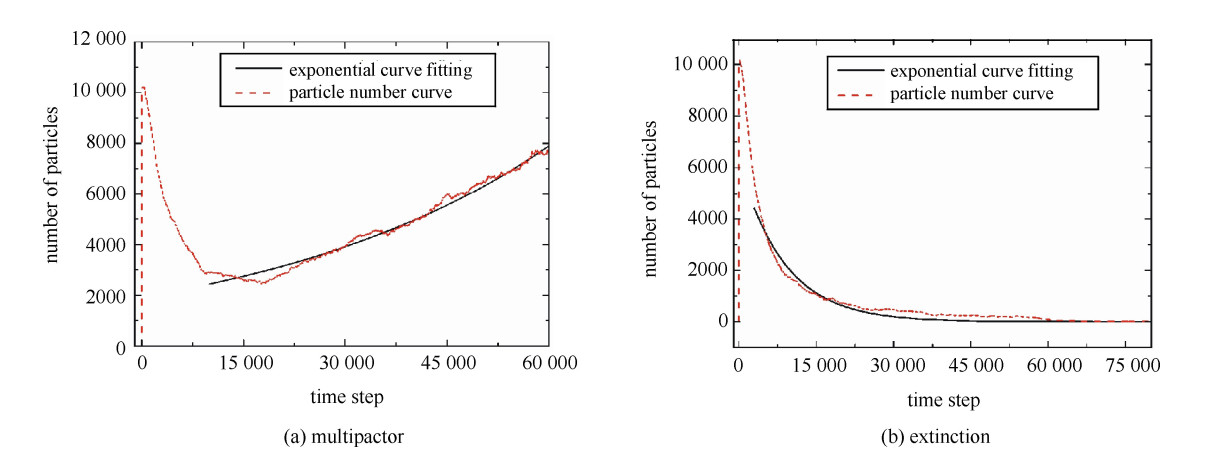
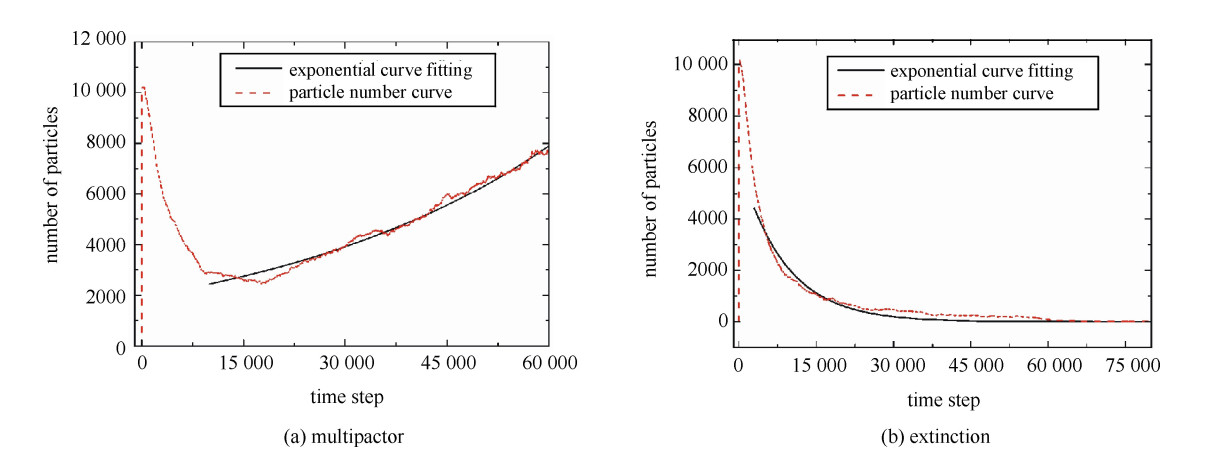
本文选取单指数数学模型分别对发生微放电以及不放电两种情况下的粒子数目曲线进行拟合，图 2(a)为发生微放电时的粒子数目曲线的上升部分的拟合结果对比图，其中拟合参数Rsquare为0.998，图 2(b)为未发生微放电时的粒子数目曲线的下降部分的拟合结果对比图，其中Rsquare为0.996。从图中可以看出，两种情况下的指数拟合曲线与实际粒子数目曲线变化趋势相符，通过判断拟合曲线是否符合指数倍增，可以判断当前功率下器件内是否发生了微放电，进而通过功率修正，模拟下一个功率点下的微放电过程。
1.3 功率扫描
二分法搜索的主要思路是将最低放电功率与最高不放电功率的和的一半作为新的模拟功率，并进行微放电过程模拟，如此不断循环，直至达到设置精度，输出阈值，该方法的优点是简单、便于实现。
在模拟微放电过程之前需要设置初始输入功率，在给定频率与易发生微放电位置的情况下，本文采用平行平板近似下常数k[13-15]或者常数v理论[1, 16]给出微放电阈值估计值，并将此值作为初始功率进行微放电过程模拟，结合阈值判据判断当前功率是否发生微放电，若发生，则改变输入功率，其大小为原有功率的二分之一，并记录上一次模拟微放电的输入功率; 否则，将输入功率设置为原有的2倍，然后进行修改后功率下的微放电过程模拟，以此循环，直至达到给定的设置精度。例如，当软件已达到设置精度时，假设最低放电功率为Pd，最高不放电功率为Pn，则输出阈值(记为Pt)的计算公式如式(2)所示
Pt=(Pd+Pn)/2 (5) 2. 模型验证
应用上述方法分别计算阻抗变换器与同轴腔体滤波器的微放电阈值，并将其与实验结果进行比对，模型中的金属材料采用金属Ag材料，二次电子发射模型选取Vaughan模型。
2.1 阶梯阻抗变换器
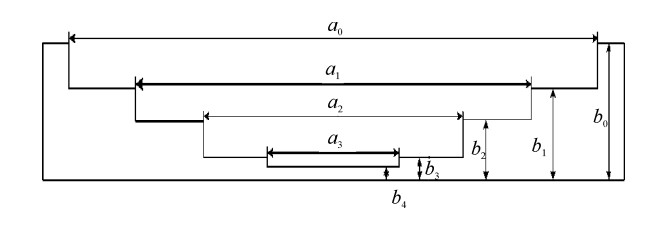
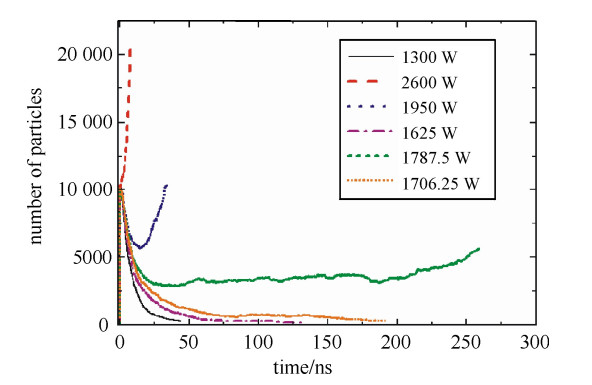
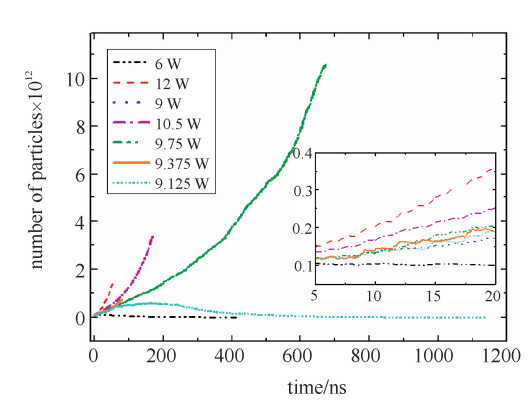
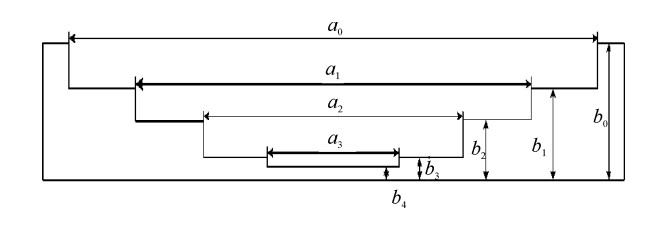
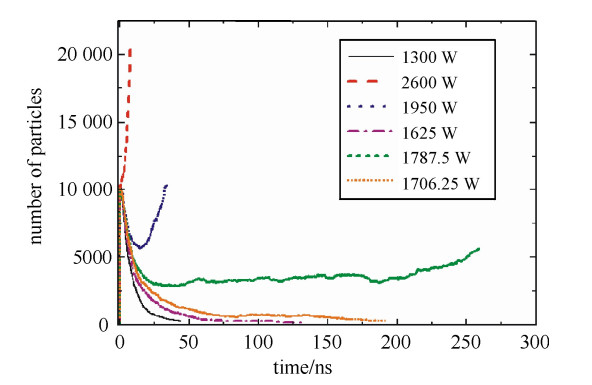
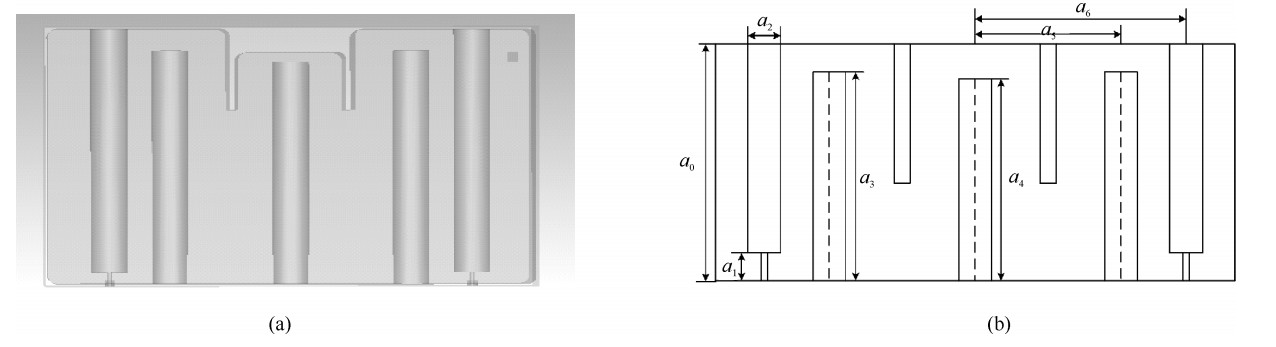
为了验证该方法的正确性，以阶梯阻抗变换器为研究对象，图 3为阶梯阻抗变换器的几何结构图，具体几何结构尺寸列于表 1，选取工作频率为3.85 GHz, 设置起始功率为1300 W，采用上述方法计算其微放电阈值并与实验结果进行比对，其中实验测量阈值功率[18]为1800 W，图 4为微放电阈值功率自适应扫描过程。
表 1 阻抗变换器几何参数(单位：mm)Table 1. Parameters of stepped impedance transformer(unit: mm)a0 a1 a2 a3 b0 218.6 160.16 98.16 50.16 29.08 b1 b2 b3 b4 19 12 3 1 从图 4可以看出，自适应扫描方法计算的阈值功率为1 746.8 W，与实验结果相比，阈值误差为-2.96%，误差较小，达到工程设计要求。
2.2 同轴腔体滤波器
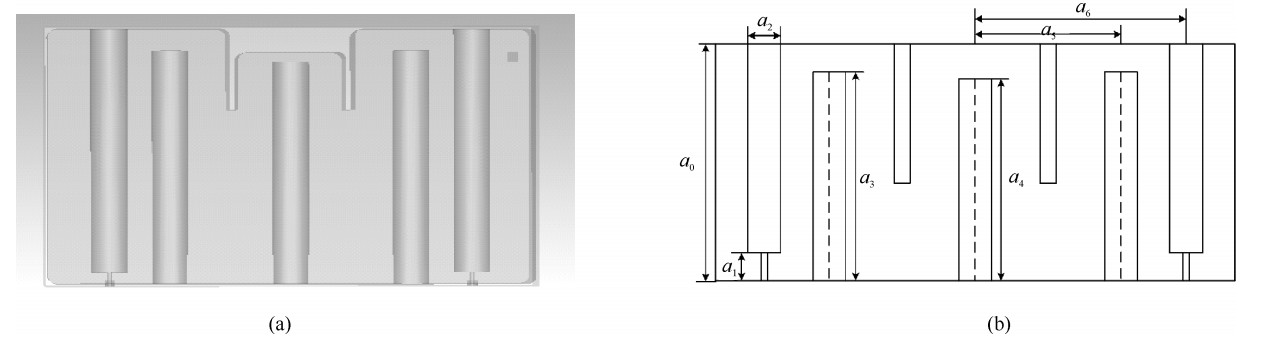
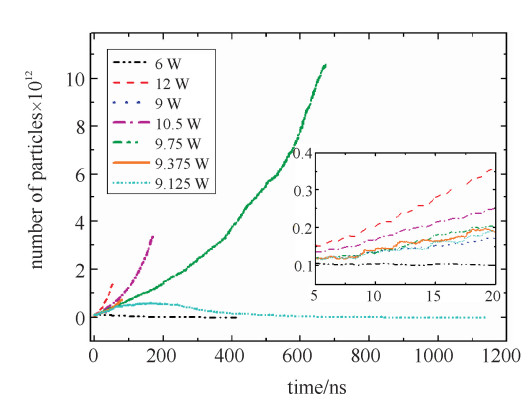
以同轴腔体滤波器为研究对象，图 5为同轴腔体滤波器几何结构示意图，描述该模型的几何参数列于表 2中。设置工作频率为0.34 GHz，起始功率为6 W，给定求解精度3%，其阈值功率扫描结果如图 6所示。
表 2 同轴腔体滤波器几何参数(单位：mm)Table 2. Geometric parameters of coaxial cavity filter(unit: mm)a0 a1 a2 a3 a4 a5 a6 240 5 12 226.3 225 80 127 从图 6中可以看出，采用自适应扫描方法获得的阈值功率为9.281 W，实验测量阈值功率为10 W，两者的阈值相对误差约为-7.19%，满足工程设计要求(3 dB以下)，通过以上结果分析表明，本文提出的微放电阈值功率自适应扫描方法是准确的，能够得到满意的结果，可以用作微波器件微放电阈值功率自适应计算。
3. 结论
本文基于二分法以及数据拟合算法实现了微放电阈值功率自动计算，采用该方法分别模拟了阻抗变换器与同轴腔体滤波器微波器件的微放电过程，并将阈值结果与实验阈值进行对比。结果表明，二者的计算结果几乎一致，本文提出的方法可以用于计算微波器件微放电阈值功率并且可以实现自适应扫描。
-
图 1 微放电阈值功率自适应扫描方法计算流程图
Figure 1. Flow diagram of adaptive scanning method for multipactor threshold prediction
表 1 阻抗变换器几何参数(单位：mm)
Table 1. Parameters of stepped impedance transformer(unit: mm)
a0 a1 a2 a3 b0 218.6 160.16 98.16 50.16 29.08 b1 b2 b3 b4 19 12 3 1 
下载: 导出CSV
表 2 同轴腔体滤波器几何参数(单位：mm)
Table 2. Geometric parameters of coaxial cavity filter(unit: mm)
a0 a1 a2 a3 a4 a5 a6 240 5 12 226.3 225 80 127
下载: 导出CSV
-
[1] Vaughan J R M. Multipactor[J]. IEEE Trans Electron Devices, 1988, 35 (7): 1172-1180. doi: 10.1109/16.3387 [2] Kishek R A, Lau Y Y, Ang L K, et al. Multipactor discharge on metals and dielectrics: Historical review and recent theories[J]. Physics of Plasmas, 1998, 5(5): 2120-2126. doi: 10.1063/1.872883 [3] Ang L K, Lau Y Y, Kishek R, et al. Power deposited on a dielectric by multipactor[J]. IEEE Transactions on Plasma Science, 1998, 26 (3): 290-295. doi: 10.1109/27.700756 [4] Nieter C, Stoltz P H, Roark C, et al. Modeling of multipacting in RF structures Using VORPAL[C]//AIP Conf Proc, 2010. [5] Birdsall C K, Langdon A B. Plasma physics via computer simulation[M]. New York: Taylor & Francis, 2004: 1-400. [6] Computer Simulation Technology (CST) Center 2012 Framingham M A http://www.cst.com[2015-10-21]. [7] Goplen B, Ludeking L, Smith D, et al. User-configurable MAGIC for electromagnetic PIC calculations[J]. Computer Physics Communications, 1995, 87 (1/2): 54-86. [8] 李永东, 王洪广, 刘纯亮, 等. 高功率微波器件2.5维通用粒子模拟软件——尤普[J]. 强激光与粒子束, 2009, 21(12): 1866-1870. http://www.hplpb.com.cn/article/id/4307Li Yongdong, Wang Hongguang, Liu Chunliang, et al. 2.5-dimensional electromagnetic particle-in-cell code—UNIPIC for high power microwave simulations. High Power Laser and Particle Beams, 2009, 21 (12): 1866-1870 http://www.hplpb.com.cn/article/id/4307 [9] Li Y, Cui W Z, Wang H G. Simulation investigation of multipactor in metal components for space application with an improved secondary emission model[J]. Physics of Plasmas, 2015, 22 (5): 1172-2126. [10] You J W, Wang H G, Zhang J F, et al. Accurate numerical method for multipactor analysis in microwave devices[J]. IEEE Transactions on Electron Devices, 2014, 61 (5): 1546-1552. doi: 10.1109/TED.2014.2313027 [11] 王洪广, 翟永贵, 李记肖, 等. 基于频域电磁场的微波器件微放电阈值快速粒子模拟[J]. 物理学报, 2016, 65(23): 275-281. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201623035.htmWang Hongguang, Zhai Yonggui, Li Jixiao, et al. Fast particle-in-cell simulation method of calculating the multipactor thresholds of microwave devices based on their frequency-domain EM field solutions. Acta Physica Sinica, 2016, 65 (23): 275-281 https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201623035.htm [12] Vaughan J R M. New formula for secondary emission yield[J]. IEEE Transactions on Electron Devices, 1989, 36(9): 1963-1967. doi: 10.1109/16.34278 [13] Hatch A J, Williams H B. The secondary electron resonance mechanism of low-pressure high-frequency gas breakdown[J]. Journal of Applied Physics, 1954, 25 (4): 417-423. doi: 10.1063/1.1721656 [14] Hatch A J, Williams H B. Multipacting modes of high-frequency gaseous breakdown[J]. Physical Review, 1958, 112(3): 681-685. doi: 10.1103/PhysRev.112.681 [15] Woo R, Ishimaru A. A similarity principle for multipacting discharges[J]. Journal of Applied Physics, 1967, 38 (13): 5240-5244. doi: 10.1063/1.1709307 [16] Wachowski H. Breakdown in waveguides due to the multipactor effect[R]. TDR-269-(9990)-5, 1964. [17] 李永东, 闫杨娇, 林舒, 等. 微波器件微放电阈值计算的快速单粒子蒙特卡罗方法[J]. 物理学报, 2014, 63(4): 317-321. https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201404045.htmLi Yongdong, Yan Yangjiao, Lin Shu, et al. A fast single particle Monte-Carlo method of computing the breakdown threshold of multipactor in microwave device. Acta Physica Sinica, 2014, 63(4): 317-321 https://www.cnki.com.cn/Article/CJFDTOTAL-WLXB201404045.htm [18] Li Y, Cui W Z, Wang H G. Simulation investigation of multipactor in metal components for space application with an improved secondary emission model[J]. Physics of Plasmas, 2015, 22(5): 1172-2126. 期刊类型引用(3)
1. 任三孩，古松，谭谦，叶新，方进勇. 电子诱发波导微放电实验研究. 强激光与粒子束. 2023(03): 115-120 . 
本站查看2. 李韵，封国宝，谢贵柏，苗光辉，李小军，崔万照，贺永宁. 大功率铁磁性微波部件微放电演变机理与抑制. 强激光与粒子束. 2022(06): 33-38 . 本站查看3. 林舒，翟永贵，张磊，王洪广，王瑞，李永东，刘纯亮. 粒子模拟在空间大功率微波器件微放电效应研究中的应用. 真空电子技术. 2019(06): 55-61 . 百度学术其他类型引用(1)
-
下载:
点击查看大图
计量
- 文章访问数: 1160
- HTML全文浏览量: 330
- PDF下载量: 135
- 被引次数: 4
